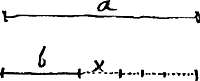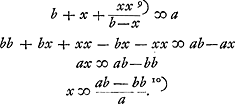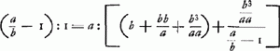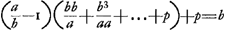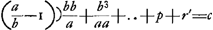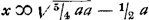Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651

[p. 53]

X.¹⁾
[1646].

Theorema. 1.²⁾
Si sint quotlibet numeri vel lineae in proportione geometrica, numero qui oritur ex divisione primae per secundam, multata unitate, et sic multiplicata cum summa omnium, exceptâ primâ, additoque ad hoc productum ultima; quod orietur erit ipsa prima proportionalium.

Sint numeri proportionales a. b. bb/a. b³/aa. divisâ primâ per secundam oritur a/b.

1) Dans la première partie de cette pièce, jusqu'au ‘Problema’ Huygens se propose évidemment de démontrer bien rigoureusement la formule pour la somme d'une suite géométrique à nombre infini de termes. Dans la seconde partie se trouvent des applications de cette formule.

2) La numération est de Huygens.

[p. 54]

2.
Consequitur hinc denominatorem proportionis demptâ unitate, habere eam proportionem ad unitatem, quam habet prima proportionalium ad summam reliquarum una cum ultima per denominatorem³⁾ divisâ, et permutando.

3.
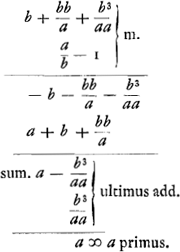
Sequitur quoque quamcunque proportionalium divisam per denominatorem proportionis multatum unitate, aequalem esse descendentibus omnibus in infinitum proportionalibus.

Sint enim proportionales a et b; et b divisa per a/b - 1, sit c; si ergo reliquae proportionales in eadem proportione a ad b sint inaequales lineae c, erunt majores vel minores, sit ergo primum c major proportionalibus, et sit differentia d; inveniatur



igitur proportionalis quâ divisa per a/b - 1. fiat r′⁴⁾ minor differentia d, ergo haec una cum omnibus proportionalibus à b deorsum usque ad ipsam aequalis erit c, ex ante demonstratis.⁵⁾ sit autem haec summa Br⁶⁾, ergo utriusque ablatâ AB;⁷⁾ deberet pars r′⁴⁾, quae extra AB est aequalis esse d, tota autem r′⁴⁾ minor est d.⁸⁾

3) Intercalez: ‘demptâ unitate’; alors on obtient la proportion correcte:



.

4) Le texte a r, que nous avons remplacé par r′ pour éviter un double emploi de cette lettre.

5) Soit, en effet, p le ‘proportionalis’ en question. On a alors par le 1^er théorème: , donc:(divisant par

6) Voir la figure.

7) AB représente la somme des ‘proportionels’ bb/a, b³/aa etc. jusqu'à l'infini.

4) Le texte a r, que nous avons remplacé par r′ pour éviter un double emploi de cette lettre.

4) Le texte a r, que nous avons remplacé par r′ pour éviter un double emploi de cette lettre.

8) Huygens supprime, évidemment comme superflue, la réduction à l'absurde du ‘secundum’ c'est-à-dire, de la supposition: ‘c minor proportionalibus.’

[p. 55]

Problema.
Data linea a et alia b, invenire tertiam lineam, ut b et ipsa, cum omnibus proportionalibus, quae sunt in continua proportione in infinitum ut b ad ipsam, simul aequales sint lineae a datae.

Sit linea quaesita ∞ x. Ergo denominator proportionis erit b/x. Quia itaque pono



x etiam pro ultima, (omnes enim reliquae una cum ultima divisa b/x - 1 semper aequales sunt sibi invicem, quamobrem non refert quot proportionales constituas,) debet ideo

⁹⁾¹⁰⁾

9) Ce terme représente la somme des ‘proportionels’ qui viennent après l'x. Il a été obtenu, comme une annotation à part l'indique, au moyen de la formule: x : (b/x - 1) qui résulte du 3^me théorème.

10) Suit la construction et encore deux autres problèmes que voici, qui sont résolus de la même façon:
‘Data linea a, invenire lineam aliam, ita ut omnes continuae proportionales, in proportione quam habet a ad ipsam, una cum ipsa, proportionem habeant ad a, quam habet a ad ipsam.’ (Huygens trouve: ‘ Id est si a secetur media et ultima proportione major pars erit ∞ x’)
‘Datis duabus lineis a et b invenire partem quam occupaturae sunt caeterae omnes proportionales continuatae in eadem proportione in infinitum.’ (Huygens trouve facilement: ).
Après cela on lit encore:
‘Consequentia ex antedictis haec sunt.
1. Differentiam inter primam et secundam proportionalium esse ad primam, ut secunda ad omnes proportionales, excepta prima.
2. Denominatorem proportionis dempta unitate habere eam proportionem ad unitatem, quam major proportionalium ad omnes reliquas; et permutatim.
Ut si sint proportionales in tripla proportione, erit maxima dupla reliquarum omnium.’