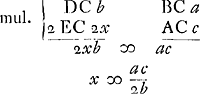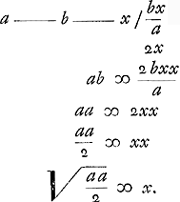8.
Datum triangulum per punctum intra ipsum datum bifariam secare.Ga naar voetnoot13)
|
-
voetnoot1)
- Cette pièce contient la solution de huit problèmes de planimétrie. Il est difficile de décider si elle a été composée sous l'influence du premier précepteur Stampioen de Jonge ou bien sous celle de van Schooten. Plusieurs problèmes ont beaucoup de ressemblance avec ceux qu'on rencontre dans les ‘cent questions géométriques avec leurs solutions’ par Sybrandt Hansz. de Harlingen, maître arithméticien à Amsterdam, ouvrage recommandé par Stampioen de Jonge dans la pièce No. 5 (p. 5 du T. I) à l'étude de Huygens avec l'injonction d'en résoudre les problèmes tant arithmétiquement, par le calcul, que géométriquement, par la règle et le compas. Par contre il semble bien probable que le troisième problème a été composé par Huygens à propos des remarques et exemples de van Schooten, qu'on trouve aux pages 300 et 301 du manuscrit dont l'aperçu constitue notre pièce No. I (voir le § 8 de cette pièce). Quoique, naturellement, l'idée d'élucider par un exemple le passage en question de la ‘Géométrie’ de Descartes ait pu venir indépendamment à Huygens comme à van Schooten.
-
voetnoot2)
- Jusqu'au numéro 6 inclus, la numération est de Huygens.
-
voetnoot4)
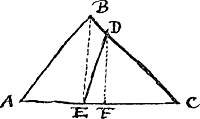
- Au 89ième problème, Sybrandt Hansz., dans l'ouvrage cité dans la note 2 de la pièce No. 5 (p. 5 du Tome I), apprend à inscrire un carré dans un triangle donné; et cette même question se trouve résolue algébriquement à la page 12 du manuscrit de van Schooten. (Voir la pièce No. I du volume présent). La construction, à laquelle Sybrandt Hansz. arrive, est moins simple et moins élégante que celle de Huygens, qui va suivre, du problème analogue; quoique cette dernière se laisse déduire sans difficulté de la formule algèbrique qui la précède, il semble plus probable qu'elle ait été obtenue directement au moyen de considérations géométriques faciles à deviner, mais que Huygens ne donne pas.
-
voetnoot5)
- Lisez IB, c'est-à-dire la hauteur du triangle.
-
voetnoot6)
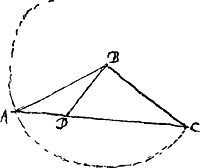
- C'est ce problème et sa solution, reproduits par van Schooten dans la première édition de 1649 de ses ‘Commentarii in Geometriam Renati Des Cartes’, ouvrage cité dans la note 1 de la Lettre No. 150, p. 218 du T. I, qui constituent la première oeuvre imprimée de Huygens. Tandis que dans la seconde édition, parue en 1659, de l'ouvrage de van Schooten, Christiaan Huygens est mentionné plusieurs fois, on ne rencontre son nom dans la première édition qu'à un seul endroit (pp. 203-205) qui débute comme il suit: ‘Alterum exemplum, quod hic afferendum duxi,’ [voir pour le premier exemple et pour le passage de la ‘Géométrie’ qu'il s'agit d'élucider le § 8 de la pièce No. I] ‘desumpsi ex inventis Nobilissimi & praeclari Juvenis D. Christiani Hugenii, quibus sibi jam pridem apud Doctos tantam paravit laudem atque admirationem, ut non nisi magna quaeque ab eo expectanda esse affirmare non veriti fuerint.’ Suit alors, sous une rédaction un peu modifiée, le problème de notre texte et sa solution, après quoi van Schooten ajoute: ‘Quia igitur hic utrinque eaedem reperiuntur quantitates, & adimpletis omnibus conditionibus nulla ampliùs inveniri potest aequatio, quâ innotescat utraque incognita quantitas x &
y: liquet eas ad libitum sumi posse, atque Problema propositum esse Theorema. Defectus itaque duarum in hâc quaestione conditionum ad determinandum punctum E, ostendit, illud ubique extra diametrum, intra circulum cadere posse, & locum ejus esse ad superficiem Circuli. Id quoque facilè demonstrari potest.’ etc.
-
voetnoot7)
- Au 48e problème Sybrandt Hansz. demande que le gnomon en question ait une aire donnée. Sous cette forme plus générale le problème a été repris par Huygens le 31 déc. 1651, à la page 177 du manuscrit mentionné dans la note 1 de la pièce No. I. Comme cette solution ne présente rien de remarquable nous ne la reproduirons pas.
-
voetnoot8)
- Le 77e problème de Sybrandt Hansz demande de partager le triangle, sous les mêmes conditions, en trois parties égales. De plus le problème est un cas particulier du 8e, que l'on retrouve dans le 92e problème de Sybrandt Hansz.
-
voetnoot10)
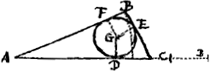
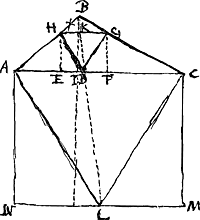
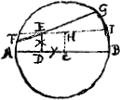
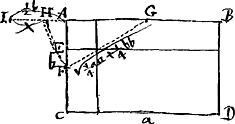
- Il suffit, en effet, pour le voir, d'identifier les points A, B, C, D de la figure du texte avec les points F, C, I, E de celle du troisième problème. Alors ▭ ADC = ▭ FEI = aa - xx - yy, □ BD = □ CE = xx + yy.
-
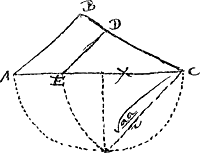
voetnoot13)
- C'est le 92e problème de Sybrandt Hansz. Au lieu d'une solution on ne trouve que deux figures biffées, difficilement déchiffrables et qui en tout cas ne représentent pas la construction complète. Le problème analogue, pour un point extérieur, est résolu de deux manières différentes dans le manuscrit de van Schooten traité dans la pièce No. I, et Huygens a ajouté à la seconde construction une démonstration (voir le problème 25 à la p. 14 de la pièce No. I). Dans l'ouvrage ‘Exercitationum mathematicarum’ etc. de 1657 (voir la note 3 de la Lettre No. 128, p. 184 du T. I) van Schooten a publié (p. 107-110 du Livre I) la solution du problème plus général: ‘Triangulum ABC secare in data ratione rectâ EFG, procedente ex vel per datum punctum E. extra vel intra triangulum ABC.’
|


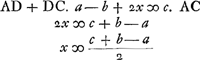
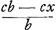 sive HE.
sive HE.
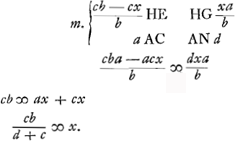
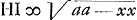 et
et 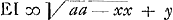 et
et 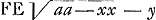 , ergo rectangulum FEI fiet si multiplicavero
, ergo rectangulum FEI fiet si multiplicavero

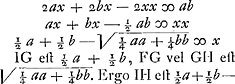
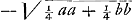 , sive x.
, sive x.