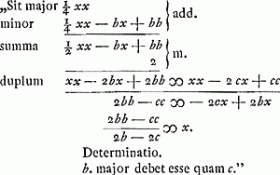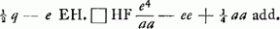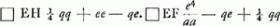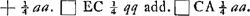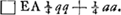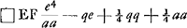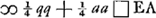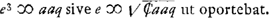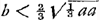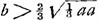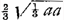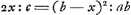Oeuvres complètes. Tome XI. Travaux mathématiques 1645-1651
(1908)–Christiaan Huygens–
[pagina 7]
| |
I.
§ 1. Les pages 1-23 contiennent des problèmes d'algèbre et de géométrie, dont la solution, qui n'y manque nulle part, dépend de la résolution d'une équation du premier degré à une seule inconnue. Voici le premier de ces problèmes: ‘Invenire duos numeros, quorum summa sit 8, et differentia 2.’ A la page 18 on trouve la question suivante: ‘Sunt duae turres AB, CD quorum altitudo utriusque cognoscitur AB valere a vel 60 pedes, CD autem b vel 52 pedes. Quaeritur locus E, ê quo si ponantur scalae pertingant ad summitatem utriusque turris B et D. Cum distantia earundem turrium AC sit c vel 64 pedes.’ La distance AE du point cherché, au pied de la première tour, est égalée à x et on trouve | |
[pagina 8]
| |
Demonstratio. quoniam proport.les sunt dupla AC,’ sans achever ni la ‘Compositio’ ni la ‘Demonstratio.’ C'est la seule annotationGa naar voetnoot4) de sa main que l'on trouve dans cette partie du manuscrit, et encore est-elle, d'après l'écriture, d'une date bien postérieure à la composition du manuscrit.
§ 2. Viennent ensuite, aux pages 24-58, les 37 premières questions du premier livre de l'ouvrage bien connu de DiophanteGa naar voetnoot5), accompagnées de solutions algébriques sous une forme presque moderne. Les 22 premières mènent, comme celles des pages précédentes 1-23, à des équations du premier degré à une inconnue.Ga naar voetnoot6) Trois inconnues sont introduites dans les solutions des questions 23 et 24. Ensuite dans les questions 25-28 le nombre des inconnues excède celui des équations, ce qui fait remarquer par van Schooten: ‘quaestionem non esse omnino determinatam, sed infinitas habere solutiones, atque idcirco unam ex illis radicibus’ [ce sont les trois inconnues x, y, z] ‘ad libitum esse sumendam, ut hic z,’ etc. Ajoutons que, à propos de la ‘Quaestio XXVI’, Huygens a annoté ‘Diophantus habet 150, 92, 120, 114’, ce qui en effet ne s'accorde pas avec la solution indéterminée donnée par van Schooten, lequel avait pris l'énoncé du problème dans un sens qui n'était pas dans l'intention de Diophante. Enfin, après la 29ième question qui conduit à l'équation 25 xx ∞ 200 x, la ‘Quaestio XXX’ donne lieu à l'équation quadratique complète xx ∞ 20 x-96, dont les racines sont calculées d'après l'algorithme suivant: 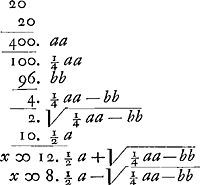 Ici les chiffres sont de van Schooten; mais dans les lettres a et b on reconnaît la main de Christiaan, qui les a ajoutées en guise d'explication (Comparez la pièce No. II), ainsi que cela arrive encore à quelques autres endroits du manuscrit, comme aussi dans la 31iême question. Vient ensuite la ‘Quaestio XXXII’ dont la solution, qui d'ailleurs ne présente aucune difficulté, puisqu'elle conduit facilement à une équation du premier degré, est écrite de la main de Huygens, | |
[pagina 9]
| |
tandis que, au contraire, dans les questions 33-37, l'énoncé est de la main de Huygens et la solution de celle de van Schooten. § 3. Les pages 59-74 débutent par la solution de la question ‘Propositum quadratum dividere in duos quadratos,’ la huitième du Livre II de l'ouvrage mentionné de Diophante. Pour y parvenir, on pose xx et 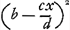 pour les deux carrés dont la somme doit égaler bb, à propos de quoi Huygens remarque: ‘Idem aliter fieri poterat ponendo pro uno numero bb - 2bx + xx, pro altero ccxx et repertum fuisset in fine aequationis pour les deux carrés dont la somme doit égaler bb, à propos de quoi Huygens remarque: ‘Idem aliter fieri poterat ponendo pro uno numero bb - 2bx + xx, pro altero ccxx et repertum fuisset in fine aequationis 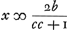 .’ Après, viennent les solutions des problèmes 10, 11, 12 et 13 du même livre II de Diophante, augmentées de celles des quatre suivantes: 1. ‘Duos numeros quadratos invenire, quorum summa sit numerus quadratus;’ 2. ‘Duos numeros invenire quorum tam summa quam excessus sit numerus quadratus’; 3. ‘Datis duobus cubis, invenire duos alios cubos, quorum differentia aequet summam datorum; 4. ‘Datis duobis cubis invenire duos alios cubos, quorum differentia aequet differentiam datorum.’Ga naar voetnoot7) Ensuite les pages 69-73, dont les deux premières ont été empruntées au Livre III des .’ Après, viennent les solutions des problèmes 10, 11, 12 et 13 du même livre II de Diophante, augmentées de celles des quatre suivantes: 1. ‘Duos numeros quadratos invenire, quorum summa sit numerus quadratus;’ 2. ‘Duos numeros invenire quorum tam summa quam excessus sit numerus quadratus’; 3. ‘Datis duobus cubis, invenire duos alios cubos, quorum differentia aequet summam datorum; 4. ‘Datis duobis cubis invenire duos alios cubos, quorum differentia aequet differentiam datorum.’Ga naar voetnoot7) Ensuite les pages 69-73, dont les deux premières ont été empruntées au Livre III des
| |
[pagina 10]
| |
‘Zeteticorum’ de VièteGa naar voetnoot8) (Zet. 7 et 8), traitent la construction d'un triangle à côtés et à aire rationaux; enfin la page 74 est de nouveau occupée par un problème menant à une équation ordinaire du premier degré.
§ 4. Les pages 75-102 contiennent, avec les règles pour la sommation, la multiplication, etc. des nombres irrationaux, celles pour trouver la racine quadratique ou cubique d'un binôme comme 7 + √48 ou 10 + √108 dans le cas où cette racine peut être réduite à la forme même d'un tel binômeGa naar voetnoot9). Elles se terminent par quelques problèmes qui mènent à des expressions irrationnelles, comme par exemple celui de trouver le côté d'un octogone régulier quand le rayon du cercle circonscrit a été donné.
§ 5. Aux pages 103-130 qui constituent dans leur ensemble un petit traité sur les équations algébriques supérieures au second degré, on retrouve presque textuellement le Livre III de la Géométrie de Descartes à commençer par le paragraphe: ‘De la nature des Equations’ et à finir par celui qui est intitulé: ‘Que tous les problesmes solides se peuuent reduire à ces deux constructions’ (pp. 444-473 du T. VI de l'édition d'Adam et Tannery)Ga naar voetnoot10); seulement, van Schooten a ajouté à ce dernier paragraphe encore cinq nouveaux exemples, plus | |
[pagina 11]
| |
simples que ceux qui sont traités par Descartes. Voici les deux premiers: ‘Datam
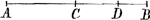 rectam lineam AB secare in extremâ ac mediâ ratione duplicata, hoc est ut AB sit ad AC ut AC ad CD, et ita CD ad DB.’ ‘In triangulo rectangulo ABC, demissa ex angulo recto B perpendiculari BD in lat. oppositum AC, detur segmentum AD ∞ a, et area trianguli DBC ∞ bb. Invenire triangulum. Partout dans ces exemples l'analyse algébrique est suivie de la construction au moyen de la parabole et du cercle. Dans le cinquième: ‘E serie quatuor continue proportionalium, datâ primâ majore a, et differentiâ secundae et quartae b, invenire secundam et tertiam,’ la solution est de la main de Huygens. Elle est comme il suit: ‘Sit secunda x et fiat, ut prima (a) ad secundam (x) ita secunda (x) ad tertiam (xx/a); ut secunda (x) ad tertiam (xx/a) ita tertia (xx/a) ad quartam (x3/aa). Ergo x - x3/aa ∞ b. aax - x3 ∞ aab. x3 ∞ aax - aab. assumpta a pro unitate fiet. 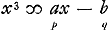 . .
‘Determinatio: b non potest major dari quam 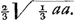 Ga naar voetnoot11) alias enim a non potest esse major, quatuor proportionalium.’ Ga naar voetnoot11) alias enim a non potest esse major, quatuor proportionalium.’
De plus, à la dernière des pages 125-130, qui traitent la règle de Cardan, on trouve à côté des mots ‘Denique, si habeatur x3 ∞ + px - q,’ etc. un signe de renvoi qui conduit à la note suivante de Huygens: ‘Cum habetur x3 ∞ px - q ad inveniendam radicem scribatur y3 ∞ py+q. Ex qua aequatione inventâ radice y per regulam Cardani, cognoscetur quoque x namque erit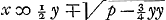 . .
Cujus regulae ortus ut intelligatur sciendum est, cum utrique aequationis parti x3 ∞ px-q, additur y3 tum alteram quidem dividi posse per x+y, fierique xx - xy + yy; altera vero px + y3 - q per eandem x + y divideretur si foret py∞y3-q; essetque quotiens p. nam px+py esset hoc casu altera aequationis pars, | |
[pagina 12]
| |
quam quidem sic dividi constat per x + y. Adaequando igitur py ∞ y3 - q. fit y3 ∞ py + q cujus aequationis radix y inveniri potest per Cardani regulam. Et quum ex divisione utriusque partis aequationis supradictae per x + y, oriatur xx - xy + yy ∞ p. Erit xx ∞ xy - yy + p. Et 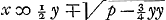 .’ .’
‘Et hac quodem ratione in Arithmeticis quaestionibus radicem invenire licet, melius quam Geometrica descriptione. nam per hanc quomodo investigabitur Radicem x3 ∞ 7 x - 6 esse 2 vel 1, quod per jam explicatam methodum invenitur ponendo y3 ∞ 7x + 6Ga naar voetnoot12). fitque y ∞ 3.’Ga naar voetnoot13) Enfin au pied de la même page 130 on lit de la main de Huygens: ‘Finis prioris partis scriptorum Schotenij;’ après quoi Huygens fait suivre à la page 131: ‘De his vide appendicem cubicarum aequationuni quam Fr. Schotenius adjunxit libello de Organica Conicorum Sectionum descriptione.’Ga naar voetnoot14)
§ 6. Arrivé à la fin de la première partie du manuscrit de van Schooten, nous devons remarquer que dans la seconde partie, qui occupe les pages 282-348, plusieurs des pièces qui la constituent doivent être lues dans l'ordre inverse de la paginationGa naar voetnoot15), c'est-à-dire en commençant p.e. par la page de droite. Et cet ordre inverse est sans doute, en substance, l'ordre chronologique. Nous commençons donc par les dernières pages 312-348 où l'on trouve les solutions de 25 problèmes divers, arithmétiques et géométriques, qui, à part quelques exceptions peu importantes, dépendent de la résolution d'équations quadratiques. Dans tous les problèmes géométriquesGa naar voetnoot16) l'analyse algébrique est accompagnée de la construction qui en résulte. Voici quelques-uns de ces problèmes: 2.Ga naar voetnoot17) ‘Rhombo dato ABCD, ductaque diagonali BD. Ex puncto A rectam | |
[pagina 13]
| |
lineam ducere AEFG, ita ut pars EF intercepta inter diag. BD et latus DC habeat ad totam rationam datam’. G se trouve sur le côté BC prolongé. 12. ‘Datum trapezium’ [ici un quadrilatère quelconque] ‘ABCD ita secare lineis EF, FG, GH et EH lateribus undique parallelis et ab iisdem aequali intervallo distantibusque; ita ut pars abcissa aequalis sit dato spatio.’ 13. ‘Data base trianguli AC, angulo verticis D, et aggregato laterum circa angulum verticis, invenire triangulum.’ 24. ‘Dato parallelogrammo ABCD et producto latere BC indefinite versus G,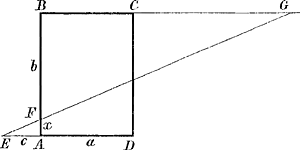 ex puncto E sumpto in AD producto rectam lineam ducere EFG, quae faciat triangulum FBG aequale parallelogrammo ABCD.’ À ce dernier problème Huygens a annoté en tête: ‘Pappus Lib. 7. propos. 164’.Ga naar voetnoot18) Plus bas, où van Schooten, après avoir obtenu la solution sous la forme 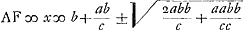 , ajoute la remarque ‘Maior radix , ajoute la remarque ‘Maior radix
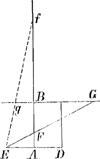 in hac quaestione inutilis est’, Huygens évidemment n'accepte pas cette assertion et la réfute par la figure que voici, tracée de sa main. Enfin on trouve de la main de Huygens sur la page suivante l'annotation qui suit et qui constitue une analyse algébrique, fondée sur l'équation quadratique 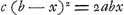 , à laquelle van Schooten a réduit le problème; analyse, qui aurait pu conduire facilement à une construction simple, que Huygens toutefois n'a pas pris la peine d'indiquer expressément: , à laquelle van Schooten a réduit le problème; analyse, qui aurait pu conduire facilement à une construction simple, que Huygens toutefois n'a pas pris la peine d'indiquer expressément:
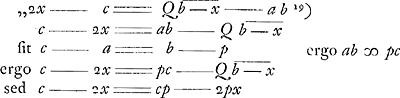 | |
[pagina 14]
| |
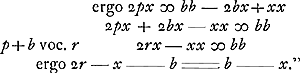 Cette annotation est datée au 20 aoust 1653. Vient ensuite le problème 25, que 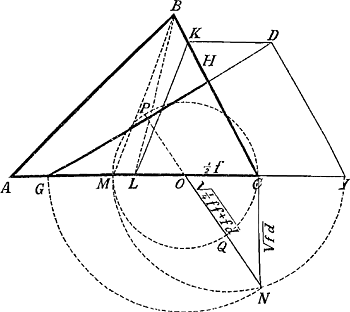 voiçi, écrit comme les autres de la main de van Schooten: ‘Dato triangulo ABC, et extra ipsum puncto D. Ex D rectam lineam ducere, quae bifarium secet triangulum.’ De ce problème van Schooten donne deux solutions différentes, dont nous reproduisons la plus fimple et la plus élégante puisque Huygens y a ajouté, en décembre 1651, la ‘demonstratio’, que l'on trouvera à la fin. ‘AB ∞ a, AC ∞ b, BC ∞ c, CI ∞ d, ID ∞ e, GC ∞ x. Ergo GI erit x+d. Iam propter triangula similia GHC, GDI, fiat ut GI (x+d) ad ID (e) ita GC (x) ad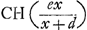 .
Rectang. sub AC, BC. bc, fit ergo .
Rectang. sub AC, BC. bc, fit ergo 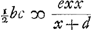 rectang. sub GC, CH. rectang. sub GC, CH.
½bcx + ½ bcd ∞ exx xx ∞ bc/2e x + bc/2e d. Resoluatur fractio bc/2e in proportionem, dicendo ut 2 ID (2e) ad AC (b) ita BC (c) ad bc/2e, quod vocetur f, hoc est fiat ut 2 ID ad AC, sive ut semissis huius ad semissem illius id est ut ID vel CK ad ½ AC vel CL, ita BC ad quartam CM ∞ f. xx ∞ fx+fd;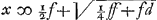 . .
Demonstratio. die ult.à 1651. Semidiametro OM vel OC describatur circulus PMQC, et producatur NO ad circumf. Est igitur ▭ PNQ hoc est ▭ CGM aequale qu. CN tangentis, hoc est ▭o MCI; ergo erit GM ad MC ut CI ad | |
[pagina 15]
| |
CG, per 16. 6.Ga naar voetnoot20) et componendo GC ad MC ut GI ad GC, hoc est ut DI vel KC ad HC. ergo ▭ sub GC, HC aequale ▭o sub MC, KC. sed hoc aequale est ▭ BC, LC, quoniam ex constr. est: BC ad MC ut KC ad LC. ergo quoque ▭ sub GC, HC aeq. ▭ sub BC, LC, quare per 15.6 erit et triang. GCH aequ. triango. BCL sive dimidio triangulo ABC; quod erat dem.’ Ajoutons que la dernière page 349 contient une table des ‘Numeri Graecorum’, écrite par Huygens, dont voici les dernières lignes:  § 7. Aux pp. 306-311 on rencontre six problèmes, qui mènent à des lieux géométriques. En voici le premier: A datis duobus punctis A et B, inflectere duas 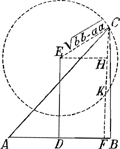 rectas lineas AC, CB ita ut quae ab iis fiunt quadrataGa naar voetnoot21) habeant ad triangulum ACB datam rationem. Ratio data sit ut DE quater sumpta ad DB.’ Posant AD ∞ DB ∞ a, DE ∞ b, DF ∞ x, CF ∞ y, la relation yy ∞ 2by - aa - xx est obtenue, à quoi Huygens fait suivre: ‘et 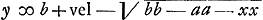 .’ Vient ensuite la ‘Constructio’, c'est-à-dire la description du cercle, lieu du point C, ayant E pour centre et dont le rayon égale .’ Vient ensuite la ‘Constructio’, c'est-à-dire la description du cercle, lieu du point C, ayant E pour centre et dont le rayon égale 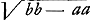 . Ici Huygens ajoute: ‘posito enim pro x DF ad lubitum, erit etiam EH ∞ x; quare HGa naar voetnoot22) erit . Ici Huygens ajoute: ‘posito enim pro x DF ad lubitum, erit etiam EH ∞ x; quare HGa naar voetnoot22) erit 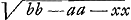 , et tota , et tota 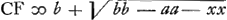 , vel , vel 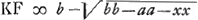 . Haec autem determinatio est, quod b debet major dari quam a.’ . Haec autem determinatio est, quod b debet major dari quam a.’
En tête du second, du cinquième et du sixième des problèmes mentionnés Huygens a écrit: ‘Ex Pappo’. On les retrouve en effet dans le septième Livre de l'ouvrage de Pappus mentionné dans la note 18, là où Pappus, aux pages 162 et 163, donne l'aperçu bien connu des ‘lieux plans’ d'Apollonius.Ga naar voetnoot23) De plus, à propos | |
[pagina 16]
| |
du cinquième problème: ‘A datis duobus punctis A et B inflectere rectas duas lineas AD, DB in ratione data AC ad CB’, Huygens remarque: ‘Si oporteat quadrata linearum AD, DB esse in data ratione, rursus locus puncti D erit circumferentia circuli, nam ubicunque sumatur in eê punctum D, habebunt quadrata AD, DB inter se eandem rationem, nimirum duplicatam rationis datae AC ad CB’Ga naar voetnoot24).
§ 8. Les pp. 300-305 contiennent la discussion, élucidée par des exemples, des cas où les questions géométriques amènent des équations algébriques soit identiques, soit fausses, soit insuffisantes en nombre. On y trouve, pp. 300-301, avec la suscription ‘Locus ad superficiem’, deux problèmes qui ont dû servir sans doute à expliquer le passage de la ‘Géométrie’ de Descartes, où on lit, (p. 407 du Tome VI de l'édition d'Adam et Tannery): ‘Et s'il manque deux conditions à la détermination de ce point, le lieu où il se trouve est une superficie, laquelle peut estre tout de mesme ou plate ou spherique ou plus composée.’ Le premier de ces problèmes: ‘Dato triangulo aequilatero ABC in eoque ducta perpendiculari BD: oportet invenire punctum E intra triangulum, à quo si ducantur tres perpendiculares EF, EG et EH in singula latera, ut summa ipsarum aequetur perpendiculari BD.’ a été reproduit par van Schooten dans ses Commentaires sur la ‘Geometria’, (voir la note 9) p. 201 de l'édition de 1649; l'autre: ‘Dato circulo circa A centrum, invenire punctum B extra centrum, per quod si ducantur duae rectae lineae CD, EF normaliter invicem secantes in B, quadrata segmentorum CB, BD, EB et BF simul sumpta quadrato diametri sint aequalia,’ lequel, de même, conduit à une équation identique, y a été remplacé par un exemple imaginé par le jeune Huygens. On le trouvera au § 3 de la pièce No. III.
§ 9. Les pages 296-299 se retrouvent, sous une forme plus achevée et un peu modifiée, aux pages 207-212 de l'édition seconde (de 1659) de la ‘Geometria’ par van Schooten, sous le titre: ‘De locis solidis sive conicarum sectionum proprietatibus.’ On y trouve la déduction des équations de la parabole, de l'hyperbole et de l'ellipse (et encore dans le manuscrit celle du cercle anti-parallèle), considérées comme sections du cône scalène à base circulaire. | |
[pagina 17]
| |
Dans le cas de la parabole van Schooten, après avoir obtenu l'équation sous la forme: My ∞ xx, ajoute: ‘Quod demonstrat, si fiat ut rectangulum sub AB, BC ad quad. AC ita EB ad quartam M, quae latus rectum vocetur. Porro manifestum
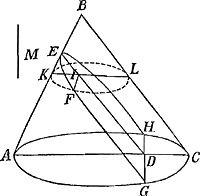 hinc est, lineam M multiplicatam per EI facere semper productum aequale quadrato ordinatae FI. Quae est 11 prop. 1 libri Apollonii Conicorum.’Ga naar voetnoot25) A propos de quoi Huygens ajoute à la date du 1 Sept. 1653. ‘Demonstratio. Ratio BE ad M est eadem quae rectanguli AB, BC ad quad. AC hoc est, eadem compositae ex ratione BC ad CA, et BA ad CA. Est autem ut BC ad CA ita EI ad IK, et ut BA ad CA ita BE ad IL; ergo ratio BE ad M componitur ex ratione EI ad IK, et BE ad IL sed ratio BE ad M itidem componitur ex ratione BE ad IL et IL ad M, ergo ratio composita ex ratione EI ad IK et BE ad IL eadem est compositae ex BE ad IL et IL ad M. quare sublata communi proportione quae est BE ad IL, erit eadem ratio EI ad IK quae IL ad M. ideoque rectangulum sub IK, IL h.e. quadratum IF aequale ▭o EI, M.’
§ 10. Les pages 288-295 contiennent, sous le titre ‘De inveniendis tangentibus linearum curvarum modo Domni Descartes’, l'application de la méthode, exposée par Descartes au second livre de sa ‘Géométrie’ (voir les pp. 413-424 du T. VI de l'édition d'Adam et Tannery), à la parabole, l'ellipse, l'hyperbole, la conchoïde et à l'ovale de Descartes. Les applications à l'ellipse et à l'ovale de Descartes se retrouvent dans la ‘Géométrie’ au lieu cité; celles à la parabole, l'hyperbole et la conchoïde dans les Commentaires de van Schooten, pp. 216-222 de l'édition de 1649 de la ‘Geometria’. Dans le manuscrit, l'application à l'hyperbole est de l'écriture de Huygens, mais elle correspond exactement à celle à l'ellipse, qui est de la main de van Schooten et qui elle-même ne diffère pas sensiblement de celle qu'on trouve dans la ‘Géométrie’ de DescartesGa naar voetnoot26). Pour cette raison nous croyons pouvoir la passer. Une autre annotation de Huygens se rapporte à la construction, donnée par | |
[pagina 18]
| |
Descartes sans démonstration, de la normale à la conchoïdeGa naar voetnoot27) (voir les p. 423-424 de l'éd. citée de la ‘Géométrie’). 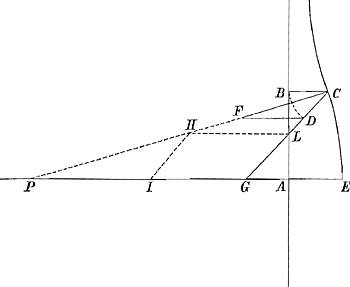 Par l'analyse, qui a été reproduite dans les ‘Commentarii’ p. 219-222 de l'édition de 1649, van Schooten arrive à la formule 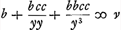 ∞ v, où v = AP; b = GA; c = LC; y = BC. Il s'agit donc de démontrer que, par la construction qui suit et qui est celle de Descartes, on a en effet ∞ v, où v = AP; b = GA; c = LC; y = BC. Il s'agit donc de démontrer que, par la construction qui suit et qui est celle de Descartes, on a en effet 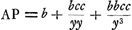 . .
‘Constructio.’Ga naar voetnoot28) ‘Sumatur CD aequalis CB, ducaturque DF parallela cum AP et aequalis ipsi GL, ducaturque FC, hanc dico secare conchoidem in C ad angulos rectos.’ Demonsratio. Propter triangula similia si fiat ut BC ∞ y ad AG ∞ b, ita LC ∞ c ad LG ∞ bc/y, eaque nominetur g, et erit gc/y. idem ac bcc/yy. ad resolutionem autem hujus fractionis, fiat ut y vel CD ad g vel DF, ita c vel CL ad gc/y vel bcc/yy, lineam LH sive GI eaque nominetur h: eritque bbcc/yyy idem ac hb/y, ad resolutionem autem hujus fractionis, fiat ut y vel BC ad b vel AG sive (quod idem est propter triangula similia BCL et AGL) ut CL ad LG vel ipsi aequalem HI, ita h vel LH ad bh/y vel bbcc/yyy lineam IP, propter ∆la similia CLH et HIP.’ ‘Sumatur igitur CD aequalis ipsi CB, ductaque DF aequali GL et parallela | |
[pagina 19]
| |
cum AP, tum FC quaesitâ et constat fieri PI ∞ bbcc/y3 GI ∞ bcc/yy et AG ∞ b, et AP vel v ∞Ga naar voetnoot29) bcc/yy + bbcc/y3 quod erat demonstrandum.’ § 11. Aux pages 284-287, sous le titre: ‘De Maximis et Minimis sive Ratio inveniendi casum determinationis in Problemate determinato juxta Methodum Domni de Fermat,’ la méthode de Fermat, publiée en 1644, dans le sixième volume de l'ouvrage de Hérigone cité dans la note 4 de la lettre No. 139 (p. 203 du T. I), est appliquée à quatre problèmes, dont deux: ‘Invenire maximum rectangulum contentum sub duobus segmentis datae rectae lineae’; ‘Invenire maximum rectangulum contentum sub media et differentia extremarum trium proportionalium’ se retrouvent chez Hérigone, p. 59 et p. 60 de l'ouvrage cité. Voici les autres: ‘Datis positione duabus rectis lineis annuentibus AB, CB et puncto D intra angulum ab iis comprehensum. Oportet per D rectam lineam ducere ADC, quae faciat triangulum ACB minimum omnium sic factorum’; ‘Data parabola CE 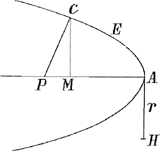 et puncto in eius axe P. Oportet ex P rectam lineam ducere PC quae sit minima omnium quae ex puncto P ad parabolam duci possunt.’ Pour résoudre ce dernier problème, van Schooten, après avoir posé AH (latus rectum) ∞ r, AP ∞ a, AM ∞ x, trouve facilement □ PC ∞ aa-2ax+rx+xx. Puis il refait le même calcul pour la valeur AM ∞ x + y, trouvant ┚ PC ∞ aa - 2ax + rx + xx-2ay +ry + 2xy+ yy. Égalant ces deux valeurs de ┚ PC et divisant par y, il obtient l'équation - 2a + r + 2x + y ∞ 0, et, enfin, posant y ∞ 0, la solution donne x ∞ a - ½ rGa naar voetnoot30), après quoi Huygens a ajouté plus tard: ‘Ad hunc modum in Conchoide quoque et reliquis lineis curvis tangentes ad data puncta duci possunt. nam si datâ AP invenire possum AM et MC, etiam harum unâ datâ noscitur AP, ex eadem aequatione.’
§ 12. Enfin les pages 282 et 283 contiennent, sous le titre: ‘De Inveniendis | |
[pagina 20]
| |
tangentibus Linearum curvarum secundum methodum Domni Fermat,’ l'application de cette méthode à la parabole et à l'ellipse, tout comme chez Hérigone, p.65-68 de l'ouvrage cité dans le paragraphe précédent; mais avec d'autres notations.
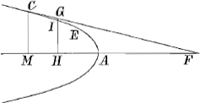 Voici, pour faire comprendre l'annotation de Huygens qui va suivre, la solution pour la parabole telle qu'on la trouve dans le manuscrit: ‘Data parabola CE in dato puncto C invenire tangentem parabolam.’ ‘Sit illa tangens CF. Et esto MA ∞ a, MF ∞ x. Per 20 prop. lib. 1mi Conicorum Apollonii. Quadratum CM ad quadratum IH eam habet rationem quam MA ad HA. Habet autem quad. CM ad quad. IH majorem rationem quam ad quad. GH per 8. 5.Ga naar voetnoot31) Ut autem □ CM ad □ GH ita est □ FM ad □ HF. Itaque habebit MA ad HA maiorem proportionem quam □ MF ad □ HF.’  A quoi Huygens a fait suivre plus tard mais à une date inconnue: ‘Schotenius inventionem hujus regulae non percepit, quae est hujusmodi.Ga naar voetnoot33) Recta CF supponenda est secare parabolam in G, indeque ductam perpendicularem GH. datis jam MA ∞ a, et MH ∞ y, oportet invenire quanta sit MF ∞ x. Invenitur xx ∞ 2ax - ay. β, quadrata aequatio quum MH ∞ y certam lineam denotat. verum si MH non sit major nihilo, impune deletur - ay fitque xx ∞ 2ax et x ∞ 2a.’ |
|


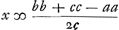 ; après quoi Huygens a ajouté: ‘sit bb + cc - aa ∞ qq
; après quoi Huygens a ajouté: ‘sit bb + cc - aa ∞ qq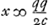 . Compositio. Inveniatur linea Q cujus quadratum aequetur □ AC + □ DC.
. Compositio. Inveniatur linea Q cujus quadratum aequetur □ AC + □ DC.