Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 288]

N^o 2222.
Ph. de la Hire à Christiaan Huygens.
1680.
Appendice II au No. 2219.

La pièce se trouve à Leiden, coll. Huygens¹⁾.

Demonstration de Monsieur De La Hire.

Par les 3 points F,A,B, qui sont communs a l'hyperbole et à la parabole soit descrit le cercle FMAB, qui rencontrera la parabole^a) au mesme point E ou elle rencontre l'hyperbole ou bien qui la rencontrera en quelque autre point e. S'il la rencontre au point E, la propos. est evidente par ce qui a estè demontrè^b) des rencontres de la parabole et du cercle: mais s'il la rencontre en quelqu'autre point e.

Ayant menè AB,Fe, qui se rencontrent en quelque point P, ces lignes seront antiparalleles à l'axe de la parabole, par ce qui a estè demontrè des rencontres de

1) Elle est entièrement écrite de la main de Chr. Huygens.

a) il falloit parler en general de quelque section coniq. que ce soit [Chr. Huygens]³⁾.

3) Le renvoia) s'applique également au mot hyperbole souligné dans le manuscrit, de même que le mot parabole.

b) ces paroles sont superflues. [Chr. Huygens]

[p. 289]

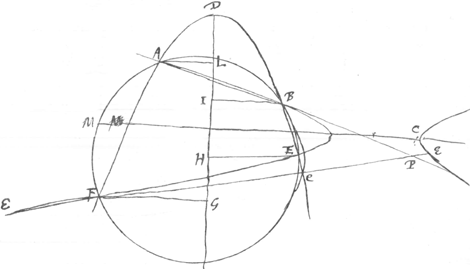
la parabole et du cercle. Mais puisque l'axe de la parabole est parallele à l'un de ceux de l'hyperbole ou de l'ellipse ces mesmes lignes seront antiparalleles a l'axe de l'hyperbole.

C'est pourquoy si l'on mene deux touchantes à l'Ellipse a une hyperbole ou aux sections opposees²⁾, qui soient paralleles a ces deux lignes AB, FE, elles se rencontreront necessairement sur l'un des axes, puis qu'elles font des angles egaux avec luy, c'est pourquoy elles seront egales et leurs quarrez egaux entre eux.

Mais a cause du cercle le rectangle AP, PB, est egal au rectangle EP, Pe.

^c) S'il est possible, que la ligne Fe rencontre l'hyperbole ou l'Ellipse en quelque autre point E que F: par la proprieté des sections coniques le rectangle AP, PB sera au rectangle EP, PF, comme les quarrez des touchantes qui sont paralleles à AB et à Fe. les quelles sont egales comme il a estè demontrè cy dessus. donc le rectangle AP, PB sera egal au rectangle EP, PF, il seroit donc possible de descrire un cercle ABFE²⁾ different^d) du cercle ABeF ce qui est absurd, car ils auroient chacun les trois points ABF communs.

Il faut donc necessairement que le cercle FMAB rencontre l'Ellipse ou l'hyperbole au mesme point E ou la rencontre la parabole, et par les proprietez des rencontres de la parabole et du cercle la proposition est evidente.

2) Ces mots sont soulignés par Huygens.

c) Il faudroit avoir montrè qu'elle doit la rencontrer en quelqu'autre point que F. Elle peut toucher l'hyperbole. alors F, E, coincident, et le cercle menè par AB touchera la droite Fe en F. donc il ne peut passer un autre cercle par AB Fe, puisque par ABF il n'en peut passer qu'un. [Chr. Huygens]

2) Ces mots sont soulignés par Huygens.

d) C'est peut estre le mesme. Il faut donc montrer que ce ne peut estre le mesme cercle parce qu'il rencontreroit la droite Fe en 3 points. [Chr. Huygens].

3) Le renvoia) s'applique également au mot hyperbole souligné dans le manuscrit, de même que le mot parabole.