Oeuvres complètes. Tome VIII. Correspondance 1676-1684

[p. 80]

N^o 2128.
Monforte à Christiaan Huygens.
juin 1678.

La pièce se trouve à Leiden, coll. Huygens.

^a) Ex datis quatuor lineis trapezium efficere aream datae aequalem habens.

Datae quatuor lineae vocentur a, b, c, d. Area data cui aequalis esse debet area Trapezii t, diagonios BD y. Ex his ad aequationem, quae diagonion explicat, unde determinationem area[e] trapezii accipit, sic devenimus.

Semissis summae laterum trianguli ABD est c + d + y/2 differentiae inter hanc semissen, et singula latera, d + y - c/2. c + y - d/2. c + d - y/2 quae mutuo ductu efficiunt 2ccdd + 2ccyy - y⁴ - d⁴ + 2dd - c⁴/16 quadratura areae trianguli ABD eàdemque ratione quadratura areae alterius trianguli BDC invenitur 2aabb + 2bbyy - y⁴ - b⁴ + 2aa - a⁴/16 Atqui trapezium divisum est in haec duo triangula, erit, (suppositis brevitatis gratia loco 2ccdd - d⁴ - c⁴, h, et loco 2cc + 2dd, k nec non pro 2aabb - b⁴ - a⁴, s et pro 2bb + 2aa, g) aequatio inter + t et √s + gyy - y4/16 + √h + kyy - y4 / 16. Sublataque asymmetria fit^b)

y^4 ∞ 2ghyy + 2fh

- 2gf - ff

+ 32gtt - hh

+ 32ktt - 32htt

+ 2kf + 32ftt

- 2kh + 256t^4

_____

kk + gg + 64tt - 2kg

a) Rec. 21 Jun. 1678 [Chr. Huygens].

b) t - √∞√ tunc y⁴ tollitur et fit aequatio quae est hic.[Chr. Huygens].

[p. 81]

Si vero speciebus sequentes valores tribuantur, a 13, b 5, c 20, d 16, fiet h aequalis ipsi f, ac aequatio in hanc breviorem mutabitur

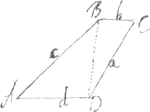
y⁴ ∞ 32gttyy - 256t⁴ 32ktt + 64ftt/kk + gg + 64tt - 2kg ubi si pro g, k et f projuxta valores restituantur, et pro t, assumatur 126, totaque aequatio eveletur, ac juxta dictas regulas corrigatur expliceturque, emerget 144 pro yy, et diagonios BD erit 12, Hinc si supra diagonon BD, utrumque triangulum BAD, BCD, constitui intelligantur, ita ut trapezium ABCD efficiant, quaesito satisfactum est^c)1).

c) Determinationem maximi non addidit quam praecipue quaerebam. [Chr. Huygens]²).

2 Le livre E des Adversaria montre, pp. 44 à 50, que Huygens, en 1675, s'est occupé du problème qu'il paraît avoir proposé à Monforte. On y trouve, entre autres, une solution de Römer (methodus Romeri), et une de lui-même (methodus nostra) avec la détermination du maximum et le théorème suivant: Polygonum circulo inscriptum maximum est omnium quae iisdem lateribus, quocumque ordine nexis, continentur.

1) En bas de la deuxième page du manuscrit Chr. Huygens nota: Il Sig. Monforte che e nobile per nascita, e dottissimo nelle Matematiche.

2 Le livre E des Adversaria montre, pp. 44 à 50, que Huygens, en 1675, s'est occupé du problème qu'il paraît avoir proposé à Monforte. On y trouve, entre autres, une solution de Römer (methodus Romeri), et une de lui-même (methodus nostra) avec la détermination du maximum et le théorème suivant: Polygonum circulo inscriptum maximum est omnium quae iisdem lateribus, quocumque ordine nexis, continentur.