Oeuvres complètes. Tome VI. Correspondance 1666-1669
(1895)–Christiaan Huygens–
[pagina 546]
| |||||||||||||||||||
Problema Problematum.Datam quamlibet aequationem secundo gradu altiorem, dummodo infra dicendam praeparationem admittat, ad ipsum secundum gradum infinitis modis depremere. | |||||||||||||||||||
Fons Inuentionis.Bene quidem Cartesius omnia geometriae problemata, siue aequationes omnes, cum ad magnitudines reuocantur, circuli, et curuarum, quas geometricas vocat, linearum, gradatim magis ac magis, pro aequationis natura compositarum intersectione soluere nos edocuit. Non absimilem methodum haberemus si quis nobis artem traderet quaslibet aequationes sola rectarum linearum dictas curuas secatntium opera resoluendi. Sed quoniam nulla alia Cartesiana, vel hujus vltima, si extaret, methodi ratio reddi potest, nisi quod regulares curuae lineae certas quasdam proprietates in se continent, proposita aequationis natura correspondentes, quo efficitur vt omnes soluendis problematibus idonea sint, ac quaelibet aequatio pro numero dimensionum ex quibus composita est peculiarem, vt soluatur, curuam lineam requirat, necessarias, et ejus naturae conuenientes proprietates in se complectentem. Hinc alius, et quidem longè simplicissimus vltro se se offert regulares curuas lineas considerandi modus, si nimirum ad instituendam, et perficiendam problematum analysim curuarum linearum proprietatibus sic vtamur, vt postea ipsas vel describere vel a rectis lineis, circulisue secare necesse non sit. Nam hac ratione idem quod alij praestabimus eodem quippe fundamento vtentes ad plana reuocabitur geometrica quaelibet effectio, atque per vnicam regulam infinitas diversorum graduum aequationes resoluemus et itaque | |||||||||||||||||||
Regula generalis Pro aequationum depressione ad 2um gradum.Supponatur curua quaelibet linea regularis (hoc est cujus omnia puncta ad alicujus rectae lineae puncta certam quandam relationem habeant, quae per eandem aequationem exprimi possit). Ita tamen vt ipsa circuli atque rectae lineae beneficio describi queat; et sit ejus vertex, mGa naar voetnoot1), axis mk, latus rectum siue pa- | |||||||||||||||||||
[pagina *27]
| |||||||||||||||||||
 | |||||||||||||||||||
[pagina 547]
| |||||||||||||||||||
rameter, si quam habeat, ml. Tum puncto q in axi ad arbitrium assumpto infra verticem, factum esto Δlum rectangulum ghv, simile alteri cuidam Δlo rectangulo, cujus latera sint r, y, p, et punctum h in assumpta curua existat. Sit autem y incognita litera alicujus aequationis, quam ad secundum gradum deprimere volumus, sed quam hic vt cognitam consideramus, et qv vocetur v. Deinde ex similitudine Δlorum ryp, et qhv, atque ex valore □ti applicatae hv siat aequatio ab incognita v denominata, quae ad 2um gradum ascendet, et in cujus coefficientibus literae y immiscebitur. Postea litera y induat valorem in assumptae aequationis inuolucri, latentem, quod facile fiet si in dicta aequatione, ab incognita v denominata, litera y, quae in ea reperitur, toties per se ipsam multiplicetur, quo vsque ascendat ad altissimum gradum, quem in deprimenda aequatione occupat. Demum si pro illo altissimo gradu reliquam deprimendae aequationis partem, ipsi altissimo gradui aequalem ponamus, et extracta bimensae aequationis ab incognita v denominatae radice in locum v, ejus inventum valorem subrogemus, atque ex aliqua assumptae curuae lineae proprietate, per quam rectae lineae, in eadem curua se se secantes certam quandam inter se relationem induunt, aequatio condatur, et a suis surdis liberetur, erit illa quam quaerimus, nam ab incognita y denominabitur. Quod si deprimenda aequatio duos tantum terminos habeat, vt accidit in Mesolabij inuentione, enata per traditam regulam aequatio non altius quam ad 3um gradum assurget, dummodo parabolâ, quae post circulum curuarum linearum simplicissima est, vti velimus, vt sequentibus patebit. Et quoniam dictae operationes per arbitrariam punctorum in axi, et cujusdam rectae axim secantis, vel ipsi parallelae assumptionem absolui queunt, ac canonica electae curuae descriptio circuli, atque rectae lineae beneficio peragi potest, vt supposuimus, sequitur necessaria ad propositi problematis constructionem puncta in electa curua existentia per planorum doctrinam semper inueniri posse, nec postea opus esse curuam illam describere, quae ideo tantum supposita est, vt ejus proprietatibus vteremur ad instituendam aequationem, quae soluendo problemati nostro inseruiret. Atque cum nulla imaginari possit curua linea, ex infinita illarum, quas regulares nominaui multitudine, quae non sit ad hunc effectum vtilis, simul methodum habemus propositum problema infinitis modis resoluendi. Haec Regula omnium, quae in Mathesi excogitari queunt, perfectissima videtur, nam cunctorum quot quot occurrunt problematum solutiones ea sola complexa est. Verum quum plurimae aequationes certa quadam preparatione indigent, antequam huic Regulae feliciter applicentur, qua de re postea nobis erit disserendum. Nunc vero hujus Regulae auxilio inter duas datas rectas lineas quot libet medias proportionales per planorum doctrinam inuenire, siue Mesolabum per rectas lineas, atque circulos construere doceamus. | |||||||||||||||||||
Problema 1um.Inter duas datas rectas lineas quotlibet medias proportionales per planorum doctrinam inuenire, siue Mesolabum per rectas lineas, atque circulos construere. | |||||||||||||||||||
[pagina 548]
| |||||||||||||||||||
Datum.Dentur duae rectae lineae b quidem major, et c minor, inter quas inueniendae sint quotlibet mediae continuè proportionales. | |||||||||||||||||||
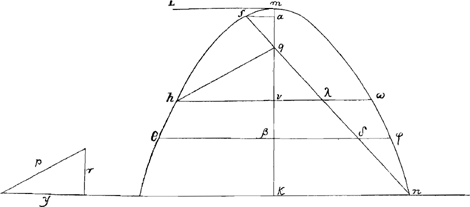
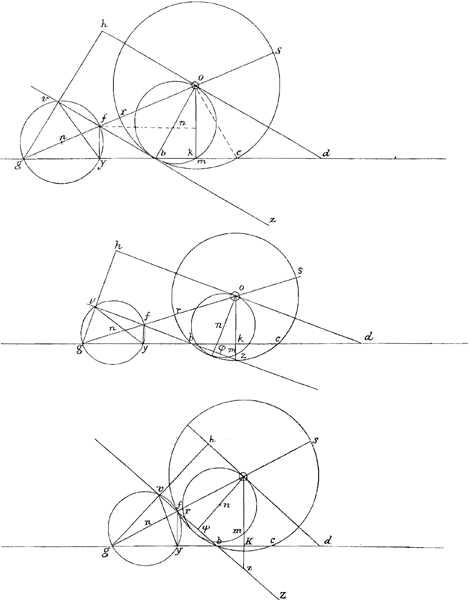
Constructio.Supponamus factum esse quod postulatur, et y Π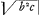 , vel y Π , vel y Π 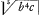 ,Ga naar voetnoot2) et caetera, hoc est y aequari majori ex duabus, vel quatuor medijs proportionalibus quaesitis et caetera. 2o accipiatur quaeuis recta, quae vocetur r major vel minor ipsâ y, id autem facile fiet cum vero proximus sciri possit valor ex y. 3o si r major sit quam y, fiat Δum rectangulum, cujus hypothenusa sit r, et facilitatis gratia tantum non necessitatis sit y minus latus rectum angulum subtendens, p verò alterum latus. Si vero y major sit ipsâ r, jungantur illa ad angulum rectum, ducaturque p, vt fiat etiam Δlum rectangulum ryp, quando videlicet duas inter b, et c medias proportionales quaerimus; vel si inter easdem b, et c quatuor medias proportionales inuenire lubet factum cogitetur Δum rectangulum, cujus latera rectum angulum subtendentia eandem inter se proportionem habeant quam y2 ad r2, et ea deinceps methodo pro caeteris medijs proportionalibus inueniendis. 4o eligatur, vt praeceptum est, aliqua curua regularis, quae sit verbi gratia parabola θ m ϕ, cujus vertex sit m, axis
mk, parameter, siue latus rectum m L. Tum infra verticem sumpto in axi arbitrario puncto q, factum putetur Δum qhv, simile Δlo ryp, ita ut punctum h in ipsa parabola reperiatur. Nunc vero in Δlo ryp junctae sint ad perpendiculum r minor, et y major. Postea sic producatur hv, vt parabolam secet in puncto w. Deinde signato infra punctum v quouis puncto k per ipsum transeat ordinata kn, et per puncta m et q agatur recta nq, eovsque producta donec occurrat parabolae in puncto s, ducaturque ordinata sa. Demum accepto inter k, et v arbitrario puncto β, per ipsum transeat ordinåta θβδϕ. ,Ga naar voetnoot2) et caetera, hoc est y aequari majori ex duabus, vel quatuor medijs proportionalibus quaesitis et caetera. 2o accipiatur quaeuis recta, quae vocetur r major vel minor ipsâ y, id autem facile fiet cum vero proximus sciri possit valor ex y. 3o si r major sit quam y, fiat Δum rectangulum, cujus hypothenusa sit r, et facilitatis gratia tantum non necessitatis sit y minus latus rectum angulum subtendens, p verò alterum latus. Si vero y major sit ipsâ r, jungantur illa ad angulum rectum, ducaturque p, vt fiat etiam Δlum rectangulum ryp, quando videlicet duas inter b, et c medias proportionales quaerimus; vel si inter easdem b, et c quatuor medias proportionales inuenire lubet factum cogitetur Δum rectangulum, cujus latera rectum angulum subtendentia eandem inter se proportionem habeant quam y2 ad r2, et ea deinceps methodo pro caeteris medijs proportionalibus inueniendis. 4o eligatur, vt praeceptum est, aliqua curua regularis, quae sit verbi gratia parabola θ m ϕ, cujus vertex sit m, axis
mk, parameter, siue latus rectum m L. Tum infra verticem sumpto in axi arbitrario puncto q, factum putetur Δum qhv, simile Δlo ryp, ita ut punctum h in ipsa parabola reperiatur. Nunc vero in Δlo ryp junctae sint ad perpendiculum r minor, et y major. Postea sic producatur hv, vt parabolam secet in puncto w. Deinde signato infra punctum v quouis puncto k per ipsum transeat ordinata kn, et per puncta m et q agatur recta nq, eovsque producta donec occurrat parabolae in puncto s, ducaturque ordinata sa. Demum accepto inter k, et v arbitrario puncto β, per ipsum transeat ordinåta θβδϕ.
| |||||||||||||||||||
Analysis.Δ hqv simile est Δryp. Igitur r.y∷qv. hv. Id est r.y∷v. yv/r Π hv, et y2v2/rrΠ (□to hv Π)+Lv+Lm propter parabolam, Igitur +y2v2Π+Lr2v+Lmr2, et totum per y multiplicando habetur +y3v2Π+Lr2yv+Lmr2y, et mutando y3 in valorem, quem in deprimenda aequatione +y3Π+b2c obtinet fit +b2cv2Π +Lr2yv+Lmr2y, siue pro +bbc scribendo +rrρ, et omnes terminos per +rrρ diuidendo oritur +vvΠ +Lyv+Lmy/+ρ. Quare +vΠ +½Ly+/ρ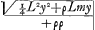 , et si breuitatis causa + , et si breuitatis causa + 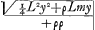 vocetur z fiet
+vΠ+½Ly+ρz/+ρ, cui vocetur z fiet
+vΠ+½Ly+ρz/+ρ, cui
| |||||||||||||||||||
[pagina 549]
| |||||||||||||||||||
addita mq Π m habetur +ρm+½Ly+ρz/+ρ Π + MV quae multiplicata per mL Π L efficit +ρLm+½L2y+ρLz/+ρ Π□ hv propter parabolam. Igitur
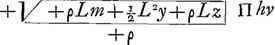 Atqui kn. kq∷vλ. vq. Id est n. k∷vλ. +½Ly+ρz/+ρ. Igitur +½Lny+ρnz/+ρk Π vλ, quae addita, et detracta ex hv Π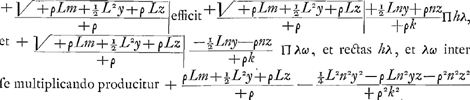 Π□hλω, siue totum per +ρ2k2 multiplicando, et terminos ordinando habetur 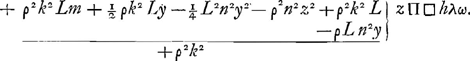 zΠ□hλω. Rursus kq. qn≤∷qv∶qλ. Id est k. q∷+½Ly+ρz/+ρ. +½Lqy+ρqz/+ρkΠqλ, quae addita ad sqΠs, et detracta ex qnΠq efficit + ρks+½Lqy+ρqz/+ρkΠsλ, et +ρkq-½Lqy-ρqz/+ρkΠλn, et rectas + sλ, et + λn in se ducendo fit 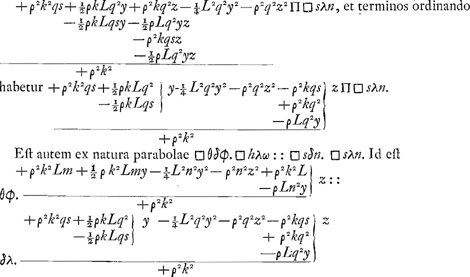 | |||||||||||||||||||
[pagina 550]
| |||||||||||||||||||
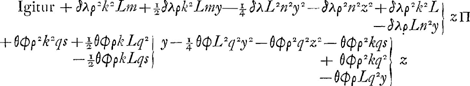 et ordinata aequatione habetur 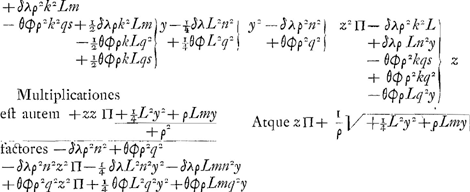 Et factis in inuenta aequatione hisce mutationibus ex zz et z in inuentos valores, sic stabit aequatio. 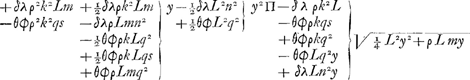 Jam antequam hi termini breuiores reddantur considerandum est quod dum vtraque aequationis pars in se ducetur, vt surdum euanescat, terminus qui ab y4 denominabitur idem omnino futurus est in vna aequationis parte quam in altera. Nam in prima parte habebitur quadratum binomij 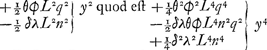 In secunda vero quadratum binomij 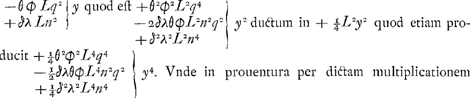 aequatione excidet terminus ab y4 denominatus, et ipsa aequatio vi sua ad tertium gradum deuoluetur. Praeterea sciendum est quod si traditâ methodo quatuor medias proportio- | |||||||||||||||||||
[pagina 551]
| |||||||||||||||||||
nales inter b, et c quaesiuissem nihil ideo diuersi in opere accidisset, nec aequatio ab y denominata plures dimensiones habuisset, nam sic analysim instituissem r.2y2∷qv.hv id est r2.y2∷v. y2v/rr Πhv. et +y4v2/+r4 Π(□hvΠ) + Lv + Lm ob parabolam, et totum per y multiplicando sit +y5v2Π + Lr4yv + Lmr4y, et mutando y in valorem, quem in deprimenda aequatione +y5Π + b4c obtinet sit +b4cv2Π + Lr4yv + Lmr4y, siue pro b4c scribendo r4ρ, et omnes terminos per r4ρ diuidendo habetur vt prius +vvΠ +Lyv+Lmy/ρ. Atque hinc saltem concluditur modo reales existant inuentae aequationis termini, omnes quae in vniuersalis mesolabij inuentione occurrunt difficultates ad inuentionem duarum mediarum proportionalium redactam esse. Primo igitur videndum est vtrum inuentae aequationis termini euanescant, et id quidem in vno experiri sufficiet, nam si in aequatione, cujus omnes termini ab vna parte stantes nihilo sunt aequales, corum aliquis non destruatur saltem superesse debet vnus e reliquis, qui sua affirmatione, uel negatione hunc realem terminum elidere possit, vt eo quo dictum est modo ordinata aequatio nihilo maneat aequalis. quare ad hunc effectum eligamus vltimum terminum nempe +δλρ2k2Lm-θϕρ2k2qs cum caeteris simplicior sit, et ponamus si fieri potest +δλρ2k2Lm-θϕρ2k2qsΠο vel totum per ρ2k2 diuidendo erit +δλLmΠ+θϕqs. vt autem valores quantitatum θϕ, et δλ inueniamus sic procedendum. Ponatur βδΠe. Jam kn. kq∷βδ. βq. Id est n. k∷e.ke/nΠβq, cui addita mqΠm fit +mn+ke/+n Πβm, quae ducta in m LΠL sit +Lmn+Lke/+nΠ □ to θβ ob parabolam, ergo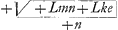 Πθβ, cui addita, et ab eadem detracta +βδΠ+e habetur Πθβ, cui addita, et ab eadem detracta +βδΠ+e habetur 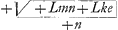 +eΠθδ, et +eΠθδ, et  -eΠδϕ, et rectas θδ, et δϕ inter se multiplicando fit +Lmn+Lke-ne2/+n Π(□θδϕΠ) θϕ, quod ductum in qs efficit +Lmnqs+Lkqse-nqse2/+nΠθϕqs. -eΠδϕ, et rectas θδ, et δϕ inter se multiplicando fit +Lmn+Lke-ne2/+n Π(□θδϕΠ) θϕ, quod ductum in qs efficit +Lmnqs+Lkqse-nqse2/+nΠθϕqs.
Rursus kn. nq∷βδ. δq. Id est n. q∷e. qe/nΠδq, quae addita ad sqΠs, et detracta ex nqΠq fit +ns+qe/+n Πsδ. et +qn-qe/+nΠ+δn, et rectas sδ, et δn inter se multiplicando habetur
in Lm efficit | |||||||||||||||||||
[pagina 552]
| |||||||||||||||||||
et totum per n2 multiplicando, et aequationem ordinando habetur
+Lmns+Lkns-Lmnq/+n2s-Lmq Πe, siue mutando nn in suum valorem +Lm+Lk, et totum per L diuidendo oritur +mns+kns-mnq/+ms+ks-mq Πe. Id est +n Π +e quod est impossibile, nam hac ratione non fieret □δλ. Igitur +δλLm non est aequale θϕqs, nec in inuenta aequatione terminus +δλρ2k2Lm-θϕρ2k2qs destruitur, et consequenter in eadem aequatione saltem supererit vnus e reliquis ab y denominatus, qui hunc vltimum elidat, vt ipsa aequatio ordinata nihilo maneat aequalis. Vnde etiam indubitatum manet omnem quae in inueniendo Mesolabo reperitur difficultatem saltem ad vnius aequationis tres dimensiones habentis solutionem redactum esse, quod profecto mirum videri debet. Nam Cartesius, qui omnium primus Mesolabum vniuersale est aggressus, vt quatuor tantummodo medias proportionales inueniat, curuam lineam conicis sectionibus compositiorem describere illamque per suam methodum circulo secare coactus est, pro caeteris vero medijs proportionalibus videlicet pro sex, alijsque per pares numeros designatis viam tantum ostendit qua inueniri debeant, et quae in eo consistit vt curuas lineas gradatim magis ac magis compositas effingamus, illasque pariter circulis secemus, hic vero pro omnium inuentione vna eademque trimensa aequatio adhibitur, per cujus solutionem ad optatum finem feliciter peruenire conceditur. Jam vero vt ad duarum mediarum proportionalîum inuentionem redeamus, quoniam in prouentura aequatione ad tertium gradum assurgence, termini tam ab y, quam ab yy denominati reperientur, ac terminus ab y3 denominatus omnino cognitus euadet mutando videlicet y3 in suum valorem +bbc, tandem inuenta aequatio a 4to gradu in 3um delapsa in 2do subsistet, adeo vt si hujus depressae aequationis termini non euanescant optatum habebitur. Videndum itaque restat vtrum reales futuri sint dictae aequationis termini, et id quidem vt prius in vno tentare satis erit ob allatas rationes. Ad hunc finem eo termino vtamur, qui denominationem suam ab y accepturus est, quoniam omnium simplicissimus videtur, illum autem per sequentes operationes inueniemus. | |||||||||||||||||||
[pagina *29]
| |||||||||||||||||||
 |
| ||||||||||||||||||

