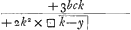Oeuvres complètes. Tome VI. Correspondance 1666-1669
(1895)–Christiaan Huygens–
[pagina 553]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1um Lemma ex Vieta.Si in circulo obc inscripta bc producatur ad dGa naar voetnoot1), ita ut bd sit dupla bc, jungaturque od, cui agatur a puncto b parallela fb. Tum a puncto o. ad rectam gb ducatur og, ita ut intersegmentum gf sit aequale or. Dico rs. gb. gr. be∺. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Demonstratio.Ex hypothesi ad parallela est rectae fb. Igitur gf. gb∷(fo Π) gr. bd. Atqui gf. rs∷bc. bd. Quare rs. gb∷gr. bc, et rs. gr∷gb. bc, et alterne componendo gs. gc∷gr. bc. Est autem □ sgr Π□ cgb. Igitur gs. gc∷gb. gr.∷gr. bc. ergo rs. gb. gr. bc ∺ vt erat ostendendum. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Problema.Inter duas datas rectas lineas duas medias proportionales inuenire per planorum doctrinam. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Datum.Dentur duae rectae 2r major, et c minor, inter quas inueniendae sint duae mediae proportionales. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Constructio.Centro o, interuallo or, vel os Πr fiat circulus obc, in quo aptetur bc aequalis c supponatur autem per lemmatis doctrinam inter rs, et bc siue inter 2r, et c inuentas esse duas medias proportionales gb, et gr vt in diagrammate apparet. Tum ex punctis o, et f ducantur ok, et fy perpendiculares ad gd, atque ob in 1a figura vel oϕ in alijs figuris perpendicularis ad fz. Deinde super ob, vel oϕ atque etiam super gf, spatio no, et ngΠ ½r describantur circuli nom, ngy transeuntes per puncta, f, et o, et quidem circulus bom tanget hd in puncto o, ob rectarum bo vel qo, et hd inter se perpendicularitatem, circulus vero ngy secabit rectam fb quousque opus erit productam in aliquo puncto vt in v quoniam vf obliqua est ad gf, ut transibit | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 554]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
per punctum y nam angulus gyf est in semicirculo gfy, demum ducta ov producta donec occurrat od in puncto h, agatur vy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Analysis 1a.Ex 1o lemmate rs. gb. gr. bc ∺ Id est 2r. gb. gr. c ∺ ergo gb Π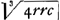 , et gr Π , et gr Π 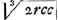 . Jam vero y f. fg ∷ ko. og. id est y. r ∷ k. kr/y Π go, et gr vel fo Π+kr-ry/y Π . Jam vero y f. fg ∷ ko. og. id est y. r ∷ k. kr/y Π go, et gr vel fo Π+kr-ry/y Π 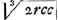 et vtramque partem cubando habetur +k3r3-3k2r3y +3kr3y2-r3y3Π+2rccy3. ergo +2cc y3-3kr2y2+3k2r2y-k3r2 Π o siue rr +d2y3-3kr2y2+3k2r2y-k3r2 Π o nam 2c2 Π dd.
+r2 et vtramque partem cubando habetur +k3r3-3k2r3y +3kr3y2-r3y3Π+2rccy3. ergo +2cc y3-3kr2y2+3k2r2y-k3r2 Π o siue rr +d2y3-3kr2y2+3k2r2y-k3r2 Π o nam 2c2 Π dd.
+r2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Analysis 2a.gf. fo∷gb. bd. Id est r. kr-ry/y∷gb. 2c ergo +2cy/+k-y Π gb, et addita c fit +ck+cy/+k-y Π gc quae ducta in gb Π +2cy/k-y dat +2c2ky +2c2y2/+ k2-2ky+y2 Π□ cgb. Jamvero gr Π+ky-ry/y, et gs Π +kr+ry/y et has rectas in se ducendo fit +k2r2-r2y2/yy Π□ sgr Π□ cgb Π +2c2ky+2c2y2/+k2-2ky+y2. Igitur +k4r2-2k3r2y+k2r2y2+2kr2y3-r2y4Π+2c2ky3+2c2y4 -k2r2 et ordinata aequatione habetur +d2y4+2c2ky3+2k3r2y-k4r2Πο. -2r2k | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Analysis 3a pro 2do casu. Quando bz secat circulum infra punctum b.ko. od ∷ yf. fb id est k.d ∷ y.dy/k Π fb, cui addita bz Π z fit +kz+dy/k Π fz. et rectas fb, et fz in se ducendo habetur +dkzy+d2y2/+kk Π□ zfb. Jam vero ex pro- | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 555]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
batis go siue fs Π +kr/y, et fr Π +kr-2ry/y, et rectas fs, et fr in se ducendo habetur +k2r2-2kr2y/+yy Π□sfrΠ□zfbΠ) +dkzy+d2y2/+kk. Ergo + d2y4+dkzy3 +2k3r2y-k4r2Πο. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Annotatio.Ex comparatione hujus, et penultimae aequationis inuenitur zΠ+2cc-2rr/d, quae est vna ex inscriptis in circulo. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Analysis 4a.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 556]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cΠr excidit terminus ab y3 denominatus ac relinquitur +d2y4+2k2r3y-k4r2Πο. et hanc aequationem per +3c, ac vltimo inuentam per d multiplicando fit + 3cdy4
ac d deleto vtrimque communi termino +3cd2y4, et reliquis per kr diuisis, atque mutato c in r habetur
Est autem ex analysi 1a +d2y3Π+3kr2y2-3k2r2y+k3r2, et in praecedenti aequatione mutando +d2y3 in suum valorem, et omnibus terminis per k diuisis fit
per 1 am analysim, et deleto vtrimque communi termino -2d2y3, ac ordinata aequatione habetur
Atqui in vltimo termino +dm-rr × +4dk2Π+4d2k2m-4dk2r2, estque dm major quam rr, vt statim ostendam igitur +4d2k2m-4dk2r2 est quantitas realis et affirmata, quae juncta quantitati affirmatae +2k3r2 efficit vltimum inuentae aequationis terminum realem, et affirmatum, Igitur in inuenta aequatione superest saltem vnus e reliquis terminis q ab y denominatis, qui sua negatione hunc realem terminum elidat, vt ipsa aequatio nihilo, sicut ordinata est, fiat aequalis. Quod erat ostendendum. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemma.Ostendere in prima figura quando c Π r, rectam om Π ok, siue puncta k, et m in vnum coincidere, ac simul dm siue dk majorem esse quam rr. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Demonstratio.Ex hypothesi recta bc aequatur radio oc vel ob ergo ∠lus boc est 60 graduum, sed ex hypothesi etiam rectae oc Π recta cd ergo ∠ lus cod est 30 graduum cui addito ∠ 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 557]
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
koc etiam 30 graduum erit ∠lus dvk 60 graduum aequalis ∠10 in circuli cujus centrum est n segmento orm inscriptibili, ergo recta om latus est trigoni aequilateri in circulo norm inscriptibili et quia hujus circuli radius aequatur ½ r erit recta om Π 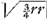 hoc est recta om Π k.
Deinde quia ddΠ+2cc+rr, hoc est hîc ddΠ3rr erit dΠ+r hoc est recta om Π k.
Deinde quia ddΠ+2cc+rr, hoc est hîc ddΠ3rr erit dΠ+r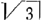 , quae ducta in om, siue okr aequali +r , quae ducta in om, siue okr aequali +r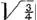 habetur+3/2rr major quam rr vt erat ostendendum. habetur+3/2rr major quam rr vt erat ostendendum.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Analysis 5a pro 2do casu.
bfΠ +dy/k cui addita bϕ Π b habetur +bk+dy/k Πfϕ, et huic adhuc additâ vf Π v fit +bk+dy+kv/k Π (vϕΠhoΠ) +kv/y. Ergo +bky+dyy+kyv Π +kkv, et sic +bky+dyy/+k×k-y Πy quae ducta in py Π+cky+3cyy/+2k×k-y efficit +bck2y2+cdky3+3cdy4Π□ vf×gy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| +bck2y2+cdky3+3cdy4 | |
| +3bck | datGa naar voetnoot4). |
| _____ | |
+2k2× □ 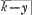 |
- voetnoot1)
- Voir la planche vis-à-vis de cette page.
- voetnoot2)
- La notation k×k-y désigne le produit k(k-y).
- voetnoot3)
- C'est ici que Huygens a commencé la correction indiquée dans la Lettre No. 1790: correction qu'il n'a pas continuée, et que par conséquent nous n'avons pas reproduite.
- voetnoot4)
- Le reste de cette pièce n'a pas été trouvée.


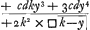 Π□vf×gy.
Deinde fb.bo ∷ vf. gv id est +dy/k. r∷+dyy/+k×k-y. +ry/+k-yΠvg quae ducta in fy Π+y dat +ryy/+k-y Π□gv×fy, cui addito
Π□vf×gy.
Deinde fb.bo ∷ vf. gv id est +dy/k. r∷+dyy/+k×k-y. +ry/+k-yΠvg quae ducta in fy Π+y dat +ryy/+k-y Π□gv×fy, cui addito