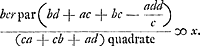Oeuvres complètes. Tome V. Correspondance 1664-1665
(1893)–Christiaan Huygens–No 1434.
| |
[pagina 420]
| |
vreemde toevallen, die ons daer in soo langh ophouden. VE moet niet dencken dat ick al lachende seyde in 't eynde van mijne laetsteGa naar voetnoot1) dat ick wederom eenighe correctie verwachte, want ick vertroude noijt mij selfs soo veel toe als te gelooven dat ick in 't rekenen jae selfs in 't ratiocineren geen dwaelinge onderworpen soude sijn; en ick ben nu noch veel blooder als te voren; siende dat de Heer Hudde naer dat hij sijn rekeninghe tot 2 a 3 maelen hadde oversien en met wackere sinnen verbetert 't geen hij al sluymerende gepecceert hadde, en alles door 2 verscheyde wegen uyt gevonden die hem de selfde uijtkomst gaven, siende, segh ick, dat hij niet tegenstaende dit alles sich heeft konnen vergissen. Hij sal hier van voorseecker vremdt toe hooren, en noch meer als ick sal derven seggen dat in mijn rekeningen geen faut is geweest, en dat hij en ick op een selfde questie een selfde uytkomst krijgende, ick wel gereeckent hebbe en hij qualijck. alle 't welcke ick nochtans onder correctie, alhier sal doen blijcken. Ende beginnende van VE generalen regel
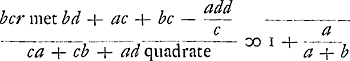 met x, soo segh ick dat VE volgens de selve spelende en de partije van A nemende apparent sijn gelt soude verliesen. want gevende aen A 1 witte en 1 swarte schijf, dat is stellende a ∞ 1 en b ∞ 1. maer aen B 1000 witte schijven en 1 swarte, so komt volgens qui nous y retiennent si longtemps. Vons ne devez pas penser que je badinais en disant à la fin de ma dernièreGa naar voetnoot1) que j'attendais de nouveau quelque correction, car jamais je n'ai eu une telle confiance en moi-même que de croire que dans le calcul et même dans le raisonnement je ne serais pas sujet à l'erreur, et maintenant je suis encore bien plus timide que ci-devant, en voyant que Monsieur Hudde, après avoir revisé son calcul jusqu'à 2 ou 3 fois, et après avoir corrigé d'un esprit éveillé ce qu'il avait pêché en sommeillant, et ayant tout trouvé par 2 voies différentes, qui lui donnèrent le même résultat - en voyant, dis-je, que nonobstant tout cela, il a pu se tromper. Il sera fans doute étrangement surpris d'entendre ceci, et encore plus quand j'oserai affirmer qu'il n'y a pas eu de faute dans mes calculs et que, lorsque lui et moi nous avons obtenu un même résultat pour une même question, moi j'ai calculé juste et lui mal. Tout cela je le ferai voir ici, pourtant sauf correction. | |
[pagina 421]
| |
desen regel 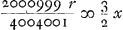 dat is dat is 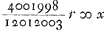 , soo dat x ofte de winste van B op ieder spel soude wesen min als ⅓ r, dat is ⅓ van een ducaet of van 't geen op het trecken van een swarte schijve ieder reyse werdt ingeset. Als B dan aen A in 't begin van ieder spel ⅓ van een ducaet gaf soo soude VE meenen dat A wel toe quam. Maer dewijl A van eersten aen een kans tegen een heeft om gelijck te gaen, of om een ducaet in te moeten setten, dat is, of om een ducaet soo goedt als quijt te sijn, dewijl het 1000 tegen 1 is of B sal die weghstrijcken, soo volght uijt het 1. voorstel van mijn Tractatien van dobbel rekeningen dat A seer weynigh min verliest als ½ ducaet, soo dat met het aennemen van ⅓ ducaet hij ontrent ⅙ ducaet op ieder spel soude toegeven. VE kan dan hier uijt verstaen dat sijn regel niet recht is, doch waer uijt eygentlijck de faute ontstaen is, en kan ick uijt het gheene hij van sijne methode maer ten halven heeft gelieven te expliceren, niet nae speuren. Maer door de mijne, die seer simpel is, en VE qualijck kan onbekent sijn, dewijl alleen het 3de voorstel van mijn voorszegde tractatien, beneffens de kennisse der oneindige progressien daer toe van nooden is, door dese dan vind ick dat de waeren regel is , soo dat x ofte de winste van B op ieder spel soude wesen min als ⅓ r, dat is ⅓ van een ducaet of van 't geen op het trecken van een swarte schijve ieder reyse werdt ingeset. Als B dan aen A in 't begin van ieder spel ⅓ van een ducaet gaf soo soude VE meenen dat A wel toe quam. Maer dewijl A van eersten aen een kans tegen een heeft om gelijck te gaen, of om een ducaet in te moeten setten, dat is, of om een ducaet soo goedt als quijt te sijn, dewijl het 1000 tegen 1 is of B sal die weghstrijcken, soo volght uijt het 1. voorstel van mijn Tractatien van dobbel rekeningen dat A seer weynigh min verliest als ½ ducaet, soo dat met het aennemen van ⅓ ducaet hij ontrent ⅙ ducaet op ieder spel soude toegeven. VE kan dan hier uijt verstaen dat sijn regel niet recht is, doch waer uijt eygentlijck de faute ontstaen is, en kan ick uijt het gheene hij van sijne methode maer ten halven heeft gelieven te expliceren, niet nae speuren. Maer door de mijne, die seer simpel is, en VE qualijck kan onbekent sijn, dewijl alleen het 3de voorstel van mijn voorszegde tractatien, beneffens de kennisse der oneindige progressien daer toe van nooden is, door dese dan vind ick dat de waeren regel is
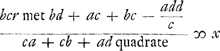 vant cette règle | |
[pagina 422]
| |
volgens welcke het verlies van A in mijn eerste questie van kruijs of munt geen 4/27 r is maer 2/9 r. En in de 3de questie de winst van A geen 9/245 maer 3/49. Maer dewijl ick mede inde eerste questie hebbe gevonden als VE 4/27 r, en inde 3de 207/343 r soo staet nu te seggen hoe ick wel gerekent hebbe. VE dan moet weten dat ick int voorstellen van mijne questien door inadvertentie naer gelaten hebbende int eynde daer bij te voegen dat ick verstondt dat het spel niet en eyndigde sonder dat van d'een of d'ander sijde iets was ingeset, soo is daer uyt gevolght dat VE gestelt heeft dat A ten eersten kruijs werpende of een witte schijf treckende het spel daer mede uijt was, en ick beken dat mijne slofficheijt hier d'eerste oorsaeck toe gegeven heeft. maer VE faute in 't rekenen heeft mij belet te bemercken dat daer eenigh misverstand uijt geresen was want korts naer het afsenden van mijne laestenGa naar voetnoot2) gewaer geworden sijnde dat dese omissie konde een andere interpretatie veroorsaecken aen mijn Problemata, soo en konde ick nochtans niet vermoeden sulx in der daet gebeurt te sijn dewijl ick sagh dat VE met mij een selfde uytkomst vondt van 4/27 r in de questie van kruijs of muntGa naar voetnoot3), welcke overeenkomst suivant laquelle la perte de A dans ma première question de croix ou pile n'est pas 4/27 r, mais 2/9r. Et dans la 3e question le gain de A n'est pas 9/245 mais 3/49. | |
[pagina 423]
| |
in der daet seer seltsaem is. Ick gingh noch ten overvloedt, soo ick meende, dese selfde questie uijtrekenen volgens d'interpretatie daer ick sagh oorsaeck toe gegeven te hebben, doch vindende als dan 2/9r en geen 4/27r, soo hieldt ick mij ten vollen verseeckert dat VE de selfde sin als ick gevat hadde, en dachte daerom onnoodigh VE iets dien aengaende te laten weten. Hier door is ook geschiedt dat ick de 2de questie sijnde van gelijck spel niet mede op d'andere maniere geproeft hebbe te solveren, 't welck in dien gedaen hadde soude daer door gevonden hebben dat VE Regel van c ∞ ad/a + b in dien sin goedt was gelijck se in der daet is en daer door in bedencken gekomen sijn van de tweederley interpretatie. Ick hebbe dan alle onse questien met de boven verhaelde clausula altijds geconsidereert, vastelijck gelovende om de reden hier gesecht dat VE van gelijcke dede. Ende VE sal vinden dat mijn regel van cc ∞ - dc + aadc/ab + bb + add/b, goet is, volgens den sin die ick mij ingebeelt hadde, ende soo mede mijn getallen in de andere questien gevonden, te weten 4/27r, 207/343r en 105/131r, bij aldien VE de moeijte wil nemen van 't selve nae te sien, ende sal te gelijck sien dat de generale solutie deser questien op dese manier wat meer moeytens heeft als wel op de manier soose VE heeft genomen. est certainement fort singulière. Par surcroit, à ce que je croyais, je calculai cette même question selon l'interprétation à laquelle je vis avoir donné occasion; mais trouvant dans ce cas 2/9 r et non 4/27 r, je me tins pleinement assuré que vous l'aviez prise dans le même sens que moi, et par conséquent je ne jugeai pas nécessaire de vous en faire savoir quelque chose. Et par là il est arrivé aussi que je n'ai pas cherché à résoudre la 2e question, celle de jeu égal, pareillement de l'autre manière; si je l'eusse fait, j'aurais trouvé que dans ce sens votre règle de c ∞ ad/a + b était bonne, comme elle l'est en effet, et ainsi l'idée me serait venue de l'interprétation double. J'ai donc toujours considéré toutes nos questions avec la clausule susdite, croyant fermement, par la raison mentionnée, que vous faisiez de même. Vous trouverez que ma règle de cc ∞ - dc + aadc/ab + bb + add/b est bonne, selon le sens que j'avais imaginé, et que bons aussi sont les nombres que j'ai obtenus dans les autres questions, à savoir 4/27 r, 207/343 r et 105/131 r, si vous voulez bien prendre la peine de les vérifier; et vous verrez, en même temps, que la solution générale de ces questions, de cette manière, donne un peu plus de peine que de la manière dont vous les avez prises. | |
[pagina 424]
| |
Eyndelijck wat aengaat de 4de questie hier is het seecker dat wij de Propositie op de selfde manier verstaen. Ende VE de selve door diergelijcke methode als de 2de berekenende soo is daer door tot de rechte solutie gekomen die de selfde is als de mijne. dus vele noch van dese materie genootsaeckt wesende te schrijven, sal hier mede eyndigende ende het eijnde van dese onse Exercitatie te gemoet siende, blijven
Mijn Heer
VE dienstwillige dienaer Huygens de Z. Enfin, quant à ce qui regarde la 4e question, ici il est certain que nous entendons la proposition de la même manière. Et en la calculant par une méthode analogue à celle de la 2e, vous êtes arrivé ainsi à la bonne solution, qui est la même que la mienne. |
|