Oeuvres complètes. Tome V. Correspondance 1664-1665
(1893)–Christiaan Huygens–
[pagina 391]
| |
No 1427.
| |
[pagina 392]
| |
gens welcke A wint 207/343 van een ducaet, in plaets dat VE gevonden heeft 9/245 van een ducaet. Ende ick en twijffel niet of VE sijn rekening oversiende gelijck hij soo ick meene door het volgende sien sal daer reden toe te hebben, sal mijn uijtkomst waer bevinden. In VE questie daer A weder eerst kiest uijt 2 witte en 1 swarte ende werd gevraeght uijt wat getal van witte en swarte B soude moeten kiesen om te maecken dat beijde haer kanssen gelijkwaerdigh wierden, hier vind ick dat VE solutie en de mijne beijde gemist sijn, VE houdende dat de witte schijven tot de swarte van B moeten sijn als 2 tot 3, en ick dat het getal der witte en swarte gelijck moest sijn. Maer de rechte proportie is volgens mijn verbeterde rekening (daer door ick bevond een + voor een - gestelt te hebben) dese volgende, te weten, als men stelt dat de reden der witte totte swarte schijven is als c tot d soo komt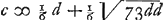 . soo dat de proportie der witte en swarte schijven in geen rationale getallen hier kan gegeven werden, maer wel ten naesten bij; ende als B hadde 11 witte en 7 swarte, soo soude hij noch een weijnigh aen de quaetste koop sijn, daer in tegendeel VE hem minder witte als swarte toeleght. . soo dat de proportie der witte en swarte schijven in geen rationale getallen hier kan gegeven werden, maer wel ten naesten bij; ende als B hadde 11 witte en 7 swarte, soo soude hij noch een weijnigh aen de quaetste koop sijn, daer in tegendeel VE hem minder witte als swarte toeleght.
Als men voorts met VE de reden der witte tot de swarte schijven van A, die eerst werpt, stelt te sijn als a tot b. En de witte tot de swarte van B als c tot d. soo suivant lequel A gagne 207/343 d'un ducat, au lieu que vous avez trouvé 9/245 d'un ducat. Et je ne doute aucunement que vous ne trouviez mon résultat exact, lorsque vous reviserez votre calcul, comme il y aura lieu pour vous, à ce que je crois, en voyant ce qui suit. | |
[pagina 393]
| |
vind ick dat om de kanssen gelijckwaerdigh te maecken, den generalen regel is dese cc ∞ - dc + aadc/ab + bb + add/b. In plaets van welcke VE desen geeft ca + cb ∞ ad ofte c ∞ ad/a + b. dit groote verschil en oock dat VE schrijft dat dese VE questie van gelijcke kanssen lichter valt te ontbinden volgens VE methode als mijn eerste van kruijs of munt, doet mij voor vast houden, dat wij gansch verscheijde wegen volgen. Staet te besien wie de rechte gekosen heeft. Ende wat mij aengaet ick vertrouw soo wel op den voorgaenden regel die ick hier gestelt heb dat ick volgens deselve wel een kans soude derven waghen, nemende de partije van A of B die men soude mij willen geven. Maer indien VE mij van gelijcken presenteerde met sijn regel te willen doen ick soude mij van de winst verseeckert houden, want nemende de partije van A en VE die van B laetende, en gevende aen A 10 witte en 1 swarte schijf, soo komt volgens VE regel 11 c ∞ 10 d. dat is voor B 10 witte en 11 swarte schijven. waer door de kansse van A soo veel beter is als die van B dat oogenschijnelijck blijckt, en noch beter als men de proportie der witte totte swarte van A noch grooter stelt. A wint hier volgens mijn regel die ick hier toe hebbe 105/131 van t geen men ieder reijse inset. Wat aengaet mijne laatste questie van kruijs of munt om de kanssen van A en B alors je trouve que pour rendre les chances équivalentes, la règle générale est cc ∞ dc + aadc/ab + bb + add/b. Au lieu de laquelle vous trouvez celle-ci: ca + cb ∞ ad ou c ∞ ad/a + b. Cette grande différence, et aussi ce que vous écrivez que cette question de chances équivalentes, proposée par vous, est plus aisée à résoudre suivant votre méthode que ma première de croix ou pile, m'assure que nous suivons des voies toutes différentes. Reste à voir qui a choisi la bonne. Et quant à moi, je me fie tant à la règle précédente que j'ai posée ici, que j'oserais bien risquer une chance suivant elle, en prenant la partie de A ou de B, que l'on voudrait me donner. Mais si vous m'offriez d'en faire de même quant à votre règle, je me sentirais sûr du gain; car prenant la partie de A et vous laissant celle de B, et donnant à A 10 jetons blancs et un noir, il vient suivant votre règle 11 c ∞ 10 d. c'est-à-dire pour B 10 jetons blancs et 11 noirs; par conséquent la chance de A sera d'autant meilleure que celle de B, ce qui paraît clairement, et encore mieux quand on prend la proportion des jetons blancs aux noirs de A encore plus grande. Ici A gagne d'après ma règle, qui me sert ici, 105/131 de ce que l'on met chaque fois. | |
[pagina 394]
| |
gelijck te maecken, hier vind ick de selfde uijtkomst met VE, te weten dat ieder van eersten aen 2/3 van een ducaet moet insetten. Van de 2de der 5 questien in 't eijnde van mijn TractaetienGa naar voetnoot2) en vind ick geen rekening onder mijn papieren, maer de reden waer om ick de getallen 232. 159. 104 voor goet hebbe laeten gaen, al hoe wel alleen t middelste sodanig was, kan dese wesen dat ick de kans van B gerekent hebbende, (want nae mijn manier werdt ieder bijsonder gerekent) en die vindende met VE rekening te accorderen, hebbe geen verder moeijten noodigh geacht. gelijck nu weder terstond het deel van C gerekent hebbe te sijn 7/33 van tgeen instaet. ende hier is soo weijnigh cijfferens toe van noden dat ick uijt de goede of quade uijtkomst geen consequentie soude willen maecken tot het geene mij in de bovenschreven swaerder questien soude moghen gebeurt sijn. Het glas van Monsieur Vossius daer VE soo veel goets van geseght is heb ick dickwils genoeg gesien om VE te konnen verseeckeren dat het min als middelmatigh is, en werdt oock van hem voor niet anders gehouden. sijnde ontrent 2½ duijm breet, en geen opening als van 1⅓ duijm lijdende. en dat tot een verkijker van 28 of 29 et de B, ici je trouve le même résultat que vous, à favoir que chacun doit mettre de premier abord 2/3 d'un ducat. | |
[pagina 395]
| |
voet. Is oock maer tamelijck geslepen, niet te Romen maer te Brussel van een onbekendt meester, ende is aen Vossius te Parijs verkocht voor 7 of 8 pistolen. Eijndigende ende weder eenige correctie van mijne correctien verwachtende blijve
Mijn Heer VE dienstwiligen dienaer ocrement, non à Rome, mais à Bruxelles par un maître inconnu, et a été vendu à Vossius à Paris pour 7 ou 8 pistoles. |
|


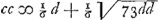 ; de sorte que l'on ne peut pas donner la proportion des jetons blancs et noirs en nombres rationnels, mais seulement par à peu près; et si B avait 11 jetons blancs et 7 noirs, il serait encore un peu désavantagé; tandis que, au contraire, vous lui donnez moins de jetons blancs que de noirs.
; de sorte que l'on ne peut pas donner la proportion des jetons blancs et noirs en nombres rationnels, mais seulement par à peu près; et si B avait 11 jetons blancs et 7 noirs, il serait encore un peu désavantagé; tandis que, au contraire, vous lui donnez moins de jetons blancs que de noirs.