Oeuvres complètes. Tome V. Correspondance 1664-1665
(1893)–Christiaan Huygens–No 1431.
| |
[pagina 401]
| |
door twe verscheijde wegen gemaakt, en zijnde geen nieuwe maar dezelfde daar ik de voornaamste quaestien in uw Tractaatjen van Rekening in spelen van geluk begrepen, door hadde gecalculeert, en selfde uitkompsten met UEdelheijt bevonden; dat ik geen correctie van mijne gevonden uitkompsten te gemoet heb gezien, maar wel in tegendeel hadde verwacht, dat UEdelheijt de foute van zijne verschillende uitkompsten, gelijk ik de mijne aangaande d' 1e quaestie hadde ontdekt en UEdelheijt bekent gemaakt, ook zouw hebben uitgevonden, en datwe alzo eens accorderende, met UEdelheijts antwoord een einde van deze dobbelrekeningen zouwden hebben gemaakt: Maar ik bekent, noit is mij iets meerder ontschooten, nochte onverwachter voorgekoomen, als UEdelheijts laatste vanden 7 dezer zijnde d'antwoord op deze mijne voorgaande, in welke dat ik zie dat UEdelheijt de moeite heeft genomen van zijne meditatien, die door eenige tusschenkomende tijd hem eenigzints ontschooten waaren, weder met lust te hervatten, en echter eindelijk dezelfde uitkompste van 207/343, in plaats van de mijne 9/245, wederom als vooren hadde bekoomen, voegende daar bij dat hij niet en twijfelde, of ik zouwde, mijn rekeninge naziende, zijne uitkompst waar bevinden. daarenboven dat zijn Edelheijt in mijne voorgestelde quaestie van Gelijkwaardig spel wel hadde bevonden dat zijne eerste gegeven facit, toevoegende aan B een gelijk getal van witte als swarte schijven, onrecht was, maar ook daar rentes et qui n'étaient pas nouvelles mais les mêmes par lesquelles j'avais calculé les principales questions comprises dans votre petit Traité de ‘Rekening in spelen van geluk’, et obtenu les mêmes résultats que vous), que je n'ai pas prévu de correction de mes résultats obtenus, mais que, bien au contraire, je m'étais attendu à ce que vous eussiez aussi découvert la faute de vos résultats différents, comme moi j'avais trouvé la mienne à l'égard de la 1re question et vous en avais fait part, et que, en nous accordant une fois, nous aurions fait par votre réponse une fin à ces calculs de jeux de hasard. Mais j'avoue que jamais rien ne m'a frappé plus, ni paru plus inattendu, que votre dernière du 7 courant qui est la réponse à ma précédente; dans laquelle je vois que vous vous êtes donné la peine de reprendre avec ardeur vos méditations, qui vous étaient plus on moins sorties de mémoire après quelque temps de relâche, et que pourtant à la fin vous avez trouvé le même résultat qu'auparavant de 207/343, au lieu du mien 9/245; vous y ajoutiez que vous ne doutiez aucunement que moi, en revisant mes calculs, je trouverais que votre résultat était le vrai. En outre, que dans la question de jeu équivalent, posée par moi, vous aviez bien trouvé que le premier résultat annoncé, de donner à B un même nombre de jetons blancs et de noirs, n'était pas juste, mais aussi que le mien, donnant | |
[pagina 402]
| |
nevens dat het mijne, gevende aan B 3 swarte tegens 2 witte, niet en was het rechte, maar dat zijn Edelheijt, stellende de rede der witte tot de swarte schijven als c tot d, kreeg deze aequatie 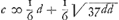 , zulx dat alhier de proportie der witte en swarte schijven in geen rationale getallen zouw konnen gegeven werden. Voorts, zo zijn Edelheijt de reden van de witte tot de swarte van A, die eerst werpt, met mij stelde te zijn als a tot b, en van B als c tot d, dat hij, om de kanzen gelijkwaardig te maaken, voor den generalen regel kreeg, deze aequatie cc ∞ - dc + aadc/ab + bb + add/b, in plaats van de mijne c ∞ ad/a + b. En eindelijk dat dit groote verschil, nevens 't geene ik hadde geschreven dat mijne quaestie van gelijkwaardigh spel, na mijne methode, lichter viel 't ontbinden als zijne Edelheijts eerste van kruis of munt, hem dede vast gelooven dat wij gantsch verscheijde wegen volghde; doch dat zijn Edelheijt zo wel zich vertrouwde op deze zijne bovenstaande regel, dat hij volgens dezelfde wel een kans zouwde derven waagen, zullende neemen de partije van A of B die men hem zouwde willen geven; maar, indien ik van gelijken aan zijn Edelheijt presenteerde met mijnen regel te willen doen, dat hij vande winst zich zouwde verzekert houwden: want nemende de partije van A, en mij die van B latende, zo zouwder, zo men aan A 10 witte en 1 swarte gaf, volgens mijn regel voor B koomen 10 witte en 11 swarte schijven; waar uit (voegt er zijn Edelheijt bij) het , zulx dat alhier de proportie der witte en swarte schijven in geen rationale getallen zouw konnen gegeven werden. Voorts, zo zijn Edelheijt de reden van de witte tot de swarte van A, die eerst werpt, met mij stelde te zijn als a tot b, en van B als c tot d, dat hij, om de kanzen gelijkwaardig te maaken, voor den generalen regel kreeg, deze aequatie cc ∞ - dc + aadc/ab + bb + add/b, in plaats van de mijne c ∞ ad/a + b. En eindelijk dat dit groote verschil, nevens 't geene ik hadde geschreven dat mijne quaestie van gelijkwaardigh spel, na mijne methode, lichter viel 't ontbinden als zijne Edelheijts eerste van kruis of munt, hem dede vast gelooven dat wij gantsch verscheijde wegen volghde; doch dat zijn Edelheijt zo wel zich vertrouwde op deze zijne bovenstaande regel, dat hij volgens dezelfde wel een kans zouwde derven waagen, zullende neemen de partije van A of B die men hem zouwde willen geven; maar, indien ik van gelijken aan zijn Edelheijt presenteerde met mijnen regel te willen doen, dat hij vande winst zich zouwde verzekert houwden: want nemende de partije van A, en mij die van B latende, zo zouwder, zo men aan A 10 witte en 1 swarte gaf, volgens mijn regel voor B koomen 10 witte en 11 swarte schijven; waar uit (voegt er zijn Edelheijt bij) het
à B 3 jetons noirs contre 2 blancs, n'était pas le vrai non plus; mais qu'en supposant la proportion des jetons blancs aux noirs comme de c à d, vous obteniez cette équation | |
[pagina 403]
| |
oogenschijnelijk blijkt, dat de kans van A beter is als die van B, ja noch beter alsmen de proportie der witte tot de swarte van A noch grooter steld: En dat A in deze van 10 tot 1, volgens den regel die zijn Edelheijt daar toe hadde, zouwde winnen 105/131 van 't geen ieder reijse ingezet wiert. Edoch evenwel dat zijn Edelheijt eenzelfde uitkompst met mij hadde gevonden op zijne laatste quaestie van kruis of munt om de kansen van A en B gelijk te maaken, te weeten dat ieder van eersten aan 2/3 van een ducaet zouw moeten inzetten. Wat meend UEdelheijt wel dat mijne gedachten waaren toen ik dit altemael voor d' 1e mael quam te lezen? want ik zag toen voort wel dat wij in geen van onze 4 quaestien, schoon d'uitkompsten der eerste en laatste wederzijts dezelfde waaren, noch kosten geoordeelt werden te accorderen, gemerkt de generale regel die UEdelheijt op diergelijke quaestien hadde, met de mijne niet en kost overeenkoomen, dewijl anders deze uwe twe uitkompsten 207/343, en deze laatste 105/131, hadden moeten accorderen met de mijne 9/245, en 0. maar dat waarschijnelijk deze overeenkompst in deze eerste en laatste quaestie was ontstaan uit de gelijkheijt der voorzegde letters a, b, c, d, die in d'andere ongelijk werden gestelt. (ajoutez-vous) il résulte évidemment que la chance de A est meilleure que celle de B, et qu'elle deviendrait encore meilleure, si l'on augmentait la proportion des jetons blancs aux noirs de A. Et que A, dans ce cas de 10 contre 1, suivant la règle que vous aviez pour cela, gagnerait 105/131 de ce qui chaque fois avait été mis. Mais que pourtant dans votre dernière question de croix ou pile, pour rendre égales les chances de A et de B, vous aviez trouvé le même résultat que moi à savoir que dès le commencement chacun devait mettre 2/3 d'un ducat. | |
[pagina 404]
| |
d'Eerste gedachten vielen op mijn zelfs, zouwd ik wel mij wederom hebben misrekent? daar is evenwel weijnig waarschijnelijkheijt, gemerkt ik alles door 2 verscheijde methode, en die mij de rechte uitkompsten hebben gegeven in andere quaestien, heb gerekent, en accorderende bevonden. Maar dat uw in d' 1e quaestie is gebeurt, kan uw dat niet wederom in d'andere ontmoeten? jaa'k: maar ik weet ook dat 't fondament van die fout bij nacht, uw al half slapende, geleijt is, en dat ik met veel wakkerder zinnen d'andere rekeningen heb bijgewoont. Zal dan d'Heer van Zuilichem, hebbende nu mijnen generalen regel, zijnde, gelijk andere, vandie natuur, dat alleen een exempel onder oneindige, en welke gemeenlijk licht is te determineren, haar valscheijt, zo ze niet goet is, kan aanwijsen, wederom op nieuws gemist hebben? Insonderheijt, daar hij zijn voorgaande raisonnementen bij na geheel vergeeten hebbende, de zaak met lust wederom hervat heeft? daar docht mij was noch minder waarschijnelijkheijt in; te meer als ik te gelijk daar bij voegde die bijzondere oefening en geslepenheid van gedachten die UEdelheijt omtrent de Speelen van Geluk boven anderen heeft bekoomen; en voor al zo ik met eenen quam te gedenken aan de rang die zijn Edelheijt onder de Geleerde, en d'uitstekentste Wiskonstenaars dezer eeuwe tegenwoordigh bekleet. Zeker, had ik toen gehouwden geweest een kansje op de bovenstaande conditien met UEdelheijt te waagen, ik had wel iets willen verliezen om ontslaagen te mogen wezen. ik zeg, wel iets, want toenmaels niet present hebbende Mes premières pensées tombèrent sur moi-même. Me serais-je peut-être de nouveau trompé dans mon calcul? Pourtant il y a peu de probabilité à cela, attendu que j'ai tout calculé par 2 méthodes différentes et qui m'avaient donné les vrais résultats dans d'autres questions, et que je les ai trouvées d'accord. Mais ce qui vous est arrivé dans la 1re question, cela ne peut-il pas se rencontrer dans les autres? oui vraiment; mais je sais aussi que le fondement de cette faute a été posé dans la nuit, pendant que vous dormiez à moitié, et que moi j'ai été présent à mes autres calculs avec des sens beaucoup plus éveillés. Est-ce que le seigneur de Zuilichem, - étant maintenant en possession de ma règle générale qui, comme d'autres, est de telle nature qu'un seul exemple parmi un nombre infini, et d'ordinaire un exemple facile à déterminer, peut indiquer sa fausseté quand elle n'est pas bonne, - se serait donc encore mépris? Et cela lorsque, ayant presque totalement oublié ses raisonnements antérieurs, il a de nouveau repris l'affaire avec ardeur? Voilà qui me semblait encore moins probable, en particulier si je tenais compte de cette habilité et finesse d'idées que vous avez acquises, à un plus haut degré que d'autres, en matière de jeux de hasard: et surtout quand en même temps je venais à considérer le rang que maintenant vous occupez parmi les savants et les plus excellents Mathématiciens de ce siècle. Certes, si alors j'avais été tenu à risquer une chance avec vous sous les conditions susdites, j'aurais bien voulu perdre quelque chose pour en être dispensé. Je dis: ‘quelque chose’, car n'ayant alors point | |
[pagina 405]
| |
mijne redenkavelingen, en niettemin noch zeer wel indagtig zijnde wat aandagt ik daar omtrent hadde gehat, zo vertrouwde ik noch al iet op mijne eigene krachten. Echter op die tijd liet ik de zaak in medio, en schorte mijn oordeel op tot nader examen. Ik stond reijsvaardigh om land-waert mijn vermaak wat te zoeken, en buiten 't krioel en gewoel der stedelingen mijn zinnen wat te vergaaren, die naast eenigen tijd door de rampzaligheden vande gemeene Staat zo vrij wat verstroijt en verwijdert waaren; ja een proef bij deze gelegenheijt op mijn zelfs te doen, hoever ik mij in deze bekommerlijke tijden, gerust, en buijten alle vrees, souw konnen stellen. Maar ik zie dat de grootste bergen leggen tusschen doen en zeggen. datter niet lichter is als de weg tot de gerustheijt uit te vinden, en niet swaarders als die te bewandelen:
Rex est qui metuit nihil,
Rex est quique cupit nihil.
'T zy zo, maar roeit de vrees en de begeerte eens uit. Hoc opus, hic labor est. Dit dan, mijn Heer, als mede eenige andere vermakelijke oefening, heeft mij een dagh 5 a 6 hier op 't land bezigh gehouwden, en niet toegelaaten, dat ik deze antwoord UEdelheijt eerder afvaardighde. Jn't herlezen dan van UEdelheijts brief zo zijn mijn gedachten 't eerst gevallen présents mes raisonnements, et néanmoins me souvenant fort bien de l'attention que j'y avais donnée, je me fiais quelque peu à mes propres forces. Pourtant je laissai à ce moment la chose in medio et suspendis mon opinion jusqu'à nouvel examen. J'étais près de me rendre à la campagne, pour y chercher quelque délassement et, hors du fourmillement et de l'agitation des citadins, rassembler mes idées, qui depuis quelque temps avaient été bien distraites et dispersées par les malheurs de la République; et même pour faire une expérience sur moi-même, savoir jusqu'à quel point, dans ces temps troublés, je pourrais me tenir tranquille et exempt de toute crainte. Mais je vois que les plus hautes montagnes se trouvent entre le faire et le dire, que rien n'est plus facile que de découvrir le chemin qui mène à la tranquillité et rien plus dissicile que de le suivre: | |
[pagina 406]
| |
op dat exempel waar uit UEdelheijt zeijt oogenschijnelijk te blijken, dat de kans van A (volgens mijn regel) beter is als die van B, en noch beter, alsmen de proportie der witte tot de swarte van A noch grooter steld; welke kans nochtans volgens den eysch gelijk most zijn. Zulx dat d'ongoetheyt van mijnen regel hier dan oogenschijnelijk zoude getoont weezen. Toen ik dit een weijnig had nagedagt, en niet konnende vinden dat zijn Edelheijt hier in gelijk hadde, maar wel recht in tegendeel, namentlijk, dat de goetheijt van mijnen regel zelfs oogenschijnelijk in dit exempel, en ook zelfs noch beter als men de proportie der witte tot de swarte schijven van A noch grooter nam, niet alleenlijk bleek maar ook demonstrativelijk d'ongoetheijt van zijn Edelheijts regel daar in uitstak, dat deed mij wederom wat beter moet krijgen, en mijn kans willigen, ook zowel, dat wij hadden moeten speelen na onse regels, ik 't spel egael na de mijne, maar groote winst na d' uwe, zouw gerekent hebben jndien UEdelheijt de kans van A, ik die van B hadde aangenoomen. Zulx dat ik op't ouwde geloof aan, (want op die tijd had ik mijn rekeninge en ratiocinatien omtrent dezelfde, noch niet overzien,) noch wel 2 kansen op uwe gepreesenteerde conditien had durven en willen waagen. Nu dat ik bij de kans van B, aan UEdelheijt die van A latende, voordeel zouw hebben zowe na zijn Edelheijts regel speelde, is notoir, zo men alleenlijk let, datter noch bij A noch B kan verlooren werden ten zij A eerst een ducaet heeft ingezet: Want zo A voor d' 1e mael trekkende een witte schijf aantreft, zo is het spel uitGa naar einda), en niemand verliest of wint daar iets bij, maar elk blijft in zijn geheel, ge- il suit evidemment, dites-vous, que la chance de A (suivant ma règle) est meilleure que celle de B, et encore plus quand on suppose encore plus grande la proportion des jetons blancs aux noirs de A, laquelle chance pourtant devrait être égale d'après les conditions. De sorte qu'ainsi serait démontrée à l'évidence la défectuosité de ma règle. En y réfléchistant quelque peu, je ne pus trouver que vous aviez raison; bien au contraire, non seulement la justesse de ma règle apparaissait à l'évidence dans cet exemple, et même encore plus quand on prenait la proportion des jetons blancs aux noirs de A encore plus grande, mais aussi la défectuosité de votre règle y ressortait d'une manière démonstrative. Cela me rendit un peu de courage et me fit trouver ma chance meilleure, à tel point que, si nous avions dû jouer suivant nos règles, j'aurais jugé la partie égale suivant ma règle, mais très avantageuse pour moi suivant la vôtre, si vous aviez pris la chance de A, moi celle de B. De sorte que suivant ma foi ancienne (car à cette heure je n'avais pas encore revu mes calculs et mes raisonnements sur cette question) j'aurais bien osé et voulu risquer 2 chances aux conditions offertes par vous. | |
[pagina 407]
| |
merkt er in 't begin van 't spel niets is ingezet, en datter gelijk-spel wert gepraesupponeert, dat is, dat de conditien eer 't spel is begonnen van A zo goet zijn als die van B, en in tegendeel die van B als die van A: Zo dat het dan eveneens is of A eerst trekt, dan of hij 1 ducaet inzet en B laat trekken. Jndien dan nu B meerder of maar gelijke kans heeft tot deze ducaet te trekken als tot een nieuwe bij te zetten, ofte dat het zelfde is, meerder of maar evenveel witte als swarte schijven heeft, zo zal immers nootzaakelijk de conditie van B beter moeten zijn, en noch zoveel te beter als B meerder witte als swarte heeft, dewijl de witte het spel doen winnen. Want laatenwe aan B maar eens toevoegen evensoveel witte als swarte schijven; dewijl nu A een ducaet heeft ingezet, en dat B moet trekken, zo ist notoir, na gelijk-spel dat alsdan B met het trekken van een swarte schijf nootzaaklijk een ducaet moet verliezen, die A dan nevens de zijne zoude na zich haalen; maar zo nu beijde deze op't trekken van een swarte schijf blijven staan, zo kan A voor de 2e mael trekkende, en een witte aantreffende, daar mede geen voordeel doen, maar alleenlijk genieten, 'tgeen hem alreets na gelijk-spel toequam, maar een swarte aantreffende, moet hij weder een ducaet bijzetten, zo dat B dan niet alleenlijk een trek behout van gelijke kans op deze nieuwe inleg van A, maar ook op de voorgaande 2 ducaten die aan A alreets toequaamen; zulx dat, zo B komt een witte te trekken hij alreets 2 ducaten meer als na gelijk-spel zou winnen, zo een swarte, komt hij alleenlijk een ducaet, die aan A nu al toekomt, bij te zetten. en ce cas, mais chacun reste dans son entier, attendu qu'au commencement du jeu rien n'a été mis, et que l'on a supposé jeu égal: c'est-à-dire, supposé qu'avant le commencement du jeu les conditions de A soient aussi bonnes que celles de B, et réciproquement celles de B que celles de A. De sorte qu'il est indifférent que A tire le premier, ou qu'il mette un ducat et laisse tirer B. Si maintenant B a plus grande chance, ou seulement chance égale, de tirer ce ducat que d'en mettre un nouveau, ou, ce qui revient au même, s'il a plus, ou seulement autant, de jetons blancs que de noirs, alors certes la condition de B devra nécessairement être la meilleure, et d'autant meilleure, que B a plus de jetons blancs en proportion des noirs, puisque les blancs font gagner la partie. Car, donnons seulement à B autant de jetons blancs que de noirs; comme A a mis un ducat et que B doit tirer, il est manifeste, à jeu égal, que B en tirant un jeton noir doit nécessairement perdre un ducat, que A empocherait alors avec le sien; mais si, après le tir d'un jeton noir, ces deux ducats restent au jeu, A en tirant la 2e fois, et tombant sur un jeton blanc, n'en aura pas de profit, mais jouira seulement de ce qui lui revenait déjà suivant le jeu égal; mais amenant un jeton noir, il doit de nouveau mettre un ducat, de sorte que B non seulement conserve un tour de chance égale sur cette nouvelle mise de A, mais encore sur les 2 ducats qui déjà appartenaient à A; ce qui fait que si B vient à tirer un jeton blanc, il gagnerait déjà 2 ducats de plus que suivant le jeu égal, mais s'il tire un jeton noir, il lui faut seulement mettre un ducat, qui maintenant déjà revient à A. | |
[pagina 408]
| |
Waar uit dan blijkt dat B noch altijt zou behouden eenige portie in 't geen hij na Gelijkspel alreets verlooren had, en derhalven zoveel advantage daar bij hebben. Hoeveel te meerder advantage heeft B dan zo hem meerder witte als swarte schijven toegevoeght werden. Zo men dan nu aan A geeft 10 witte en 1 swarte schijf, zo zullender voor B (volgens UEdelheijts regeltje) meer als 9 mael zoveel witte als swarte koomen, en zo men aan A geeft 100 witte en 1 swarte, zo zullender voor B meer als 99 mael zoveel witte als swarte koomen, en zo voorts zal de proportie der witte tot de swarte schijven van B noch groter werden zo men de proportie der witte tot de swarte van A noch grooter stelt, en derhalven de kans van B om te winnen ook geduurigh toeneemen. Zulx dat hier uit dan demonstrativelijk blijkt dat UEdelheijts bovenstaande regel niet goet kan zijn. Voorts dat ook uit dezelfde exempelen oogenschijnelijk de goetheijt van mijnen regel gezien wort, blijkt hier uit, dat B voor eerst na dezelfde noijt soveel witte als swarte schijven kan hebben, en dan voorts uit de nette proportie die'er in d'exempels wort waargenoomen, die ons, gelijk ook de reden mebrengt, toonen, dat, hoe de proportie van de witte tot de swarte schijven van A grooter is, hoe die van de witte tot de swarte van B gelijker wort: Want zo men aan A geeft 10 witte en 1 swarte, zo koomender voor B 10 witte en 11 swarte; zo men aan A geeft 100 witte en 1 swarte, zo koomender voor B 100 witte en 101 swarte; zo men aan A geeft 1000 witte en 1 swarte, zo koomender voor B 1000 witte en 1001 D'où il résulte que B garderait encore toujours quelque portion de ce qu'il avait déjà perdu d'après le jeu égal, et que, par conséquent, il y aurait avantage d'autant. Combien plus d'avantage aurait donc B, si on lui donnait plus de jetons blancs que de noirs. | |
[pagina 409]
| |
swarte. En dat nu dit de reden ook leert, wort licht gezien, zo men alleenlijk 't voorgaande gedenkt, namentlijk datter niet gewonnen noch verloren kan werden ten zij A eerst een ducaet inzet; want B daar na trekkende moet zoveel te nader koomen aande gelijke kans om te winnen of een ducaet in te zetten, als A grooter kans heeft, B mis-trekkende, om te winnen. Wat nu ook d'andere quaestie belangt daar UEdelheijt voor 't facit geeft 207/343, daar zal hij ook klaar zien in gemist te hebben, zo hij alleenlijk maar eens gelieft te rekenen wat A van B souw winnen blijvende alle dezelfde conditien der quaestie uitgenoomen alleen dat A niet gehouwden zal zijn oit iets in te leggen, maar alleen B, die dan alleen ook maar zal konnen verliezen. En een goede calculatie zal zijn Edelheijt als dan toonen, dat zelfs de conditie van A in deze gelegentheit nu A zelfs niets kan verliezen, en echter B eveneens verbonden blijft, geen 207/343 van een ducaet waart is, maar niet meer als 12/49. Insgelijx in dit laatste exempel daar A 10 witte en 1 swarte schijf heeft, en B 10 witte en 11 swarte, en daar volgens den regel die UEdelheijt daar toeheeft, A zouwde winnen 105/131 van 't geen ieder reijse ingezet is, zouwde A maar konnen winnen van B, indien A, facilement que la raison nous apprend la même chose, si seulement on se souvient de ce qui précède, savoir, qu'il ne peut y avoir ni gain ni perte avant que A n'ait mis d'abord un ducat; car B, tirant ensuite, doit approcher d'autant plus de la chance égale de gagner ou de mettre un ducat, que A a une chance plus grande de gagner, lorsque B tire à faux. | |
[pagina 410]
| |
gelijk als vooren, zelfs niet gehouwden zouw zijn oit iets in te leggen, 21/440 van 't geen ieder reijse ingezet moet werden; en dienvolgens ist notoir dat A noch minder moet winnen indien hij daar nevens ook gehouwden zij in te zetten, dewijl dit aan A geen voordeel maar alleen verlies kan aanbrengen. Dewijl nu UEdelheijts generalen Regel, die op deze laatste past, ook nootzaaklijk applicabel moet zijn op de voorgaande, als mede op UEdelheijts eerste quaestie van kruis of munt, zo blijkt klaarlijk datwe na dezelfde, in't facit van de eerste, en bij gevolg ook vande laatste quaestie, die daar uit met zeer weijnigh verandering vloeit, bij geval ook maar eenselvige uitkompsten konnen vinden. En nu geloof ik is UEdelheijt noch al zo zeer verwondert als ik was; want na ik merk, zo en verwachte hij geene correctie op zijne correctien, schoon hij het contrarie in't einde van zijn brief, doch al lacchende, zeide. En zal nu wel-licht met mij wel wederom op nieuws eens mees-muijlen, ziende datwe zoveel brieven nopende deze dobbel-quaestien over en weer gewisselt hebben, en datwe noch niet verder geraakt, maar veel eer terug gegaan zijn, gemerkt er nu niet eene quaestie overgebleven is, in welke wij ons konnen verzekeren volkomentlijk met den anderen te accorderen. Maar mij dunkt evenwel dat het nu tijt begint te worden om een eind van deze zaak te maaken die ruim lang genoeg geduurt heeft. de kortste wegh daar toe zal dan zijn, dat ik UEdelheijt toone een van chose, pourrait seulement gagner de B 21/440 de ce qui chaque fois doit être mis; et par suite il est manifeste que A devra gagner encore moins, si, en outre, il est tenu à mettre, parce que cela ne peut apporter du gain à A, mais seulement de la perte. | |
[pagina 411]
| |
mijne Methode, waar door ik alle onze voorgestelde dobbel-quaestien, welke in ordre de volgende 4 zijn, hebbe gesolveert, en waar door ik met eenen te gelijk zal konnen aanwijsen 't geen ik hier boven aangaande UEdelheijts uitkompsten 207/343, en 105/131 hebbe gezeijt. | |
1e Quaestie bij UEdelheijt voorgestelt.A en B werpen op met beurten kruis of munt op conditie dat die munt werpt een ducaet zal inzetten, maar die kruis werpt, zal alles strijken dat ingezet is. En A werpt eerst zijnde noch niets ingezet. de vrage is, hoeveel dat A verliest als hij dit spel aangaet, ofte hoeveel hij aan B zouwde konnen geven om daar uit te mogen scheijden? Tot antwoord hebben wij hier op wederzijts gegeven dat A hier bij souwde verliesen 4/27 van 1 ducaet. | |
2e Quaestie bij mij UEdelheijt voorgestelt.A en B trekken blindelinx bij beurten, A altijt uit 3 schijven 1, van welke twe wit zijn en een swart; B insgelijx altijt uit een zeker getal van witte en swarte schijven waar van de ratio onveranderlijk blijft; op conditie, dat die een Méthodes, par laquelle j'ai résolu toutes les questions de jeux de hasard que nous avons proposées, qui dans leur ordre sont les 4 suivantes; et ainsi je pourrai démontrer en même temps ce que j'ai dit ci-dessus à l'égard de vos résultats 207/343 et 105/131. | |
1e Question proposée par vous.A et B jettent à tour de rôle à croix ou pile, sous condition qùe celui qui jette pile, mettra un ducat, mais que celui qui jette croix râflera tout ce qui a été mis. Et A jette le premier, alors que rien encore n'a été mis. On demande, quel est le désavantage de A lorsqu'il engage cette partie, ou combien il devrait donner à B pour pouvoir en finir? | |
2e Question proposée par moi.A et B tirent à tour de rôle à l'aveuglette, A toujours un de 3 jetons, desquels deux sont blancs et un noir; B également toujours d'un certain nombre de jetons blancs et noirs, dont la ratio reste invariable; sous condition que celui qui tire un jeton blanc | |
[pagina 412]
| |
witte schijf trekt alles watter instaet genieten zal, maar die in tegendeel een swarte aantreft, altijt een ducaet zal bijzetten, en A zal eerst trekken zijnde noch niets ingezet. de vrage is, zomen de conditie wederzijts gelijk-waardigh wil hebben, zulx datter, als A zal beginnen te trekken geen voordeel bij d'een noch d'ander zij, wat ratio datter zal moeten wezen tusschen de voorseijde witte en swarte schijven? Deze begeerde ratio zeijt UEdelheijt te zijn als c tot d, zijnde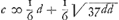 ; ofte generalijk cc ∞ - dc + aadc/ab + bb + add/b zomen de reden der witte tot de swarte van A, die eerst werptGa naar voetnoot4), stelt te zijn als a tot b. En ik stelze als 2 tot 3, ofte generalijk c ∞ ad/a + b. ; ofte generalijk cc ∞ - dc + aadc/ab + bb + add/b zomen de reden der witte tot de swarte van A, die eerst werptGa naar voetnoot4), stelt te zijn als a tot b. En ik stelze als 2 tot 3, ofte generalijk c ∞ ad/a + b.
| |
3e Quaestie bij UEdelheijt voorgestelt.Jndien in deze twede quaestie B 2 swarte en 1 witte schijve heeft, de rest gestelt als daar; hoeveel wint of verliest A dan? UEdelheijt zegt dat A alsdan zouw winnen 207/343 van een ducaet, en ik niet meer als 9/245. jouira de tout ce qui a été mis, mais que celui au contraire qui amène un jeton noir, ajoutera toujours un ducat; et A tirera le premier, lorsque rien n'a encore été mis. Si maintenant on veut avoir la condition équivalente de part et d'autre, de telle sorte que, A commençant à tirer, il n'y ait pas d'avantage pour l'un ni pour l'autre, on demande quelle ratio il devra exister entre les susdits jetons blancs et noirs? | |
3e Question proposée par vous.Lorsque dans cette deuxième question B a 2 jetons noirs et 1 jeton blanc, le reste étant posé comme précédemment; combien est-ce que A gagne ou perd alors? Vous dites que A gagnerait alors 207/343 d'un ducat, et moi pas plus de 9/245. | |
[pagina 413]
| |
4e Quaestie bij UEdelheijt voorgestelt.A en B werpen op met beurten kruis of munt, op conditie dat die munt werpt een ducaet zal inzetten, maar die kruis werpt zal alles strijken dat ingezet is; en A zal eerst werpen. de vrage is, hoeveel dat A en B zouwden behooren van eersten aan in te zetten, te weten ieder een gelijke zomme, om te maaken dat de conditien van A en B gelijk wierden? Hier op geven wij wederzijts een gelijke solutie, namentlijk 2/3 van een ducaat voor ieders inlegh apart. Om dan UEdelheijt met eenen te toonen dat mijn voorgestelde quaestie van gelijk-spel lichter valt na mijn methode te calculeren als UEdelheijts eerste van kruis of munt, gelijk ik gestelt hadde, zo zal ik van dezelve beginnen, stellende de ratio der witte en swarte schijven zo van A als B, gelijk boven, en noemende, 't geen op 't trekken van een swarte schijf ingezet moet werden r. Jk considereer dan voor 1. Datter wederzijts in dit Gelijk-Spel noch gewonnen noch verlooren kan worden ten zij A, die eerst werpt, koome een swarte schijf te trekkenGa naar eindb), en alzo r in te zetten: en derhalven dat het eveneens is of A eerst werptGa naar voetnoot6), dan of | |
4e Question proposée par vous.A et B jettent à tour de rôle à croix ou pile, sous condition que celui qui jette pile mettra un ducat, mais que celui qui jette croix râflera tout ce qui a été mis; et A jettera le premier. On demande, combien A et B devraient mettre en commençant, c'est-à-dire chacun une somme égale, pour faire que les conditions de A et de B deviennent égales? | |
[pagina 414]
| |
hij r inzet, en B laat werpen. Ten 2de zo reken ik wat B uit Aas, en in tegendeel A uit Bees possible inlegh toekomt. dat is, wat Bees conditie waart zouw zijn zo A alleen verpligt was op 't trekken van een swarte schijf, r in te zetten; en wederom in tegendeel wat Aas conditie waart zou zijn, zo B alleen tot het inzetten verplicht was. Ten 3e considereer ik dat deze waardens aan malkander gelijk moeten zijn. En eindelijk ten 4den, dewijl deze wederzijtsche waardens uitgedrukt werden door twee oneindige progressien waar van de ratio der termen eenzelvig is, dat dan nootzaaklijk, om d'evengrootheijt haarder zommen, de wederzijtsche eerste termen aan malkander ook gelijk moeten zijn. Zulx dat
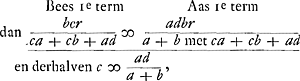 gelijk ik voor 't generale facit hadde gegeven; ofte toegepast tot dit casus, alwaar a is gelijk 2, b ∞ 1, zo krijgt men c ∞ 2d/3 ofte 3 c ∞ 2 d, en derhalve ook voor de begeerde ratio der witte en swarte schijven van B als boven. Voorts om UEdelheijts 1e quaestie generaalijk te solveren zo moet ik, na die methodus, considereren voor 1 de zom van beijde deze gezeijde progressien, en dan premier, ou bien qu'il mette r et laisse tirer B. 2o Je calcule ce qui revient à B de la mise possible de A, et réciproquement ce qui revient à A de la mise possible de B; c'est-à-dire ce que vaudrait la condition de B, si A seul était obligé de mettre r en tirant un jeton noir; et encore réciproquement ce que vaudrait la condition de A, si B seul était obligé de mettre. 3o Je considère que ces valeurs doivent être égales entre elles. Et enfin 4o, comme ces valeurs de part et d'autre sont exprimées par deux progressions infinies, dont la ratio des termes est de même forme, qu'il faut nécessairement, à cause de l'égalité de leurs sommes, que leur premiers termes de part et d'autre soient égaux. De sorte que | |
[pagina 415]
| |
ten anderen noch d' 1e werp van A voorzoveel hij kruijs kan werpen, en 't spel daar mede uitmaken. dat is, den geene die voordeel bij 't spel hadde, zoveel voordeels doen verliezen. en eindelijk, dat, noemende x de beter of slimmer kans van B, dat deze waarde van d' 1e werp van A voorsoveel hij kruis kan werpen, plus 't geen hem uit de possible inleg van B zouw toekoomen, gezamentlijk afgetrokken van 't geen B uit de possible inleg van A zou toekomen, evengelijk moet zijn aan x, dat is
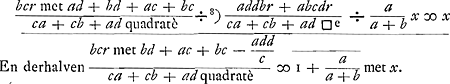 Ga naar voetnoot8) Dit is dan mijnen generaalen RegelGa naar eindc) op zodanige quaestien als UEdelheijts 1e en 3e, zulx dat zomen a, b, c, d elk stelt ∞ 1, volgens d'inhout van d' 1e, zo krijgt men 2/9 r ∞ 3/2 x en x ∞ 4/27 r. Jnsgelijx, zomen stelt a ∞ 2, b ∞ 1, c ∞ 1, d ∞ 2, volgens d' inhout van de 3e, zo krijgt men ÷ 3/49 r ∞ 5/3 x, en x ∞ ÷ lieu encore le 1er coup de A, en tant qu'il peut jeter croix, et finir ainsi le jeu, c'est-à-dire faire perdre à celui qui avait avantage à ce jeu, tout cet avantage; et enfin que, si l'on nomme x la chance meilleure ou pire de B, cette valeur du 1er coup de A, pour autant qu'il peut jeter croix, plus ce qui lui pourrait revenir de la mise possible de B, étant soustraits ensemble de ce qui reviendrait à B de la mise possible de A, la différence doit être égale à x, c'est-à-dire | |
[pagina 416]
| |
9/245r. Zulx dat volgens d' 1e quaestie B zoude winnen 4/27 van een ducaet, en volgens d' andere 9/245 van een ducaet verliezen. gelijkwe ook UEdelheijt hadden geschreven. En nu kan hier ook met eenen gezien werden de waarheijt van 't geen ik hier vooren aangaande uw Edelheijts gevonden uitkompste 207/343 en 105/131 gesegt hebbe: Want zo men alles considereert als in de quaestien, uitgenoomen dat A niet gehouwden zal zijn iets in te leggen op 't trekken van een swarte schijf, zo zalmen bevinden dat dit aan A alleen zal waart zijn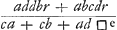 , evensoveel als hier boven gerekent is dat A uit de possible inleg van B zouw toekoomen, twelk dan in dit casus van de 3e quaestie niet meer is als 12/49 r, ofte 12/49 van een ducaet. En zomen stelt a ∞ 10, b ∞ 1, c ∞ 10, d ∞ 11, gelijk in 't ander casus, daar UEdelheijt volgens zijnen regel vind dat A zouwde winnen 105/131 van een ducaet, daar zou 't aan A niet meer waart zijn als 21/440 r, alles accorderende met 't geene wij hier vooren gezeijt hebben. , evensoveel als hier boven gerekent is dat A uit de possible inleg van B zouw toekoomen, twelk dan in dit casus van de 3e quaestie niet meer is als 12/49 r, ofte 12/49 van een ducaet. En zomen stelt a ∞ 10, b ∞ 1, c ∞ 10, d ∞ 11, gelijk in 't ander casus, daar UEdelheijt volgens zijnen regel vind dat A zouwde winnen 105/131 van een ducaet, daar zou 't aan A niet meer waart zijn als 21/440 r, alles accorderende met 't geene wij hier vooren gezeijt hebben.
De sorte que suivant la 1e question B gagnerait 4/27 d'un ducat, et que suivant l'autre il perdrait 9/245 d'un ducat; comme je vous l'avais écrit. | |
[pagina 417]
| |
Eindelijk en ten laatsten wat belangt de 4e quaestie, die wort zo licht gehaalt uit deze voorgaande, dattet onnodigh is die 25 letters, die ik 'er omtrent toegebruik, hier bij te voegen. Wij zullen derhalven hier mede eindigen, en gelooven, dat w' ook 't eind van onze dobbel-quaestien hier mede sullen hebben bekoomen. ende blijven
Mijn Heer VEdelheijts dienstwilligen dienaar I. Hudden.
Den 20 Julij 1665 op't landt even buijten de rook van Amsterdam. En dernier lieu et finalement, pour ce qui regarde la 4e question, on la déduit si aisément de cette précédente qu'il n'est pas nécessaire d'ajouter ici les 25 lettres que j'y emploie. Par conséquent nous terminerons ici, et croirons qu'ainsi nous sommes aussi parvenus au terme de nos questions de jeux de hasard. Je reste |
|


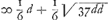 ; ou généralement cc ∞ - dc + aadc/ab + bb + add/b, lorsqu'on suppose que la raison des jetons blancs aux noirs de A, qui jette
; ou généralement cc ∞ - dc + aadc/ab + bb + add/b, lorsqu'on suppose que la raison des jetons blancs aux noirs de A, qui jette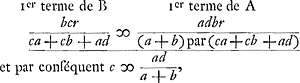
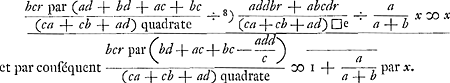
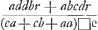 , tout autant que, d'après le calcul ci-dessus, il reviendrait à A de la mise possible de B, ce qui dans ce cas de la 3e question n'est pas plus de 12/49 r, ou 12/49 d'un ducat. Et lorsqu'on prend a ∞ 10, b ∞ 1, c ∞ 10, et d ∞ 11, comme dans l'autre cas, où vous trouvez suivant votre règle que A gagnerait 105/131 d'un ducat, cela ne vaudra à A pas plus de 21/440 r, le tout en accord avec ce que nous avons dit plus haut.
, tout autant que, d'après le calcul ci-dessus, il reviendrait à A de la mise possible de B, ce qui dans ce cas de la 3e question n'est pas plus de 12/49 r, ou 12/49 d'un ducat. Et lorsqu'on prend a ∞ 10, b ∞ 1, c ∞ 10, et d ∞ 11, comme dans l'autre cas, où vous trouvez suivant votre règle que A gagnerait 105/131 d'un ducat, cela ne vaudra à A pas plus de 21/440 r, le tout en accord avec ce que nous avons dit plus haut.