Oeuvres complètes. Tome IV. Correspondance 1662-1663

[p. 138]

N^o 1017.
Christiaan Huygens à [P. Petit].
[25 mai 1662].
Appendice au No. 1016.

La minute et la copis se trouvent à Leiden, coll. Huygens

A Monsieur Petit, Sur l'Aequation des jours.

Si le soleil au lieu d'aller par l'Ecliptique suivoit tousjours l'aequateur, et que dans cettuicy il cheminast d'un mouvement egal le parcourant dans le mesme espace de temps qu'il acheve maintenant l'Ecliptique, c'est a dire dans le temps d'un an tropique, il est certain que tous les jours d'un midy a l'autre seroient necessairement egaux, et que chacun d'eux seroit d'une conversion entiere de l'equateur et encore d'une partie de l'aequateur que le soleil y avanceroit journellement, qui seroit de 59′ 8″ 20‴. puis que d'autant est son mouvement moyen dans l'Ecliptique de sorte que le temps d'un jour mediocre, et la juste mesure de 24 heures, est celuy dans lequel passent les 360 de l'equateur avec 59′ 8″ 20‴. On n'auroit donc pas besoin alors d'aucune aequation du temps et l'horologe estant une fois ajustée a la longueur des tels jours moyens ou mediocres s'accorderoit perpetuellement avec les quadrants. Mais le mouvement du soleil estant dans l'Ecliptique qui est oblique a l'equateur, et ce mouvement estant de plus inegal a raison de l'excentricitè du grand orbe, c'est pour ces deux causes que l'on y trouve presque tousjours de la difference et qu'on ne scauroit examiner la justesse des horologes par le moyen des quadrants qu'en se servant de la dite aequation pour laquelle je vous ay donnè une table¹⁾ avec la methode²⁾ pour en user. Mais pour vous faire veoir le fondement du calcul de cette table et comment on la construit facilement par le moyen des Ephemerides. prenons par exemple qu'au 10^e d'avril 1660 le soleil estant au meridien de Paris, en mesme instant l'horologe ajustée au temps mediocre dessus dit, montre aussi midy; et que je veuille scavoir si 10 jours apres a scavoir le 20 avril il sera encore midy a l'horologe quand il le sera au soleil ou quelle sera la difference.

Soit de la sphere ACBD les poles A, B; CD l'equateur, EF l'ecliptique, le principe d'Aries en G. Et que H soit le lieu du ☉ à midy du 10 avril. H est donc selon les Ephemerides d'Eichstadt. le 21^o 20′ 45″, de ♈, dont l'ascension droite

1) Voir la pièce N^o. 979.

2) Voir la pièce N^o. 978.

[p. 139]

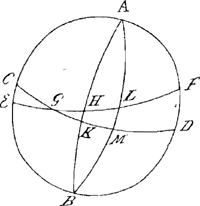GK est de 19^o 42′, et le point K est au meridien en mesme temps que H. Le 20^me au midy le soleil, selon les mesmes Ephemerides, sera parvenu au 1^o. 5′. 15″. de ♉ qui soit L, et son ascension droite GM sera de 28^o. 56′. Et il sera midy lors que le point L de l'ecliptique et ensemble le point M de l'equateur seront au meridien de Paris, de sorte que la durée des jours apparents entre le midy du 10 avril et le midy du 20 du mesme mois est à 10 conversions entieres de l'equateur et encore de l'arc KM. Or si l'arc KM, que l'on trouve en ostant l'ascension droite GK de GM, estoit de 10 fois 59′ 8″ 20‴ ou 9. 51′ 11″³⁾, ce seroit alors autant comme si le soleil avoit cheminè dans l'equateur et de son mouvement moyen, et partant le temps entre les dit deux midis seroit egal a 10 jours du temps moyen, suivant ce que j'ay dit au commencement. Mais l'arc KM n'est icy que de 9^o. 14′. de sorte que la difference est de 37′. Et partant le lieu du soleil M sera parvenu au meridien de Paris auparavant que l'horologe marque midy, et la difference du temps sera d'autant qu'il en faut pour que les dites [37′?] passent le meridien, c'est a dire de 2 minutes 28 secondes, car par la regle de proportion puis que les 360 degres et 59′. 8″. 20‴ de l'equateur (en omettant ces 59′. 8″. 20‴ parce qu'ils ne sont pas consideres) passent en 24 heures, les 37′0 passeront en 2′. 28″ 5. Ces minutes et secondes donc sont l'equation qu'il faut oster du temps apparent pour avoir l'heure du temps moyen le 20 avril 1660, lors qu'on a posè le midy du 10 jour du mesme avril pour epoche ou commun commencement de l'un et l'autre temps. Et suivant cette methode l'on peut sur la mesme epoche supputer l'aequation qui convient a tous les jours de l'année pour en composer une table.

Or il faut scavoir que les nombres de cette table ayant pour epoche le 10 d'avril susdit, seroient autres que de celle que vous avez de moy, qui a pour Epoche le 10 de Fevrier mais en effect les equations que l'on tireroit de l'une et l'autre seroient toutes les mesmes. Comme si par cette derniere je veux enquerir combien l'horologe doit differer du soleil au midy du 20 d'avril, ayant estè accordée avec luy le midy du 10 avril, il faut suivant la regle que j'ay donnée avec la table oster du nombre appartenant au 20 avril, qui est 16′, 34″, le nombre appartenant au 10 avril, qui est 14′, 6″, dont il reste 2′ 28″ de temps que le midy apparent devancera celuy de l'horologe parce que le nombre du 20 avril est plus grand que celuy du 10. Ou vous voyez que c'est la mesme equation que nous avions trouvée cy dessus. N'importe quelle soit l'Epoche que regardent les nombres de la Table puis que necessairement les mesmes aequations en provienent. J'ay pris

3) Lisez: 9^o 51′ 23″.

[p. 140]

toutefois dans la miene pour Epoche le 10 febrier (pouvant encore prendre le 1 de novembre) parce que en commencant de quelque autre jour il eust fallu distinguer dans la table les aequations additives et subtractives, ce qui en eust rendu l'usage moins facile. Elle pourra servir assez longues annees sans faute notable, parce que le changement de l'apogee du soleil qui seul la peut alterer est tres lent a scavoir d'environ 1 degrè en 60 ans. Au reste cette maniere d'aequation n'est autre que celle qu'a enseignè Ptolemée et apres luy Copernicus et plusieurs autres, servant à comparer ensemble quelque espace du temps apparent avec le temps egal, et assurement c'est l'unique et la veritable.

Quelques uns toutefois se sont imaginez, comme nostre amy Monsieur Bouillaut dans son Astronomia Philolaica⁴⁾ qu'il falloit une aequation pour reduire le moment du temps apparent au temps moyen, et ceux la sans avoir egard a l'Epoché veulent qu'a chasque jour de l'année conviene une equation certaine, les quels pour cela trouveroient estrange que l'une table auroit d'autres nombres que l'autre. Mais leur aequation pretendue est sans aucun fondement et ne signifie rien, car de quelque moment que l'on veuille l'on peut commencer a conter ensemble le temps egal et apparent comme d'un commun principe, et ils ne peuvent differer l'un de l'autre que dans quelque espace de temps. Ainsi nous venons de veoir que les 10 jours du temps apparent depuis le midy du 10 avril jusqu'au midy du 20 avril sont plus courts que 10 jours du temps egal ou mediocre; mais qui demanderoit au midy apparent du 10 Avril combien il y a encore au midy du temps moyen, ou de combien il est passè, je dirois que sa demande est ridicule, si ce n'est qu'il ait egard a quelque epoche auparavant d'ou l'on suppose que le compte du temps moyen et du temps apparent ait pris commencement. et selon que l'on posera cette epoche, le midy du temps moyen suivra ou devancera le midy du temps apparent, ou se rencontrera justement en mesme temps.

Devant que sinir je vous diray encore icy les remarques que l'on peut faire en prenant garde dans la table des aequations, comment les nombres y croissent et diminuent. C'est premierement que la moyene ou mediocre longueur des jours apparents revient quatre fois l'an, à scavoir vers le 10 Fevrier, le 15 May, le 25 Juillet et le 1 Novembre ce qui est evident parce qu'en prenant quel qu'un de ces jours la pour epoche, il n'y a point d'equation ou tres petite à faire les 2 ou 3 jours suivants. En quoy pourtant il y en a qui se sont trompez croyants que cette mediocritè des jours ne revient que deux fois l'annee.

Depuis le 10 Fevrier jusqu'au 15 May les jours apparents sont plus courts chacun que les mediocres. et que les plus courts vers le dernier de Mars.

Qu'au contraire depuis le 15 May jusqu'au 25 Juillet les jours apparents sont plus longs chacun que les jours mediocres et que les plus longs vers le 20 Juin. que

4) Voir l'ouvrage cité dans la Lettre N^o. 156, note 7.

[p. 141]

derechef depuis le 25 Juillet jusqu'au 1 Novembre les jours apparents sont plus courts que les mediocres, et que les plus courts vers le 18 Septembre.

Et qu'au contraire du 1 Novembre au 10 Fevrier les apparents surpassent les mediocres, et que les plus longs sont vers le 24 Decembre qui sont aussi les plus longs de toute l'année, excedant un jour mediocre de 31 secondes.

Ainsi ayant accordè l'horologe avec le soleil au midy du 10 Fevrier il monstrera le 1 Novembre 11 heures 28′. 5″. quand le soleil sera desia au meridien, ce qui fait veoir que les jours apparents de cet espace n'egalent pas autant de jours mediocres, mais qu'ils sont plus courts de 31′. 55″. Mais ayant accordè l'horologe avec le soleil le 1 Novembre il marquera au 10 Fevrier 31′. 55″ apres midy quand le soleil sera au midy. d'ou il s'ensuit que les jours apparents du 1 Novembre jusqu'au 10 Fevrier sont plus longs de 31′. 55″. qu'autant de jours mediocres.

Je pourois encore remarquer icy l'erreur de Ptolemee, de Copernicus et d'autres qui les suivent qui, considerants ces deux termes entre les quels il y a la plus grande difference des jours apparents aux mediocres, et que les apparens du dernier espace surpassent autant les mediocres, que les apparens du premier espace en sont surpassez (car de part et d'autre il y a 31′. 55″ de difference) concluent que les apparens donc du dernier espace surpassent les apparens du premier, de deux sois 31〲. 55〳, qui sait une heure, et 3〲. 50〳. Ce qui a mon advis est tont a fait hors de raison, et je ne puis concevoir de quelle saçon ils veulent comparer les jours du dernier espace avec ceux du premier qui sont beaucoup moins en nombre. La consequence aussi qu'ils en tirent est tres fausse a scavoir qu'en negligeant l'aequation du temps l'on se pouroit parfois mesconter au mouvement de la lune de plus d'un demy degre, son mouvement moyen dans le dit temps d'une heure et 3〲. 50〳, estant d'environ 34〲.

Je dis qu'ils se trompent en cela de la moitiè puis que l'aequation du temps ne va jamais qu'aux 31〲. 55〳. de sorte qu'au lieu de la lune il y peut avoir seulement faute d'environ 17〲, la quelle toutefois est assez importante pour rendre l'usage de l'equation necessaire.

Devant⁵⁾ que finir je vous diray encore que ma table que vous avez n'est pas pour servir tousjours, mais seulement pour quelque 100 ans d'icy en avant sans erreur notable, et que par consequent ce n'est pas par elle aussi que l'on peut reduire un espace du temps apparent de plusieurs siecles, au temps mediocre, comm'il est requis au compte du mouvement Lunaire quand on suppose l'Epoche fort reculee.

La cause est dans le changement de l'aphelie du soleil qui avance peu a peu dans l'Ecliptique quoyque d'un mouvement tres lent faisant environ un degrè en 60 ans. Il faut donc dans ces grands espaces de temps se servir de la régle qu'a donnè Ptolemec, qui est tres bonne et n'a point d'autre fondement que celuy du calcul de nostre Table.

5) La minute de ce qui suit se trouve sur une feuille à part.

[p. 142]

Je ne diray pas icy comment il faut l'appliquer. Vous comprenez facilement comment il faut se servir dans le calcul de la Lune, car il ne faut que reduire l'espace du temps apparent entre l'Epoche et le moment donnè au temps mediocre.