Oeuvres complètes. Tome IV. Correspondance 1662-1663
(1891)–Christiaan Huygens–
[pagina 88]
| |
No 995.
| |
[pagina 89]
| |
Now because XjGa naar voetnoot6), is to ba; as XH is to bH: that is (putting x for the number of the sides) as x to 1. therefore the power of the weight at X is to the power of the weight at b∷ x. 1. therefore the time of its descent from X to h, being let fall at X, is to the time of its descent from b to H, being let fall at b; as √1/x to 1. now because Xj is to hg; as XH is to hH∶ that is, as x to x-1. Therefore ABC representing the space Xh, and AB the proportionable time the Bullet is descending that space found as before
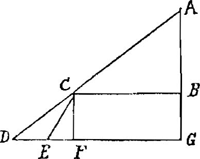 to be √1/x, let a be put for BG, the time that the said Bullet being let fall at X is passing from h to f, and let y be put for CB the velocity that the Bullet hath acquired at h in its descent from X then because AB. BC∷CF. FD. that is √1/x. y∷a. ay √x. therefore DF equals ay √x. then because Xj. hg∷DF. FEGa naar voetnoot7) (by the Petition aboue mentiond, That the encrease of the velocity is in proportion to the power of the weight; or [which is the same thing] to the perpendicular altitude of the inclination of the side.) that is x. x - 1 ∷ ay √x. x - 1/x ay√x. Therefore x - 1/x ay √x = EF. therefore Δ CEF equals x - 1/x a2y√xGa naar voetnoot8) and the Parallelogram FCBG = ay. and the Δ CBA = y/2√x. But ECBG = CBA (because hf = Xh) therefore x - 1/x ay √xGa naar voetnoot8) + ay = y/2√x, therefore  a2 y + 2 ay √x = y. therefore a2 y + 2 ay √x = y. therefore  a2 + 2 a √x = 1. therefore a2 + 2√x/x-1 a = 1/x-1. therefore a = a2 + 2 a √x = 1. therefore a2 + 2√x/x-1 a = 1/x-1. therefore a = 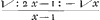 Ga naar voetnoot9) which is therefore the time that the Bullet falling from X descends the side hf. After the same manner the time the Bullet descends the third side is found to be Ga naar voetnoot9) which is therefore the time that the Bullet falling from X descends the side hf. After the same manner the time the Bullet descends the third side is found to be  , and universally the time is found to be , and universally the time is found to be 
| |
[pagina 90]
| |
l being put for the number of sides descended. now the aggregate of all these times are √∶ x2 + x/2∶ abating this series 1/s2 + s √∶ x2 + x/2 - s2 + s/2∶ s being put for 1, 2, 3, 4 &c. untill it equal x. as is euident by induction thus. if x=1. the time is √1/1 = √1. if x=2. the times are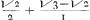 = √3 - ½√2.
if x=3. the times are = √3 - ½√2.
if x=3. the times are  =√6-½√5-⅙√3.
if x=4. the times are =√6-½√5-⅙√3.
if x=4. the times are 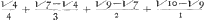 =√10-½√9-⅙√7-1/12√4.
if x=5. the times are =√10-½√9-⅙√7-1/12√4.
if x=5. the times are  =√15-½√14-⅙√12-1/12√9-1/20√5. &c.
Then because 1/s2 + s √∶ x2 + x/2 - s2 + s/2∶ are the ordinates of an Ellipsis diuided by a series of triangular numbers, therefore ABC representing that Ellipsis, =√15-½√14-⅙√12-1/12√9-1/20√5. &c.
Then because 1/s2 + s √∶ x2 + x/2 - s2 + s/2∶ are the ordinates of an Ellipsis diuided by a series of triangular numbers, therefore ABC representing that Ellipsis,
 and ACD the series of triangular numbers, and ACEB a Parallelogram upon the same base and altitude with the ellipsis; because the series of ordinates in the Parallelogram, diuided by the series of triangular numbers respectiuely equals twiceGa naar voetnoot10) AB (the series being infinit) or √∶ x2 + x/2∶ and because if from the series of ordinates in the parallelogram ACEB be subducted the series of ordinates in the Ellipsis ACB respectiuely, there remaines the series of ordinates in the Complement of the Ellipsis BCE: therefore the series of ordinates in the Complement of the Ellipsis diuided by the series of triangular numbers respectiuely is the aggregate of all the times. But this aggregate is still the same, because x is still the same, the number of sides (for which it is put) being alwayes infinit. Therefore the Bullet descends from all points of this Curve in the same time Quod &c.Ga naar einda). |
|


