Oeuvres complètes. Tome III. Correspondance 1660-1661

[p. 88]

N^o 755.
P. de Fermat à P. de Carcavy.
Appendice I au No. 754.

La copie se trouve à Leiden, coll. Huygens¹⁾
Elle a été publiée par Ch. Henry dans le Bull. di Bibliogr. T. 17.

1. Datâ quadraturâ hyperboles, datur circulus aequalis superficiei curuae paraboles circa applicatam rotatae.

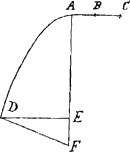
Sit data parabola AD, cuius axis AE, applicata seu semibasis DE, rectum latus ABC, quaeritur circulus aequalis superficiei curuae solidi quod ex rotatione figurae ADE, circa applicatam DE tanquam immobile circumductae consicitur. Bisecetur latus rectum AC, in B, et axi AE, ponatur in directum recta EF aequalis rectae AB, seu dimidio recti lateris, et jungatur DF, Exponatur separatim recta IQ aequalis axi AE, cuius dupla sit recta IR, fiat ut FE, siue AB, ad DF ita recta QI, ad rectam QH, et à puncto H, ducatur HG, perpendicularis ad HIR, et fiat HG, aequalis rectae DE, per



punctum I, tanquam uerticem describatur Hyperbole cuius transuersum latus sit recta IR, centrum Q et transeat hyperbole per punctum G, et sit IG. Describatur item alia hyperbole separatim cuius transuersum latus MN, sit aequale quartae parti recti paraboles lateris, hoc est quartae parti rectae AC, centrum uero sit V, rectum latus OVP, aequale transuerso lateri, sit autem hyperbole ita descripta MK, cuius uertex M, axis ML,



qui continuetur donec recta ML, sit aequalis axi paraboles AE et ducatur perpendicularis seu applicata LK, à rectangulo sub QH, in HG, deducantur duo spatia hyperbolica IGH, MKL quorum quadraturae supponuntur, et quod supererit aequetur quadrato, Diagonia istius quadrati erit radius circuli superficiei curuae, cuius dimensionem quaerimus, aequalis.

2. Esto cyclois primaria ANIF, cuius axis AD, semibasis DF, Et ab ea sormentur aliae curuae uel extra ipsam uel

1) Cette copie est de la main de P. de Carcavy.

[p. 89]

intra, quarum applicatae sint semper in eadem ratione datâ, ad applicatas primariae cycloidis.

Exempli gratia in curua exteriori AMHG, durantur applicatae GFD, HIC,



MNB, ratio autem GD, ad DF, sit data et sit semper eadem quae HC, ad CI, et MB, ad BN. In curvâ autem interiori AROE, ratio FD, ad DE, sit data, et sit semper eadem quae IC, ad CO, et NB, ad RB. Dico contingere ut curuae Exteriores qualis est AMHG, sint semper aequales aggregato lineae circularis et lineae rectae. Curuae autem Interiores, qualis est AROE, sint semper aequales parabolis primariis siue archimedeis.

Theorematis generalis enuntiationem, quando uolueris exhibebo, immo et demonstrationem.