Oeuvres complètes. Tome III. Correspondance 1660-1661
(1890)–Christiaan Huygens–No 734.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 52]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ad medium ♒. comparatis scilicet motibus apparentibus cum mediis. Deinde subjicit, duplo temporum numero differre inter se dies apparentes collatos, seu jnterualla vtriusque segmenti temporis apparentis; id est quando comparata fuerint vtraque inter se segmenta temporis apparentis, atque etiam eadem inter se temporis medii per subtractionem minoris a majori: tunc differentiam residuorum duplam esse ejus, quo in alterutro segmentorum inter se medium & apparens differunt. Quod sic se habere exemplo allato declarabimus. Sint data duo Temporis apparentis interualla, primum a meridie apparente diei 7. Nouembris 1651. ad meridiem apparentem 4. Februarii 1652. Secundum ab hoc meridie 4. Februarii ad meridiem apparentem Nouembris 6. 1652. Anno 1651 juxta Eichstadium loca ☉ vera. Nouembris 7. meridie Apparente ☉ ♒ grad. 14.′55. Ascensio Recta 222.′26. 1652. Februarii 4. meridie Apparente ☉ ♒ grad. 15.′32. Ascensio Recta 318.′1. Interuallum Dierum apparentium est 89, cui, tanquam Temporis aequalis jnteruallo, congruit motus ☉ medius grad. 87.′43.″21. Differentia Ascensionum rectarum reperitur grad. 95.′32.Ga naar voetnoot3) Deficit itaque motus medius Solis minorque est differentia Ascensionum rectarum grad. 7.′52. quare plures gradus Aequinoctialis circuli per meridianum reuolutione apparente Solis transierunt; quam si arcus Ascensionis Rectae interceptus inter loca Solis data major non fuisset motu medio Solis. Huius ideo temporis medij seu aequalis jnteruallum longius est apparente temporibusGa naar voetnoot4) 7.′52 hoc est Hor. 0.′31.″28. estque dierum 89.′31.″28. In secundo interuallo loca ☉ vera. Februarii 4. meridie Apparente ☉ ♒ grad. 15.32. Ascensio Recta 318o. 1′. Novembris 6. meridie Apparente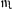 Ga naar voetnoot5) 14.40. Ascensio Recta 222. 11. Ga naar voetnoot5) 14.40. Ascensio Recta 222. 11.
Interuallum dierum apparentium est 276. motus interim aequalis Solis per hunc dierum numerum est grad. 272.′2.″ 19. Differentia Ascensionum Rectarum est partium 264.′10. Arcus igitur motus aequalis ☉ major est arcu Ascensionis Rectae inter vtrumque punctum jntercepto partium 7.′52. citius itaque reuolutione apparenti Sol est ad meridianum reuersus, quam si aequales fuissent arcus medii motus & Ascensionis Rectae longiusque numeratum est tempus apparens partium 7.′52. seu Hor. 0.′31.″28 quam medium. ab interuallo igitur dierum 276. si hocce tempus auferatur, dabitur temporis aequalis jnteruallum dierum 275. Hor. 23.′28.″32. Segmentum igitur Temporis Apparentis a medio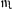 ad medium ♒ comparatum cum temporis aequalis eodem segmento, deprehenditur ab hoc deficere ′31.″28. segmentum vero a medio ♒ ad medium ad medium ♒ comparatum cum temporis aequalis eodem segmento, deprehenditur ab hoc deficere ′31.″28. segmentum vero a medio ♒ ad medium 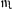 temporis apparentis cum temporis aequalis eodem segmento comparatum excedere hocce cernitur totidem ′31.″28. temporis apparentis cum temporis aequalis eodem segmento comparatum excedere hocce cernitur totidem ′31.″28.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 53]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Post comparatum penes vnum jdemque segmentum tempus apparens cum aequali, comparat etiam Ptolemaeus segmenta temporis apparentis inter se; atque etiam eadem temporis medii comparanda inter se sunt; sicque jnter se comparatis temporis apparentis segmentis, pariterque medii, collatisque deinceps jnter se segmentorum excessibus, dicit apparens ab apparenti differre duplo ejus quo apparens ab aequali in vtroque segmento differt.
Excessus igitur segmentorum Temporis apparentis differt ab excessu segmentorum temporis medii Hor. 1.′2.″56. duplo scilicet ejus, quo in vno eodemque segmento differunt ab inuicem aequalis & apparens ′31.″28. videlicet. Minores ergo seu breuiores dies apparentes differunt a majoribus seu longioribus apparentibus in datis segmentis Hor. 1.′3.″56. Minores enim apparentes aequalibus differunt ab ipsis, et ab eis deficiunt ′31.″28. Majores vero apparentes aequalibus differunt ab ipsis, eosque excedunt ′31.″28. ergo superant hi majores inaequales minores illos inaequales Hor. 1.′2.″56. tantaque etiam reperta differentia eorum est, ad differentiam segmentorum aequalium seu mediorum inter se comparata. Quod etiam sic explicari potest, Differentia duorum segmentorum inter se dierum inaequalium, major est differentiâ duorum segmentorum dierum aequalium seu mediorum, & dupla ejus qua apparentes a medijs in vno eodemque segmento differunt. Theon Alexandrinus haec leuiter attigit in CommentarijsGa naar voetnoot6) in μαθηματιϰὴυ σύνταξιν; Iohannes RegiomoutanusGa naar voetnoot7) paulo clarius explicuitGa naar voetnoot8). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 54]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cum igitur in Lunae motibus aequalibus colligendis duo temporis apparentis jnterualla posita erunt & inter se comparabuntur, atque etiam motus aequales, vt sciamus quanta magnitudine motus vnius jnterualli superet motum alterius, error in illis motibus mediis computandis dierum omissa aequatione ad ′35 fere excrescere potest, vt recte est a Ptolemaeo adnotatum. cujus Methodus in aequandis temporum jnteruallis recte procedit; in reducendis vero temporum punctis ab apparenti ad aequale a verò longe aberrat, cum Epochae Temporis apparentis addat jnteruallum temporis aequalis.
Exemplum erroris qui in motu ☾ admitteretur omissa aequatione dierum.
Volo inquirere quantum superet motus ☾ medius secundi jnterualli motum medium primi datis temporibus apparentibus.
Motus ergo ☾ aequalis accurate computatus esset, si dies apparentes aequales essent: at cum reductione opus habeant, vt aequalis ☾ motus exactè numeretur, adhibenda sunt jnterualla temporis medii, & per ea Lunae motus est colligendus.
Motus igitur ☾ per differentiam jnteruallorum temporis apparentis major est ′34.″33. motu ipsius computato per jnterruallorum temporis medii differentiam. Motus vero in vno eodemque jnteruallo computatus per tempus apparens et aequale differt solummodo ′17.″16. vt ex comparatione motuum primi vel secundi interualli inter se constat. In his omnibus numeros Tabularum nostrarum Philolaïcarum vsurpauimus.
Exemplum, quo arguitur falsa Methodus Ptolemaïca in reducendo puncto dato Temporis apparentis ad Temporis aequalis respondens punctum. Sit datus Meridies apparens 4. Februarij 1652 epocha posita in meridie appa- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 55]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rente Diei 7. Nouembris 1651. in qua Tempus Medium et Apparens concurrunt ex hypothesi. Ex superiori calculo constat jnteruallum dierum aequalium longius esse debuisse quàm apparentium ′31.″28. Quare cum fuit Meridies apparens Februarij 4., Tempore Aequali debuit esse Februarii 4. Hor. 0.′31.″28. Supponatur deinde Meridies apparens 4. Februarij 1652 pro epocha, in qua concurrant etiam Tempus Apparens & aequale, & retro computetur Tempus ad Meridiem apparentem diei 7. Nouembris 1651. eadem aequatio temporis inuenietur addenda jnteruallo Temporis Apparentis, vt aequalis temporis jnteruallum habcatur Dierum 89. Hor. 0.′31.″28. quo ablato a 4. Februarij meridie apparente, jncidemus in Nouembris Diem 6. Hor. 23.′28.″32. quare reuera & ϰατὰ ϕύσιν punctum temporis aequalis Meridiesque non concurrebat cum meridie apparente Die 7. Nouembris quando epocha ibi constituta est. Tale porro absurdum sequitur. cum respectu epochae quarto Februarij alligatae, tempus apparens retro computatum fuerit ad meridiem 7. Nouembris & reperiatur aequatio Temporis addito jnteruallo dierum 89 apparentium vt aequales dies habeantur 89. Hor. 0.′31.″28. jncidemus in Diem 6. Nouembris Hor. 23.′28.″32. Tempore Aequali. Cumque rursus positâ epochâ Nouembris 7. meridiei apparentis tempus deinceps computatur ad meridiem apparentem 4. Februarij aequatio pariter addito jnteruallo dierum apparentium ′31.″28 vt interuallum dierum aequalium habeatur 89. Hor. 0.′31.″28 & Meridiem apparentem 4. Februarij jncidemus tempore aequali in Februarij Diem 4. Hor. 0.′31.″28. Habemus proinde respectu duorum punctorum Temporis apparentis duo puncta Temporis Medii per Aequationem jnuenta; subtrahatur antecedens a sequenti, colligemus spatium temporis aequalis Dierum 89. Hor. 1.′2.″56. quod est falsum; nam ex veris causis jnteruallum datum dierum solummodo 89. Hor. 0.′31.″28 est. Hoc si vidisset Ptolemaeus, maxime differre ab aequali apparens circa medietatem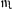 & ♒ conclusisset; deprehendissetque perperam conjungi in illis locis, vt et in jnitio Piscium & Epocha Nabonassari, medium Tempus cum apparente. animaduertisset etiam quod Meridies Temporis aequalis Meridiem apparentis sequitur, Sole & ♒ conclusisset; deprehendissetque perperam conjungi in illis locis, vt et in jnitio Piscium & Epocha Nabonassari, medium Tempus cum apparente. animaduertisset etiam quod Meridies Temporis aequalis Meridiem apparentis sequitur, Sole 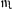 medium tenente; contra vero quod Meridies temporis aequalis antecedat Meridiem apparentem, Sole medietatem ♒ tenente; tandemque notauisset ex sua hypothesi, duplo fere majorem aequationem Temporis sequi, quam reuera & secundum naturam sit. medium tenente; contra vero quod Meridies temporis aequalis antecedat Meridiem apparentem, Sole medietatem ♒ tenente; tandemque notauisset ex sua hypothesi, duplo fere majorem aequationem Temporis sequi, quam reuera & secundum naturam sit.
Ismael Bullialdus. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||

