No 718.
Christiaan Huygens à [Ism. Boulliau.]
12 février 1660.
La lettre se trouve à Leiden, coll. Huygens.
Elle est la réponse aux Nos. 712 et 716. Ism. Boulliau y répondit par le No. 723.
le 12 Febr. 1660.
Monsieur
J'ay encore a vous remercier du dessein
Ga naar voetnoot1) de l'horologe de Monsieur le Grand duc, lequel comme aussi le premier
Ga naar voetnoot2) je ne scay si vous voulez que je vous renvoye, ou si vous en avez gardè des copies. Cettuila du Palais de Medicis estant construit depuis la publication du mien je m'estonne que l'on n'a pas voulu l'imiter, puis que le changement que l'on y a apportè produira necessairement un mauuais effect. La pesanteur du pendule estant appuyée sur l'axe de son mouuement, il faudra la moitiè d'avantage de poids pour faire aller l'horologe, qu'il n'y a à ceux de ma façon, ou le pendule est suspendu à part. Pour y remedier je voy qu'ils ont pris le pendule extremement leger, mais il se ressentira d'avantage des fautes de l'horologe, tellement que la justesse qui est la seule chose que l'on y cherche ne sera pas telle qu'avec nos pendules pesants, mesme sans ma derniere addition. Je vous assure Monsieur que je m'appercois desia clairement de l'inegalitè des jours, et je croy mesme qu'à l'avenir je la pourray mesurer, et demonstrer par experience qu'il faut joindre les deux causes entieres, des quelles vous rejettez la moitiè de l'une. Je voy que vostre seconde table page 8
Ga naar voetnoot3) est faite des demies prostaphaereses du soleil converties en temps, et que si vous aviez pris les entieres, vostre table universelle de la page suivante auroit estè la mesme que celle de Mullerus page 280
Ga naar voetnoot4); au moins en mesmes intervalles de
temps elle auroit donnè mesme aequation. Sed de his alias latius, car je suis encore a esplucher cette matiere; cependant je vous prie d'une chose, c'est de me dire ce que Ptolemee et Copernicus apres luy ont voulu signifier quand ils escrivent que dies apparentes longiores excedunt breviores duplo ejus quo ijdem apparentes superant vel deficiunt a medijs: Vous l'expliquez ad literam P
Ga naar voetnoot5), quod apparentes collecti à medietate ♒ ad principium
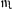
excedunt collectos à principio
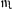
ad medietatem ♒ horâ 1.6′ 40″. comment comparez vous les jours qui sont à principio
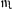
ad medium ♒, a ces autres qui sont presque trois fois autant en nombre? Je ne croy pas aussi que pour avoir le vray lieu


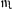 excedunt collectos à principio
excedunt collectos à principio