Oeuvres complètes. Tome II. Correspondance 1657-1659

N^o 678.
Christiaan Huygens à Gregorius a St. Vincentio.
1659.
Appendice au N^o. 677.

La pièce se trouve à Leiden, coll. Huygens.

Sphaeroidis omnis oblongi superficies aequalis est circulo cujus circuli semidiameter est media proportionalis inter semidiametrum sphaeroidis et lineam aequa-

[p. 501]

lem utrisque his, diametro Sphaeroidis et arcui peripheriae descriptae super axe sphaeroidis cujus peripheriae diameter sit ad dictum axem ut axis ad distantiam umbilicorum in sectione per axem.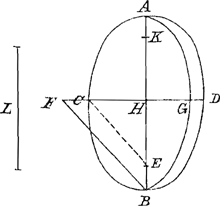

Sit sphaeroides oblongum cujus axis AB, sectio per axem ellipsis ACBD, in qua minor axis atque idem diameter sphaeroidis sit CD, centrum H. umbilici E, K. Et jungatur EC, eique parallela agatur BF, quae occurrat productae DC in F. dein centro F radio FB describatur super axe AB arcus BGA. Et sit inter semidiametrum HC et rectam aequalem utrisque simul diametro CD et arcui AGB, media proportionalis L recta. dico circulum hoc radio descriptum aequalem esse superficiei sphaeroidis ACBD.

Sphaeroidis omnis lati superficies aequalis est circulo cujus semidiameter media est proportionalis inter diametrum sphaeroidis et rectam aequalem lineae parabolicae cujus basis sit axis sphaeroidis, altitudo vero aequalis quartae parti distantiae umbilicorum in sectione per axem.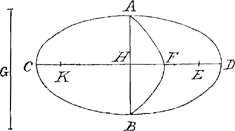

Esto latum sphaeroides cujus axis AB, sectio per axem ellipsis ACBD, in qua major axis qui hîc diameter sphaeroidis vocatur sit CD, centrum H, umbilici, E, K. Sit autem descripta super AB parabola AFB cujus vertex F bifariam dividat HE. Esto autem inter rectam CD et curvae parabolicae AFB longitudinem media proportionalis G. Dico si radio G circulus describatur aequalem fore superficiei sphaeroidis propositi.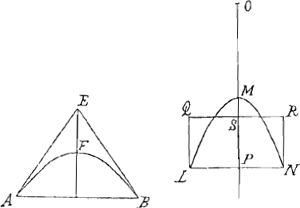

Inveni autem quomodo recta curvae parabolicae aequalis sumi possit posita hyperbolae quadratura, hoc modo. Esto data parabolae portio recta AFB. Et in eadem basi triangulum isosceles constituatur AEB altitudinem portionis duplam habens. deinde sit hyperbolae portio LMN, cujus semilatus transversum MO aequale sit basi portionis parabolae AB. tota vero OMP quae inter centrum sectionis et basin LN intercipitur,

[p. 502]

sit aequalis duabus AE, EB. Jam si ponatur parallelogrammum LQRN aequale esse portioni hyperbolicae LMN, dico rectam SO quam abscindit QR, aequalem esse curvae parabolicae AFB.

Si in eadem basi consistant conoides parabolicum et conus rectus, sit autem coni altitudo dupla ad altitudinem conoidis, erit superficies coni ad superficiem conoidis, utrâque sine basi sumtâ, ut latus coni triplum ad idem latus duplum junctum ei lineae quae sit ad diametrum baseos sicut eadem diameter ad totum ambitum trianguli per axem.

Ut si sit conoides parabolicum ABC et in eadem basi conus ADC cujus dupla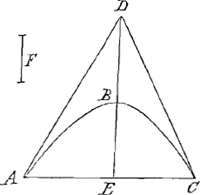



sit altitudo ejus quae conoidis, sicut autem ambitus trianguli ADC per axem ad basin AC ita sit haec ipsa ad lineam quandam F. Dico superficiem coni ad superficiem conoidis, utrâque sine basi sumptâ, esse ut triplum latus AD vel DC, ad idem latus duplum additum lineae F.

Unde facile colligitur, si fuerit AD aequalis AC, superficiem conoidis curvam ad circulum baseos suae fore ut 14 ad 9.

Si vero AD sesquialtera AC, dictam superficierum rationem fore ut 13 ad 6.

Et si fuerit AD dupla AC, ut 14 ad 5. Semperque commensurabiles fore, si AD sit commensurabilis AC.

Itaque vides Parabolici Conoidis superficiem absolutè me invenisse quemadmodum Sphaericam Archimedes. Sphaeroidis autem oblongi ita, ut inventa ponatur circuli quadratura. Item lati sphaeroidis ut quadratura hyperbolae ponatur. Ex qua eadem etiam hyperbolici Conoidis superficies invenitur.

At quoniam constructio non aeque concinna est hîc eam non adjunxi. Possumus autem semper cum datum est conoides hyperbolicum invenire sphaeroides latum, vel contra, et utriusque simul superficiei circulum absolute aequalem constituere.