Oeuvres complètes. Tome II. Correspondance 1657-1659
(1889)–Christiaan Huygens–No 473.
| |
[pagina 151]
| |
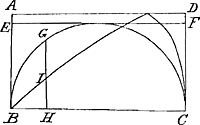 vt clarius euadat, esto BIC curua circa axem BC, cuius proprietas his terminis exprimitur ay3 - y4 ∞ x4. Et super eadem BC diametro, semicirculus BGC. Aio, si cadat ex quolibet puncto semicirculj normalis GIH, secans curuam in I, tres BH, HI, HG, esse in continuâ ἀναλογίᾳ. Quod breuiter ostendo. BH est y, HI ex proprietate lineae est 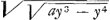 , GH vero ex proprietate circulj etGa naar voetnoot1) , GH vero ex proprietate circulj etGa naar voetnoot1) 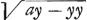 , Patet itaque tres, y, , Patet itaque tres, y, 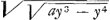 , , 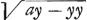 esse proportionales, cum productum extremorum aequale sit quadrato medij. Hoc posito, sequitur euidenter, si semicirculus BGC circa tangentem BA reuoluj intelligatur, jtemque curua BIC circa rectam BC, solidum ex hac genitum fore semispirae subduplum; Cum rectangulum BHG (quod in reuolutione duplicator) sit semper aequale quadrato HI. Hoc enim a pluribus hactenus ostensum est, nec Te latere arbitror. Itaque vides sj nota sit mensura solidj ex curuâ BIC siue eiusdem ratio ad cylindrum ortum ex reuolutione parallelogrammj BD, notam pariter fore rationem semispirae (vtpote duplae) ad eundem cylindrum, et per consequens ad cylindrum sibj circumscriptum, cum ratio cylindrorum tam semispirae quam solido nouo circumscriptorum nota sit. Si vero pateat ratio semispirae ad suum cylindrum, notam quoque esse rationem circulj ad quadratum circumscriptum non diffiteris; in quo vim
ἀπαγωγῆς nostrae consistere ad Te scripsj. Vlterius autem aliam explicare quae his terminis continetur ay3 - y4 ∞ aaxx superuacaneum arbitror, cum et a Te factum sit, et per se innotescat. Itaque ad Cissoidem venio. Sit illa vel potius eius esse proportionales, cum productum extremorum aequale sit quadrato medij. Hoc posito, sequitur euidenter, si semicirculus BGC circa tangentem BA reuoluj intelligatur, jtemque curua BIC circa rectam BC, solidum ex hac genitum fore semispirae subduplum; Cum rectangulum BHG (quod in reuolutione duplicator) sit semper aequale quadrato HI. Hoc enim a pluribus hactenus ostensum est, nec Te latere arbitror. Itaque vides sj nota sit mensura solidj ex curuâ BIC siue eiusdem ratio ad cylindrum ortum ex reuolutione parallelogrammj BD, notam pariter fore rationem semispirae (vtpote duplae) ad eundem cylindrum, et per consequens ad cylindrum sibj circumscriptum, cum ratio cylindrorum tam semispirae quam solido nouo circumscriptorum nota sit. Si vero pateat ratio semispirae ad suum cylindrum, notam quoque esse rationem circulj ad quadratum circumscriptum non diffiteris; in quo vim
ἀπαγωγῆς nostrae consistere ad Te scripsj. Vlterius autem aliam explicare quae his terminis continetur ay3 - y4 ∞ aaxx superuacaneum arbitror, cum et a Te factum sit, et per se innotescat. Itaque ad Cissoidem venio. Sit illa vel potius eius
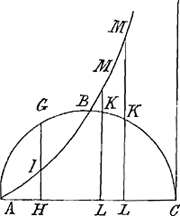 quadrans AB, descriptus in quadrante circuli AB. Constat sumpto quolibet puncto G & ductâ normali GHI quatuor CH, HG, HA, HI esse in continuâ ἀναλογίᾳ. Nunc erigatur in C normalis infinita, sumptoque vltra B quolibet in semicirculo puncto K, cadat normalis KL, quae producj versus K intelligatur ad M, ita vt tres KL, LA, LM, sint proportionales, erunt consequenter quatuor in continuâ ἀναλογίᾳ CL, LK, LA, LM. Hoc vero semper fiat donec per puncta M ducj possit curua, vt solet. Eam nunquam concurrere cum normalj in C erectâ, si ostendere vellem, operam perderem, cum vel ex ipsâ descriptione euidens sit. Accedit τεϰμήριον ex tangentibus quas olim duxj, et a Te factum, vel fierj nullo negotio posse non dubito. Nunc igitur superiorem demonstrandj methodum applica, et claré perspicies semispi- | |
[pagina 152]
| |
ram, solido acuto infinito quod ex Cissoidis circa asymptoton reuolutione oritur, esse aequalem. Ex quo tertiae ἀπαγωγῆς ratio innotescit, et, quod antiquos latuisse arbitror, ex Cissoidis contemplatione non duarum mediarum inter datas duntaxat ἀνάλυσιν deduci posse, sed ipsius etiam circulj mensuram. Vides nunc, vt opinor, me nihil in Geometriae leges peccasse, nec ψευδαρίου sed ἀσαϕείας nomine incusandum, quam ea, qua soles, comitate excusabis. Quod si forsitan aliquid Tibj hactenus non satis enucleatum esse videatur, scribe sodes et a me solutionem expecta. In hoc enim campo satis versatum esse me meminj, vberemque nouorum solidorum atque ἀπαγωγῶν messem collegisse. Haec tecum (vt et alia cum iubebis) sub eâ secreti fide comunia esse voluj, quam in Tuis seruaturum me promisi et porro praestabo. Versiculos meos Viro Maximo Parenti tuo Tibique probarj supra spem accidit imo supra votum. Hoc animos adiecit vt ad Te mitterem ἐπιγραμμάτιον in quo ad diem qua fluuius alueum supergressus est, qua detumuit, ac ad preces quae publicé institutae sunt, allusj. Inuenies autem in eius versibus aeram huius anni quater expressam. VnDas MathIas In pLateas CongerIt,
CeDIt, geMItqVe LegIa;
LaMbertVs orat, et preCantIs In fIDe
abeVnt CaLenDIs MartIIs.
Vale Vir Praestantissime et vt facis amare porro perge
Tui obseruantissimum Renatum Franciscum Slusium.
14 Martij 1658.
Nobilissimo Clarissimoque Domino Domino Christiano Hugenio de Zulichem &c. A la Haye. VI |
|

