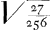Oeuvres complètes. Tome II. Correspondance 1657-1659
(1889)–Christiaan Huygens–No 472.
| |
[pagina 149]
| |
cum epistola tua mihi traderetur itaque et ille plurimum tunc dexteritatem in his tuam collaudavit. In reliqua vero epistola cum pseudarij factam mentionem videret, idque quo pertineret ex me audisset; Vide sis inquit, Aristarche etiam atque etiam, necubi tute in errorem incideris. Hinc diligentius denuo coepi expendere quae superioribus literis circa quadraturam ἐξ ἀπαγωγῆς attuleras, sed prorsus ita ut dixi sese rem habere comperi. Quod, ne pluribus te morer, sequenti demonstratione
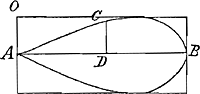 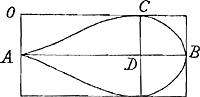 perspicuum reddam. Binae quas exposuisti curvae sunt ACB, EFGGa naar voetnoot1). quarum prioris haec est proprietas ut positâ AB diametro ∞ a. AD ∞ y, et DC applicatâ ∞ x, fiat ay3 - y4 ∞ x4. Posterioris verò, ut ijsdem positis sit ay3 - y4 ∞ aaxx. Hoc igitur constat solidum ex conversione curvae prioris circa axem AB esse ad cylindrum à rectangulo circumscripto eâdem conversione factum sicut area posterioris curvae ad circumscriptum sibi rectangulum, quare cum affirmes dictum solidum ad dictum cylindrum eandem rationem habere, quam habet circulus ad circumscriptum quadratum etiam area curvae posterioris ad circumscriptum rectangulum rationem eam habebit quae est circuli ad circumscriptum quadratum. et haec nimirum est ἀπαγωγὴ tua. Quae corruet si ostendero multo minorem esse rationem dictae areae ad □ circumscriptum. Ostendam autem hoc modo. Sumpta AD ∞ ¾ AB, fit 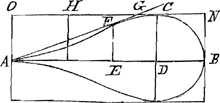 DC maxima applicatarum atque adeo altitudo rectanguli BO estque DC ∞ 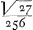 Ga naar voetnoot2), si pro AB statuatur unitas. Ga naar voetnoot2), si pro AB statuatur unitas.
Porrò sumpta AE ∞ ½ AB fit applicata EF ∞ ¼ AB sive subdupla AE: Et si per. F ducatur recta AFG ea tangit curvam in F. Quae quidem omnia vel perspecta tibi sunt vel nullo negotio vera esse deprehendes. Est itaque nunc trapezium AGNB majus area curvae ACBA. Sed trapezium AGNB ad ▭ BO minorem dico habere rationem quam circulus ad circumscriptum quadratum. Ergo multo minorem habebit area curvae ACB ad ▭ BO. Illud sic fiet manifestum. Quoniam AE est dupla EF, erit quoque GO dupla OA. unde quadratum AH aequale ∆lo AGO. ideoque ▭ re- | |
[pagina 150]
| |
liquum HB ∞ trapezio AGNB. Oportet igitur ostendere rationem ▭i HB ad ▭ BO, hoc est lineae HN ad ON minorem esse quam circuli ad circumscriptum quadratum. Dixi DC sive AO hoc est OH esse ad AB hoc est ON ut 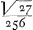 ad 1. Ergo OH ad ON majorem habet rationem quam 5/16 ad 1, hoc est quam 5 ad 16. ac proinde HN ad NO minorem quam 11 ad 16. Atqui circulus ad circumscriptum quadratum majorem habet quam 11 ad 15, ac ferè eam quam 11 ad 14. Ergo &c. Illud quidem quod de spirae ad cylindrum suum ratione adduxisti verum est, sed aequationum comparatione quali usus fueris adhuc ignoro, quod si explicasses, fortasse causam erroris detexissem, nunc eam tibimet quaerendam relinquo. ubi vero inveneris indica quaeso num alteram quoque ἀπαγογὴν quam ex cissoidis solido excogitasti eadem labe vitietur. Utriusque jacturam ut minus graviter feras alia tecum postea communicata efficiam. quam occasione hujus ἐλέγξεως adinveni. Vale Slusi Praestantissime et me ama ad 1. Ergo OH ad ON majorem habet rationem quam 5/16 ad 1, hoc est quam 5 ad 16. ac proinde HN ad NO minorem quam 11 ad 16. Atqui circulus ad circumscriptum quadratum majorem habet quam 11 ad 15, ac ferè eam quam 11 ad 14. Ergo &c. Illud quidem quod de spirae ad cylindrum suum ratione adduxisti verum est, sed aequationum comparatione quali usus fueris adhuc ignoro, quod si explicasses, fortasse causam erroris detexissem, nunc eam tibimet quaerendam relinquo. ubi vero inveneris indica quaeso num alteram quoque ἀπαγογὴν quam ex cissoidis solido excogitasti eadem labe vitietur. Utriusque jacturam ut minus graviter feras alia tecum postea communicata efficiam. quam occasione hujus ἐλέγξεως adinveni. Vale Slusi Praestantissime et me ama
Tui |
|