Oeuvres complètes. Tome I. Correspondance 1638-1656

N^o 172.
G.A. Kinner a Löwenthurn à Christiaan Huygens.
3 janvier 1654.

La lettre se trouve à Leiden, cóll. Huygens.
Elle est la réponse au No. 171. Chr. Huygens y répondit par le No. 176.

Illustris ac Generosissime Domine, Domine ac Patrone colendissime.

Salutem â Domino et felicissimum ineuntis Novi anni auspicium praevijs obsequijs meis Dominationi Tuae animitus apprecor.

Non iniuriâ, ut video, è literarum tuarum diuturna emansione mearum amissionem ominabar; quas equidem immeritò luges, Nobilissime Hugeni; fortassis enim

[p. 262]

vel ideo sinistram illam fortunae subiere vicem, quia conspectu tuo erant indignae. Jnserueram illis Theorema opticum refractionem concernens, multum ante aliquot annos apud nos disputatum occasione thesium quarundam de Jride, quas professor Matheseos Pater Balthassar Conradus proposuerat. Quandoquidem ergo de refractione, quae genesin Jridis ingreditur, quaerebatur, venit in quaestionem, an etiam radij qui tangunt globulos pluvios in quibus effigiatur Jris refringantur perinde ac ceteri secantes eosdem. Jpse negantibus ceteris tangentium refractionem demonstrabat hoc discursu, quem tuo iudicio volo subiectum. Sit punctum aliquod Solis A,



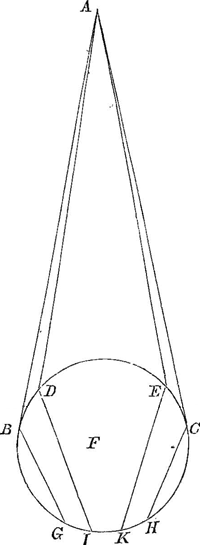â quo in sphaerulam BCDE incidant radij AB, AC tangentes eandem in punctis B, C; AD et AE verò secantes. Dico tangentes AB, AC etiam refringi. Cum enim propter medium guttae densius quam sit aer fiat refractio radiorum ad perpendicularem, inclinabuntur omnes refracti radij versus centrum F, claudenturque terminis cadentibus intra sphaeram, verbi gratia terminis BG, CH. Dico terminos radiorum refractorum BG, CH oriri â tangentibus. Sint enim radij AD, AE secantes sphaeram, sintque DI, EK ab illis refracti, dico hos non terminare omnes refractos, quia cùm arcus BD, EC, qui tangentem inter et secantem interiacent, in sententia Mathematicorum sint adhuc in infinitum divisibiles, poterunt inter B et D, itemque inter E et C cadere alij radij secantes, qui in sphaeram refringantur, adeoque secantes AD, AE refracti in DI, et EK non terminant spacium radiorum refractorum. Atque idem discursus valet pro omnibus alijs sphaeram secantibus. Cum ergo constet esse aliquem terminum radiorum intra sphaeram refractorum, et ille non oriatur â secantibus, necesse est oriri â tangentibus^a). Radij ergo tangentes globulorum refringuntur. Hic tenor erat theorematis tibi transmissi, quem hic repeto et super eo sensum tuum expeto, mecum postea aperturus. Maiorem in modum me delectas, quòd ais tractatum tuum opticum ad finem esse deductum; sed contristas quod in annum adhuc premi velis. Vt quid enim tam nobili partui lucem et amicis gaudium tibique congratulationem invideas? Sed in illo precor, nè omittas idoneam aliquam rationem elicere è Theorematibus tuis, cuius auxilio admiranda illa colorum genesis iridem comitari solita explicetur. Nam illa abstrusior, nisi fallor, est, quàm ut illam Cartesius imaginario suo, nescio quo particularum lucidarum gyro attigerit; illud enim meo iudicio (pace tanti viri



tuâque dixerim) magis est confingere, quam philosophari. Jn quo et illud tu ipse in aliò genere meritò carpis, quòd in casu, quo globulus A aequalis globulo B quatuor partibus celeritatis impellitur in globu-

a) Ego demonstravi quod terminus non fit a tangente radio, sed ab alio [Chr. Huygens].²⁾

2) Voyez la Lettre No. 176.

[p. 263]

lum B, velit ipsi B partem celeritatis communicare, et cum tribus reliquis resilire. Jllud enim unâ tecum contra rationem puto, et experientiae manifestae refragari. Vnde enim globulo A vis ad resiliendum? cum eadem vis, quae movet globulum A, adaequata etiam sit globulo B utpote ipsi A aequali, adeòque ipsum potius propellet, quàm ab eodem repellatur. Globulus ergo B accipiens impetum ab A feretur in oppositum, ipsum verò A coget quiescere, ut pote cuius impetum obstando repressit. Eadem mens est Domino Doctori Marci, qui et illud in libro suo de proportione motûs addit, si in duos globulos aequales A, B, sibi contiguos directò impingat tertius C, etiam bellici tormenti violentiâ excussus, A quidem movendum in partem oppositam,



B verò omnis motûs fore expertem: quod prorsus admirandum est, ut impetum machinae bellicae sustineat tantillus globus^b), cuius alias violentiae cedunt omnia. Apud eundem quoque invenies, si quotcunque globulos aequales iuxta se positos feriat alius aequalis, omnes praeter remotiorem fore immotos; sicut et illud quod futurum sit, si maior feriat minorem, aut ab eodem feriatur, et plura alia scitu non incuriosa; in quo tamen obscuritatem in demonstrando plerique arguunt, quorum iudicio non invitus accedo. Jn Jride sua multum â Cartesio discrepat; at illius explicatio mihi nequaquam satisfacit, quam ut verum fatear, necdum satis penetro. Nihilominus virum ingeniosissimum maximi facio, et obscuritatem potius virtuti imputo; habent enim hoc ingenio praecellentes, ut omnium aliorum ingenia secundum proprium velint mensurari; pateatque etiam alijs fore clara omnia, de quibus illi non ambigunt. Miseras ad me in penultimis tuis constructionem tuam quâ solvis problema de sectione sphaerae in data ratione, cuius, quia mihi vehementer placet constructio, si demonstrationem non invideris, rem utique mihi feceris quàm gratissimam. Absolvi tandem impressionem opusculi mei pro quadratura circuli Reverendi Patris Gregorij â Sancto Vincentio¹⁾ ad quem sequenti hebdomada duo exemplaria transmittam, è quibus unum ut spero per eundem ad te perveniet. His Vale Felicissime Hugeni et laboribus tuis Mathematicis orbem illustra, viveque memor illius, qui est

Perillustris ac Generosissimae Dominationis Tuae Servus paratissimus Godefridus Aloysius Kinner de Löwenthurn.

Dabam Pragae 3 Januarij 1654.

Perillustri Generosissimoque Domino Christiano Hugenio etc. Domino ac Patrono mihi Colendissimo observandissimoque.

6.

Hagae Comitis.

s' Graven Haage.

b) Atque C non maior debet esse quam B vel A [Chr. Huygens].

1) Voyez la Lettre N^o. 167, Note 3.

2) Voyez la Lettre No. 176.