Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 254]

N^o 168.
Christiaan Huygens à Fr. van Schooten.
10 décembre 1653.

La lettre, la minute et la copie se trouvent à Leiden, coll. Huygens.
Fr. van Schooten y répondit par le No. 169.

Christ. Hugenius Clarissimo Viro Domino Francisco Schotenio S.

Mitto ecce quam petijsti alteram Problematis Apolloniani de Rhombo constructionem, in qua demonstratio brevior est quam in priori, Et una ad utrumque casum accommodata. Item qua ratione Methodum tuam inveniendi gravitatis centra promoverim ita ut ad Quadraturam etiam deducat Parabolae et similium spatiorum. Esto itaque hujus in parabola exemplum; quae sit ABC, axis BD, et rectangulum parabolam continens AEFC, lateribus AE, CF axi parallelis.

Postquam igitur methodo tua inventum erit gravitatis centrum parabolae punctum H ut BH sit^a) 3/5 BD: ad eundem modum inveniendum quoque centrum gravitatis I spatij ABG, quod^b) binis constat residuis quale AEB. Hoc autem fieri potest, quoniam ejus quoque naturae est spatium ABG, ut pars ejus quaevis quae abscinditur rectâ lineâ basi AG parallelâ, qualis est verbi gratia ΩBX, ad totum GBA notam habeat proportionem; eandem nempe quam ▭ XI, IB ad ▭ AE, EB, hoc est quam cubus IB ad cubum EB. Et hanc quoque habet proprietatem spatium GBA, ut à centro gravitatis axis EB eadem proportione secetur, atque axis partis cujusvis abscissae ΩBX à centro gravitatis suo, quae facile ostendi possent. Invenietur igitur BI esse^c) ¾ BE ut I sit centrum gravitatis GBA. Erit autem centrum gravitatis partis EBA in linea IX; Item centrum gravitatis semiparabolae ABD in hΔ ipsi DA parallela, quia videlicet H est centrum gravitatis totius parabolae. Verum ad indagandam quadraturam opus est ut sciamus in quo lineae HΔ puncto dictum gravitatis centrum consistat. Ponatur in O, et ducta PQ basi AD parallela abscindat particulam APQD; cujus centrum gravitatis ponatur esse T punctum: et jungatur TO, quae producta occurrat AD in R. Pro-

a) Dans la minute: sesquialtera HD.

b) Dans la minute: a linea BE bifariam et in partes similes secatur.

c) Dans la minute: tripla reliquae IE.

[p. 255]

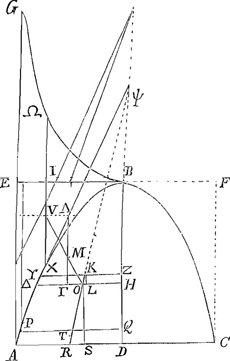
ducta vero versus O transibit necessario per centrum gravitatis partis reliquae PBQ, quod sit K. Et ducatur YKZ parallela^d) AD. Fingendum est autem sicut in tua methodo, quod OT aequalis OR, quasi T incidat in R, quoniam scilicet minimam imaginamur particulam^e) AQ. Ideo autem et centrum gravitatis in medio ipsius situm intelligere licet, quia haud aliter quam exiguum rectangulum consideratur, quantum ad haec. Ergo T sive R bifariam secare debet AD. Sit jam BD ∞ a item latus rectum ∞ a, ergo et DA erit a. Porro HO sit x et DQ, y. Sint autem LS et KL axi BD parallelae. Ergo Calculus erit hujusmodi.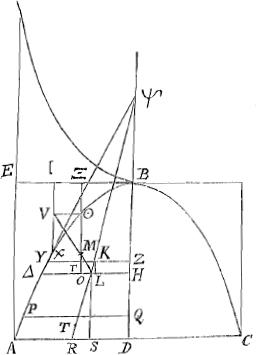

^f)

Postquam igitur inventum est quod HO ∞ ⅜ AD, et quod EI ∞ 2/8 EB; sit jam rectanguli ED centrum gravitatis M, et ducatur OM, quae producta occurrat IX in V. Igitur V centrum gravitatis est residui AEB. Sit item ΓΜΞ parallela DB,

d) Dans la minute: ΔH.

e) Dans la minute: APQD.

f) Dans la minute: - 3/2 a + 3x ∞ - x.
4 x ∞ 3/2 a.
x ∞ ⅜ a.

[p. 256]

quae quidem dividet EB bifariam. Ergo quoniam EI est 2/8 EB erit et ΙΞ 2/8 EB. Et quoniam OH est ⅜ EB, erit ΟΓ ⅛ EB. Ergo ΙΞ dupla est ipsius ΓΟ. quare et VM dupla MO: ac proinde per 7 libri 2 Archimedis de Aequiponderantibus etiam semiparabola ABD dupla residui AEB. Ideoque subsesquialtera rectanguli ED. ex quo quadratura manifesta est. Vides autem haec ad similis naturae plana applicari posse. qualia sunt Parabolae istae altioris gradus quas nosti.

Hisce expeditis constructionem nunc scribam Apolloniani problematis quae sic habet. Sit datus rhombus ADBC cujus productum latus DB, Et data sit linea G. Oporteatque ducere rectam ANF, ut pars intercepta NF sit datae G aequalis. Ducatur diameter AB, et quadratis ex G et AB sit aequale quadratum AH, et ducatur HE ipsi BA parallela. atque ad eam ex A ponatur AE aequalis G, et sit, recta FAN dico NF datae lineae G aequalem fore. Etenim in producta BD, ponatur ipsi aequalis DR. et sit RK parallela DA vel BC, eique occurrant FA, BA, HE, in punctis M, Q et K. Et jungatur RA et producatur ad P.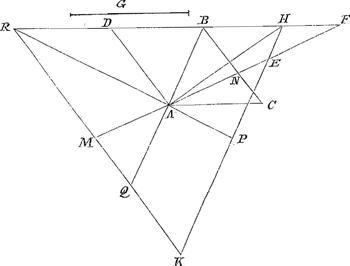

Quoniam igitur DR aequalis est DB, et RM parallela ipsis DA, BN, erit et MA aequalis AN, et QA aequalis AB. angulus autem BAR rectus est quum sit in semicirculo; (nam DB, DA, DR inter se aequales,) Quare et anguli ad P recti erunt, nam BAQ, HEK inter se parallelae; et erit HP aequalis PK.

Est igitur quadratum AH aequale quadrato AE una cum rectangulo HEK. Sed idem quadratum AH ex constructione aequale est quadratis ex G seu AE et ex AB. Ergo quadratum AB aequale rectangulo KEH. Quamobrem erit KE ad AB ut AB ad EH. Verum KE ad AB seu QA, ita est EM ad MA: et ut AB ad EH ita est AF ad FE, utrumque propter similes triangulos. Igitur EM ad MA ut AF ad FE: ideoque EA ad AM ut AE ad EF. Aequalis itaque EF ipsi AM hoc est ipsi AN. Quare et FN ipsi AE hoc est datae G. Quod erat demonstrandum.

Esto rursus ACBD rhombus cujus producta sint latera BC, BD. Oporteatque ducere rectam NF per angulum A transeuntem quae sit aequalis datae G.

[p. 257]

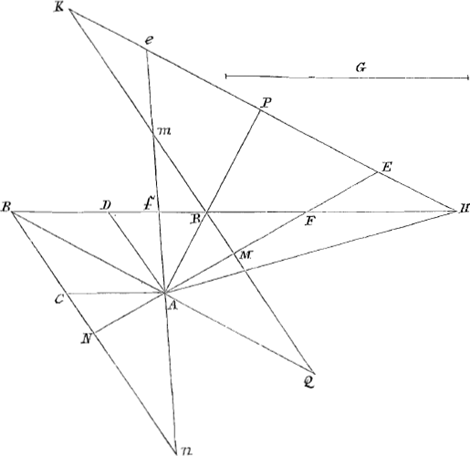Erit in schemate adjecto sicuti propositum est, eadem constructio et demonstratio quae in casu superiore.

Hagae. 10 Dec. 1653.