Oeuvres complètes. Tome I. Correspondance 1638-1656

[p. 224]

N^o 153.
Christiaan Huygens à G. van Gutschoven.
6 mars 1653.

La minute et la copie se trouvent à Leiden, coll. Huygens.
La lettre est la réponse aux Nos. 151 et 152.

do. 6 Martis 1653.

Clarissimo Eruditissimoque Viro Domino Gerardo Gutschovio Chr. Hugenius S.D.

Literae tuae quas 10 Februarii dederas non ante 20 mum redditae



mihi fuerunt, quibus tamen antea rescripsissem nisi per dies aliquot ferias atque otium mihi ipse indixissem firmandae valetudinis causa, cui cum studijs nostris minus bene convenit quam vellem. Praecepta artis perspicillariae tam laetus accepi, quam cupidè expectaveram, quae si feliciter effecta reddere potuero, et lentes tam accuratas nitidasque expolire, quam sunt eae quas in tubo D. Edelherij insertas vidi, puto me, inventum telescopiorum quousque licet promovere posse. Verum omnino tubis longioribus opus esse comperi, neque unquam fieri posse ut tubo brevi multum augeantur visibilia simulque lucida conspiciantur, etiamsi Hyperboles aut Ellipsis figuram vitra recipiant. Obscuritatem enim inducit augmentum necessario, eaque obscuritas rursus amplitudine aperturae lentis exterioris corrigitur; Verum nullae lentes aperturam valde magnam patiuntur, et Hyperbolicae nihilo forte majorem quam sphaericae propter incommodum colorum, hi namque inde proveniunt quod versus margines lentis cujuscunque sensim majori angulo superficies inclinantur. Videris autem circa lentes sphaericae figurae paulo iniquius sentire, cum nihil perfecti earum ope assequturos nos existimas, quae tamen nisi essent, nihil ad hunc usque diem effectum fuisset. Imo vero non multo Hyperbolicis deteriores esse arbitror ejusque opinionis rationem reddam in tractatu eo quem nunc prae manibus habeo. Sed illud interea declarandum est quo sensu dixerim in lentibus pro concursus puncto tale inveniri ultra quod nullus radius conveniat cum lentis axe.

Verum est, omnem radium axi parallelum si modo lentem penetret cum axe ipsi convenire, sed hoc nullo modo dictis meis adversari, ex figura hic adscripta facile intelliges. Radij AB, DE axi NH sunt paralleli. Quorum AB cum axe concurrit in puncto C; sed DE in puncto F, paulo ulterius quam C, quia axi propinquior sertur, nam hoc demonstratum habeo, atque ita quo propiores axi sunt radij

[p. 225]

incidentes eo cum axe semper conveniunt ulterius; Sed hic jam unum punctum determinatum est puta K, ultra quod nullius radij concursus pervenire potest, idque punctum focum lentis esse manifestum est, et quomodo inveniatur superioribus literis¹⁾ tibi nisi fallor ostendi. Similiter si radij exeant è puncto aliquo axis ut L, ij rursus punctum concursus alicubi habebunt ut M, determinatum videlicet eo modo quo punctum K. Sed ut hoc accidat oportet, distantiam LH majorem esse quam OK, hoc est quam distantia puncti concursus parallelorum à lente. Nam si radij procedant à puncto N, et sit NH brevior quam OK, non convenient ij cum axe post lentem, sed ita ferentur post refractionem quasi ex puncto aliquo magis remoto prodeuntes ut P. Et horum quoque punctorum locos facile per nova problemata mea invenio. Porro quod sensibilem tibi latitudinem obtinere haec concursus puncta videntur, nescio unde id conjicias, nisi forte spatium illud in quo lens soli opposita comburit pro latitudine puncti concursus habueris radiorum parallelorum. Ita vero nequaquam aestimari convenit, quum spatium istud latitudinem accipiat ex angulo sub quo sol nobis apparet. Quod adeo verum est, ut si lentem haberemus quae combureret ad distantiam pedum 100, ejus focus propemodum pedalis latitudinis futurus esset; ac propterea nequaquam calidus, nisi lens ipsa mirificae magnitudinis existeret. Contra verò quam planè insensibilem amplitudinem habeat punctum concursus radiorum parallelorum vel qui ex uno aliquo puncto prodierunt, demonstrat pictura per lentem convexam in cubiculo obscuro nitidissima, si modo lentis superficies non nimis magnam superficiei sphaericae portionem complectantur. Quae certè pictura nequaquam tam subtilis contingeret, nisi qui ab uno puncto venerunt radij in alio quam proximè congregarentur. Sed et numeris haec saepe examinavi, quibus solis percipi potest quantum ab accurata ratione ista distent, oculis vero non facile. Quod proportionem refractionis vitri determinas eam quae est 20 ad 13 sive 600 ad 390, quam ego scripseram 600 ad 397, credo equidem accuratis observationibus usum te fuisse, sed mihi omnium certissimae videntur, quae ex coloribus iridis habentur. Nempe sicut ex angulis semidiametri iridis caelestis utriusque Cartesius aquae refractionem invenit verae proximam; Ita ego comparato mihi exiguo cylindro vitreo minimi digiti crassitudinem habente, soli eum exposui, observavique instrumento Geometrico sub quo angulo color ruber appareat. Et sic comperi semidiametrum maximam iridis primariae in pluvia vitrea fore circiter graduum 21.50. secundariae minimam graduum 89. atque inde porro non tabularum ope quas ad modum Cartesii construere longum esset sed per regulas quasdam refractionis proportionem eam reperi qualem paulo antea statui. Quoniam verò perutiles eae regulae sunt ad aliorum quoque diaphanorum refractiones indagandas, etiam liquidorum si sphaerulas vitreas ijs impleverimus, gratiam àbs te initurum me puto, si hic eam adscripsero. ego certè cum invenissem, non parum gavisus sum. Cognito

1) La lettre N^o. 135.

[p. 226]

igitur praecedenti experimento angulo sub quo semidiameter maxima iridis primariae appareat (imaginariae tamen, namque ex una gutta de tota iride pronunciamus) sic procedendum est. Inveniatur numerus qui ductus in quadratum suum multatum¹⁾ triplo quadrato tangentis dimidij anguli ejus sub quo semidiameter iridis maxima conspicitur, fiat aequalis quadrato ejusdem tangentis ducto in²⁾ duplam secantem suam. Hoc autem invenire solidum est atque expediri potest vel per Cardani Regulam vel commodius per methodum Vietae, problemate 11 de numerosa potestatum affectarum resolutione. Repertus porro numerus dictae secanti addatur; et sicut haec summa ad radium qui est in canone ita sit radix quadratica educta ex quadrato ejusdem summae et triplo quadrato radij ad alium numerum. Is ad ipsum radium habiturus est proportionem eam quae est Refractionis. Contra vero proportione refractionis datâ, invenitur semidiameter iridis ope regulae hujusmodi quae priori facilior est. Ut minor proportionis terminus ad majorem ita sit radius circuli qui est in canone ad alium numerum. Ejus numeri quadratum auferatur à quadruplo quadrato radij, et ex residui triente eliciatur radix quadrata. dein ut major proportionis terminus ad minorem ita sit radix inventa ad alium numerum, et quaeratur cujus anguli sinus sit hic numerus. Nam si ab anguli hujus duplo auferatur angulus cujus sinus est radix praedicta, reliquum bis sumptum dabit angulum semidiametri iridis quaesitum. Habes quae pertinent ad methodum qua ego refractiones metior, et velim nihilominus vestram quoque lubenter doceri, quae si eadem est quam Cartesius in Dioptricis tradidit, scito breviori constructione ipsum uti potuisse. Nam translato in charta triangulo ipsius BPI, ducenda tantum est



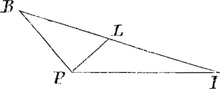PL ipsi PB ad angulos rectos, et habebitur proportio refractionis PI ad IL, neque hujus longa demonstratio est, sed cui tamen scribendae supersedere volo, ne molestus sim. Illam autem lentem ex sphaericis superficiebus talem confici posse ut radios ad datum punctum tendentes in alio puncto dato omnes colligat accuratè, ejus demonstrationem habeo evidentissimam, verum haec à reliquo tractatu seorsim tradi nequit. Autores quatuor vitrorum expoliendorum quos nominasti omnes jam ante legeram, sed tu paucis paginis multo plura comprehendisti atque utiliora pro quibus non tantum agere gratias sed et referre si quà potero paratus sum. Libelli mei exemplar alterum in locum deperditi mitto ut denuo ubi commodum erit ἐξετασιν istam perlegas. Vellem otij plus tibi suppetere, cujus tamen cum subinde particulam nancisceris, memineris nihil mihi literis tuis magis acceptum esse. Vale.

1) ‘Multatum’ signifie: ‘diminué de’.

2) ‘Ducto in’ veut dire: ‘multiplié par’.