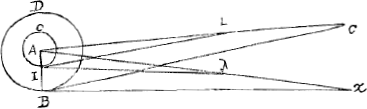
Esto angulus ABX aliquanto minor vel major recto ut hic, et sit BX aequalis peripheriae circuli DB; igitur ductâ IL parallelâ BX, erit ea aequalis peripheriae circuli OI, idque semper continget. Quamobrem concludimus rursus triangulum ABX aequari circulo DB. quod tamen falsum est. An dicemus igitur angulum ABX debuisse esse rectum; atqui hoc nusquam determinatum est Cavallerii principio, et non ita facile liquet, quid sit in causâ nisi respicias ad inscriptionem parallelogrammorum.
In sequenti exemplo pene ipse deceptus fui; est autem tale. Sit parabola ABC,
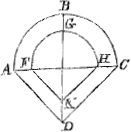
et super eadem basi triangulum isosceles ADC, habens ex hypothesi duo crura AD, DC aequalia circumferentiae parabolicae ABC. Porro sit eodem axe descripta parabola minor FGH. priori similis, et eadem basi triangulum FKH simile triangulo ADC. erit itaque circumferentia FGH aequalis cruribus FK, KH; idque eveniet semper. Igitur spatium ABC aequale est triangulo ADC. Quare ex converso si triangulum ADC aequale est parabolae ABC; erunt duo crura AD, DC simul aequalia circumferentiae ABC; atque ita facile inveniretur linea recta circumferentiae parabolicae aequalis, nisi haec omnia falsa essent. quod quidem facilius evincere est, quam veras causas erroris indicare quidem.
Plurima hisce similia afferre possem quae animadversa me ita cautum reddidere ut non facile ejusmodi demonstrationibus imposterum crediturus sim, nisi manifeste appareat eas facile commutari posse in eas quae sunt per absurdum, et fallere nesciunt. Quid tibi videatur cum de hisce tum de Theorematis meis paucis quaeso rescribe, vel si hoc non vacat saltem te valere scribito, et vale.