De bouwstenen van de schepping

Een zoektocht naar het allerkleinste

[p. 225]

27 Het zwarte gat

De situatie in de supersnaartheorie dreigde nogal ondoorzichtig te worden: trillende supersnaren zouden niet alleen de elementaire deeltjes, maar ook onze ruimte en tijd zelf hun structuur moeten geven. Hebben we ons zo ver in de wereld van het volmaakt onbekende gestort dat we door onzin worden verstrikt? Begraven we onszelf onder zo veel vragen dat we voor de wetenschap als verloren mogen worden beschouwd? Heeft het nog wel zin naar een Theorie van Alle Krachten te zoeken in deze vreemde wereld van de Planckgetallen? De titel van dit hoofdstuk doet u wellicht het ergste vermoeden.

Niets prikkelt onze nieuwsgierigheid meer dan het onbegrijpelijke. Wat zo merkwaardig is aan de wereld van de Plancklengte is dat er geen enkel model gevonden is dat een sluitend voorschrift geeft voor de gedragingen van deeltjes wanneer ze elkaar met zo sterke zwaartekrachtsvelden beïnvloeden. Dus zelfs al zouden we experimenten kunnen doen met deeltjes die de Planckmassa hebben, dan zouden we niet weten hoe de uitkomsten met theorieën vergeleken moeten worden. Er is dus werk te doen voor de natuurkundigen: maak een theorie. Wat deze theorie zal doen met de heel sterke zwaartekrachtsvelden kan ons niet zoveel schelen. Wel staan er een heleboel vereisten op ons verlanglijstje die het creëren van zo'n theorie zo moeilijk maken.

De theorie moet natuurlijk in de allereerste plaats wiskundig nauwkeurig zijn en precieze berekeningen mogelijk maken onder alle omstandigheden waarin deeltjes elkaar tegen kunnen komen. We krijgen dikwijls brieven van amateurnatuurkundigen die ons heel aardige ideeën proberen aan te praten waar we echter niets aan hebben omdat de voorschriften niet de strengheid hebben waaraan we in het vak inmiddels gewend zijn.

Ten tweede willen we uiteraard dat in onze theorie de zwaar-

[p. 226]

tekracht op zodanige wijze wordt gehanteerd dat er overeenstemming is met de formulering ervan in de algemene relativiteitstheorie van Einstein. We weten dat de zwaartekracht van grote lichamen zoals sterren en planeten heel nauwkeurig aan deze theorie gehoorzaamt. Onze nieuwe theorie moet hierbij aansluiten.

Ten derde weten we dat de wetten van de quantummechanica onverbiddelijk zijn. We willen dus ook dat onze theorie binnen het raam van de quantummechanica kan worden geformuleerd.

Zowel de quantummechanica als de relativiteitstheorie heeft de eigenschap dat als je ook maar de geringste afwijking van hun principes toestaat er een totaal andere theorie ontstaat die in niets meer lijkt op wat we weten van de natuur. ‘Een beetje quantummechanisch’ of ‘een beetje relativistisch’ zijn net zomin mogelijk als ‘een beetje zwanger’. Wel is het denkbaar dat ofwel de quantummechanica ofwel de relativiteitstheorie ofwel beide een te eng raamwerk zullen zijn voor de nieuwe theorie, dus dat je de principes verder moet uitbreiden. Maar negeren kun je ze niet. Ik zal u niet te veel vermoeien met pogingen theorieën uiteen te zetten die we zelf niet begrijpen, maar ik wil wel aangeven welke wegen er nog zijn die verder bewandeld kunnen worden.

In het heelal bevinden zich sterren met een massa die aanzienlijk meer is dan die van onze eigen ster, de zon. Daardoor is de zwaartekracht aan de oppervlakte aanzienlijk sterker dan op aarde of op de zon. De enorme hoeveelheden materie in zo'n ster veroorzaken in zijn binnenste een onvoorstelbaar hoge druk. Alleen doordat de temperatuur daarbinnen ook gigantisch is, is de tegendruk binnenin voldoende om de ster tegen ineenklappen te behoeden.

Echter, de ster verliest warmte. Eerst vinden er nog allerlei zeer energierijke kernreacties plaats die de temperatuur hoog genoeg houden en zelfs doen toenemen, maar de nucleaire

[p. 227]

brandstof raakt vroeg of laat op. Hoe zwaarder de ster, des te hoger de druk en de temperatuur, en des te sneller wordt de nucleaire brandstof verbruikt. Dan wordt de tegendruk minder en het binnenste van de ster ‘bezwijkt’ onder de druk. Door het kleiner worden neemt de zwaartekracht in sterkte alleen maar toe en een implosie (een plotseling ineenklappen) kan dan niet meer uitblijven.

Meestal ontstaat er bij deze implosie nog zo veel hitte dat een groot deel van de buitenste schil van de ster door de stralingsdruk wordt weggeblazen. Dan kan de implosie nog tot staan worden gebracht en blijft er een uiterst compacte bol van ‘kernmaterie’ over: een zogenaamde neutronenster. Deze neutronenster vertoont vaak een zeer hoge draaisnelheid (tot ongeveer duizend omwentelingen per seconde), en onregelmatigheden op het oppervlak veroorzaken dan een snel pulserend radiosignaal. Dit radiosignaal was waaraan men deze objecten het eerst ontdekte en ze heten daarom ook wel ‘pulsars’. In de astronomische tabellen worden pulsars aangeduid met de lettercombinate ‘lgm’. Dit stamt uit de tijd dat men nog dacht aan de mogelijkheid dat deze vreemde pulserende signalen van een buitenaardse beschaving afkomstig waren: ‘Little Green Men’.

Als er niet voldoende materiaal van de buitenste schil is weggeblazen of als er weer nieuwe materie op de pulsar terecht komt, is ook deze compacte materiebol niet meer tegen de druk bestand. De berekeningen van de astronoom-natuurkundige Subrahmanyan Chandrasekhar tonen onweerlegbaar aan dat als de massa van een compact, afgekoeld object meer is dan enkele zonsmassa's er geen enkele soort materie bestaat die zo veel druk kan weerstaan. De zwaartekracht wordt nu zo sterk dat alleen Einsteins relativiteitstheorie precies kan vertellen wat er gebeurt. Doordat de zwaartekracht collectief werkt op alle deeltjes in de ster en voor deeltjes afzonderlijk nog heel zwak is, hoeven we nog niets te weten omtrent de ‘quantum-zwaartekracht’ om toch al heel precies de gebeurtenissen te

[p. 228]

kunnen voorspellen. De ons bekende natuurwetten zijn daartoe volledig toereikend. We koesteren geen enkele twijfel omtrent de uitkomst van deze berekening.

De uitkomst is een ‘zwart gat’. Een zwart gat ontstaat wanneer de ineenstortende materie op zeker moment de lichtsnelheid bereikt. Er wordt dan een grens overschreden, een ‘point of no return’. Een (onfortuinlijke) ruimtereiziger die met deze ineenstortende materie mee naar binnen gaat, kan op dat moment niet meer terug, ongeacht de sterkte van de motoren van zijn ruimteschip, want zelfs als hij ter plekke met de lichtsnelheid zou omkeren, zou hij er niet in slagen te ontsnappen. Ook alle signalen die hij dan verstuurt, komen niet meer naar buiten.

Als men dit alles op veilige afstand zou gadeslaan zou men weldra geen enkel signaal meer van de invallende materie en de mee naarbinnen vliegende ruimtereiziger kunnen detecteren. Het object wordt zwart, vandaar de naam ‘zwart gat’. Omdat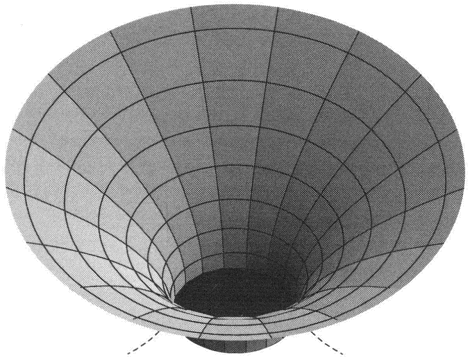

Figuur 29. De gekromde ruimte-tijd nabij een zwart gat (fantasieweergave).

[p. 229]

een zwart gat uiteindelijk niets anders is dan een bal ‘pure zwaartekracht’ kunnen zijn eigenschappen met wiskundige precisie worden berekend. Slechts drie getallen zouden er nodig zijn om een gegeven zwart gat volledig te karakteriseren: zijn massa, zijn impulsmoment (draaibeweging) en zijn elektrische lading.

Wat we verder precies kunnen uitrekenen, is hoe bundels elementaire deeltjes zich gedragen als zij zich dicht bij een zwart gat wagen. Stephen Hawking bestudeerde dit rond 1974. Hij stuitte op een moeilijkheid die in het begin op een formaliteit leek. Wanneer precies noem je iets nu een deeltje, en wanneer is het slechts een bij drage tot de structuur van de lege ruimte? Wat voor een onderzoeker die bezig is in het gat te vallen op lege ruimte lijkt, blijkt voor een buitenstaander deeltjes te bevatten die nog net op het nippertje aan het zwarte gat konden ontsnappen. Een ongerijmdheid in de theorie? Dit is wat hij eerst dacht,maar hoe hij de berekening ook deed, er bleef altijd een stroom deeltjes over die ontsnappen. En toen deed hij de ontdekking die ik nog steeds als zijn allerbelangrijkste beschouw. Die deeltjes zijn echt! Ieder zwart gat zendt een constante stroom deeltjes van alle soorten uit.

De intensiteit van deze deeltjesemissie is omgekeerd evenredig met het kwadraat van de massa van het zwarte gat. Voor zwarte gaten waarover de sterrenkundigen het hebben is deze emissie zo uiterst zwak dat zij altijd overstemd wordt door al datgene wat er in het gat valt, zelfs als het ver verwijderd is van andere sterren of sterrenstelsels. Maar nou gaat het even om het principe: er kan iets uit een zwart gat komen, en het komt er spontaan uit.¹

1 De deeltjes die uit een zwart gat komen volgen de statistische wetten van warmtestraling. Het zwarte gat heeft een bepaalde temperatuur, en de straling is als die van een sneeuwvlok, gloeilamp of als die van een ster. Er zullen dus zeer beslist géén kleine groene mannetjes of ruimtevaarders uit een zwart gat kunnen komen!

[p. 230]

Dit betekent dat een zwart gat massa kan verliezen en dus lichter zou kunnen worden dan de kritische massawaarde die Chandrasekhar berekend heeft. En hoe lichter het zwarte gat is, des te sneller het nog meer massa verliest. Een snelle berekening leert dat als het zwarte gat een massa heeft van een kleine berg het nog maar luttele seconden nodig heeft om al zijn massa in de vorm van straling naar buiten te slingeren. Dat zou een heel wat intensievere explosie geven dan de krachtigste kernbom! Nu suggereerde ik misschien dat ook deze berekening uitsluitend gebruikmaakt van geheel bekende natuurwetten en daarom onaanvechtbaar is. Om twee redenen is dat niet helemaal waar.

Ten eerste hebben we nog nooit een zwart gat van nabij kunnen bestuderen en zeker niet een zwart gat dat zo klein is dat zijn Hawkingstraling zou kunnen worden gedetecteerd. We weten zelfs niet of zulke kleine zwarte gaten in het heelal aanwezig zijn of slechts een uiterst onwaarschijnlijke zeldzaamheid. Zelfs al denken we de theorie te kennen dan had het geen kwaad gekund als deze op een of andere manier getoetst kon worden. Het effect dat Hawking ontdekte is wel degelijk een quantumeffect. Gebeurt alles wel zoals we nu denken dat het gaat?

En dan kom ik op mijn tweede punt. Ik kan me namelijk een theorie voorstellen die een ander resultaat geeft. Toen ik hier voor het eerst in geïnteresseerd raakte en naar een volledig sluitende beschrijving van zwarte gaten zocht, probeerde ik verschillende alternatieve theorieën te construeren. En ik kon een theorie formuleren die een andere uitkomst geeft dan de berekening van Hawking: het zwarte gat zou aanzienlijk intensiever kunnen stralen dan Hawking aangaf. Toegegeven, je krijgt die afwijkende uitkomst alleen als je de wetten van de quantummechanica bij een zwart gat op een andere manier hanteert dan overal elders, maar ik meen dat er geen absoluut bewijs bestaat dat dit niet ‘mag’.

[p. 231]

Stephen Hawking kende ik inmiddels van diverse conferenties en workshops. Het is onbegrijpelijk hoe hij zijn zware lichamelijke handicap trotseert en een belangrijke rol kan blijven spelen in de hedendaagse theoretische natuurkunde.¹ Nu kan hij uitstekend met ons blijven communiceren dankzij een ingenieuze spraakcomputer die hij met zijn wijsvinger bedient. Met die wijsvinger heeft hij mij bijna, maar toch niet helemaal kunnen overtuigen dat mijn alternatieve theorie niet houdbaar is. Nu ik verder heb gewerkt aan de zwarte gaten geloof ik wel dat zijn berekening de werkelijkheid juist weergeeft. Ik weet het alleen niet zeker.

Er is echter een veel belangrijker aspect aan deze Hawkingstraling verbonden. Het zwarte gat wordt steeds kleiner en de straling steeds intensiever. Vlak vóór het einde zal de afmeting vergelijkbaar worden met de Plancklengte, het zwarte gat zal een massa hebben die weinig meer is dan de Planckmassa en ook de energie van de uitgezonden deeltjes zal met de Planckmassa corresponderen. Alleen een volledige theorie van de quantumzwaartekracht kan precies voorspellen en beschrijven wat er daarna met een zwart gat zal gebeuren!

Ziedaar het belang van zwarte gaten voor onze theorie van elementaire deeltjes bij de Plancklengte. Zwarte gaten zouden een ideaal laboratorium kunnen zijn voor gedachte-experimenten. Zij bereiken helemaal uit zichzelf het energiegebied rond de Planckenergie. Een goede theorie moet ook hier kunnen vertellen hoe je rekenen moet. En de snarentheorie dan? Volgens de snarentheoretici hadden zij een volledige theorie van alle natuurkrachten, en dus zou hun theorie ondubbelzinnig uitsluitsel moeten geven omtrent de vraag hoe een zwart gat explodeert. Terwijl in de jaren tachtig de snarentheoretici aan

1 Zie Stephen Hawking, Het heelal. Verleden en toekomst van ruimte en tijd. Amsterdam, Bert Bakker, 1988. Oorspronkelijke titel A Brief History of Time. New York, 1988.

[p. 232]

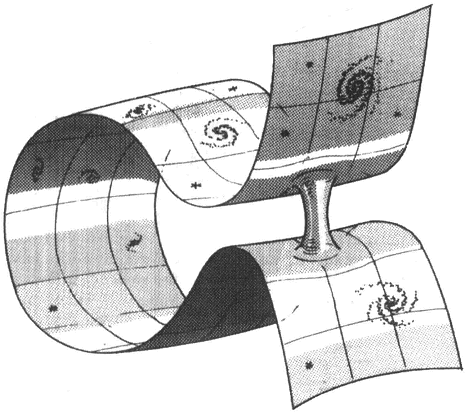
Figuur 30. Een wormgat kan verafgelegen gedeeltes van een heelal verbinden.

de wereld verkondigden dat zij de Theorie van Alles op het spoor zaten, was ik zelf begonnen zwarte gaten te bestuderen. Stephen Hawking beweerde dat zwarte gaten doorgeefluikjes zijn naar andere universums, en dat daarom alles wat er uit een zwart gat komt fundamenteel onberekenbaar is (zie figuur 30). Een theorie zonder voorspellingen?

Ik begon hoe langer hoe sterker het vermoeden te krijgen dat noch Hawkings theorie, noch supersnarentheorie hier het correcte antwoord kunnen geven! Die theorieën waren namelijk ten eerste in strijd met elkaar, en ten tweede in strijd met mijn

[p. 233]

overtuiging dat de Hawkingstraling uit de horizon van een zwart gat komt alsof die een soort huid is die de deeltjes uitademt. Als ik de snarentheoretici hiermee confronteerde kreeg ik een ontwijkend antwoord: hun theorie was ongetwijfeld correct, maar omdat deze vraag nu eventjes te moeilijk was waren zwarte gaten niet interessant voor hen.

Waar de theorieën met elkaar overhoop lagen, was de vraag hoe je de ‘soorten’ zwarte gaten tellen moet. Enerzijds leek het dat ze een rangnummer hebben dat qua grootte precies op de horizon past (zie figuur 31), anderzijds leek het erop dat ze strikt ontelbaar zijn. Hoe moet je zwarte gaten tellen, en hoe karakteriseer je hun rangnummer?

Neem nou een zwart gat, dat zijn leven misschien is begonnen als een groot ‘astronomisch’ zwart gat, en dat nu zijn leven explosief beëindigt. Hoe langer je erover denkt, hoe belangrijker de rol van zwarte gaten in de wereld van het uiterst kleine eruit gaat zien. Mijn uitgangspunt was nu: als je echt wilt begrijpen hoe de zwaartekracht werkt op individuele deeltjes, wat kun je dan beter als gedachtelaboratorium nemen dan het ‘sterkst mogelijke zwaartekrachtsveld’? Als je deeltjes wilt lokaliseren met meer dan de precisie van een Plancklengte, krijgen ze een energie die correspondeert met meer dan de Planckmassa. Maar dan worden het kleine zwarte gaatjes, met afmetingen van méér dan een Plancklengte.

Dit is de moeilijkheid die we al eerder noemden: door het bobbelen van de ruimte-tijd wordt het onmogelijk posities nauwkeuriger te bepalen dan de Plancklengte! Als er een einde komt aan onze speurtocht naar het kleine, dan is dat bij het kleinst mogelijke object: een mini-zwart-gat. Ruimte en tijd verliezen dan hun gebruikelijke betekenis, maar wat ervoor in de plaats komt begrijpen we niet. Onze speurtocht lijkt letterlijk en figuurlijk bij een zwart gat te zijn geëindigd.

[p. 234]

Figuur 31. Als we de quantumtoestanden van een zwart gat rangnummers zouden geven, zouden die nummers, met cijfers van ongeveer 10^-33 cm grootte, net op hun horizon passen (grote zwarte gaten kunnen dus heel veel quantumtoestanden hebben).