De bouwstenen van de schepping

Een zoektocht naar het allerkleinste

[p. 133]

14 De magnetische monopool

Het probleem van de permanente quarkopsluiting ging mij in 1973 en 1974 steeds meer boeien. Wat we wisten, was alleen dat de kleurkrachten die de naakte quarks op heel kleine afstand van elkaar uitoefenen relatief kleiner zijn dan de kleurkrachten tussen aangeklede quarks op grotere afstand. Dat was het effect van de ‘negatieve afscherming’ waarover ik het had in het vorige hoofdstuk. Extrapoleer je dit naar nog grotere afstand, dan lijkt het aannemelijk dat de kleurkrachten tussen quarks op grotere afstand van elkaar nog weer veel sterker worden. De krachten zouden gemakkelijk zo sterk kunnen worden dat ze de quarks permanent bij elkaar houden. Maar gebeurt dat nu ook? De essentiële moeilijkheid was hier dat juist omdat de krachten zo sterk zijn, berekeningen bijna onmogelijk werden. Het enige wat we goed kunnen, is rekenen aan deeltjes die bij benadering rechtuit gaan. Dat zullen de quarks zeer beslist niet doen als de krachten zo groot zijn. Dus de vraag werd: kun je nu nog een fundamentele reden aangeven waarom quarks altijd onzichtbaar blijven? Waarom vormen de veldlijnen van de kleurijktheorie worstjes zoals figuur 14, zonder uit te waaieren zoals ‘gewone’ elektrische en magnetische velden? Als je dit kunt verklaren, kun je misschien ook een rekenmethode vinden om alle eigenschappen van de hadronen te verklaren. Ik probeerde van alles om het antwoord te ontdekken.

Maar Holger Nielsen en Poul Oleson uit Kopenhagen, en onafhankelijk van hen Bruno Zumino van cern, ontdekten iets waar ik helemaal niet aan had gedacht. Beschouw eens een stukje supergeleidend materiaal, zeiden ze. Probeer daar nu eens een magnetische monopool in te stoppen. Deze bestaan weliswaar niet, maar je kunt je deze in gedachten voorstellen, en dan uitrekenen wat de supergeleider dan zou doen. Een monopool is een hypothetisch deeltje dat, anders dan een ge-

[p. 134]

wone magneet, wél een magnetische noordpool bezit maar niet de bijbehorende zuidpool (of juist andersom). Monopolen zijn nog nooit gevonden, maar daarover straks meer.

Ik had eerder uitgelegd dat een supergeleider geen enkel elektrisch of magnetisch veld tolereert: het schermt de velden volledig af. Maar dat kan hij niet met het magnetische veld van een monopool. Om een monopool toe te laten moet de supergeleider een gebiedje creëren waar het materiaal niet meer supergeleidend is, en daar mag het magnetische veld van de monopool dan doorheen lopen. Als je dit verder doorrekent vind je dat de veldlijnen tussen een magnetische noordpool en een magnetische zuidpool precies de worstvorm krijgen van figuur 14. Binnen het worstje is het materiaal niet meer supergeleidend. Omdat dit extra energie kost tracht het materiaal dit gebiedje zo klein mogelijk te houden, vandaar dat de veldlijnen niet uitwaaieren. (Zie ook figuur 14a.)

En zo kregen Nielsen, Olesen en Zumino een model voor quarks. Quarks zijn een soort magnetische monopolen, en onze ruimte is een soort supergeleider. Dit hadden we al eerder gezien: een Higgstheorie!

Jammer alleen dat je nooit staande kon houden dat quarks werkelijk magnetische monopolen zouden zijn. Volgens de quantumchromodynamica, waar ik inmiddels heilig in geloofde, hebben quarks echt niets dat op magnetische lading lijkt. En stel nou dat je die quantumchromodynamica even vergat en de theorie van magnetische monopolen ter hand nam. Er bestond nog geen enkele bruikbare theorie om hun bewegingen nauwkeurig te beschrijven, omdat magnetische monopoollading altijd heel sterk moest zijn. Als je die lading stopt in puntvormige deeltjes zoals de quarks dan zouden de krachten ertussen altijd groot moeten zijn, ook van dichtbij. In zo'n theorie kun je niets meer uitrekenen, en we raken dus van de wal in de sloot.

Maar het idee boeide me wel. Laten we eens kijken, dacht ik, wat er gebeurt als je dit voor een Yang-Millssysteem doet. En

[p. 135]

toen deed zich een merkwaardige moeilijkheid voor. De fluxbuizen, zoals ik de worstjes ging noemen, werden instabiel. Maar hoe kon dat nou, want de magnetische veldlijnen van magnetische monopolen mochten alleen en uitsluitend uitkomen bij andere monopolen. Als er geen fluxbuis meer is, hoe lopen de veldlijnen dan? En toen leerde ik iets heel belangrijks van dit gedachte-experiment. De fluxbuizen vielen uit elkaar doordat in het model dat ik beschouwde zich spontaan nieuwe noord- en zuidmonopolen hadden gevormd. Maar niemand wist nog dat die konden ontstaan in zulke modellen!

Vergeet weer even het quarkopsluitingsprobleem. Het model dat ik aan het bekijken was had eigenlijk niets meer met de sterke kracht te maken. Ik was onbedoeld weer uitgekomen bij de zwakke-interactietheorie. Daarvan waren er in 1974 nog allerlei varianten in omloop. Ik kon afleiden dat in sommige van die modellen, met name één dat was bedacht door Glashow en een jongere medewerker van hem, Howard Georgi, magnetische monopolen konden ontstaan. Je kon ze als het ware construeren uit de bouwdoos van velden en deeltjes in zo'n theorie. In tegenstelling tot alle oudere ideeën over ‘puntvormige’ magnetische monopolen waren de monopolen die ik nu kon construeren heel ‘zachte’, ruimtelijk uitgestrekte objecten. Ik kon er allerlei eigenschappen van uitrekenen, inclusief de massa ervan. Dat dit alles nog niet eerder opgemerkt was kwam mede doordat de energie, ofwel massa, van deze nieuwe objecten veel groter is dan die van alle ‘gewone’ deeltjes. Dit was een interessante ontdekking, die ik in een grote conferentie over elementaire deeltjes in Londen uiteenzette. Daar bleek me toen dat de ontdekking onafhankelijk van mij ook in Moskou was gedaan door Alexander Polyakov, in een discussie met Lev Okun.

Nu was de principiële mogelijkheid van losse magnetische pooldeeltjes al in 1931 geopperd door Paul Dirac. Hij bewees op heel algemene gronden dat het product van de fundamentele elektrische lading van het elektron en de fundamentele mag-

[p. 136]

netische lading van een eventuele magnetische monopool altijd een veelvoud moet zijn van de constante van Planck. Dat is een beetje vervelend als je een model van een magnetische monopool wilt construeren, want hier volgt uit dat de magnetische lading van een monopool zo sterk is dat je deze nooit storingstheoretisch kunt beschrijven. De magnetische eenheidslading blijkt dan namelijk 68,5 maal zo sterk te zijn als de elektrische eenheidslading (dat getal is precies de helft van het beroemde getal 137,036..., zie ‘de elektromagnetische kracht’, op pagina 36). Als quarks monopolen waren, zouden ze nooit asymptotisch vrij kunnen zijn!

Natuurlijk waren er allerlei onderzoekers geweest die niettemin toch geprobeerd hadden monopolen storingstheoretisch te behandelen, met zeer ontmoedigende resultaten. Maar mijn monopool was geen puntdeeltje maar een ‘hoopje veld’. Een storingstheoretische benadering die alleen maar goed zou zijn voor kleine magnetische ladingen had ik niet nodig en daarom werd mijn monopool¹ veel mooier. Wat zeer belangrijk was, was dat ik de massa ervan precies kon uitrekenen en dat was in alle vorige pogingen nooit mogelijk geweest. Als dit Georgi-Glashowmodel goed was dan zou de magnetische monopool ongeveer 8000 keer zo zwaar zijn als het waterstofatoom.

Benjamin Lee was zeer onder de indruk. Toen ik in Londen mijn werk met hem stond te bespreken, kwam er iemand langs die enigszins verbaasd aan mij vroeg: ‘Hé, heb jij nu ook al een model voor een magnetische monopool?’ Benjamin antwoordde daarop: ‘Hij heeft geen model, hij heeft er een gevónden!’ Ik mocht Benjamin erg graag. Het was een groot gemis voor de wereld van de deeltjesfysica toen hij een aantal jaren later, veel te jong, door een tragisch verkeersongeval van deze wereld werd weggenomen.

Bevatte het Georgi-Glashowmodel een monopool, het Wein-

1 Ik zeg wel ‘mijn’, maar hij is deels van Polyakov en Okun.

[p. 137]

berg-Salammodel bevat er helaas geen. In dit model is er nog een technische obstructie die monopolen niet toestaat, tenzij je er verdere veranderingen in aanbrengt. En het Weinberg-Salammodel ging het winnen van het Georgi-Glashowmodel en andere modellen als je naar de experimentele resultaten keek. Als er magnetische monopolen bestaan, zullen ze niet de massa hebben zoals zou volgen uit het Georgi-Glashowmodel, zo'n 8000 maal de protonmassa, maar veel en veel zwaarder. Daarover straks meer.

Deze theoretische ontwikkeling had in ieder geval tot gevolg dat experimentatoren met hernieuwde energie naar magnetische monopolen gingen zoeken, in water, in maangesteenten, en in oesters.¹ Er werden zeer gevoelige detectoren met supergeleidende spoeltjes gebouwd. Een enkele keer meende men een signaal opgevangen te hebben, maar wanneer je de opstelling verfijnde en de detectie-efficiëntie verbeterde, bleven de signalen steeds achterwege. Dit is een bekend verschijnsel bij experimenten, een teken dat het eerste signaal (dat ook door de experimentatoren zelf onbetrouwbaar was genoemd) op een onjuiste interpretatie berustte.

We weten nog steeds niet of magnetische monopolen bestaan, maar de ontdekking van de theoretische mogelijkheid zou belangrijk blijven, en wel om twee redenen. Zoals we later zullen zien, verwachten we dat het Weinberg-Salammodel slechts die deeltjes beschrijft die in onze tijd experimenteel bestudeerd kunnen worden. Maar er is een grens aan de energie die men in laboratoria aan een enkel deeltje geven kan. Bij energieën die veel en veel hoger zijn dan die grens, verwachten we nieuwe verschijnselen die slechts begrepen zullen kunnen worden als het Weinberg-Salammodel verder wordt uitgebreid. We weten nog niet hoe die verbeterde theorie eruit zal moeten zien, maar er is alle kans dat dan de ‘'t Hooft-Polyakovmono-

1 Oesters staan erom bekend dat ze vreemde mineralen uit het zeewater filteren.

[p. 138]

pool’ tot de mogelijkheden gaat behoren. Het model dat ik in hoofdstuk 23 zal beschrijven, bevat echte, maar wel superzware magnetische monopolen.

‘Wat mag, moet,’ zeggen sommige theoretici. Iedere theoretisch denkbare constructie moet ook ergens in de natuur te vinden zijn. Dat is helaas niet altijd juist, maar het geldt wel voor monopolen. Als ze namelijk theoretisch mogelijk zijn, kun je ook uitrekenen hoeveel er werkelijk ontstaan zouden zijn in de allereerste beginfasen van het heelal. De resultaten van zulke berekeningen bezorgen hoofdbrekens bij die theoretici die het begin van de kosmos willen begrijpen. Al die monopolen zouden het aanzien van het heelal anders maken dan wat we nu zien. In feite leidt men uit deze kosmologische berekeningen beperkingen af omtrent de deeltjesmodellen die monopolen zouden toestaan.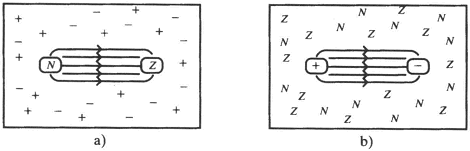

Figuur 17. a) In een supergeleider bevinden zich positieve of negatieve ladingen die zich collectief in een laagste energietoestand bevinden (‘Bose-Einsteincondensatie’). Het magnetische veld tussen een N-monopool en een Z-monopool wordt gedwongen de vorm van een worstje (‘vortex’) aan te nemen. b) In de quantumchromodynamica hebben we gecondenseerde kleurmonopolen die de hele ruimte vullen. Hierdoor wordt het kleur-elektrische veld tussen twee quarks in een worstvorm geperst.

En het tweede belang van monopolen is dat we nu gingen inzien dat in de quantumchromodynamica ook kleurmagnetische

[p. 139]

monopolen kunnen voorkomen, en zelfs in grote hoeveelheden. Als je aanneemt dat deze kleurmonopolen weer een soort Bose-Einsteincondensatie ondergaan dan krijg je het begin van een échte verklaring van het verschijnsel quarkopsluiting in de quantumchromodynamica: we gebruiken inderdaad het oorspronkelijke idee van Nielsen en Olesen (figuur 17a), maar verwisselen alle elektrische ladingen met de magnetische. De quarks zijn kleur-elektrisch; het omringende vacuüm is een kleurmagnetische supergeleider! Zie figuur 17b.

Dit is moeilijke maar zeer boeiende materie. Met de kleurmagnetische monopool leek er weer een stukje van De Grote Legpuzzel gevonden te zijn. De Nielsen-Olesenvortex en de magnetische monopool zouden slechts het begin zijn van een serie bijzondere wiskundige verschijnselen in de Yang-Millstheorieën, waar wiskundigen en natuurkundigen ook nu nog niet op uitgekeken zijn.