De bouwstenen van de schepping
(1992)–Gerard 't Hooft–Een zoektocht naar het allerkleinste
[pagina 119]
| |
13 De kleurtheorieHeel wat onoverzichtelijker en ongrijpbaarder leken nog steeds de sterke krachten. Wel leerde men met nieuwe versnellers diverse deeltjes steeds harder, met steeds meer energie, tegen elkaar aan te kogelen, waardoor men een steeds betere kijk kreeg op de merkwaardige structuur van de hadronen. Het eerste dat opviel, was dat de lijst van ‘resonanties’ steeds langer werd. Een resonantie kan men het best omschrijven als een deeltje dat in allerlei opzichten lijkt op één van de deeltjes in tabel 1. Alleen de massa is groter en meestal is de spin ook groter. Er zijn baryonische en mesonische resonanties. Zonder het totaal aan de quantumgetallen S (vreemdheid) en I3 (isospin) te veranderen kunnen ze in lichtere deeltjes uiteenvallen in zo'n 10-23 seconde. De resonanties leken in series voor te komen. De zwaardere (dus meer energetische) deeltjes in zo'n serie hebben een grote spin, dus ze draaien heftiger om hun as dan de lichtere. Stel nu eens dat ook deze resonanties opgebouwd zijn uit zoiets als ‘quarks’. De heftige draaizin (om precies te zijn: het impulsmoment) van de zwaardere resonanties zou je dan alleen kunnen begrijpen als de quarks daar in grotere cirkels om elkaar heen draaien, omdat ze zelf namelijk niet sneller mogen bewegen dan het licht. En toch worden die quarks niet van elkaar losgeschud. Zonder te pogen een antwoord op deze vraag te vinden ontdekte Gabriele Veneziano een eenvoudige wiskundige formule die op een bijzonder elegante manier de effecten van de resonanties op de botsingen tussen deeltjes weergaf. Het bijzondere van zijn formule was dat de uitwerkingen van de sterke kracht er heel realistisch in werden beschreven (dat wil zeggen, redelijk goed in overeenstemming met de experimentele gegevens), terwijl geen enkele bestaande theorie de formule kon verklaren. Nog niet. De formule zou een heel belangrijke rol | |
[pagina 120]
| |
gaan spelen en ik kom er nog op terug. Voeren we de botsingsenergie nog verder op dan komen er zo veel deeltjes en resonanties vrij (die alle onmiddellijk weer in gewone deeltjes uiteenvallen) dat deze niet allemaal meer duidelijk te onderscheiden zijn. Maar dan is er iets anders dat ook opvalt. Stel dat de sterk wisselwerkende deeltjes uit een soort geleiachtig materiaal waren gemaakt. Als ze met zeer veel kracht tegen elkaar aangesmeten worden, zou je verwachten dat ze elkaar weliswaar volledig vernielen, maar dat de brokstukken ongeveer in dezelfde richting door zouden gaan, in de voorwaartse richting dus. Dat gebeurt ook vaak. Echter, wat de experimentatoren ontdekten, is dat soms ook brokstukken met grote kracht in zijwaartse richting worden gegooid. Alsof er kleine harde pitjes in die gelei zitten! James Bjorken ontdekte dat die zijwaartse beweging dan aan enige simpele vergelijkingen gaat voldoen: de botsingsprocessen bij heel hoge energie en iets minder hoge energie gaan steeds meer gelijkenis vertonen. Men ging dit ‘het schaalgedrag van Bjorken’, ofwel Bjorken scaling noemen. Feynman was geïntrigeerd door dit verschijnsel. Bjorken-scaling zou je namelijk wél met een ‘gewone’ veldentheorie kunnen begrijpen. Neem nou eens aan dat de resonanties uit fundamentele bouwsteentjes bestaan. Dat hoeven de quarks niet te zijn, waarschuwde Feynman; hij noemde ze ‘partonen’. Als je nou aanneemt dat deze ‘partonen’ zich betrekkelijk vrij binnen zo'n resonantie kunnen bewegen, dan kon je Bjorken-scaling verklaren. Quarks of partonen, vrij bewegend of onmogelijk los te krijgen? Het raadsel was compleet. Ik begreep niets van dit alles en besloot me dan ook verre te houden van de sterke kracht. En dat terwijl ik het antwoord op het raadsel van de Bjorken-scaling in mijn rekenschriften had staan! Ik had de massaloze Yang-Millstheorie goed bestudeerd, en iets opgemerkt waar ik de eerste tijd verder weinig aandacht aan besteedde. Het be- | |
[pagina 121]
| |
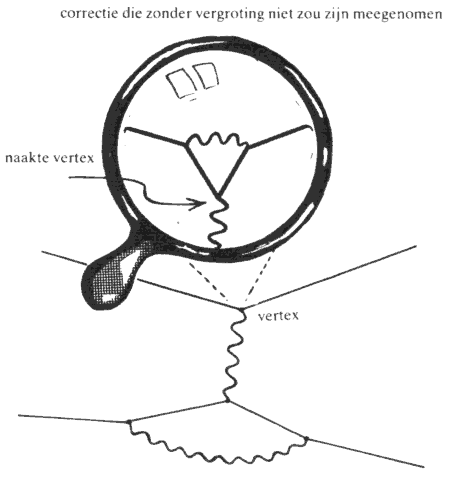
Figuur 13. De definitie van een fundamentele interactie hangt van de vergrotingsfactor af.
| |
[pagina 122]
| |
treft de schaaltransformatie, die in hoofdstuk 1 werd besproken. U weet wel, je kunt de wereld van het grote in het klein nabootsen. Sommige details gaan er dan anders uitzien, andere niet. We vinden zoiets bij de elementaire deeltjes weer terug! Als je een theorie met deeltjes onder een microscoop beschouwt dan zie je dezelfde deeltjes weer. Vooral als je geen massa had in je theorie, dan lijken de deeltjes in de microscoop heel erg veel op de oorspronkelijke. Alleen als je renormering toepast gebeurt er iets. De naakte deeltjes zijn een beetje anders dan de aangeklede deeltjes, en daarom is de interactiesterkte tussen de deeltjes een beetje anders wanneer je ze onder de microscoop bekijkt. Nu waren we van de oudere theorieën gewend dat de interactiesterkte onder de microscoop altijd sterker is dan op grotere schaal. De naakte deeltjes reageren heftiger dan de aangeklede deeltjes, omdat de deken van ‘vacuümdeeltjes’ waarin ze zich hullen de lading van de naakte deeltjes gedeeltelijk afschermt. Dat bleek bij alle veldentheorieën zo te zijn, behalve de nieuwe theorieën: de ijktheorieën gebaseerd op het idee van Yang en Mills. Daar is het net andersom, maar omdat die theorieën nieuw waren wisten de onderzoekers dit nog niet. Op nogal raadselachtige wijze wordt het naakte deeltje op zodanige wijze omgeven door Yang-Millsfotonen uit het vacuüm dat deze de lading versterken, niet afschermen. Als je haar voor het eerst uitvoert is de berekening nogal bewerkelijk, maar ik kende het verschijnsel, in 1972. Bovendien wist ik dat als de theorie behalve de Yang-Millsfotonen ook nog fermionen bevat, deze weer de andere kant op werken. Heb je meer dan 16 fermionsoorten (maar dat getal is voor verschillende ijktheorieën verschillend) dan werkt de ‘vacuümdeken’ weer als in de oudere theorie. In 1972 was er een kleine conferentie in Marseille. Op het vliegveld kwam ik Kurt Symanzik al tegen, en hij vertelde waar hij mee bezig was. Hij probeerde Bjorken-scaling te verklaren | |
[pagina 123]
| |
met een veldentheorie. Maar Symanzik zou zich nog langere tijd uitsluitend met spin-0-theorieën bezig houden, die hij als het prototype voor alle renormeerbare veldentheorieën beschouwde. ‘Als nu maar dat schaalgedrag kon worden omgekeerd,’ zei hij, ‘dan zou je een theorie krijgen waarin de deeltjes in kleine omgeving zich als vrije deeltjes gedragen, maar op grote afstand zouden ze sterke krachten op elkaar uitoefenen.’ ‘Nou,’ riep ik uit, ‘dat is precies wat je krijgt in de ijktheorieën van Yang en Mills!’ Symanzik was daar nogal sceptisch over. Ik had me vast ergens in m'n berekening vergist met een minteken, meende hij. ‘En als dat niet zo is, moet je dat resultaat snel publiceren, want dan is het belangrijk.’ Ik heb er spijt van dat ik die raad niet heb opgevolgd, maar ik was toen bezig met een ingewikkelde berekening over de zwaartekrachttheorie, en ik wist niet precies hoe ik mijn resultaat zou moeten presenteren; ik wist immers niets van de sterke kracht af. Maar ik ben Symanzik wel dankbaar. Hij eindigde zijn voordracht in Marseille met de woorden: ‘Het lijkt alsof geen enkele theorie Bjorken-scaling kan verklaren, maar misschien moeten we nog eens kijken naar de ijktheorieën.’ En zo stelde hij mij volop in de gelegenheid bij de discussie die volgde op te merken dat ik die berekening al had gedaan, waarna ik de uitkomst op het bord schreef. De eerste publicatie over het bijzondere schaalgedrag van ijktheorieën kwam van David Politzer, een jonge onderzoeker aan Harvard, en gelijktijdig van David Gross en Frank Wilczek in Princeton. Zij noemden dit ‘asymptotische vrijheid’.Ga naar voetnoot1 Het was Symanzik die iedereen die het maar horen wilde, liet weten dat ik dit resultaat veel eerder al publiekelijk had verkondigd | |
[pagina 124]
| |
tijdens de conferentie in Marseille. ‘Dat geldt, als het om de prioriteit gaat,’ zei hij. Van de grote legpuzzel die de natuur ons biedt, was dit een nog ontbrekend stukje. Andere stukjes waren al eerder gelegd. Gell-Mann had er samen met Harald Fritzsch al op gewezen dat Yang-Millskrachten bij uitstek geschikt zijn om de binding tussen quarks te beschrijven. Ook de veelzijdige Japanner Yoichiro Nambu had dit idee. Je kunt dan namelijk begrijpen waarom juist hetzij drie quarks, hetzij één quark en één antiquark bij elkaar kunnen blijven zitten, en ook waarom de baryonen met spin 1½ een decuplet vormen en die met spin ½ een octet.Ga naar voetnoot1 Je hebt dan een stelsel van precies acht elektrische en magnetische vectorvelden nodig (de achtvoudige weg, alweer). De ladingen die de quarks hebben zijn een beetje ingewikkelder dan gewone elektrische en magnetische ladingen, waar je alleen maar spreekt van plus en min, die elkaar kunnen neutraliseren. Wie voor het eerst de analogie met ‘kleur’ aanvoerde weet ik niet, maar zij ligt erg voor de hand. Iedere quarksoort (up, down, strange, ...) kan een ‘kleur’ hebben: rood, groen of blauw. Quarks met verschillende kleuren trekken elkaar aan, en vormen dan klonters die een mengkleur hebben. De enige klonters die vrij in de natuur voor kunnen komen zijn echter een zodanig mengsel van quarks dat ze ‘kleurloos’ zijn geworden (wit of een grijstint) volgens de regel rood + groen + blauw = wit. | |
[pagina 125]
| |
De antiquarks hebben de geconjugeerde kleuren: zeegroen, violet of geel. De Yang-Millsfotonen worden gluonen genoemd (‘glue’ = lijm). Zij dragen zowel een kleur als een antikleur. Dat kan op negen manieren, maar één van de combinaties kan kleurloos genoemd worden en doet daarom niet mee, zodat er acht gluonsoorten zijn. Quarks, antiquarks en gluonen tezamen zijn dus Feynmans partonen. En hoe zit het met het Higgs-Kibblemechanisme? In de begintijd dacht men erover de theorie voor de sterke kracht net zo te construeren als die voor de zwakke kracht; de ‘naakte’ gluonen hebben dan geen rustmassa. Maar zulke massaloze vectordeeltjes zijn er niet in de vrije natuur. Dus moesten ze een massa krijgen via het Higgs-Kibbleformalisme. Maar, wacht eens even, deeltjes met massa en de eigenschappen van gluonen (zoals hun kleuren) zijn er óók niet! Het antwoord moest anders zijn. Nu weten we dat er bij de sterke kracht helemaal geen sprake is van een Higgs-Kibblemechanisme. Er is een principe dat ieder deeltje of iedere gebonden toestand van deeltjes waarvan de totale kleur niet volledig is geneutraliseerd, verbiedt. Wanneer men zou proberen uit een kleurloos brouwsel een deeltje of wat dan ook met kleur te isoleren, dan heeft datgene wat achterblijft de geconjugeerde kleur. De aantrekkende kracht tussen kleur en geconjugeerde kleur is zo groot dat de energie die nodig zou zijn om ze te scheiden oneindig is. Zo'n isolatieproces is daarom onmogelijk. In 1973 begrepen we nog niets van de diepere wiskundige achtergrond van dit principe, maar het was niet moeilijk er een naam voor te bedenken: ‘confinement’, ofwel permanente opsluiting. Onze volgende taak was het verschijnsel van de quarkopsluiting te begrijpen en te verklaren. En nu kom ik terug op de wonderbaarlijke formule van Veneziano die ik in het begin van dit hoofdstuk noemde. Op dit gebied had de Deen Holger Nielsen samen met Ziro Koba vorderingen gemaakt. Nielsen, maar ook anderen zoals Nambu, | |
[pagina 126]
| |
hadden ontdekt wat deze formule nu eigenlijk voorstelt. Die formule krijg je namelijk ook als je alle hadronen voorstelt als stukjes touw, met quarks aan hun uiteinden. De touwtjes zijn van een soort supermateriaal gemaakt. Ze zijn altijd heel strak gespannen, zodat het veel energie kost om ze uit te rekken. Als je zo'n touwtje toch weet uit te rekken, wordt de geleverde energie meteen gebruikt om meer touwmassa van te maken. Zo kun je het touw onbeperkt blijven uitrekken. Het wordt steeds langer en de spanning neemt niet af! Als quarks met zulke ideale stukken elastiek aan elkaar verbonden zijn, is het geen wonder dat ze niet van elkaar af kunnen komen. Het ingeburgerde Engelse woord voor het touwtje dat de quarks bij elkaar houdt, is ‘string’, maar mijn uitgever heeft liever dat ik dit netjes in het Nederlands vertaal, en ik zal het dus over ‘snaren’ hebben. Als je de snaar heel ver uitrekt wordt hij langer, maar er kan ook iets anders gebeuren. Hij kan namelijk best knappen, maar niet zonder dat er weer een quark en een antiquark aan de nieuw ontstane uiteinden worden gezet. Uiteinden zonder quarks of antiquarks eraan bestaan dus niet. En altijd als er een quark aan het ene uiteinde zit, zit er een antiquark aan het andere uiteinde. Baryonen, die uit drie quarks bestaan, krijg je door toe te staan dat drie snaaruiteinden op bepaalde wijze aan elkaar kunnen worden geknoopt. De spankracht van een snaar is een natuurconstante: alle quarks worden bijeengehouden door een kracht van ongeveer 14 ton. Ogenschijnlijk lijkt deze snarentheorie niet te rijmen met de theorie die zegt dat quarks bijeengehouden worden door ijkvelden. Maar de Venezianoformule was slechts ongeveer goed, zij is niet exact waar. Het ligt voor de hand te vermoeden dat de omschrijving in termen van touwtjes met quarks aan de uiteinden slechts een benadering is. Wat we nu geloven is dat de veldlijnen van het ijkveld tussen de quarks een patroon vormen zoals geschetst in figuur 14c. Als je probeert de quarks uit elkaar | |
[pagina 127]
| |
te trekken wordt de toegeleverde energie gebruikt om meer veldlijnen tussen de quarks te creëren. Misschien vindt u deze verklaring acceptabel, en de plaatjes van figuur 14 mooi en overtuigend. Maar er is een belangrijk probleem. De berekeningen die ik eerder heb genoemd, zoals het magnetische moment van het elektron, de renormeerbaarheid van de zwakke kracht en het verschijnsel ‘asymptotische vrijheid’, konden met grote precisie worden verricht. Je begint met een volledig stelsel vergelijkingen, waarvan je om een of andere reden gelooft dat ze iets interessants beschrijven (een model dus), en je leidt dan met wiskundige precisie de eigenschappen af die je wilt begrijpen. 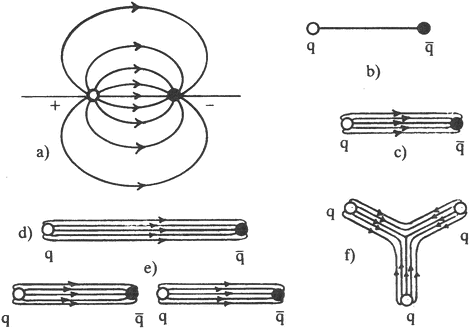
Figuur 14. a) Veldlijnen tussen twee ladingen in de Maxwelltheorie voor elektromagnetisme. b) Snarentheorie. c) Het gluonveld tussen quark en antiquark. d) Bij uitrekken wordt er meer veld gecreëerd, tot er (e) een nieuw quark-antiquarkpaar wordt gecreëerd. f) Het baryon. q = quark, q̄ = antiquark.
| |
[pagina 128]
| |
En zover was het nog helemaal niet met net verschijnsel quarkopsluiting. We konden de vergelijkingen opschrijven: een Yang-Millstheorie met kleurfotonen en fermionen, dat wil zeggen quarks, precies volgens de regels van hoofdstuk 12. We konden laten zien dat die theorie renormeerbaar is en asymptotisch vrij. Dat laatste betekent dat de krachten relatief klein worden voor quarks die heel dicht bij elkaar komen. Omgekeerd, als quarks zich ver van elkaar verwijderen, nemen de krachten minder snel af dan bij een elektromagnetische theorie. Tot zover stond alles onomstotelijk vast. Maar waarom vormen de krachtlijnen snaren? Waarom wordt de energie die nodig zou zijn om de quarks uit elkaar te halen oneindig groot? Bij deeltjes die elkaar elektrisch vasthouden (zoals atomen in moleculen) zou dit de ionisatie-energie zijn. Waarom is dus voor de quarks deze ionisatie-energie oneindig groot? De plaatjes van figuur 14 zijn suggestief, maar zijn ze goed? Volgen ze uit de vergelijkingen waar we in geloven? Helaas, juist omdat de krachten groot worden, worden de berekeningen onbetrouwbaar. Dit is het zogenaamde quarkopsluitingsprobleem. Zoals ik de zaken nu zie, moet je de oplossing van dit probleem in twee gedeeltes splitsen. Ten eerste moet je een algemeen scenario vinden, een nauwkeurige beschrijving van deze merkwaardige eigenschap van de theorie. We hebben hier te maken met een fasetoestand, vergelijkbaar met de vaste, vloeibare of gasvormige toestand van gewone materie, of met supergeleiding of het Higgs-Kibblemechanisme. De confinementfase is een toestand waarin de fotonen niet een massa krijgen en de ladingen afschermen, maar de ladingen oneindig sterk aan elkaar binden. In deze zin zouden we quarkopsluiting later goed gaan begrijpen, en ik kom er nog op terug. De tweede vraag is of deze fasetoestand inderdaad optreedt, en onder welke voorwaarden. Deze vraag is heel wat moeilijker, vergelijkbaar met de vraag welke materialen bij | |
[pagina 129]
| |
zeer lage temperatuur supergeleidend worden en welke niet. Welke materialen zijn vloeibaar en welke vast, en bij welke temperatuur? Dat moet volgen uit de basiskrachten tussen de atomen of elementaire deeltjes onderling. Het antwoord hangt van zeer technisch ingewikkelde en uitgebreide berekeningen af, meestal gedaan met grote computers. Met pen en papier gaat het niet meer, omdat de krachten tussen de deeltjes zo groot zijn dat geen enkele eenvoudige benaderingsmethode betrouwbaar meer is. Zelfs de berekeningen die men nu (2002) doet met de allergrootste computers geven uitkomsten die nog helemaal niet zo erg nauwkeurig zijn, maar alles wijst erop dat quarkopsluiting inderdaad optreedt in een kleurijktheorie.1 Rond 1974 begon het idee van een pure kleurijktheorie voor de sterke kracht, zonder spin-0-deeltje en zonder Higgs-Kibblemechanisme, steeds meer aanhang te krijgen. De theorie werd quantumchromodynamica genoemd, naar het Griekse χϱῶμα = kleur. Deze theorie drong eigenlijk langzaam maar zeker tot de onderzoekers door. Niet één naam, maar vele zijn eraan verbonden. Heel anders dan het ontstaan van de relativiteitstheorie en de quantummechanica, maar niet minder revolutionair! Want wat is er allemaal door veranderd! Slechts één fundamentele natuurconstante was nog onbepaald in de fundamentele vergelijkingen van de theorie. Daarna hoefde je alleen nog maar de massa's van de quarks aan te geven, en alleen als deze veilig bij elkaar zitten zijn de massaparameters van enige betekenis; verder zijn ze onbelangrijk. Dat betekende dus dat je alle eigenschappen van de hadronen zou moeten kunnen uitrekenen! Nog maar enige jaren terug had niemand van de aanwezigen in onze zomerschool in Cargèse zo'n theorie voor mogelijk gehouden. Dat de theorie maar langzaam populair werd was wel te begrijpen. Want al waren de berekeningen in principe mogelijk, het zou nog jaren duren voordat de grote computers resultaten | |
[pagina 130]
| |
te zien gaven die ergens op leken.Ga naar voetnoot1 Wel werden er voorspellingen gedaan. De sterke kracht zou, op heel kleine schaal gezien, zich als een zwakke kracht manifesteren. Maar hoe kun je dat in een experimentele opstelling controleren? Ik ga nu even vooruitlopen op mijn verhaal. Als je deeltjes tegen elkaar aanschiet met energieën die veel groter zijn dan de massa's van de gewone kerndeeltjes (de hadronen), gedragen deze hadronen zich als een soort sponzige sneeuwballen waar de quarks als kleine harde pitjes in rondwentelen. Bij de meeste botsingen schieten die quarks gewoon langs elkaar heen en stuift de sneeuw uiteen. De doorgaande quarks bevatten de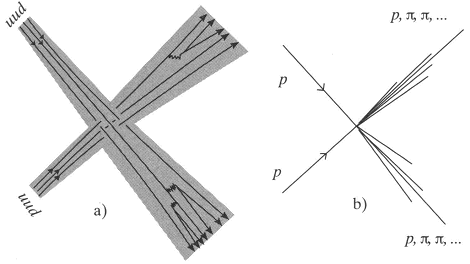
Figuur 15. a) Twee protonen botsen tegen elkaar zonder dat de quarks elkaar direct treffen (een ‘perifere’ botsing). b) Wat de experimentator ziet.
| |
[pagina 131]
| |
meeste energie. Dit zijn de minder interessante botsingen (figuur 15). 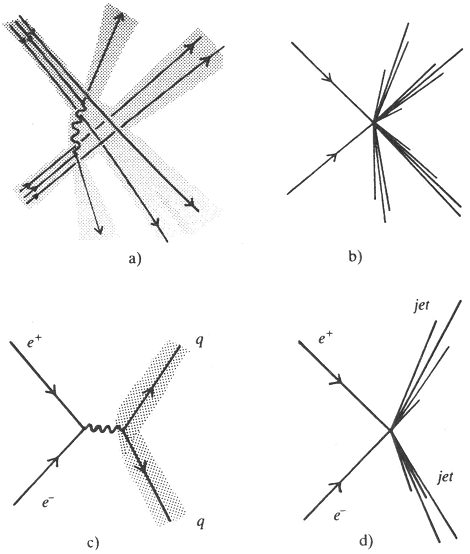
Figuur 16. a) Twee quarks raken elkaar. b) Wat de experimentator dan ziet: een typische ‘jet’. c) e+ + e- → 2 quarks. d) Zoals deze gebeurtenis er in het experiment uitziet.
| |
[pagina 132]
| |
Zo nu en dan echter botsen twee quarks tegen elkaar op. Deze vervolgen hun weg zijwaarts, waarbij ze andere quarks en gluonen meeslepen teneinde hun kleurlading te compenseren. Er ontstaan dan twee (of soms zelfs meer) compacte wolkjes hadronische deeltjes die de baan van de oorspronkelijke quarks blijven volgen. We noemen deze wolkjes jets. Wat de experimentator ziet is geschetst in figuur 16. Ook in andere experimenten manifesteren de quarks en gluonen zich als ‘jets’. Bijvoorbeeld, als je een elektron tegen een positron aanschiet kunnen deze elkaar annihileren onder uitzending van een foton, dat dan weer een quark-antiquarkpaar produceert (figuur 16c). Deze geproduceerde quarks vormen dan weer wolkjes hadronen: een tweetal jets (figuur 16d). Er kan dan ook een derde of nog meer deeltjes geproduceerd worden, meestal gluonen. Ook deze manifesteren zich als jets. Kortom, de oorspronkelijke quarks en gluonen die bij een botsingsproces ontstonden verraden hun aanwezigheid vermomd als jets. Door deze jets nu zorgvuldig te meten, kunnen we de theorie direct toetsen. In het bijzonder zijn we nu in staat de interactiesterkte tussen quarks en gluonen te meten. Iedere keer als er een nieuwe deeltjesversneller in gebruik werd genomen, bestreek deze weer een hoger energiegebied, en zo werden wij in staat gesteld de interactiesterkte tussen quarks te meten bij toenemende energie. We zien deze steeds verder afnemen, geheel in overeenstemming met ‘asymptotische vrijheid’. |
|

