De bouwstenen van de schepping

Een zoektocht naar het allerkleinste

[p. 97]

11 De supergeleidende lege ruimte: het Higgs-Kibblemechanisme

Een uitweg uit de moeilijkheden was er wel. Deze vindt zijn oorsprong in een heel andere tak van de theoretische natuurkunde, namelijk de fysica van metalen bij zeer lage temperatuur. Bij zeer lage temperatuur kunnen ‘quantumverschijnselen’ ineens heel opmerkelijke effecten teweegbrengen. Om die effecten te beschrijven gebruikt men gequantiseerde veldentheorieën, precies als in de elementaire deeltjesfysica. De natuurkunde van elementaire deeltjes heeft niets met lage temperaturen te maken, maar hun wiskunde lijkt er heel veel op!

Het ‘veld’ dat in een of ander materiaal bij zeer lage temperatuur belangrijk wordt, kan het veld zijn dat de uitwijkingen van de atoomkernen uit hun evenwichtsstand beschrijft, of het veld dat de elektronen in dat materiaal beschrijft. Bij zeer lage temperatuur krijgen we te maken met de quanta van deze velden. Zo is het fonon het quantum van geluid. Zijn gedragingen lijken veel op die van het foton, het quantum van licht, maar alleen de bijbehorende getallen zijn heel verschillend: fononen gaan met de geluidssnelheid, ongeveer 300 meter/sec; het foton daarentegen heeft de lichtsnelheid, 300.000 kilometer/sec! De elementaire deeltjes die ons interesseren komen meestal heel dicht bij deze laatste snelheid.

Een van de meest bijzondere ‘quantum’-verschijnselen die zich kunnen voordoen in sterk gekoelde metalen is de zogenaamde supergeleiding. De weerstand die het materiaal biedt tegen elektrische stroom wordt exact nul. Een gevolg daarvan is dat het materiaal geen enkel elektrisch spanningsverschil duldt, want dat zou ogenblikkelijk door een ‘ideaal’ stroompje geneutraliseerd worden. Bovendien blijkt dat ook magnetische velden in principe niet binnen een supergeleider kunnen doordringen omdat volgens de vergelijkingen van Maxwell het

[p. 98]

aanschakelen van zo'n magnetisch veld gepaard zou gaan met inductiestroompjes. Zolang er geen weerstand tegen deze stroompjes wordt geboden, neutraliseren deze ieder magnetisch veld volledig. Er kan dan geen enkel elektrisch of magnetisch veld binnendringen in een supergeleider. Deze situatie wordt alleen anders als de geïnduceerde stroompjes te sterk worden, want dan verstoren deze de supergeleider. Dat gebeurt als men aan komt zetten met heel sterke magneten; tegen bruut geweld zijn supergeleiders niet opgewassen. Ze verliezen dan hun supergeleidend vermogen en laten dan het veld gewoon toe.

Waarom breng ik nu ineens de supergeleider te berde? Welnu, men kan dit materiaal opvatten als een systeem waarin het elektromagnetische veld een veld met zeer kleine reikwijdte is. Het wordt afgeschermd. En toch is het Maxwellveld een ijkveld. Dit maakt de supergeleider zeer interessant voor wie de zwakke kracht tussen de elementaire deeltjes wil beschrijven! Dit is nu het aardige van de theoretische natuurkunde: je kunt vaak totaal verschillende werelden met elkaar vergelijken omdat ze toevallig aan dezelfde wiskundige vergelijkingen gehoorzamen.

Hoe werkt de supergeleider? De ware oorzaak van het verschijnsel supergeleiding werd ontrafeld door John Bardeen, Leon N. Cooper en John R. Schrieffer (die hier in 1972 de Nobelprijs voor ontvingen). Er zijn twee bijzondere verschijnselen die zich kunnen voordoen bij de elektronen in een stof en die gezamenlijk tot supergeleiding aanleiding kunnen geven. Het eerste is paarvorming, en het andere is Bose-Einsteincondensatie.

‘Paarvorming’ houdt in dat de elektronen paarsgewijs gaan optreden. De fononen veroorzaken een kracht die de paren bijeen houdt. Twee elektronen in een paar draaien, ieder om hun eigen as, in tegenovergestelde richting, zodanig dat het paar (dat ‘Cooperpaar’ wordt genoemd) als geheel geen draaibeweging meer vertoont. Een Cooperpaar gedraagt zich als een

[p. 99]

deeltje¹ met spin 0 en elektrische lading - 2.

‘Bose-Einsteincondensatie’ is een typisch quantummechanisch verschijnsel. Het kan zich alleen voordoen bij deeltjes met heeltallige spin (bosonen). Als lemmingen kunnen deze zich met z'n allen in de allerlaagste energietoestand storten die mogelijk is. U herinnert zich: bosonen doen graag allemaal hetzelfde. In deze toestand nu kunnen ze zich nog wel verplaatsen maar er kan geen energie meer aan onttrokken worden. Het gevolg is dat de verplaatsing zonder enige weerstand gebeurt. De Cooperparen verplaatsen zich dus vrijelijk, zodat er elektrische stromen kunnen zijn. Deze stromen ondervinden geen enkele weerstand meer. Een soortgelijk verschijnsel doet zich voor in vloeibaar helium bij zeer lage temperatuur. Het zijn dan de heliumkernen zelf die Bose-Einsteincondenseren. Het gevolg is dat deze vloeistof kan stromen door de allerkleinste gaatjes zonder enige weerstand.²

Omdat afzonderlijke elektronen spin ½ hebben, kunnen deze zelf geen Bose-Einsteincondensatie ondergaan. Deeltjes met halftallige spin (fermionen) moeten altijd alle in een verschillende quantumtoestand zitten, vanwege Pauli's uitsluitingsprincipe. Vandaar dat supergeleiding pas kan optreden als er paarvorming heeft plaatsgehad. Ik heb hier weer formules vertaald in woorden; vindt u die ‘quantumlogica’ niet heerlijk?

Dat supergeleiding ook voor elementaire deeltjes van belang

1 Merkwaardigerwijs zitten de elektronen maar heel losjes in zo'n paar. De situatie lijkt een beetje op een dansvloer waar heel wilde popmuziek wordt gedraaid: het is bij de dansparen nauwelijks meer te zien wie bij wie hoort. Schrieffer legde later uit waarom zijn theorie zo moeilijk was: het is de choreografie van een dans voor meer dan een miljoen maal een miljoen maal een miljoen dansparen.

2 Maar er geldt wel een beperking voor de stroomsnelheid, die onder een kritische grens moet blijven. Alleen zolang de snelheid daaronder blijft, wordt er dus geen weerstand geboden.

[p. 100]

kan zijn, werd ontdekt door de Belg François Englert, de Amerikaan Robert Brout en de Schot Peter Higgs. Zij stelden een model van elementaire deeltjes voor waarin elektrisch geladen deeltjes zonder spin Bose-Einsteincondensatie ondergaan. Deze keer echter vindt de condensatie niet plaats binnen een of andere substantie, maar in de lege ruimte (vacuüm). De krachten tussen deze deeltjes zijn dan zodanig gekozen dat het energetisch gunstiger is de ruimte te vullen met deze deeltjes dan haar strikt leeg te houden. Die deeltjes zijn dan niet direct waarneembaar. Wij zouden die toestand, waarbij de ruimte krioelt van de Higgsdeeltjes (zoals ze nu worden genoemd) maar waarbij de energie de laagst mogelijke waarde aanneemt, aanzien voor een lege ruimte.

De Higgsdeeltjes zijn de quanta van het ‘Higgsveld’. Het kenmerkende van een Higgsveld is dat de energie die erin opgeborgen is, het kleinst is wanneer dit veld een bepaalde sterkte heeft, en niet wanneer het nul is. Wat wij als ‘lege ruimte’ ervaren is niets anders dan die deeltjesconfiguratie die de laagst mogelijke energie heeft. Dit is de reden waarom in de ‘lege ruimte’ het Higgsveld een karakteristieke sterkte heeft. Als we overgaan van veldjargon naar deeltjesjargon betekent dit dat die zogenaamde lege ruimte in feite vol zit met Higgsdeeltjes. Zij zijn ‘Bose-Einstein-gecondenseerd’.

Deze lege ruimte heeft nu alle eigenschappen die ook vertoond worden in het inwendige van een supergeleider. Het elektromagnetische veld heeft er een zeer korte reikwijdte. Dit hangt dan direct samen met het feit dat het foton in deze wereld een zekere rustmassa heeft. Toch kan men in zo'n model ook aangeven hoe een ijktransformatie uitgevoerd moet worden; de velden die door de Higgsdeeltjes worden gegenereerd veranderen dan echter ook, en dat maakt de transformatie ingewikkelder. Het is vanwege de ingewikkelde, niet-symmetrische structuur van de lege ruimte zelf, dat in dit model de ijkdeeltjes massa kunnen hebben. Men noemt dit wel ‘spontane symmetriebreking’.

[p. 101]

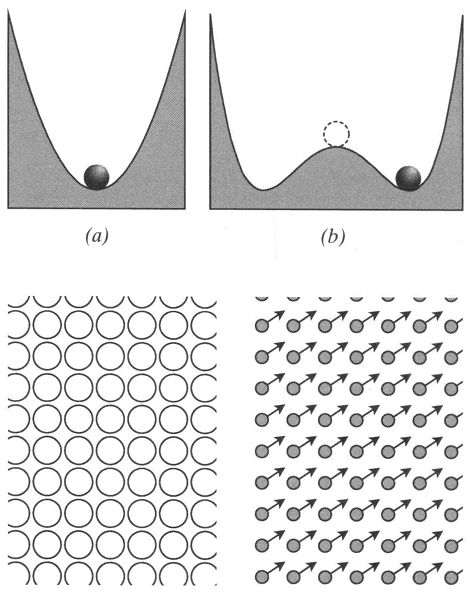
Figuur 10. Symmetrie en spontane symmetriebreking. Een systeem dat aan een symmetrische vergelijking voldoet, kan dan ook een symmetrische oplossing hebben (a), maar het kan ook zijn dat een minder symmetrische oplossing stabieler is (b). Ook een veld, dat een bepaalde richting kan hebben, kan een symmetrische waarde aannemen (c), of het kan zijn dat de meest stabiele oplossing van de vergelijkingen niet symmetrisch is (c). In zo'n wereld lijken alle natuurverschijnselen de oorspronkelijke symmetrie van de vergelijkingen te hebben verloren.

[p. 102]

Nu had Higgs het nog over ‘gewone’ elektromagnetische velden. Thomas Kibble vond uit dat je ook een Yang-Millstheorie supergeleidend kunt maken, door er een spinloos deeltje met Yang-Millslading aan toe te voegen, dat dan Bose-Einsteincondensatie kan ondergaan. De Yang-Millskrachten krijgen dan ook een korte reikwijdte, en de Yang-Millsfotonen worden spin-1-deeltjes met massa.

Was dit dan niet precies de oplossing van het probleem waarover het vorige hoofdstuk ging? De Yang-Millsfotonen krijgen hun massa en het ijkprincipe blijft overeind! Ik geloof dat er twee redenen waren waarom deze benadering niet onmiddellijk de aandacht kreeg die zij verdiende.

Ten eerste vond men de theorie lelijk. Het ijkprincipe was er nog wel maar stond niet meer centraal. Het Higgsveld was er ‘met de hand bijgestopt’ en het Higgsdeeltje zelf is niet een ‘ijkdeeltje’. Als je daaraan begint, waarom dan nog niet veel meer willekeurige deeltjes en velden erbij? Men beschouwde deze ideeën als eenvoudige speelgoedmodellen zonder veel fundamentele betekenis.

Ten tweede was er het ‘Goldstonetheorema’. Deeltjesmodellen met een ‘spontane symmetriebreking’ waren al eerder voorgesteld, maar van een uitgebreide klasse van zulke modellen had Jeffrey Goldstone bewezen dat ze altijd massaloze deeltjes zonder spin bevatten. Vele onderzoekers dachten dat daarom ook de Higgstheorie zo'n massaloos Goldstonedeeltje moest bevatten, wat vervelend zou zijn want er bestaan voorzover we weten geen echte Goldstonedeeltjes.¹ Goldstone kon nu wel zeggen dat het Higgsmodel niet aan de voorwaarden voor zijn bewijs voldeed, zodat zijn bewijs daar niet geldig voor was, maar men liet zich zo imponeren door die mooie wiskunde dat het Higgs-Kibblemodel langere tijd weinig populair was.

Goldstone's stelling werd dus gebruikt als een ‘gaat-niet-stel-

1 Er bestaan wel bijna-Goldstonedeeltjes, zie het volgende hoofdstuk!

[p. 103]

ling’: als de lege ruimte niet symmetrisch is, kan dat niet anders dan met massaloze, spinloze deeltjes erin. Nu weten we dat vanwege de kleine lettertjes de stelling in dit geval buiten werking wordt gesteld; de Goldstonedeeltjes worden precies vanwege de ijkinvariantie onzichtbaar: het zijn slechts de ‘spookdeeltjes’ die Feynman voor het eerst tegenkwam in zijn berekeningen.

Dat je wel degelijk realistische deeltjesmodellen kunt fabriceren waarin een Yang-Millsveldensysteem verantwoordelijk is voor de zwakke kracht, en het Higgs-Kibblemechanisme voor de korte reikwijdte daarvan, was niettemin wel gesuggereerd door twee prominente onderzoekers. Eén daarvan was de Pakistani Abdus Salam. Salam zocht naar esthetische modellen voor deeltjes, en hij vond het Yang-Mills-idee zo mooi dat alleen daarom al geprobeerd moest worden dit in te bouwen in de zwakke-interactietheorie. De drager van de zwakke kracht moest dus een Yang-Millsfoton zijn, en het Higgs-Kibblemechanisme is de enige aanvaardbare verklaring voor het feit dat die drager een eindige rustmassa heeft.

In een vergadering die werd gesponsord door het Zweedse Nobelconsortium legde Salam de ideeën die hij samen met zijn medeauteur John Ward had uitgebroed, voor. Zijn lezing, en de discussie die volgde, werd gepubliceerd, en de vraag die daarin weldra centraal kwam te staan, was of de theorie wel renormeerbaar was. Intuïtief begreep Salam dat het antwoord bevestigend moest zijn, maar de details moest hij de vragenstellers schuldig blijven. Hij was niet in staat de Feynmanregels te formuleren en hij moest erkennen dat de theorie, als je haar neemt zoals ze eruitziet, spookdeeltjes voorspelt die de boel verzieken: negatieve energieën, en/of negatieve productiekansen, beide onaanvaardbaar als je zo'n theorie sluitend wilt maken.

De andere onderzoeker die op ongeveer hetzelfde punt uitkwam was Steven Weinberg. Weinberg echter ging nog een belangrijke stap verder. Hij formuleerde in detail een eenvoudig model waarin hij precies aangaf welke velden er zijn en hoe

[p. 104]

deze wisselwerken, waarbij hij zich echter tot de leptonen beperkte. Weinberg realiseerde zich dat er naast het gewone foton minstens drie soorten zware Yang-Millsfotonen moesten zijn: één positief, één negatief en één neutraal foton. Over de geladen fotonen was iedereen het wel eens; dat werden dan de befaamde intermediaire vectorbosonen, met een massa die volgens Weinbergs theorie meer dan 60.000 MeV moest zijn. Maar met die geladen vectorbosonen kun je praktisch alle zwakke interactieprocessen verklaren. Dat er dan ook naast het gewone foton (γ) nóg een neutrale component (die Weinberg Z^o noemde) nodig zou zijn, was lang niet zo vanzelfsprekend. De massa van Z^o zou nog iets meer dan die van de geladen bosonen moeten zijn. Figuur 11 geeft aan hoe men zich voorstelt dat de zwakke interacties plaatsvinden. Het was echter bekend dat ‘neutrale’ uitwisselingsprocessen nooit werden waargenomen. Het diagram c is om een of andere reden verboden!

Dit is een moeilijkheid als men in een neutraal Z^o-deeltje wil geloven. Nog opvallender wordt het wanneer men de levensduur van het π^- vergelijkt met die van K_lang. Waarom vervalt π^- wel in μ^- en ν_μ, terwijl K_lang gedurende zijn langere levensduur nooit via een Z^o bijvoorbeeld in μ⁺ en μ^- vervalt? Weinberg zag echter dat de strenge wiskunde van het Yang-Mills-systeem wel degelijk het bestaan van een stroomcomponent voor een neutraal Z^o-deeltje vereiste. Hij veronderstelde nu dat er kennelijk nog iets niet helemaal klopte met de hadronen. Vandaar dat zijn publicatie als titel had: Een model voor leptonen. Voor de leptonen is de belangrijkste nieuwe consequentie van het neutrale Z^o-deeltje dat het botsingsproces ν_μ + e^- → ν_μ + e^- mogelijk werd (figuur 12).

Weinberg stelde dat zijn theorie door het experiment kon worden getoetst. Weliswaar waren er al neutrino-experimenten gedaan maar het bestaan van interacties zoals deze was nog onzeker. Overigens zou ook de mate waarin elektronneutrino's tegen elektronen botsen door de Z^o-deeltjes beïnvloed worden.

[p. 105]

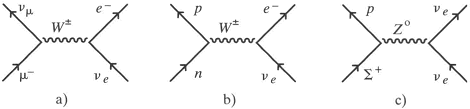
Figuur 11. Diagrammen die laten zien hoe een zwakke interactie kan ontstaan door uitwisseling van een intermediair vectorboson W^-. Het diagram a geeft aan dat μ^- + ν_e → ν_μ + e^- hetzij via de tussentoestand ν_μ + W^- + ν_e, hetzij via μ^- + e^- + W⁺. Volgt men de pijltjes andersom dan zien we de interacties voor de desbetreffende antideeltjes. Het diagram geeft dan aan hoe μ^- vervallen kan in ν_μ + e^- + ν̄_e (het antineutrino). Diagram b geeft aan hoe n → p + e^- + ν̄_e. Diagram c geeft aan hoe een neutrale drager het Σ⁺ zou kunnen doen uiteenvallen. Het weergegeven vervalproces doet zich echter niet voor!

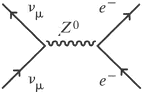
Figuur 12. Muonische neutrino's kunnen alleen (elastisch) tegen een elektron botsen als er een neutraal Z^o-deeltje wordt uitgewisseld.

Ook Weinberg veronderstelde dat zijn model renormeerbaar zou zijn maar kon de wiskundige voorschriften niet formuleren. Dat was in 1967. Rond 1970 hadden zowel Weinberg als Salam hun belangstelling voor de Yang-Millstheorie verloren. Er kwamen theorieën voor de zwakke interactie waarbij andere diagrammen dan die van figuur 11 de hoofdrol gingen spelen; theorieën waarin je oneindig veel diagrammen had, en theorieën volgens welke negatieve kansen of een lichte schending

[p. 106]

van causaliteit toegestaan zouden kunnen zijn. Nu, achteraf, is het gemakkelijk te zeggen waarom zulke ideeën gedoemd zijn tot falen, maar in die tijd moest men alle mogelijkheden en onmogelijkheden onderzoeken.

Werk genoeg dus voor de jonge onderzoeker. In vergelijking met anderen las ik weinig en ik dacht veel na. Dat houdt het risico in dat je er soms heel lang over doet iets te ontdekken wat achteraf al lang bekend blijkt te zijn, maar het gevolg is wel dat je de problematiek veel beter gaat begrijpen. Zo verging het mij ook bij het Higgs-Kibblemechanisme (ik geloof niet dat ik toen al wist dat het zo heette). Veltman stond heel sceptisch tegenover deze ideeën; hij was er niet van te overtuigen dat wat wij lege ruimte noemen misschien wel tot de nok gevuld is met onzichtbare deeltjes. Hij zou heel lang blijven volhouden dat hij dit onaannemelijk vond, en hij ging zelfs zwaaien met de stok die die theorie tot moes zou moeten slaan. Want zouden al deze deeltjes in de lege ruimte hun aanwezigheid niet verraden door hun zwaartekrachtsveld? Je kunt de theorie zo opstellen dat dat zwaartekrachtsveld precies gecompenseerd wordt door andere onzichtbare deeltjes of door een geheimzinnige bijdrage van de lege ruimte zelf. Hoe de natuur het klaarspeelt de zwaartekrachtseffecten van de onzichtbare vacuümdeeltjes zo volledig te maskeren dat wij er helemaal niets van merken, is nog steeds een raadsel dat volop in de belangstelling staat. Wat mij betreft echter moet dit probleem worden uitgesteld tot we de theorie van de zwaartekracht zelf beter begrijpen.