De bouwstenen van de schepping
(1992)–Gerard 't Hooft–Een zoektocht naar het allerkleinste
[pagina 86]
| |
10 De Yang-MillstheorieWe gaan terug naar 1954. De grote successen van de theorie voor de elektromagnetische krachten tussen de deeltjes waren nog vers. Nog niet ontmoedigd door de ontdekkingen van vele soorten deeltjes die nog in het verschiet lagen, zocht men nog naar eenvoudige, elegante en universele principes in de natuurkunde. Alle aspecten van de elektromagnetische krachten die tussen de deeltjes heersen, kunnen worden afgeleid uit de vergelijkingen waaraan het elektrische en het magnetische veld voldoen. Deze velden zijn vectorvelden. Een ‘vector’ is een grootheid die niet alleen een sterkte heeft maar ook een richting. De windsterkte in de atmosfeer zou je een vectorveld kunnen noemen. Zo'n vector heeft drie componenten. Van de wind bijvoorbeeld kun je eerst aangeven in welke mate de lucht van zuid naar noord beweegt (of andersom, dan zet je er een minteken voor), dan ten tweede de oost-westbeweging en ten slotte de verticale component. Bij elkaar heeft het elektromagnetische veld dus zes componenten, maar deze kun je niet alle willekeurig kiezen; ze hangen via ‘veldvergelijkingen’ met elkaar samen, zoals ook de windsnelheid weer samenhangt met de drukverdeling in de atmosfeer. Als je de drukverdeling kent dan volgt daar de windsnelheid uit. Zoiets is er ook bij het elektromagnetische veld. Je kunt het elektrische spanningsveld invoeren dat net als luchtdruk door slechts één getal, niet drie, wordt aangegeven. Voorts heb je nog een vectorspanningsveld nodig. Tezamen hebben we dus vier spanningsveldcomponenten, die ik gemakshalve bij elkaar neem en die ik ‘vectorpotentiaal’ zal noemen. Als je de volledige vectorpotentiaal kent, weet je ook wat het elektrische en het magnetische veld zijn. Er is echter iets bijzonders aan de hand met de vectorpoten- | |
[pagina 87]
| |
tiaal. Hij is niet direct waarneembaar. Preciezer gezegd: je kunt een heleboel verschillende vectorpotentiaalvelden verzinnen die alle hetzelfde elektromagnetische veld genereren en daarom experimenteel ononderscheidbaar worden, bijvoorbeeld, de aarde zou op een spanning van 100.000 volt kunnen staan: uit de twee gaatjes in mijn stopcontact zou dan respectievelijk 100.000 en 100.220 volt kunnen komen, het strijkijzer werkt als vanouds en ik word er niet door geëlektrocuteerd. U zou kunnen opperen dat door die willekeur het vectorpotentiaalveld onbruikbaar is, maar het tegendeel is waar. De bewegingsvergelijkingen voor de elementaire deeltjes worden er een heel stuk eenvoudiger en eleganter door. Je moet de willekeur in de beschrijving, die we ijkinvariantie noemen, voor lief nemen. In de praktijk is ijkinvariantie zelfs heel prettig. Als je een ingewikkelde berekening hebt gedaan en je ervan wilt verzekeren dat er niet ergens onderweg een foutje is gemaakt, hebben we nu een mooie controlemogelijkheid. We veranderen de vectorpotentiaal op zo'n onzichtbare manier. We noemen dat een ijktransformatie. Het eindresultaat (welke deeltjes werden er geproduceerd, hoeveel en in welke richting?) mag dan niet veranderen. Of het zou kunnen zijn dat er deeltjes ontstaan die we een andere naam hadden gegeven, maar door de experimentator niet van de vorige te onderscheiden zijn. Om het voorbeeld van het strijkijzer weer even aan te halen: als ik uitreken hoe warm het strijkijzer wordt, mag het rekenresultaat niet veranderen als ik aan beide gaatjes van mijn stopcontact 100.000 volt toevoeg. Dit alles heet dus ijkinvariantie. IJkinvariantie loopt als een rode draad door de gehele theorie van de quantumelektrodynamica. Een soortgelijk principe hebben we ook in Einsteins theorie voor de zwaartekracht. Daar zijn het de coördinaten van de punten in ruimte en tijd die willekeurig mogen worden gekozen. Door experimentatoren waargenomen verschijnselen mogen niet afhangen van onze coördinatenkeuze. | |
[pagina 88]
| |
Als ijkinvariantie zo'n belangrijk principe is in de enige twee krachtsystemen die men in 1954 goed kende dan lag het voor de hand om ook te proberen ‘ijktheorieën’ te construeren voor andere natuurkrachten. Dit was precies het uitgangspunt van een zeer elegante berekening die Chen Ning Yang samen met zijn jongere medewerker Robert Mills toen publiceerde. Achteraf bleek dat ook anderen dit idee hebben gehad. Met name Ronald Shaw, een student van Abdus Salam in Cambridge, had zijn dissertatie zo goed als voltooid toen het artikel van Yang en Mills uitkwam. De resultaten die hij in een hoofdstuk van zijn dissertatie beschreef, waren dezelfde, maar werden niet meer gepubliceerd. Kennelijk heeft Shaw geaccepteerd dat iemand hem vóór was. Wetenschappers van onze tijd kunnen vaak veel slechter tegen hun verlies; die proberen in zo'n omstandigheid tóch hun werk gepubliceerd te krijgen, om vervolgens met veel tamtam te verkondigen dat zij de ontdekking ‘onafhankelijk’ hebben gedaan. Net als voetbal wordt ook het bedrijven van wetenschap tegenwoordig agressiever gespeeld. Het voorstel van Yang en Mills was de groep van toegestane ijktransformaties uit te breiden. Dat kan als je het aantal vectorpotentiaalvelden uitbreidt. De eerste interessante mogelijkheid die zich voordoet, is het geval dat je in plaats van vier nu twaalf componenten invoert. In zo'n wereld heb je drie soorten ‘elektrische’ en drie soorten ‘magnetische’ velden, de Yang-Millsvelden. Voor wat Yang en Mills voorstelden waren eigenlijk maar weinig steekhoudende argumenten aan te voeren. Hun werk moest niet gezien worden als een poging gedragingen van deeltjes te verklaren die men geobserveerd had. Waar hun berekening betrekking op had, zou je moeten opvatten als een ‘droomwereld’, met een niet bestaande eenvoud en abstractie. Dit is een soort exercitie die steeds gewoner wordt in de theoretische natuurkunde, en die bedoeld is om onze wiskundige technieken | |
[pagina 89]
| |
te oefenen en aan te scherpen. We moeten dan spreken van een ‘model’. Daartegenover zou je het woord ‘theorie’ pas mogen hanteren als het model een (eventueel geïdealiseerde) beschrijving is van de werkelijkheid. In de praktijk wordt het helaas steeds meer de gewoonte om de begrippen ‘model’ en ‘theorie’ door elkaar heen te gebruiken. Zou het Yang-Millssysteem op de werkelijke wereld van toepassing kunnen zijn? Het bleek dat in de droomwereld van Yang en Mills drie soorten fotonen bestaan. Eén daarvan is net als het gewone foton en de twee andere zijn elektrisch geladen, één positief en één negatief. Maar eigenlijk zijn ze alle drie gelijk: door ijktransformaties gaan ze in elkaar over. Dus de vraag is: bestaan er in de werkelijke wereld elektrisch geladen deeltjes die we hiermee kunnen identificeren? Nee, zo moesten Yang en Mills tot hun spijt erkennen. Deze elektrisch geladen fotonen zouden spin één hebben, net als het gewone foton, maar rustmassa nul. Dat laatste doet de theorie de das om. Elektrisch geladen deeltjes die heel licht zijn, of zelfs helemaal geen rustmassa hebben, zouden in grote hoeveelheden uit uw stopcontact moeten komen. Omdat het zo weinig energie zou kosten om zulke deeltjes te produceren zouden ze spontaan ontstaan en proberen ieder elektrisch spanningsverschil te neutraliseren. Elektrisch geladen deeltjes met spin één bestaan wel, maar ze hebben massa. Het bekendste voorbeeld is de rho-resonantie (ϱ) met een massa van 770 MeV. Dat deeltje was in 1954 nog niet bekend, maar men had wel vermoedens dat zoiets kon bestaan. Er zijn zowel elektrisch geladen ϱ+ en ϱ- resonanties als een neutrale variant, ϱo. Kon de theorie misschien gewijzigd worden door termen aan de vergelijkingen toe te voegen zodanig dat de massa van de Yang-Millsfotonen niet nul is maar bijvoorbeeld 770 MeV? Dat probeerden Yang en Mills wel, maar ze zagen in dat dan de ijkinvariantie verloren gaat. Dat is lelijk en bovendien was het maar de vraag of zo'n gemutileerde theo- | |
[pagina 90]
| |
rie geen ongerijmdheden bevat. Kortom, de Yang-Millstheorie was aardig maar werd weldra als onrealistisch terzijde gelegd. Toch bleef het artikel van Yang en Mills niet onopgemerkt. Diverse onderzoekers putten inspiratie uit dit fundamentele idee, dat zulke schitterende vergelijkingen opleverde waarvan men alleen niet wist waarop ze nu eigenlijk betrekking hadden. Zo was Gell-Mann duidelijk door deze theorie geïnspireerd toen hij de quarkhypothese opstelde, en ook de Feynman-Gell-Mannformule voor de zwakke kracht leek sterk te wijzen op een of ander Yang-Millsprincipe. Dit is waarover Veltman discussieerde met Bell in Genève. Hoe komt het dat de zwakke kracht zo universeel dezelfde is voor alle soorten deeltjes? Is het niet toevallig dat ook de elektrische lading van de meeste geladen deeltjes exact dezelfde grootte heeft? (Slechts enkele hebben precies tweemaal die hoeveelheid lading). Met een Yang-Millsconstructie zou je dit alles veel beter kunnen gaan begrijpen. De Yang-Millstheorie was immers een directe uitbreiding van de theorie van het elektromagnetisme. De zwakke kracht werkt op een lading die aan een behoudswet lijkt te gehoorzamen. Dat lijkt op wat we bij elektromagnetisme ook hebben. Omgekeerd, elektrische lading komt alleen voor in gehele veelvouden van één fundamentele lading, die van het elektron. Dat nu is typisch een eigenschap die kenmerkend is voor een Yang-Millstheorie. Het lijkt evident dat je het ijkprincipe tot de zwakke kracht moet uitbreiden. Een ander probleem was inmiddels ook door een fysicus op het cern opgelost. De zwakke kracht voor de hadronen bleek namelijk steeds een paar procent zwakker te zijn dan die voor de leptonen. Is die kracht dan bijna maar niet helemaal universeel? Nicola Cabibbo vond de oorzaak.Ga naar voetnoot1 Hij rekende voor dat | |
[pagina 91]
| |
de gewone hadronen de zwakke kracht moeten delen met de vreemde hadronen. De kracht op de hadronen staat als het ware een beetje scheef, waardoor hadronen met vreemdheid door toedoen van de zwakke kracht in gewone deeltjes uiteen kunnen vallen, terwijl deeltjes zonder vreemdheid een iets kleinere kracht voelen. Veltman besloot dat althans iets van die Yang-Millstheorie goed moest zijn. Als je die twee geladen fotonen nou maar een massa kon geven. Een algemeen geldend principe is: als je een krachtvoerend deeltje zoals een foton een zekere hoeveelheid rustmassa geeft dan wordt de kracht die het deeltje overbrengt er een van korte reikwijdte. Volgens de toenmalige theorie van Feynman en Gell-Mann voor de zwakke kracht genereert een zwakke stroom terstond en op dezelfde plek een klein ander stroompje. Alsof er een kracht is met uiterst korte reikwijdte. Algemeen bekend was dat een zeer zwaar krachtvoerend foton hetzelfde effect teweeg zou kunnen brengen. Dat was de theorie van het ‘intermediaire vectorboson’ van de zwakke kracht, die als een schim in onze gedachten rondwaarde. Het zou een heel zwaar, elektrisch geladen deeltje moeten zijn met spin één, het W+ en zijn antideeltje W-. Ieder zwak interactieproces kun je dan zien als het resultaat van twee interacties. Eerst gaat een deeltje over in een soortgenoot (bijvoorbeeld een neutron gaat over in een proton) waarbij er een W-deeltje vrijkomt. Dit W-deeltje heeft een veel te grote rustmassa om vrij te kunnen voortbestaan. De energie hiervoor was niet beschikbaar. Het kan echter wel een tweede interactie aangaan, hetzij door een soortgelijke overgang van een ander deeltje ter plaatse, of door uiteen te vallen in een deeltje en een antideeltje, bijvoorbeeld een elektron en een antineutrino (v̄e), zie figuur 11b. Wat gebeurt er nu precies als je aan de vergelijkingen van Yang en Mills een minimale verandering aanbrengt, juist genoeg om de geladen fotonen een massa te geven? IJkinvariantie is | |
[pagina 92]
| |
dan bij benadering goed. Zoiets hebben we in de natuur meer gezien. Er zijn allerlei symmetrieën die slechts bij benadering gelden. Veltman verdeelde de termen in de Yang-Millsvergelijkingen in ijkinvariante termen en slechts één niet-ijkinvariante term. De rekenregels die je dan krijgt, waren al eens bestudeerd. Richard Feynman had zich er al eens op geworpen. Maar Feynmans motivatie was wel een heel andere geweest. Een van de allermoeilijkste problemen, misschien wel hét allermoeilijkste probleem in de deeltjesfysica, is het verenigen van de fysica van de quantumdeeltjes met de regels van Einsteins theorie van de zwaartekracht. Feynman wilde zijn krachten er wel eens op proberen, maar merkte dat de eenvoudigste berekeningen in die theorie algauw tot lange en onoverzichtelijke formules leiden. In een mum van tijd heb je hele rollen behangpapier met formules volgeschreven en zie je door de bomen het bos niet meer. Ditmaal was het Gell-Mann die voor Feynman een nuttige suggestie had. Waarom probeer je niet eerst de Yang-Millstheorie? Die is technisch veel eenvoudiger en het fundamentele principe, ijkinvariantie, lijkt veel op de coördinateninvariantie van de zwaartekrachtstheorie. Alleen die massaloze deeltjes in de Yang-Millstheorie zijn vervelend. Feynman slingerde er zonder veel scrupules een massaterm tegenaan en ging aan het rekenen. Feynman was een kei in het vereenvoudigen van ingewikkelde berekeningen en argumenten. Hij ontdekte dat je de rekenregels in een veel eenvoudiger vorm kon gieten door de invoering van zogenaamde ‘spookdeeltjes’. Als deeltjes botsen, is de ‘uit-toestand’ het resultaat van allerlei krachten en effecten. Als je de diverse termen op een bepaalde manier bij elkaar veegt, kunnen de ‘Feynmanregels’ heel eenvoudig worden, maar is het net alsof er extra deeltjes een bijdrage leveren. Deze spookdeeltjes komen echter alleen maar tijdelijk in de beschrijving voor. Wat er na de botsing overblijft, zijn alleen de deeltjes die de experimentator kan waarnemen: de ‘fysische’ deeltjes. Feynman maakte zijn werk niet af. Als je na de eerste reeks | |
[pagina 93]
| |
van correctietermen naar de volgende correcties kijkt, wordt de zaak uiterst ingewikkeld. Hij publiceerde zijn resultaten alleen door een lezingencyclus te geven tijdens een zomerschool in Polen. Aantekeningen die daarvan werden gemaakt kwamen in het wetenschappelijke tijdschrift Acta Physica Polonica. Het was niet zo gemakkelijk meer eruit op te maken hoe Feynman zijn resultaten precies had verkregen. Een van de aanwezigen bij Feynmans lezingen in Polen was Bryce De Witt (zoals de naam zegt, is hij een Amerikaan met Nederlandse voorouders). De Witt was niet zozeer in de Yang-Millstheorie geïnteresseerd als wel in het probleem van de quantumzwaartekracht. Het is aardig in het conferentieverslag te lezen hoe Bryce probeerde Feynman zover te brengen dat hij nu eens écht duidelijk vertelde hoe hij zijn berekeningen had gedaan. Feynman vond dat het geen zin had lange formules op het bord te schrijven als toch niemand ze kon begrijpen, maar De Witt hield aan. Ten slotte gaf Feynman zich over. ‘Ik kan ook best onbegrijpelijke dingen op het bord krijgen,’ zei hij, en toen volgden er meer details. Uit wat daarna gebeurde, bleek dat De Witt heel goed begreep hoe Feynman te werk was gegaan. Hij ging door waar Feynman was blijven steken. Hij verbeterde de technieken en vond inderdaad de correcte Feynmanregels voor diagrammen met willekeurig veel gesloten lussen. Hij publiceerde alleen het eindresultaat in 1964, maar dit trok niet zo veel aandacht omdat de afleiding er niet bij stond en wij niet konden begrijpen wat er precies stond. Het stond er bovendien nog niet helemaal goed. In 1967 publiceerde hij de volledige afleiding wel, maar het werden drie artikelen die zo lijvig waren dat de moed je al in de schoenen zonk nog voor je begon te lezen. Pas later zouden we gaan begrijpen hoe Bryce De Witt de correcte regels had afgeleid; er waren zelfs elementen in zijn technieken die pas veel later in zwang zouden komen. Stanley Mandelstam in Californië had een geheel eigen bena- | |
[pagina 94]
| |
dering van net probleem. Hij beweerde een nieuwe formulering te hebben van de zwaartekrachts- en Yang-Millstheorie waar ook Feynmanregels uit volgden, inclusief de spookdeeltjes van Feynman. En dan waren er groepen in Leningrad en Moskou. Ludwig D. Faddeev en Victor N. Popov kwamen met (praktisch) dezelfde rekenregels als Mandelstam. Hun argumenten waren weliswaar formeel (en daarom in Veltmans ogen verdacht) maar hun eerste publicatie erover was glashelder en heel goed te begrijpen. Hier konden we mee werken. Maar, het een en ander klopte nog niet. De rekenregels van Mandelstam waren niet precies dezelfde als die van de Russen. En allen hadden ze een factor twee anders dan Feynman. ‘Een kniesoor die daarop let,’ zou Feynman daar later over zeggen. Hij bekommerde zich nou eenmaal nooit om zulke pietluttige details. Nu weten we dat dit verschil kwam doordat Feynmans theorie met een massaterm erin een geheel andere was dan die van De Witt, Mandelstam en de Russen, en dat was de reden waarom Feynman niet verder was gekomen. Het was duidelijk dat de zwaartekrachtstheorie, ondanks het feit dat je misschien de formele regels kon afleiden, in de praktijk onbruikbaar zou blijven vanwege gigantische renormeringsmoeilijkheden. De vooruitzichten voor de Yang-Millstheorie leken daarentegen veel gunstiger, zoals ook later zou blijken. We laten de zwaartekracht voorlopig weer even rusten. Wat Veltman wilde, was een Yang-Millstheorie met een massaterm erin, zodanig dat zij ook renormeerbaar is. Dat de eerste correctietermen wel in orde gebracht konden worden was nu wel duidelijk, maar de daaropvolgende zijn verschrikkelijk lastig en onoverzichtelijk. De vergelijkingen worden niet bijzonder moeilijk maar wel heel lang. Het moest mogelijk zijn deze geestdodende manipulaties met een computer te doen. In feite volgen de hogere correctietermen eenduidig uit de theorie. Wat | |
[pagina 95]
| |
men deed, was eigenlijk niets anders dan het toepassen van de ‘dispersierelaties’ die ik eerder noemde in hoofdstuk 9. Toen eindelijk de computerprogramma's feilloos liepen, volgde er een teleurstelling: de oneindige krachten vallen niet tegen elkaar weg. Dat wil zeggen: de ‘massieve Yang-Millstheorie’ is niet renormeerbaar, en daarom onbruikbaar als theorie voor de zwakke kracht. Hoe komt het nu eigenlijk dat sommige theorieën voor de elementaire deeltjes renormeerbaar zijn en andere niet? Om de situatie een beetje te leren begrijpen voer ik u even terug naar het eerste hoofdstuk. Daar merkten we op dat je de wereld onder een vergrootglas kunt bekijken, en dan blijkt de wereld van het kleine een kopie te zijn van de wereld van het grote. Deze situatie doet zich nu ook voor wanneer we elementaire deeltjes beschouwen. Op kleinere schaal gedragen de deeltjes zich op bijna dezelfde wijze als op grotere schaal (al moeten uiteraard alle afstanden kleiner blijven dan de afmetingen van een atoomkern). Elektromagnetische krachten bijvoorbeeld blijven aan dezelfde vergelijkingen voldoen. En wat we op grotere schaal opvatten als een ‘naakt’ deeltje, zal onder de ‘microscoop’ toch nog omringd blijken te zijn door andere deeltjes zoals fotonen. Om onder de microscoop ook weer een naakt deeltje te zien zou je het nog verder moeten uitkleden. Het is op deze manier dat de filosofie van de renormering werkt: het begrip ‘naakt deeltje’ is slechts relatief. In de praktijk blijkt dus een theorie renormeerbaar te zijn wanneer het aangeklede fysische deeltje dezelfde wetten volgt als een naakt deeltje onder de microscoop. Alleen de massa van een deeltje blijft niet dezelfde wanneer je het onder de microscoop bekijkt (in jargon: een schaaltransformatie uitvoert). De reikwijdte van een kracht lijkt onder de microscoop veel groter; daarmee corresponderend lijkt de massa van een deeltje onder een microscoop veel kleiner. Let wel: deze situatie is dus tegenovergesteld aan die in het dagelijkse leven waar een zandkorreltje veel groter (en dus zwaarder?) | |
[pagina 96]
| |
lijkt als je het onder een microscoop legt. Een consequentie van dit alles is dat ook in een Yang-Millstheorie de massaterm zal wegsmelten wanneer we een schaaltransformatie uitvoeren. Dat betekent dat onder de microscoop de ijkinvariantie weer hersteld wordt. Dit nu is de feitelijke bron van de moeilijkheid waar Veltman op stuitte. Is het vectorpotentiaalveld van Yang en Mills nu wel of niet direct observeerbaar? Onder de microscoop niet maar in het groot wel? Dit is een contradictie waardoor de hele constructie niet goed werkte. 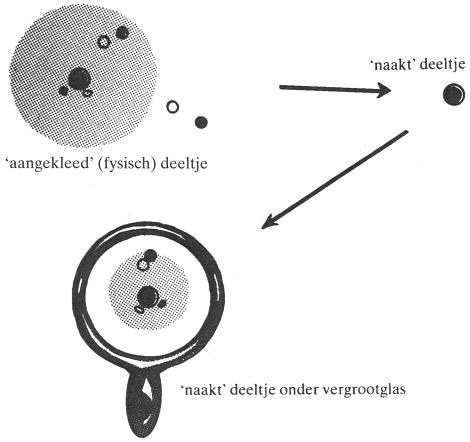
Figuur 9.
|
|

