De bouwstenen van de schepping
(1992)–Gerard 't Hooft–Een zoektocht naar het allerkleinste
[pagina 56]
| |
7 De wonderlijke kaonenIk ben niet van plan alle deeltjes uitvoerig te behandelen, maar de kaonen vormen hierop een uitzondering. Een aantal jaren geleden kon men in iedere speelgoedwinkel een flesje ‘siliconenrubber’ krijgen. Het was wonderlijk spul. Je kon het kneden als klei, en er bijvoorbeeld een balletje van maken. Gooide je dat ergens tegenaan dan bleek het uiterst elastisch terug te kaatsen, heel anders dan je van klei zou verwachten. Liet je dat balletje ergens enige tijd liggen dan zag je tot je verbazing dat het in elkaar zakte en ten slotte meer op een plasje water dan op klei leek, laat staan een kaatsbal. Toch bleef het aanvoelen en kneedbaar als klei. De natuurkundige verklaring van deze ogenschijnlijk tegenstrijdige eigenschappen moet te vinden zijn in de structuur van de moleculen van deze stof. Ik denk dat ze als korte draadjes elkaar steeds korte tijd vasthouden door om elkaar heen te krinkelen maar voortdurend elkaar weer los laten om zich aan andere te hechten. De neutrale kaonen zijn zo mogelijk nog gekker dan siliconenrubber. Ze komen in twee soorten voor, Klang en Kkort. Maar je kunt ook zeggen dat er twee soorten zijn die we K̄o (‘ka-nul’) en K̄o (‘anti-ka-nul’) noemen. Heb je een Ko, dan heb je 50 procent kans dat het een Klang is en 50 procent kans dat het een Kkort is. Hetzelfde geldt als je met een K̄o begon. Anderzijds, als je ‘weet’ dat je een Klang in je vingers hebt, dan is de kans weer 50 procent dat dit zich als een Ko gedragen zal, en 50 procent dat het een K̄o zal blijken te zijn. Ook een Kkort kan zich in 50 procent van de gevallen als Ko en in 50 procent van de gevallen als K̄o voordoen. Anderzijds, een Klang gedraagt zich nooit als een Kkort, en een Ko gedraagt zich nooit als een K̄o! Als de lezer niet zeer goed vertrouwd is met de wonderen van de quantummechanica zal hij of zij van dit alles geen jota begrijpen. Daarom noem ik deze kaonen het siliconenrubber van | |
[pagina 57]
| |
de elementaire deeltjes. Laat ik trachten de mysterieuze mededelingen die ik zojuist deed verder toe te lichten. De gemiddelde levensduur van een Kkort is minder dan 10-10 seconde, zoals in tabel 1 is weergegeven. Sommige zullen een beetje langer leven en andere een beetje korter, maar na pakweg 5 × 10-10 seconde zullen verreweg de meeste Kkort-deeltjes vervallen zijn. De Klang-deeltjes leven gemiddeld zo lang dat de kans dat één van hen reeds na 5 × 10-10 seconde uiteenvalt erg klein is. Als je nu een neutraal kaon hebt dat binnen 5 × 10-10 seconden uiteengevallen is, weet je daarom praktisch zeker dat het een Kkort was. Leeft het daarentegen dan nog steeds, dan is het praktisch zeker een Klang, en mag je verwachten dat het pas na omstreeks 5 × 10-8 seconde uiteen zal vallen. Voor Klang en Kkort nu zijn de quantumgetallen S en I3 niet geldig. Maar als je een kaon produceert via de reactie p + p → Σ+ + p + Ko dan weet je zeker dat het vreemdheidgetal S gelijk +1 moet zijn, want Σ+ heeft S = -1, en de rest heeft S = 0. Nu heeft Ko vreemdheid S = 1, en K̄o heeft S = -1. Dus deze reactie heeft zeker een Ko en niet een K̄o opgeleverd. Laten we een bundel neutrale kaonen door een trefplaatje lopen, dan kunnen deze allerlei interacties ondergaan. Maar de K̄o worden sneller uit de weg geruimd dan de Ko, omdat die met een proton uit het trefplaatje reacties zoals K̄o + p → Σ+ + πo kunnen aangaan, wat bij de andere niet mogelijk is. Figuur 7 laat nu zien wat er kan gebeuren als we een bundel kaonen eerst gedurende 10-8 seconde ongemoeid laten en dan door een trefplaatje laten gaan. Na nog eens 10-8 seconde gaan ze weer door een trefplaatje. | |
[pagina 58]
| |
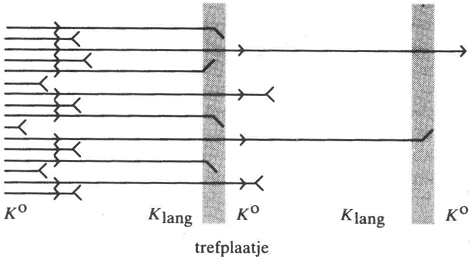
Figuur 7. Geïdealiseerde voorstelling van een experiment met neutrale kaonen. Na hun productie (links) valt (ongeveer) de helft vrij snel uiteen in twee pionen. De andere zijn veel stabieler. We weten nu dat dit Klang is. Van deze wordt nu ongeveer de helft door een trefplaatje geabsorbeerd. De andere lijken immuun; dit zijn vrijwel zeker de deeltjes Ko. Op hun beurt vervallen deze voor de helft zeer snel, de overgeblevene leven weer lang. Dit kan men net zolang herhalen tot de kaonen op zijn.
De deeltjes die geproduceerd zijn, en de deeltjes die door het trefplaatje heen gekomen zijn, zijn (voornamelijk) Ko. De deeltjes die na 10-8 seconde nog steeds niet vervallen zijn, zijn zeker Klang en niet Kkort. De schets is een idealisatie. In een werkelijk experiment vliegen de K-deeltjes alle kanten uit. U kunt zich voorstellen dat dit merkwaardige gedrag bij de ontdekking van deze deeltjes aanleiding gaf tot verwarring. Men dacht aanvankelijk dat er veel meer soorten waren. We hebben hier te maken met een typisch quantummechanisch verschijnsel. De sterke kracht respecteert behoud van vreemdheid, zodat men bij de productie altijd zeker weet of er een Ko of een K̄o is ontstaan. Maar na 10-10 seconde (en dat is veel langer dan de duur van het productieproces zelf, ongeveer 10-24 | |
[pagina 59]
| |
seconde!) doet de zwakke kracht zich voelen. Deze nu trekt zich niets van S of I3 aan. Er vinden overgangen plaats van het type Ko ↔ K̄o en dit heen en weer huppelende systeem kan dit op twee manieren doen. Dat zijn de ‘quantumtoestanden’ Klang en Kkort. Wat er namelijk gebeurt, is dat zowel Ko als K̄o in twee pionen uiteen kunnen vallen, maar er vindt ‘interferentie’ plaats. Als de twee bronnen, Ko en K̄o, met elkaar in de pas lopen, is er positieve interferentie. De piongolven versterken elkaar en het deeltje valt snel uiteen. Het was een Kkort. Maar als de interferentie uitdovend is, kan het systeem niet in twee pionen vervallen. Het is dan een Klang. De kansen zijn steeds 50/50. Klang kan wél in drie pionen uiteenvallen, maar dat duurt veel langer. Vandaar. Omdat quantummechanica een moeilijk vak is, verwacht ik eigenlijk niet dat deze uitleg geheel toereikend is. Dat is niet zo heel erg. U kunt ook met siliconenrubber spelen zonder te begrijpen hoe het werkt. Het is niet de bedoeling de lezer het gevoel te geven dat hij ‘dom’ is om zelf heel geleerd over te komen. Quantummechanica is een specialisme waarvoor niet alleen veel studie maar ook een zeker gewenningsproces nodig is, waarvoor ik u al waarschuwde in mijn voorwoord. Er is nog veel meer te beleven aan de neutrale kaonen. Om dat uit te leggen moet ik eerst iets meer vertellen over die zwakke kracht. Zij overtreedt namelijk een aantal natuurwetten, zoals we hebben gezien: vreemdheid en isospin zijn niet behouden. Niettemin zijn er andere behoudswetten die wel worden gerespecteerd. We zullen dikwijls spreken van behoud van symmetrie. Een uiterst belangrijke symmetrie voor elementaire deeltjes is spiegelsymmetrie. Daarvoor vergelijken we deeltjes met hun spie- | |
[pagina 60]
| |
gelbeeld. Vóór 1956 was men er altijd van uitgegaan dat ieder natuurverschijnsel de natuurwetten even goed respecteert als het spiegelbeeld van dat verschijnsel. Een gevolg daarvan zou zijn dat als een stel deeltjes op een spiegelsymmetrische manier tegen elkaar botsen, de spiegelsymmetrie aanwezig zou moeten blijven. De ontdekking dat vele deeltjes heel anders zijn dan hun spiegelbeeld werd gedaan door twee Chinese natuurkundigen,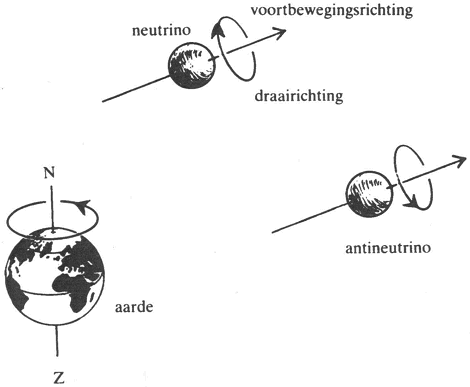
Figuur 8.
Tsung Dao Lee en Chen Ning Yang, niet lang nadat ze naar de Verenigde Staten waren geëmigreerd. Het bleek dat de zwakke kracht onderscheid maakt tussen links en rechts. Dat onderscheid is het meest markant bij het neutrino. Neutrino's hebben slechts een uiterst geringe rustmassa, zodat ze zich meestal ge- | |
[pagina 61]
| |
dragen als een foton, dat wil zeggen ze bewegen zich praktisch even snel voort als het licht. Nu draaien neutrino's daarbij ook nog om hun as (ze hebben spin ½). Als we nu eens ‘noordpool’ en ‘zuidpool’ definiëren net als bij de draaiende aarde, dan heeft het neutrino de bijzonderheid dat het altijd bij zijn ontstaan zijn zuidpool in de richting heeft waarin het beweegt, en de noordpool achter zich. Neutrino's waarbij dat andersom is zijn nog nooit waargenomen. De Zweedse natuurkundige Cecilia Jarlskog vergeleek neutrino's daarom met vampiers: ze hebben geen spiegelbeeld! Hun spiegelbeeld is een natuurkundige onmogelijkheid. Nu is mijn kennis van de vampirologie beperkt. Misschien is het zo dat als u een vampier bent, u misschien met heel veel moeite toch nog een vaag spiegelbeeld in uw spiegel kunt ontwaren. Pas in de jaren negentig kon men vaststellen dat neutrino's een geringe hoeveelheid rustmassa hebben, hetgeen impliceert dat ze wat langzamer gaan dan het licht, en daardoor in principe in staat moeten zijn andersom te draaien. In hoofdstuk 18 kom ik terug op het verkeerd om draaiende neutrino. Wel heeft het antineutrino altijd zijn noordpool vóór zich. Dit is het deeltje dat we aangeven met v̄e of v̄μ. Het blijkt dat alle deeltjes heel veel lijken op het spiegelbeeld van hun antideeltjes. Het verval van het Kkort in twee pionen is wel volledig spiegelsymmetrisch. Dit leek niet te rijmen met het productieproces van de kaonen, tenzij er gedurende het verval een kracht aanwezig was die de symmetrie verstoorde. Het argument hiervoor is weer een moeilijk quantummechanisch verhaal. Als ik het spiegelbeeld bereken van het verval van Ko (óf K̄o) in twee pionen ontdek ik dat dit door interferentie het verval van het oorspronkelijke deeltje geheel zou uitdoven, tenzij het spiegelbeeld anders is. Kortom, uit het feit dat neutrale kaonen überhaupt in twee pionen kunnen uiteenvallen, concludeert men dat spiegelsymmetrie bij de zwakke kracht niet geldt. Dat betekent dat er een schroefzin zit in de zwakke kracht. | |
[pagina 62]
| |
Wel weten we dat de emissie van pionen door enerzijds Ko en anderzijds K̄o geheel kan weg-interfereren. Hier nu kan men uit concluderen dat een deeltje wél hetzelfde doet als het spiegelbeeld van zijn antideeltje. Dit noemen we nu de PC-symmetrie van de zwakke kracht. Spiegeling (‘pariteit’) geven we aan met een P, vervanging van een deeltje door het antideeltje (‘conjugatie’) met de letter C. Alleen de combinatie PC is een symmetrie van de zwakke kracht, niet P en C afzonderlijk. Maar nu is er nog iets aan de hand. We hebben vastgesteld dat de PC-symmetrie er de oorzaak van is dat door uitdovende interferentie het Klang nooit in twee pionen kan uiteenvallen. James Christenson, James Cronin, Val Fitch en René Turlay besloten deze mededeling te toetsen met een experiment. Om nauwkeurig te kunnen meten, waren de sporadische K-deeltjes die hoog in de atmosfeer in ballonexperimenten werden gemeten niet geschikt. Met kaonen die in versnellers worden geproduceerd, kun je veel beter werken. (Val Fitch zei later dat hij dat wel jammer vond; hij zat liever in de bergen dan onder de grond.) Na zeer uitvoerig meten, en vooral checken, ontdekten deze experimentatoren in 1964 dat gemiddeld 3 van de 1000 Klang-deeltjes tóch in twee pionen uiteenvalt! Het knappe van het experiment was dat zij er zich van konden verzekeren dat het geen Kkort kon zijn geweest, en vooral dat er geen derde deeltje was geweest dat wellicht aan de aandacht kon zijn ontsnapt. Pas na een half jaar controleren en analyseren hadden ze zich hiervan overtuigd. Het interferentieverschijnsel dat ik noemde is niet honderd procent waterdicht, er lekt wat! Wat we hieruit moeten opmaken, is dat ook de wet van behoud van PC-symmetrie door de zwakke kracht heel lichtjes overtreden wordt. Maar je kunt ook zeggen dat er nóg een kracht is, een superzwakke kracht, die er louter op gericht is PC-symmetrie te saboteren. We zullen later zien dat we weliswaar deze kracht in onze natuurbeschrijving kunnen opnemen, | |
[pagina 63]
| |
maar dat de diepere reden voor het bestaan van deze kracht voorlopig nog een raadsel zal blijven. In 1980 kregen Cronin en Fitch, de leiders van het experiment, voor hun ontdekking de Nobelprijs. Er is overigens nog een symmetrie die met dit alles verband houdt: tijdsomkering, T. Je kunt het verloop van een natuurverschijnsel terugwaarts volgen in de tijd, bijvoorbeeld door een film ervan achteruit af te draaien. Als we nu tegelijk spiegelen (P), lading omkeren (C) en de tijd omkeren (T) blijven de natuurwetten exact dezelfde. Dit kan men met ingewikkelde redeneringen uit de theorie afleiden. Je kunt het ook experimenteel toetsen, bijvoorbeeld door na te gaan of de rustmassa van een deeltje wel precies dezelfde is als die van zijn antideeltje. Afwijkingen zijn nog nooit geconstateerd. Dat vonden de experimentatoren jammer. Ze hadden maar wat graag de theorie in zijn hemd gezet. De ontdekking dat PC-symmetrie niet exact door de natuurwetten wordt gerespecteerd, wordt vaak in verband gebracht met een probleem in de kosmologie of ‘heelalkunde’. De enorme aantallen hemellichamen in ons heelal bestaan alle uit protonen, neutronen en elektronen. Men weet praktisch zeker dat er geen enkele ster of sterrenstelsel is die uit ‘antimaterie’ bestaat: antiprotonen, antineutronen en positronen.Ga naar voetnoot1 Dat is gek. Waarom dit gebrek aan symmetrie? Welnu, in het allereerste beginstadium van het heelal was er misschien helemaal geen verschil tussen de hoeveelheden materie en antimaterie. Er was slechts een zeer hete ‘soep’ van uiterst energetische oerdeeltjes. Daarna kunnen er natuurkrachten werkzaam zijn geweest die | |
[pagina 64]
| |
hieruit de ons bekende deeltjes deden condenseren, maar met een lichte voorkeur voor materie in plaats van antimaterie. Die krachten zouden de wet van behoud van baryongetal moeten overtreden, maar dat is geen probleem; we zullen later zulke krachten tegenkomen. Men weet echter dat zulke effecten ook niet zouden kunnen optreden zonder ook PC-symmetrie te verbreken, als we mogen aannemen dat het heelal min of meer spiegelsymmetrisch is. Nu we weten dat PC-symmetrie niet geldt, kan men heelalmodellen bedenken waarin het heelal begon als zijnde klein en leeg, en vanzelf evolueerde tot wat het nu is. Dit is een veld van onderzoek dat bezig is zich te verheffen van sciencefiction tot een belangwekkende tak van wetenschap. Meer hierover in hoofdstuk 30. |
|

