Logo DBNL
De bouwstenen van de schepping (1992)

De bouwstenen van de schepping

(1992)–Gerard 't Hooft–rechtenstatus Auteursrechtelijk beschermd

Een zoektocht naar het allerkleinste


Vorige Volgende

6 Leven en dood

Als we spreken van de levensduur van een deeltje bedoelen we daarmee altijd de gemiddelde levensduur. Een deeltje dat niet absoluut stabiel is heeft op ieder moment dezelfde kans dat het uiteenvallen zal. Sommige leven dus langer dan andere, maar de gemiddelde levensduur is een karakteristieke eigenschap van een deeltjessoort.

Men hanteert ook weleens het begrip ‘halfwaardetijd’. Als we een groot aantal identieke deeltjes hebben, is de halfwaardetijd de tijd die het duurt totdat de helft van deze deeltjes is uiteengevallen. De halfwaardetijd is 0,693 maal de gemiddelde levensduur.

U ziet in de tabel dat sommige deeltjes een veel langere gemiddelde levensduur hebben dan andere. De vervalstijden lopen enorm uiteen. Het neutron leeft meer dan tien biljoen keer zo lang als het sigma-plus, en het sigma-plus leeft meer dan een miljard keer langer dan het sigma-nul. Maar als je bedenkt dat hun ‘natuurlijke’ tijdsschaal (de snelheid waarmee hun quantummechanische bewegingen verlopen) ongeveer 10-24 seconden is, kun je gerust stellen dat al deze deeltjes zeer stabiel zijn. In het vakjargon heten zij dan ook ‘stable particles’.

Hoe wordt de levensduur van een deeltje bepaald? Deeltjes die nogal lang leven, zoals het neutron en het muon, moeten worden opgevangen, liefst in groten getale, waarna men het verval elektronisch detecteert. Het neutron laat zich niet gemakkelijk vangen, zodat nauwkeurige leeftijdsbepaling daarvan heel moeilijk is.

Deeltjes met een levensduur in de buurt van 10-10 tot 10-8 seconden werden vroeger in een bellenvat geregistreerd; tegenwoordig gebeurt dit vaak in een dradenkamer. In een bellenvat laat een langsschietend elektrisch geladen deeltje een spoor van belletjes achter, dat dan wordt gefotografeerd. Een draden-

kamer bevat een groot aantal elkaar kruisende dunne metaaldraadjes waarop elektrische spanning staat. Een elektrisch geladen deeltje veroorzaakt een reeks van ontladingen (vonkjes) tussen de draden waar het langskomt. Deze worden dan rechtstreeks elektronisch geregistreerd. Het voordeel daarvan is dat het signaal linea recta de computer in gaat.

Een elektrisch neutraal deeltje laat nooit direct een spoor na, maar als het interacties vertoont (het valt uiteen in geladen deeltjes of het botst tegen deeltjes in het apparaat), dan registreert men dit natuurlijk wel. Men plaatst bovendien meestal het gehele apparaat tussen de poolschoenen van een krachtige magneet. Hierdoor gaan de geladen deeltjes een krom spoor volgen, en aan de kromming is dan af te lezen hoe snel het deeltje ging. Maar omdat deze kromming ook van de massa van het deeltje afhangt, is het soms nuttig de snelheid ook nog op een andere manier te meten.

Meestal bewegen de deeltjes zich met snelheden die niet ver onder de lichtsnelheid zitten. Gedurende hun korte leventje leggen ze daardoor toch nog enige centimeters af. Uit de gemiddelde lengte van zo'n spoor wordt dan de gemiddelde levensduur afgeleid. Het gebied tussen 10-13 en 10-20 seconden is echter heel moeilijk direct te meten. Men leidt de levensduur af langs indirecte weg door de krachten waarmee het deeltje in andere kan overgaan in andere deeltjesreacties te meten. Dan kun je de levensduur uitrekenen. U ziet dat de experimentatoren met eindeloos veel vernuft een heel arsenaal van technieken hebben opgebouwd om zoveel mogelijk over onze deeltjes te weten te komen. Bij sommige van dit soort metingen is het uiterst moeilijk grote nauwkeurigheid te bereiken. De getallen die u in tabel 1 ziet zijn de resultaten van vele, vele manjaren precisiemeetwerk. Ik heb de laatst gepubliceerde gegevens hier weergegeven.

Dat de meeste deeltjes een gemiddelde levensduur hebben van 10-8 seconden of iets dergelijks, betekent dat hun golfjes

meer dan 100.000.000.000.000 trillingen mogen uitvoeren tot ze een keer uiteenvallen. We kunnen daarom gerust zeggen dat de kracht die voor dit uiteenvallen verantwoordelijk is uiterst zwak is. Ze zijn te vergelijken met een stemvork die pas na 100.000.000.000.000 trillingen uitdooft omdat er een uiterst zwakke wrijvingskracht is. De kracht die deze deeltjes laat uiteenvallen zijn we gaan kennen als de ‘zwakke kracht’.

Het uiteenvallen van het neutron schrijven we ook toe aan de zwakke kracht, hoewel de levensduur van het neutron veel langer is (gemiddeld een kwartier). Sterker nog, sommige radioactieve atoomkernen die ook zwak uiteenvallen, kunnen daar vele miljoenen of zelfs miljarden jaren over doen. Maar de reden voor deze veel langere levensduur is dat de hoeveelheid massa die in bewegingsenergie kan worden omgezet in deze gevallen heel klein is.1 Kennelijk is dus niet alleen de sterkte van een kracht, maar zeker ook de hoeveelheid vrijkomende energie bepalend voor de vervalsnelheid van een deeltje.

Als de zwakke kracht er niet geweest was, zouden dus de meeste deeltjes in de tabel helemaal stabiel zijn. De kracht verantwoordelijk voor het verval van πo, η en Σo is de elektromagnetische kracht. U ziet dat deze deeltjes een veel kortere levensduur hebben; de elektromagnetische kracht is dan ook veel sterker dan de zwakke kracht.

Deze hele wirwar van subatomaire deeltjes was in de jaren vijftig en zestig ten tonele verschenen. ‘Als ik dit had kunnen voorzien, was ik plantkunde gaan studeren!’ verzuchtte Enrico Fermi, de beroemde Italiaanse natuurkundige.

Ten slotte waren er in 1970 ook nog hele series hadronen bekend met veel grotere spinwaarden. Deze echter kunnen al

__________

De sterke kracht

•De sterke kracht werkt alleen in op de deeltjesgroep die we hadronen noemen. Deze krijgen hierdoor een ingewikkelde inwendige structuur.
Tot omstreeks 1972 kenden we slechts de strenge symmetrieregels van deze sterke kracht, maar konden we de krachtwetten niet nauwkeurig formuleren.
•De reikwijdte van de kracht is niet verder dan de straal van een lichte atoomkern (ca. 10-13 cm).
•De kracht is sterk. Deeltjes die door toedoen van de sterke kracht kunnen uiteenvallen, doen dat dan ook zeer snel. Deze noemen we ‘resonanties’. Een voorbeeld is de Δ-resonantie, met een gemiddelde levensduur van slechts 0,6 × 10-23 sec. Als twee hadronen dichter dan ca 10-13 cm bij elkaar komen is de kans dat ze botsen vrijwel zeker.
•De pionen (spin 0, massa 135 tot 140 MeV) werden tot omstreeks 1972 als dragers van de sterke kracht beschouwd. De sterke aantrekkingskracht tussen bijvoorbeeld twee protonen wordt voornamelijk veroorzaakt door de uitwisseling van pionen.
Thans zeggen we dat dit alleen maar komt doordat de pionen toevallig de lichtste hadronen zijn. Net als alle andere hadronen zijn ze uit ‘quarks’ opgebouwd. We zien nu de sterke krachten tussen de hadronen als uitvloeisel van een nog sterkere kracht tussen de quarks. De dragers van die nog sterkere kracht zijn de gluonen, waarover meer in hoofdstuk 13.

__________

door toedoen van de sterke kracht uiteenvallen. Daardoor hebben ze alle een uiterst korte levensduur (alle in de buurt van 10-23 seconde). Het is meestal gemakkelijk na te gaan welke hadronen door toedoen van sterke krachten uiteen kunnen vallen. Je hoeft slechts een aantal deeltjes te kunnen aanwijzen in de tabel die zodanig zijn dat al hun ladingen (dus ook S en I3) opgeteld dezelfde zijn als die van het oorspronkelijke deeltje en bovendien de massa's opgeteld kleiner zijn dan die van het oorspronkelijke deeltje. Dan is er geen enkele belemmering meer voor het oorspronkelijke deeltje om in deze combinatie van deeltjes over te gaan. De overtollige massa wordt in bewegingsenergie omgezet.

Bij deeltjes met een zo korte levensduur heeft het uiteenvallen een effect op de energie waarmee het deeltje geproduceerd werd. Vergelijken we het deeltje weer met een stemvork, dan betekent het uiteenvallen ervan dat de stemvork wordt gedempt. Maar dan wordt de trillingsfrequentie (die direct met de energie correspondeert) minder precies, en de resonantiecurve van de stemvork wordt minder scherp. We noemen zo'n deeltje een resonantie, en de levensduur is direct uit de resonantiecurve af te leiden.

Een bekend voorbeeld van een resonantie is het delta (Δ), waarvan er vier soorten zijn: Δ-, Δo, Δ+ en Δ++. De laatste heeft een dubbele elektrische lading. De massa's zijn bijna gelijk: alle ongeveer 1230 MeV. De vreemdheid S is nul en I3 loopt van -1½ tot +1½; baryongetal B is 1. Dit alles betekent dat ze in een proton of een neutron en een pion vervallen kunnen, bijvoorbeeld: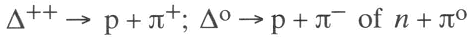

illustratie

Telt u de (rust)massa's bij elkaar op, dan ziet u dat er meer dan 150 MeV overblijft. Dit wordt in bewegingsenergie omgezet.

Er zijn mesonische en baryonische resonanties. De deltareso-

nanties zijn baryonisch (we zullen later de mesonische resonantie ϱ (rho) tegenkomen). Rond 1970 kende men vele tientallen resonanties en had het er alle schijn van dat er eigenlijk oneindig veel zijn, ieder met wat meer massa dan de voorafgaande, maar met een zo korte levensduur dat hun uiterst kortstondige aanwezigheid niet meer valt vast te stellen.

U kunt resonanties beschouwen als deeltjes in een ‘aangeslagen toestand’. Het zijn replica's van de bestaande hadronen, maar meestal harder om hun as draaiend of op een andere manier aan het trillen gebracht, zoals men een gong aan het trillen brengt door ertegen te slaan. En zoals een gong geluid uitzendt en daardoor geleidelijk aan ophoudt met trillen, zo zendt een resonantie pionen uit, waarbij het dan overgaat in een stabiel(er) deeltje.


Vorige Volgende