|
| |
| |
| |
VIII. Het producentengedrag
1. Inleiding
Uit de theorie van het consumentengedrag is de collectieve vraagfunctie afgeleid. Deze functie geeft de hoeveelheid aan die de consumenten tezamen bij uiteenlopende prijzen vragen. In dit hoofdstuk zal worden nagegaan, welke hoeveelheden de producenten bij uiteenlopende prijzen zullen aanbieden. Thans zal dus de collectieve aanbodfunctie worden afgeleid.
Bij deze afleiding worden de beschikbare hoeveelheden van de produktiefactoren en de stand van de technische kennis als gegeven aangenomen. Deze beide gegevens behoren tot de data van de economie. De producenten laten zich bij de vaststelling van de produktie-omvang onder meer leiden door hun kosten. Daarom zullen wij eerst moeten nagaan hoe de kosten zich ontwikkelen als de produktie stijgt. Het verband tussen kosten en produktie-omvang heet de kostenfunctie.
Om een inzicht te krijgen in de kostenfunctie moeten wij eerst onderzoeken hoe de fysieke omvang van de produktie verandert als één van de produktiefactoren varieert. Meestal wordt het voorbeeld genomen van de boer, die een stuk grond van bepaalde afmetingen heeft en achtereenvolgens 1,2, 3, .... arbeiders aan het werk zet. Er kan dan worden afgeleid hoe de totale opbrengst - bv. uitgedrukt in hl. graan - zich ontwikkelt.
| |
Conclusie
Een analyse van het producentengedrag noodzaakt, de kostensituatie van een bedrijfshuishouding te bestuderen. De kostensituatie wordt in de eerste plaats bepaald door het verband tussen de fysieke omvang van de produktie en de hoeveelheid van de variabele produktiefactor.
| |
2. De wet van de toe- en afnemende meeropbrengst
De ervaring heeft geleerd, dat, wanneer aan een constant gehouden produktiefactor (grond) successievelijk een variabele produktiefactor (arbeid) wordt toegevoegd, de totale opbrengst (graan) eerst meer en
| |
| |
later minder dan evenredig stijgt met de variabele factor. In het bijgaande staatje is dit gedemonstreerd.
| Aantal arbeiders |
Totale opbrengst in hl. |
Aantal arbeiders |
Totale opbrengst in hl. |
| 1 |
5 |
6 |
49 |
| 2 |
12 |
7 |
54 |
| 3 |
21 |
8 |
57 |
| 4 |
31 |
9 |
58 |
| 5 |
43 |
10 |
58 |
Dit verband tussen de totale produktie en de variabele produktiefactor geldt niet allen voor de landbouw, maar ook voor de industrie. Men kan ook zeggen, dat de gemiddelde opbrengst eerst stijgt en later daalt, zoals uit het volgende staatje blijkt:
| Aantal arbeiders |
Gemiddelde opbr. in hl. |
Aantal arbeiders |
Gemiddelde opbr. in hl. |
| 1 |
5.0 |
6 |
8.1 |
| 2 |
6.0 |
7 |
7.7 |
| 3 |
7.0 |
8 |
7.1 |
| 4 |
7.7 |
9 |
6.4 |
| 5 |
8.6 |
10 |
5.8 |
Tenslotte kan hetzelfde verband ook worden geformuleerd met behulp van het begrip meeropbrengst. Onder de meeropbrengst verstaat men de vergroting van de totale opbrengst door één arbeider meer te werk te stellen. Deze meeropbrengst is in het onderstaande overzicht aangegeven:
| |
| |
| Aantal arbeiders |
Meeropbrengst in hl. |
Aantal arbeiders |
Meeropbrengst in hl. |
| 1 |
5 |
6 |
6 |
| 2 |
7 |
7 |
5 |
| 3 |
9 |
8 |
3 |
| 4 |
10 |
9 |
1 |
| 5 |
12 |
10 |
0 |
Men kan dus ook zeggen, dat onder de hierboven aangegeven omstandigheden de meeropbrengst eerst toeneemt en voorbij een zeker punt weer afneemt. Alle drie gegeven omschrijvingen zijn gelijkwaardige formuleringen voor de wet van de toe- en afnemende meeropbrengst. Deze ervaringsregel voor de produktie ligt ten grondslag aan de gedaante van de kostenfuncties. Om dit toe te lichten is eerst in de figuren 11 en 12 het verloop aangegeven van de totale-, gemiddelde- en meeropbrengst in afhankelijkheid van de variabele produktiefactor.
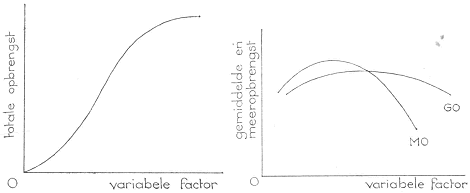
Fig. 11
| |
| |
| |
Conclusie
De wet van de toe- en afnemende meeropbrengst beschrijft de samenhang tussen de fysieke opbrengst en de hoeveelheid van de variabele produktiefactor.
| |
3. De totale kostenfunctie
De in de vorige paragraaf besproken ervaringsregel kan ook omgekeerd worden geformuleerd. De vereiste hoeveelheid van de variabele factor neemt eerst minder en later meer dan evenredig toe met de totale fysieke opbrengst. In het begin vereist een extra eenheid eindprodukt minder van de variabele factor dan in een later stadium. In figuur 13 is dit getekend. Horizontaal is de totale fysieke opbrengst en verticaal de vereiste hoeveelheid van de variabele factor afgebeeld.
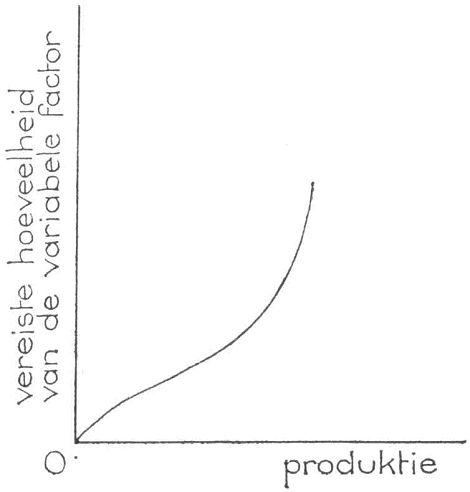
Fig. 13
Deze formulering van de wet van de toe- en afnemende meeropbrengst gaat al in de richting van de kostenfuncties. Er staat immers aangegeven, wat technisch moet worden opgeofferd om een bepaald quantum eindprodukt te krijgen. Teneinde geldelijke kosten te krijgen moet rekening worden gehouden met de prijs van de variabele factor.
| |
| |
Als de variabele factor de menselijke arbeid is, moet het loon worden ingevoerd om het bedrag te vinden dat nodig is om een bepaalde hoeveelheid eindprodukt te krijgen. Door immers het aantal arbeiders te vermenigvuldigen met het loon, ontstaat het loonbedrag dat moet worden betaald. Dit zijn de variabele produktiekosten. Nemen wij aan, dat het loon steeds ƒ 100, - per week is, onafhankelijk van de vraag of er veel of weinig arbeiders te werk zullen worden gesteld. De producent is dan weer hoeveelheidsaanpasser; de prijs (het loon) is gegeven, hij past de gevraagde hoeveelheid aan. In dat geval wordt de vorm van de kromme uit figuur 13 niet beïnvloed door de vermenigvuldiging van de vereiste hoeveelheid arbeid met het loonbedrag ad. ƒ 100. - . Wij kunnen dan de totale variabele kosten als functie van de produktie-omvang tekenen zoals in figuur 14 is gedaan. In deze figuur is ook een rechte evenwijdig aan de horizontale as getekend. Deze lijn stelt de vaste kosten voor, die een gevolg zijn van het aanwenden van de constante produktiefactor.
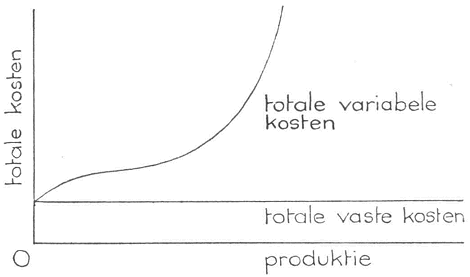
Fig. 14
De vaste kosten reageren niet op de produktie-omvang, de variabele wel. De totale kostenfunctie bestaat dus uit de totale variabele kosten en de totale vaste kosten.
| |
Conclusie
Uit de wet van de toe- en afnemende meeropbrengst kan door omkering de gedaante van de totale kostenfunctie worden afgeleid. Daarbij moet wel de onderstelling worden gemaakt, dat de producent die de produktiefactor vraagt, hoeveelheidsaanpasser is.
| |
| |
| |
4. De gemiddelde en marginale kosten
Onder de gemiddelde totale kosten verstaat men de totale kosten (vaste en variabele), gedeeld door de produktie-omvang. Gezien het verloop van de totale kostenfunctie zal de gemiddelde kostenfunctie eerst dalen en later weer stijgen. Er is dus een minimumpunt.
In figuur 15 is deze kromme getekend.
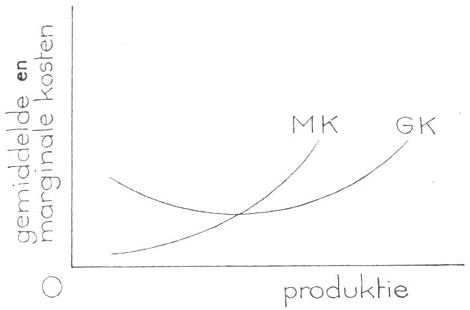
Fig. 15
De figuur toont nog een tweede curve namelijk die van de marginale kosten. Onder de marginale kosten verstaat men de extra kosten die moeten worden gemaakt om de produktie met één eenheid uit te breiden. Juist deze marginale kosten zijn van belang, omdat een ondernemer bij zijn beslissingen steeds zal letten op extra voordeel en extra kosten. De marginale of grenskosten zijn uitsluitend afhankelijk van de variabele kosten, omdat de vaste kosten per definitie niet veranderen als de produktie-omvang verandert.
Omtrent het verloop van de grenskosten ten aanzien van de gemiddelde kosten valt nog het volgende op te merken. Zolang de gemiddelde kosten dalen, moeten de grenskosten beneden de gemiddelde kosten liggen. De gemiddelde kosten stijgen, wanneer de grenskosten boven de gemiddelde kosten liggen. Hieruit volgt, dat de grenskostencurve gaat door het laagste punt van de gemiddelde kostenkromme, omdat daar de gemiddelde kosten noch stijgen noch dalen.
In-het onderstaande staatje is het verloop van de totale variabele, gemiddelde en marginale kosten aangegeven, indien de produktieomvang toeneemt.
| |
| |
| Produktieomvang |
Totale variabele kosten |
Gemiddelde variabele kosten |
Marginale kosten |
| 1 |
ƒ 11.- |
ƒ 11.- |
ƒ 11.- |
| 2 |
20.- |
10.- |
9.- |
| 3 |
28.- |
9.33 |
8.- |
| 4 |
35.- |
8.75 |
7.- |
| 5 |
40.- |
8.- |
5.- |
| 6 |
46.- |
7.66 |
6.- |
| 7 |
54.- |
7.71 |
8.- |
| 8 |
64.- |
8.- |
10.- |
| 9 |
78.- |
8,66 |
14.- |
| 10 |
92.- |
9.20 |
14.- |
Als men de in deze tabel vervatte gegevens in grafieken weergeeft en de punten met elkaar verbindt, krijgt men curven zoals in de figuren 14 en 15 getekend. Tevens blijkt dan, dat de curve van de marginale kosten door het laagste punt van de kromme der gemiddelde kosten gaat.
Terwijl in de theorie van het consumentengedrag de hypothese wordt ingevoerd, dat de consument streeft naar maximale behoeftenbevrediging, wordt in de theorie van het producentengedrag aangenomen, dat de ondernemer streeft naar maximale winst. Winst is het verschil tussen de totale opbrengsten en de totale kosten. Wij hebben nu wel een inzicht in de kostensituatie van de ondernemer, maar weten nog niets van zijn opbrengsten. Daartoe moet worden ingegaan op de afzetverhoudingen van de bedrijfshuishouding.
| |
Conclusie
Het vaststellen van de produktie-omvang waarbij de ondernemer maximale winst heeft, vereist zowel kennis van de kosten- als van de opbrengstensituatie.
| |
| |
| |
5. De individuele afzetfunctie
Reeds werd aangenomen, dat de ondernemer hoeveelheidsaanpasser is met betrekking tot de aankoop van arbeid. Of hij nu veel of weinig arbeiders te werk stelt, zo namen wij aan, hij moet steeds hetzelfde loon betalen. Wij zullen nu onderstellen, dat ook de verkoopsituatie zo is, dat hij voor zijn produkt steeds dezelfde prijs ontvangt, onverschillig of hij veel of weinig verkoopt. Dit geldt bij voorbeeld voor een boer die, als gevolg van zijn beperkte aandeel in het totale aanbod, steeds dezelfde prijs voor het graan krijgt, geheel onafhankelijk van de hoeveelheid die hij verkoopt.
De hoeveelheid die een bedrijfshuishouding kan verkopen, is gebaseerd op de vraag naar het produkt dat door de onderneming wordt gemaakt. Met andere woorden: de individuele afzetfunctie, die weergeeft welke hoeveelheden bij uiteenlopende prijzen kunnen worden afgezet, is gebaseerd op de collectieve vraagfunctie. In geval van hoeveelheidsaanpassing is de prijs steeds dezelfde welke hoeveelheid ook wordt afgezet. Figuur 16 toont deze afzetfunctie; horizontaal staat de afzet en verticaal de prijs afgebeeld.
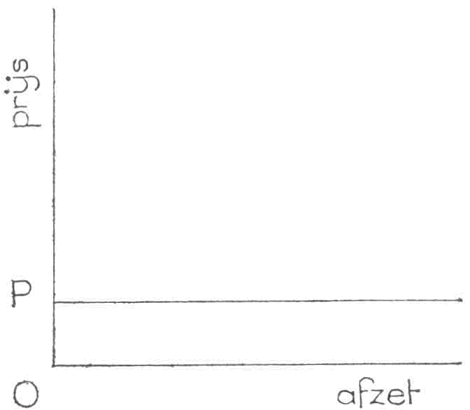
Fig. 16
De individuele afzetfunctie is grafisch een rechte evenwijdig aan de horizontale as. Bij de prijs O P hoort zowel een lage als een hoge afzet. Door de afzet te wijzigen zal men de prijs O P niet beinvloeden.
De totale opbrengst is gelijk aan de verkochte hoeveelheid produkt vermenigvuldigd met de prijs. De gemiddelde opbrengst is dus altijd gelijk aan de prijs; in ons geval O P. Onder de marginale opbrengst
| |
| |
verstaat men de toename van de totale opbrengst wanneer men de verkoop met één eenheid uitbreidt. Als de ondernemer hoeveelheidsaanpasser is, valt de marginale opbrengst dus samen met de gemiddelde opbrengst en de prijs, omdat elke extra eenheid de totale opbrengst doet stijgen met de prijs van één eenheid van het goed. Verkoopt men bv. 10 eenheden tegen een prijs van ƒ 5.- per stuk, dan bedraagt de totale opbrengst ƒ 50.-; de gemiddelde opbrengst is dan ƒ 5.-. Worden 11 eenheden verkocht, dan is de totale opbrengst ƒ 55.- omdat de prijs per stuk ƒ 5.- blijft. De gemiddelde opbrengst is ƒ 5.- terwijl ook de marginale opbrengst hieraan gelijk is.
Het streven naar maximale winst impliceert, dat de bedrijfshuishouding elke eenheid zal produceren die meer oplevert dan kost. Zolang derhalve de marginale opbrengst boven de marginale kosten ligt, wordt de produktie voortgezet. De maximale winst is bereikt, indien marginale opbrengsten en kosten aan elkaar gelijk zijn. Voorbij dat punt overtreffen de marginale kosten immers de marginale opbrengsten, zodat het onverstandig is deze eenheden te produren. Het feit, dat de produktie wordt voortgezet tot het punt waar marginale opbrengsten en kosten aan elkaar gelijk zijn, betekent niet, dat de winst nihil is. Integendeel: op alle voorafgaande eenheden wordt winst gemaakt.
Hoeveel zal de ondernemer nu produceren als de prijs O P bedraagt? Wij weten, dat de curve van de grensopbrengst samenvalt met die van de gemiddelde opbrengst. Om de produktie te bepalen die een maximale winst oplevert moeten wij ook nog de kosten in de beschouwing betrekken. Daarom zijn in figuur 17 naast de gemiddelde en marginale opbrengst ook de gemiddelde en marginale kosten-
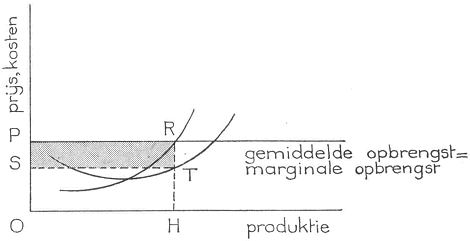
Fig. 17
| |
| |
functies getekend. De produktie waarbij de winst maximaal is, bedraagt O H, omdat voor die produktie marginale opbrengst en marginale kosten aan elkaar gelijk zijn. Merk op, dat voor elke produktie kleiner dan OH, de marginale opbrengst groter is dan de marginale kosten. Voorbij OH geldt het omgekeerde.
Hoe groot de winst is kan worden bepaald door de totale opbrengst en de totale kosten te bepalen. Grafisch wordt de totale opbrengst weergegeven door het oppervlak O H R P en de totale kosten worden in de figuur aangeduid door het oppervlak O H T S, omdat O S = H T de gemiddelde kosten zijn. De winst is dus S T R P. Als de prijs O P is, is de produktie-omvang, waarbij de winst maximaal is, O H.
| |
Conclusie
Voor een hoeveelheidsaanpasser is de afzetfunctie, grafisch uitgedrukt, een rechte, evenwijdig aan de as waarop de afzet staat afgebeeld. Gemiddelde en marginale opbrengst vallen samen. Uitgaande van het streven naar maximale winst kan men dan bij een willekeurige prijs O P de produktie-omvang O H bepalen, die de winst màximaliseert. De produktie-omvang O H heet het aanbod - niet te verwarren met de afzet - bij de prijs O P.
| |
6. De aanbodfunctie
Als de prijs O P is wordt de hoeveelheid O H aangeboden. Deze formulering laat de mogelijkheid toe, dat bij een andere prijs een andere hoeveelheid zal worden aangeboden. Dit is ook inderdaad het geval. Om dit in te zien is figuur 18 ontworpen, waarin verscheidene afzetfuncties zijn getekend. Men ziet gemakkelijk in, dat bij een prijs O P het aanbod O H, bij een prijs O P' het aanbod O H' en bij een prijs O P" het aanbod O H" behoort.
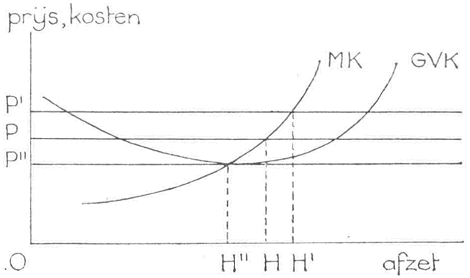
Fig. 18
| |
| |
Er is dus een individuele aanbodfunctie, die aangeeft welke hoeveelheden de individuele aanbieder bij uiteenlopende prijzen aanbiedt. Deze individuele aanbodfunctie valt samen met de marginale kostenkromme, voorzover deze ligt boven het snijpunt met de gemiddelde variabele kostencurve. Als de prijs beneden het minimum van de gemiddelde totale kosten ligt wordt verlies geleden, doch een deel van de vaste kosten wordt nog goed gemaakt. Komt de prijs beneden het minimum van de gemiddelde variabele kosten dan wordt de produktie stopgezet, omdat elke extra eenheid het verlies slechts vergroot.
Uit al de individuele aanbodfuncties kan de collectieve aanbodfunctie worden afgeleid door horizontale optelling. Voor twee aanbieders is dit in figuur 19 gedemonstreerd:
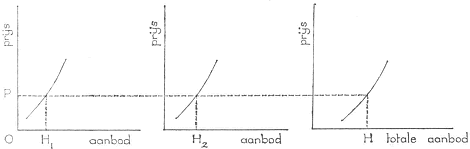
Fig. 19
De collectieve aanbodfunctie geeft aan, welke hoeveelheden door de gezamenlijke aanbieders bij uiteenlopende prijzen worden aangeboden. Evenals voor de collectieve vraagfunctie geldt ook nu de opmerking, dat hiermede niet is aangegeven, welke prijs zal ontstaan. Wij zijn nu slechts op de hoogte van het gedrag van de producenten, dat wil zeggen: wij weten wat zij bij uiteenlopende prijzen zullen aanbieden. De aanbodfunctie stijgt, hetgeen tot uitdrukking brengt, dat bij een hogere prijs door de ondernemers een grotere hoeveelheid zal worden aangeboden.
| |
Conclusie
De onderstelling van de hoeveelheidsaanpassing, die bij het consumentengedrag leidt tot de collectieve vraagfunctie, voert in de theorie van het producentengedrag tot de collectieve aanbodfunctie. Zoals zal blijken wordt uit het samenspel van de collectieve vraag- en de collectieve aanbodfunctie de evenwichtsprijs geboren.
| |
| |
| |
7. Slotopmerkingen
In dit hoofdstuk is het producentengedrag besproken. Uit de wet van de toe- en afnemende meeropbrengst is de gedaante van de kostenfuncties afgeleid. De kostenfuncties kunnen verschuiven door veranderingen in de techniek en door wijzigingen in de prijzen van de produktiemiddelen.
Als de bedrijfshuishoudingen streven naar maximale winst wordt de produktie uitgebreid tot marginale kosten en opbrengsten aan elkaar gelijk zijn. Door de hypothese van de hoeveelheidsaanpassing te handhaven kan men op eenvoudige wijze steeds bij elke prijs de optimale produktie bepalen. Zo ontstond de aanbodfunctie, die bij uiteenlopende prijzen aangeeft, wat de ondernemers zouden aanbieden. Het werkwoord ‘zouden’ is hier belangrijk, omdat, zoals we nog zullen zien, in feite slechts één prijs ontstaat.
Aan de verschijnselen met betrekking tot de produktie is vooral aandacht geschonken door de Klassieke School. Belangrijke vertegenwoordigers waren Adam Smith (1723-1790), David Ricardo (1772-1823), John Stuart Mill (1806-1873) en Jean Baptiste Say (1767-1832). Smith wordt wel eens als de grondlegger van de economische wetenschap beschouwd wegens zijn boek uit 1776: ‘An Inquiry into the Nature and Causes of the Wealth of Nations’.
Afgezien van Say meenden de Klassieken, dat de prijzen overwegend door de produktiekosten werden bepaald. Zij letten derhalve alleen op de aanbodkant en gingen voorbij aan de vraagzijde, die van even groot belang is.
| |
8. Vragen
| 1. | Licht toe, dat de kostenfuncties kunnen verschuiven door de in paragraaf 7 genoemde twee oorzaken. |
| 2. | Waardoor kan de collectieve aanbodfunctie verschuiven? |
| 3. | Geef een grafische afleiding van de individuele aanbodfunctie. Teken daarbij ook de gemiddelde totale kostencurve. |
| 4. | Wat is het verschil tussen de individuele afzetfunctie en de individuele aanbodfunctie? |
|
|