|
| |
| |
| |
VII. Het consumentengedrag
1. Inleiding
Stijging van de effectieve vraag, gevoed door geldschepping en ontpotting, leidt voorbij het bestedingsevenwicht tot prijsstijging. Deze prijsstijging betreft een toename van de absolute prijzen, d.w.z. dat het hier gaat om de absolute bedragen die men voor de goederen moet geven. De inflatoire prijsstijging weerspiegelt de ontwaarding van het geld; de koopkracht van het geld daalt.
Nu is het denkbaar, dat bij gelijkblijvend geldinkomen de totale consumptie zich wijzigt door veranderingen van de prijsverhoudingen van de consumptiegoederen. Als bv. de prijs van peren sterk daalt en die van appelen stijgt, is het niet uitgesloten, dat de consumenten meer peren gaan kopen en minder appelen. Meestal daalt dan het totale bedrag, dat aan consumptie wordt uitgegeven. Een soortgelijke redenering kan men houden voor de investeringsfunctie. Het blijkt dus, dat de consumptie- en de investeringsfunctie kunnen verschuiven door veranderingen in de prijsverhoudingen tussen de goederen. M.a.w. wij moeten niet alleen letten op de absolute prijzen, doch ook op de relatieve prijzen. Daarbij gaat het vooral om de reacties van consumenten en producenten op veranderingen in de relatieve prijzen. Deze reacties beïnvloeden immers de effectieve vraag. Het is derhalve nodig wat dieper in te gaan op de overwegingen van consumenten en producenten bij de bepaling van hun bestedingen. Zo komt de micro-economie ter sprake, die het gedrag van de individuele consumptiehuishouding en de individuele produktiehuishouding analyseert.
| |
Conclusie
De effectieve vraag is mede afhankelijk van de relatieve prijzen. Het onderzoek naar de betekenis van de relatieve prijzen voor de bestedingen noodzaakt dieper in te gaan op het gedrag van de afzonderlijke gezins- en bedrijfshuishouding. Daarmede zijn wij bij de micro-economie beland.
| |
| |
| |
2. Het preferentieschema van de consument
Een consument die koopt, heeft bewust of onbewust verscheidene aankopen tegen elkaar afgewogen en tenslotte een voorkeur, d.i. een preferentie uitgesproken voor het goed dat hij zich aanschaft. De moderne theorie van het consumentengedrag is dan ook gebaseerd op de gedachte, dat de consument preferenties kan uitspreken. Laten wij om dit duidelijk te maken eens aannemen, dat het in een bepaald geval slechts gaat om twee goederen, appelen en peren. De consument zegt bv., dat hij liever 10 appelen en 2 peren heeft dan 9 appelen en 4 peren. Hij spreekt dan een prefentie voor de eerste combinatie van appelen en peren uit. Waarom hij dit doet is een kwestie die in de economie niet ter sprake komt, omdat de behoeftenschema's van de consumenten tot de data van de economie worden gerekend.
De preferentie van de ene combinatie boven de andere betekent, dat de consument aan de ene goederencombinatie een hoger nut toekent dan aan de andere goederencombinatie. Vroeger meende men te kunnen zeggen, hoeveel het nut groter was: men dacht dat het nut meetbaar was. De Italiaanse econoom Pareto (1848-1923) was het daar niet mee eens; hij ging ervan uit, dat de consument de hem voorgelegde goederencombinaties slechts kan rangschikken. Hij kan alleen maar zeggen of hij iets hoger of lager waardeert, zonder daarbij aan getallen te denken.
Een consument die preferenties kan uitspreken, kan ook indifferenties uitspreken. Iemand die kan zeggen, dat hij het ene liever heeft dan het andere kan ook zeggen, dat de ene goederencombinatie hem even lief is als de andere. Het uitspreken van indifferenties voor verschillende goederencombinaties betekent, dat de consument aan al deze combinaties hetzelfde nut toekent.
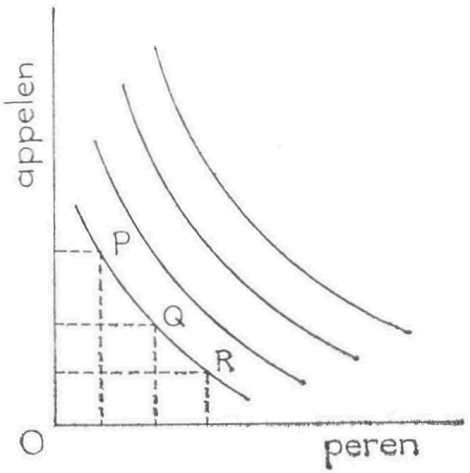
Fig. 6
| |
| |
Als wij op de horizontale as van figuur 6 de hoeveelheid peren afbeelden en op de verticale as de hoeveelheid appelen, dan stelt elk punt in de figuur een bepaalde combinatie van appelen en peren voor. Verbinden wij nu alle punten, die goederencombinaties voorstellen welke voor de consument eenzelfde nut opleveren, dan krijgen wij een indifferentiekromme.
Een iets verder van de oorsprong O verwijderde indifferentiekromme ontstaat, wanneer we letten op goederencombinaties die alle meer nut opleveren dan de eerste. Zo kan men het hele vlak opgevuld denken met indifferentiekrommen.
De vraag, is nu: waarom keert de kromme de bolle zijde naar de oorsprong? Welke onderstelling is hier ingevoerd? Daartoe bekijken wij een s de goederencombinaties P, Q en R op de onderste indifferentiekromme. Terwijl de hoeveelheden peren van P naar Q en van Q naar R met één vermeerderen, neemt de hoeveelheid appelen met een verschillend aantal af. Wat betekent dit? Daar P, Q en R goederencombinaties voorstellen, die eenzelfde nut opleveren, is de consument blijkbaar bereid de eerste keer ter compensatie van het verlies aan appelen met minder peren te volstaan dan de tweede. Nu is de tweede keer zijn voorraad appelen geringer dan de eerste keer, terwijl voor de peren het omgekeerde geldt. We moeten dan ook concluderen, dat de consument het verlies van één appel thans ernstiger vindt dan in de vorige situatie. We zeggen, dat het extra nut -het grensnut - dat een consument toekent aan een eenheid van een voorraad, groter is naarmate de voorraad kleiner is. Uitgaande van de peren kan men ook zeggen, dat de consument aan een extra peer minder nut toekent naarmate hij over een grotere voorraad peren beschikt. Kort geformuleerd: het grensnut van een goed daalt naarmate men over een grotere hoeveelheid van het goed de beschikking heeft.
De onderstelling die is ingevoerd wordt in overeenstemming met de ervaring geacht. De regel, dat binnen een behoefteperiode het grensnut daalt als de voorraad toeneemt, wordt dan ook een ervaringsregel genoemd. Deze regel is reeds in 1854 ontdekt door Gossen en heet daarom de eerste wet van Gossen.
Als er meer dan twee goederen zijn, kan men het preferentieschema niet meer grafisch voorstellen, maar er uiteraard nog wel over spreken. Het gaat dan om het uitspreken van preferenties en indifferenties voor een groot aantal goederen.
| |
| |
| |
Conlusie
Het preferentieschema van de consument, een datum dat uitgangspunt voor de theorie van het consumentengedrag is, kan worden beschreven met een stelsel indifferentiekrommen. Deze indifferentiekrommen geven goederencombinaties weer, die de consument eenzelfde nut opleveren. Een kromme, die verder van O ligt, correspondeert met een hoger nut. De krommen keren de bolle zijde naar de oorsprong op grond van de eerste wet van Gossen.
| |
3. Het streven naar maximale behoeftenbevrediging
De consumenten streven naar een zo groot mogelijke behoeftenbevrediging, d.w.z. naar een zo goed mogelijke voorziening van goederen. Zij willen dus een zo hoog mogelijk nut. Uitgedrukt in de grafische voorstelling van de vorige paragraaf betekent dit, dat de consument een indifferentiekromme wil bereiken, die zo ver mogelijk van O af ligt.
De economie is de wetenschap van de schaarste, d.i. van de spanning tussen behoeften en bevredigingsmiddelen. De schaarste van de goederen komt tot uitdrukking in het feit, dat er prijzen voor de goederen moeten worden betaald. Voor lucht behoeft geen prijs te worden betaald, omdat er voldoende van is t.o.v. de behoefte. De consument betaalt de aankoop van goederen uit zijn inkomen. Hieruit volgt, dat zijn streven naar maximale behoeftenbevrediging beperkt wordt door zijn inkomen en de prijzen van de beide goederen. Ons probleem luidt dus: welke goederencombinatie maximaliseert het nut van de consument gegeven zijn inkomen en de prijzen van de goederen?
| |
Conclusie
Het streven van de consument naar maximale behoeftenbevrediging wordt beperkt door zijn inkomen en de prijzen van de goederen.
| |
4. Het evenwicht van de consumptiehuishouding
Stel de prijs van appelen per kg p1 en die van peren per kg p2 en noem de hoeveelheid appelen y en de hoeveelheid peren x. Het
| |
| |
bedrag dat de consument aan appelen besteedt, is dan p1y en het bedrag dat hij aan peren besteedt, bedraagt p2x. Als het inkomen i volledig wordt verdeeld over appelen en peren, zal dus gelden:
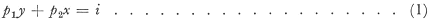
Bij meer goederen kan men een soortgelijke vergelijking opschrijven, doch eenvoudigheidshalve beperken wij ons tot de appelen en peren. Uit de vergelijking volgt, dat x/p1 appelen kunnen worden gekocht, als het gehele inkomen aan appelen wordt uitgegeven. Precies zo geldt, dat i/p2 peren kunnen worden gekocht, als i volledig hieraan wordt besteed. Hieruit blijkt al, dat (1) aangeeft welke combinaties van appelen en peren gezien prijzen en inkomen bereikbaar zijn. De beide uiterste gevallen zijn in figuur 7 A en B genoemd.
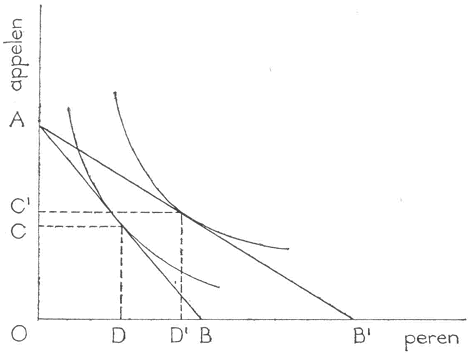
Fig. 7
Om alle tussenliggende gevallen te vinden moeten wij de betrekking tussen y en x opschrijven, want op de assen van figuur 7 staan immers y en x. Er volgt gemakkelijk:

| |
| |
Nu geldt voor de consumenten vaak, dat zij door meer te kopen geen kortingen kunnen bedingen. Dus of er nu 4 of 40 kg appelen wordt gekocht, er moet steeds bv. ƒ 1,- per kg worden betaald. Als dat zo is, zeggen we, dat de consument hoeveelheidsaanpasser is. De prijs is gegeven, hij kan alleen bepalen welk quantum hij zal kopen.
In het geval van hoeveelheidsaanpassing stelt (2) grafisch een rechte lijn voor. Als bv. de prijs per kg appelen ƒ 1,- is, die per peren ƒ 2,- en het inkomen bedraagt ƒ 100,- per week, komt er:
y = -2x + 100 . . . . . . . . . . . . . . . . . . (3)
Dit is een lineaire functie waarvan de hellingscoëfficiënt negatief is. Uitsluitend in het geval van hoeveelheidsaanpassing kunnen we de punten A en B dus door een rechte lijn verbinden. Op deze lijn liggen alle goederencombinaties die gegeven het inkomen en de prijzen nog net kunnen worden gekocht. Erboven liggen onbereikbare combinaties en wanneer een goederenpakket wordt gekocht dat beneden AB ligt, houdt de consument geld over.
Welke goederencombinatie zal de consument nu kopen? Die combinatie die, gegeven zijn preferentieschema, de prijzen en zijn inkomen, het hoogste nut oplevert. Derhalve moeten weer de indifferentiekrommen worden getekend. Het nut is nu maximaal als de consument de combinatie koopt waarbij de budgetlijn y = - 2x + 100 raakt aan een indifferentiekromme. Een hogere indifferentiekromme is immers niet te bereiken en een lagere is onverstandig, omdat het nut dan nog kan worden verhoogd.
De optimale goederencombinatie bij deze prijzen en dit inkomen bestaat voor deze consument dus uit OC appelen en OD peren.
| |
Conclusie
Het evenwicht van de consumptiehuishouding wordt gevonden door de hoogste indifferentiekromme op te zoeken die verenigbaar is met de budgetlijn. Bij het tekenen van de budgetlijn is aangenomen, dat de consument geen invloed op de prijzen kan uitoefenen. Hij is dan hoeveelheidsaanpasser.
| |
| |
| |
5. Prijsveranderingen
Laten wij nu eens aannemen, dat de groenteboeren de prijs van de peren op ƒ 1,50 stellen. De peren worden dus goedkoper. Hoe zal onze consument nu reageren?
De vergelijking van de budgetlijn wordt nu:
y = -1,5x + 100 . . . . . . . . . . . . . . . . . (3)
Het punt B verschuift op de horizontale as naar rechts. Dit is ook begrijpelijk, want als de consument nu zijn hele inkomen aan peren zou besteden, zou hij meer peren kunnen kopen. De hoeveelheid appelen die hij kan kopen, wanneer hij alles aan appelen besteedt, blijft echter gelijk.
De nieuwe budgetlijn is dus AB' en de nieuwe optimale combinatie wordt weer gevonden door de indifferentiekromme op te sporen die nog juist raakt aan AB'.
Terwijl alleen de perenprijs is verlaagd, valt het op dat door deze consument zowel meer appelen als meer peren worden gekocht. De perenprijs blijkt niet alleen de gevraagde hoeveelheid peren, maar ook de gevraagde hoeveelheid appelen te beïnvloeden. Wij zeggen, dat de vraag naar peren een functie is van de prijs van peren en de prijs van appelen. Precies zo geldt, dat de vraag naar appelen afhankelijk is van de appelenprijs en de perenprijs. Dit op het eerste gezicht merkwaardige resultaat is het gevolg van de omstandigheid, dat elke prijsverandering ook het reële inkomen van de consument verandert. Het reële inkomen geeft het goederenpakket aan, dat met het nominale inkomen kan worden gekocht. Als de prijs van scheermesjes daalt, is het niet alleen mogelijk meer scheermesjes te kopen, doch ontstaat er ook ruimte om meer andere artikelen te kopen.
Algemeen geldt dus: de vraag naar elk artikel is een functie van de prijzen van alle goederen.
| |
Conclusie
Uit de theorie van het consumentengedrag kan de belangrijke conclusie worden afgeleid, dat de vraag naar een artikel niet alleen afhankelijk is van de prijs van het betrokken goed, maar ook van de prijzen van alle andere goederen.
| |
| |
| |
6. Inkomensveranderingen
De optimale goederencombinatie verandert ook als het inkomen verandert. Als het inkomen tot ƒ 200,- per week stijgt, verschuift de budgetlijn evenwijdig met zichzelf naar boven. De nieuwe evenwichtssituatie kan dan weer op dezelfde manier worden bepaald als bij een prijsverandering.
De individuele vraag naar een consumptiegoed is dus niet alleen afhankelijk van alle prijzen, maar ook van het inkomen van de consument. Wij zeggen, dat de individuele vraagfunctie een functie is van alle prijzen en het inkomen. De individuele vraagfunctie is dus een ingewikkelde relatie en hier hebben we nu een duidelijk geval waarin het hanteren van de ceteris paribus conditie noodzakelijk is. Als men de vraag uitsluitend in afhankelijkheid van het inkomen bekijkt en dus de prijzen constant laat, wordt de grafische voorstelling van dat verband Engelkromme genoemd. Engel was een Duits statisticus uit de vorige eeuw. Bestudeert men het bedrag, dat aan het goed wordt besteed in afhankelijkheid van het inkomen, dan heeft men een micro-economische consumptiefunctie, die op één goed betrekking heeft. Een Engel- of verbruikskromme is in figuur 8 getekend, waarbij is aangenomen, dat naarmate het inkomen toeneemt ook het verbruik na een zekere drempel toeneemt, zij het op den duur minder dan evenredig.
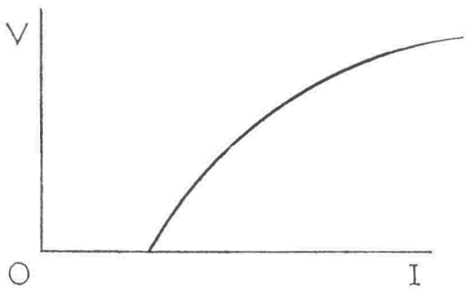
Fig. 8
De verbruikskromme kan dus verschuiven, omdat de prijzen van de goederen veranderen.
Een statistische methode om een indruk te krijgen van een verbruikskromme is het budgetonderzoek. Daarbij kan men natuurlijk niet wachten tot één consument achtereenvolgens ƒ 100, -, ƒ 200, -,
| |
| |
ƒ300,- enz. per week verdient, om zijn verbruik te bepalen bij deze uiteenlopende inkomens. Bij het budgetonderzoek gaat men van een aantal consumenten met verschillende inkomens na hoeveel zij bv. per jaar van een bepaald artikel gebruiken. Zo krijgt men dus ook een indruk van de verbruikskromme van het betrokken goed. Het budgetonderzoek is vooral van belang voor de berekening van het prijsindexcijfer van de kosten van levensonderhoud, omdat de bedragen die aan de diverse artikelen zijn besteed nu juist de gewichten zijn die voor die index van belang zijn. In Nederland zijn budgetonderzoekingen gehouden in 1951 en 1960.
Houdt men naast het inkomen ook alle andere prijzen constant, dan resulteert dus het verband tussen de vraag naar het goed en de prijs ervan. De individuele vraagfunctie in engere zin zullen wij voortaan de individuele vraagfunctie noemen, tenzij anders vermeld is.
De individuele vraagfunctie heeft meestal een dalend verloop; bij een hogere prijs hoort een lagere gevraagde hoeveelheid. Dit is in figuur 9 tot uitdrukking gebracht. Bij een prijs 2½ wordt 1 eenheid gevraagd, bij een prijs 1 worden 3 eenheden gevraagd.
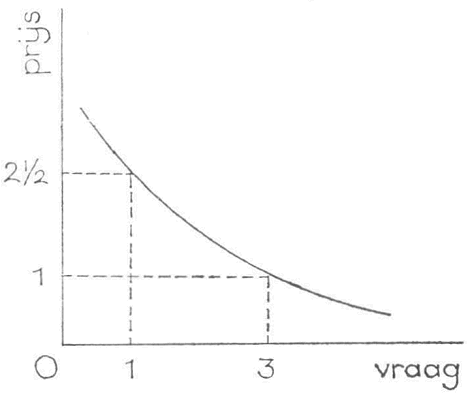
Fig. 9
| |
Conclusie
De individuele vraagfunctie in engere zin is een ceteris paribus vraagfunctie, want alle andere prijzen en het inkomen zijn constant gehouden. Dit moeten wij ons steeds voor ogen houden, als wij het navolgende lezen.
| |
| |
| |
7. De collectieve vraagfunctie
De collectieve vraagfunctie is de som van alle individuele vraagfuncties, dus de vraag van alle consumptiehuishoudingen tezamen. De collectieve vraagfunctie wordt gevonden door alle individuele vraagfuncties horizontaal op te tellen. Dit is hieronder voor twee consumenten gedaan.
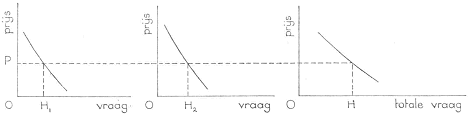
Fig. 10
De collectieve vraagfunctie geeft weer, welke hoeveelheden bij uiteenlopende prijzen zullen worden gevraagd. Daarbij zijn de prijzen van andere goederen en de inkomens van de consumenten constant gehouden.
De collectieve vraagfuncties zijn een noodzakelijke aanvulling op de macro-economische consumptiefunctie, omdat zij ons een inzicht geven in de samenstelling van het bestedingentotaal en in de factoren waardoor deze samenstelling kan veranderen. De macroeconomische consumptiefunctie geeft aan, welk totaal bedrag bij uiteenlopende hoogten van het nationale inkomen wordt besteed, zonder dat iets over de opbouw van dit bedrag wordt gezegd. Uit de analyse van het consumentengedrag blijkt, dat deze opbouw in het bizonder door de prijzen van de goederen wordt beheerst. Gegeven de preferenties van de consumenten leiden veranderingen in de prijsverhoudingen tot wijzigingen in de optimale goederenpakketten en daarmede in de struktuur van de consumptie.
Intussen mag niet worden vergeten, dat met de afleiding van de collectieve vraagfunctie voor een bepaald produkt uit de theorie van het consumentengedrag nog niet is aangegeven, welke prijs in feite zal ontstaan. Er is vastgesteld wat de consumenten bij uiteenlopende
| |
| |
prijzen zullen kopen. Slechts één van deze prijzen komt werkelijk tot stand. Hoe, zien wij in hoofdstuk IX.
| |
Conclusie
De collectieve vraagfunctie geeft ons een inzicht in de factoren die de vraag naar een goed bepalen. Daardoor krijgt ook de C uit de consumptiefunctie meer reliëf, want we zien nu, dat met name de opbouw van C wordt beheerst door de prijzen van de goederen.
| |
8. Slotopmerkingen
In dit hoofdstuk is de theorie van het consumentengedrag besproken zoals die na Pareto de gangbare is geworden. Het nut is, zoals na Pareto gebruikelijk is, rangschikbaar ondersteld en niet meetbaar. De eerste wet van Gossen bepaalt de vorm van de indifferentiekrommen. Gossen, die leefde in het midden van de 19de eeuw, was een voorloper van de grensnutschool in de economie. Deze school, die omstreeks 1870 is ontstaan en waartoe Menger, Jevons en Walras behoorden, heeft vooral de rol van de consument in het economisch proces geanalyseerd. Zoals wij nog zullen zien, was dit een reactie op de Klassieke School (± 1800), die speciaal aandacht aan de produktiekant heeft geschonken.
De grensnutschool kan nog nader worden onderverdeeld in de Oostenrijkse School, de School van Cambridge en de School van Lausanne. Tot de Oostenrijkse School worden, naast Menger, Von Wieser en Von Böhm Bawerk gerekend. Een van de latere aanhangers is Schumpeter. De grondlegger van de School van Cambridge is Marshall, die in tegenstelling tot Jevons meer aansluiting zocht bij de Engelse Klassieken, zoals Smith, Ricardo en Mill. Walras werd het hoofd van de School van Lausanne, waartoe ook Pareto kan worden gerekend. Walras en zijn volgelingen hebben veelvuldig gebruik gemaakt van wiskundige methoden.
Met behulp van de budgetlijn is het evenwicht van de consumptiehuishouding vastgesteld. Door de prijzen en het inkomen te veranderen kregen we een inzicht in de individuele vraagfunctie. Uit de individuele vraagfuncties hebben wij tenslotte de collectieve vraagfuncties afgeleid.
| |
| |
| |
9. Vragen
| 1. | Wat is het verschil tussen de theorie van het consumentengedrag voor en na Pareto? |
| |
| 2. | Waarom is de budgetlijn recht? |
| |
| 3. | Teken een stel indifferentiekrommen. De prijs van appelen is ƒ 3,- per kg, die van peren ƒ 2,- en het inkomen is ƒ 50,- per week. Bepaal de optimale combinatie van appelen en peren. |
| |
| 4. | Hoe wordt deze combinatie in de figuur beïnvloed door de appelenprijs twee keer zo hoog te nemen? |
| |
| 5. | Wat gebeurt er als het inkomen twee keer zo hoog wordt? |
| |
| 6. | Waardoor kan de collectieve vraagfunctie verschuiven? |
|
|