De kern van de economie

[p. 21]

III. De hoogte van het nationale geldinkomen

1. Het probleem

Door de overwegend inductieve beschrijving van het macro-economische gebeuren in een volkshuishouding hebben wij een indruk gekregen van de betrekkingen tussen gezinnen en bedrijven. De bedrijven kunnen opgevat worden als de cellen waarin de bevredigingsmiddelen worden voortgebracht, terwijl in de gezinnen de bevredigingsmiddelen worden geconsumeerd. Gebleken is, dat er een nationaal geldinkomen ontstaat, dat gelijk is aan de waarde van het netto nationale produkt. In ons rekenvoorbeeld was Y gelijk aan 22. Maar, waarom is Y niet gelijk aan 20 of 30? De vraag komt op, waarvan de hoogte van Y afhangt. Het antwoord op deze vraag is van grote maatschappelijke betekenis. Wij hebben gezien, dat het nationale geldinkomen gelijk is aan de waarde van het netto nationale produkt. Dit betekent dus dat een laag nationaal geldinkomen hetzelfde is als een geringe omvang van de nationale produktie. En nu spreekt het vanzelf, dat een lage produktie met een geringer aantal arbeiders kan worden voortgebracht dan een grote produktie-omvang. In wezen is de vraag naar de hoogte van het nationale geldinkomen dezelfde als de vraag naar de factoren die de werkgelegenheid bepalen. Ook uit de statistieken kan men opmaken, dat de totale produktie en de werkgelegenheid dezelfde fluctuaties doormaken.

Het nationale inkomen wordt gevormd door de produktie. Als we dus kunnen bepalen waar het nationale produkt van afhangt, zijn de factoren die de vorming van het nationale inkomen bepalen ook bekend. Nu valt de waarde van het netto nationale produkt uiteen in de waarde van de consumptiegoederen en de waarde van de nettoinvesteringen. Er geldt immers W = C + I. Een analyse van de factoren die W (en dus Y) bepalen dwingt ons te zoeken naar de achtergrond van C en I.

Conclusie

Een onderzoek naar de factoren, die de hoogte van het nationale inkomen en de nationale produktie bepalen is van groot praktisch

[p. 22]

belang, gezien het probleem van de werkgelegenheid. Een dergelijk onderzoek bestaat uit een nadere bespreking van C en I.

2. De macro-economische consumptiefunctie

Wij hebben gezien, dat de consumenten een bepaald deel van hun totale inkomen aan consumptie besteden. In ons voorbeeld op pag. 14 was dat 10/11. Het ligt voor de hand te veronderstellen, dat het bedrag, door de consumenten aan consumptiegoederen uitgegeven, verband houdt met hun totale inkomen. Uit statistische onderzoekingen blijkt dit ook inderdaad het geval te zijn. Als het nationale inkomen toeneemt stijgt ook het bedrag dat aan consumptie wordt uitgegeven. Daarbij heeft men ook geconstateerd, dat de consumptie niet zo sterk stijgt als het nationale inkomen. Eenvoudigheidshalve zullen wij aannemen dat C rechtevenredig is met Y. In het onderstaande staatje is een dergelijk geval weergegeven. De grootheden zijn in mld. guldens uitgedrukt.

Verband tussen C en Y
C	Y
16	24
20	30
24	36
30	45
40	60

Aangenomen is, dat C = ⅔ Y. Dit betekent, dat van elke stijging van het inkomen steeds een gedeelte ⅔ consumptief zal worden besteed.

Het verband tussen C en Y heet de macro-economische consumptiefunctie. Het getal ⅔ wordt de marginale consumptiequote genoemd. De marginale consumptiequote geeft de verhouding aan van de extra consumptie en het extra inkomen, dat de consumptiestijging veroorzaakt. Deze breuk is steeds kleiner dan 1, omdat de consumptietoename hoogstens gelijk is aan de stijging van het nationale inkomen.

[p. 23]

De consumptiefunctie kan ook grafisch tot uitdrukking worden gebracht. Daartoe is in figuur 1 horizontaal het nationale geldinkomen Y en verticaal de consumptie C afgebeeld. De functie C = ⅔ Y stelt een rechte lijn door de oorsprong voor.

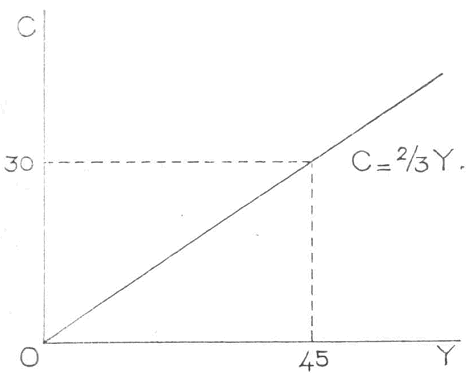
Fig. 1

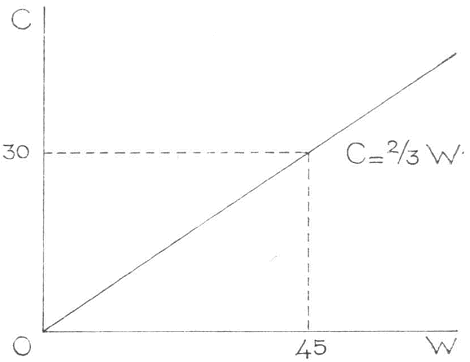
Fig. 2

Daar Y steeds gelijk is aan W kan men ook zeggen, dat C een functie is van W. M.a.w. het bedrag dat de gezinnen aan consumptie besteden, is afhankelijk van de waarde van het netto nationale produkt. In figuur 2 is daarom C als functie van W getekend. Het enige verschil met figuur 1 is, dat nu W i.p.v. Y op de horizontale as staat afgebeeld.

De vergelijking C = ⅔ Y, resp. C = ⅔ W moet goed worden onderscheiden van de definitievergelijkingen, die in het vorige hoofdstuk ter sprake kwamen. De definitievergelijkingen zeggen op zichzelf niets; zij drukken slechts identiteiten uit. Uit een gelijkheid van het type Y = C + S kan uiteraard niets omtrent de hoogte van Y worden afgeleid. Er wordt slechts aangegeven, dat, welke Y er ook ontstaat, deze steeds gelijk is aan de som van consumptie en besparingen. De vergelijking voor de consumptiefunctie daarentegen drukt een bepaald gedrag uit van alle consumenten tezamen. Men spreekt daarom ook wel van een gedragsvergelijking. Juist de gedragsvergelijkingen zijn de eigenlijke bouwstenen van een theorie.

Nu behoeft het niet zo te zijn, dat het gedrag van alle consumenten tezamen precies door zo'n mooi lijntje zoals in figuur 2 is getekend, wordt beschreven. Het menselijk gedrag vertoont meestal een grilliger

[p. 24]

baan. Maar ook wanneer de baan ingewikkelder is, blijft de grondgedachte dezelfde: er is een samenhang tussen het totale bedrag dat aan consumptie wordt uitgegeven en de waarde van het nationale geldinkomen. Als we in gedachten houden, dat dit verband in de werkelijkheid ingewikkelder kan zijn, is er niets tegen ons de macroeconomische consumptiefunctie eenvoudigheidshalve als een rechte lijn door de oorsprong voor te stellen.

Conclusie

De macro-economische consumptiefunctie is een gedragsvergelijking die ons leert van welke grootheid de totale consumptie in een volkshuishouding afhangt. Omdat Y en W identiek zijn kan men C zowel als functie van Y als van W opvatten.

3. De netto-investeringen

De gezinnen oefenen een vraag naar consumptiegoederen uit, de bedrijven vragen kapitaalgoederen en houden bepaalde voorraden aan. Over C beslissen de consumenten, over I zijn de producenten de baas. Eenvoudigheidshalve zullen we nu aannemen, dat de bedrijven hebben besloten een bedrag van 20 te investeren, geheel onafhankelijk van de hoogte van het nationale produkt. Onafhankelijk van de hoogte van W stellen de producenten zich dus voor de voorraden kapitaalgoederen, consumptiegoederen en halffabrikaten aan het einde van de periode met 20 te laten stijgen. Of W nu 100 of 200 zal zijn, steeds is I = 20. We zeggen, dat de investeringen autonoom, d.i. onafhankelijk van de hoogte van het nationale inkomen zijn. Dit gedrag van de producenten kan eveneens grafisch worden weergegeven, zoals in figuur 3 is gedaan. De investeringsfunctie is een rechte evenwijdig aan de horizontale as, omdat I ten opzichte van W steeds constant nl. 20 is.

Fig. 3

[p. 25]

Conclusie

De investeringsfunctie is een gedragsvergelijking, die de vraag van de bedrijven naar investeringen beschrijft. Als eerste benadering kan I onafhankelijk van W worden beschouwd.

4. De totale effectieve vraag

De totale effectieve vraag is de vraag van de gezinnen naar consumptiegoederen vermeerderd met de investeringsvraag van de bedrijven. Steeds is dus E.V. = C + I. Voor elke waarde van W kunnen wij de effectieve vraag uitrekenen. Dit is in onderstaande tabel gedemonstreerd voor enkele waarden van W. Als W = 12 zal C (= ⅔ W) gelijk aan 8 moeten zijn. Daar I steeds 20 is, is in die situatie de effectieve vraag 8 + 20 = 28. Nu is dus E.V. groter dan W. De effectieve vraag overtreft de waarde van het netto nationale produkt. Dit geval doet zich ook voor wanneer W 24, 36 en 48 is.

Berekening van de effectieve vraag (e.v.)
W	C = ⅔ W	I = 20	E.V.
12	8	20	28
24	16	20	36
36	24	20	44
48	32	20	52
60	40	20	60
72	48	20	68

Voor de eerste vier waarden van W is de effectieve vraag derhalve groter dan de waarde van de netto nationale produktie. Deze situaties zijn niet van blijvende aard; het zijn geen evenwichtssituaties. De producenten worden immers door de grote vraag gedwongen minder voorraden aan te houden dan zij van plan waren. Hun investeringen dreigen daardoor beneden de 20 te komen. Op deze verschijnselen zullen zij reageren door hun produktie uit te breiden. Tot hoever? Wanneer komt W tot rust? Wanneer de netto nationale produktie precies gelijk is aan de effectieve vraag. De bedrijven investeren dan

[p. 26]

precies wat zij van plan waren en de gezinnen kopen precies datgene wat bij deze evenwichtsproduktie is geproduceerd aan consumptiegoederen. In het voorbeeld wordt de evenwichtstoestand bereikt voor W = 60. Bij die waarde van W komen de wensen van producenten en consumenten uit.

Als W = 72 schiet de effectieve vraag te kort om deze produktie op te nemen. Bij een netto nationaal produkt van 72 wordt immers slechts een vraag van 68 uitgeoefend. In die situatie zouden de voorraden bij de ondernemers dus tegen hun zin oplopen. Zo gauw zij dit zien gebeuren zullen zij hun produktie aanpassen, tot deze gelijk is aan de effectieve vraag.

Wij zien, dat de hoogte van het netto nationale produkt bepaald wordt door de effectieve vraag naar consumptie, kapitaalgoederen en halffabrikaten. De totstandkoming van de evenwichtsproduktie kan ook grafisch worden aangegeven. Daartoe zijn in figuur 4 de consumptiefunctie, de investeringsfunctie en de identiteit W = C + I getekend. Voor het evenwicht moet er immers een gelijkheid bestaan tussen de waarde van het netto nationale produkt en de effectieve vraag. Ons getallenvoorbeeld leerde, dat de bedoelingen van consumenten en producenten alleen maar uitkomen als W = E.V. = C + I = 60.

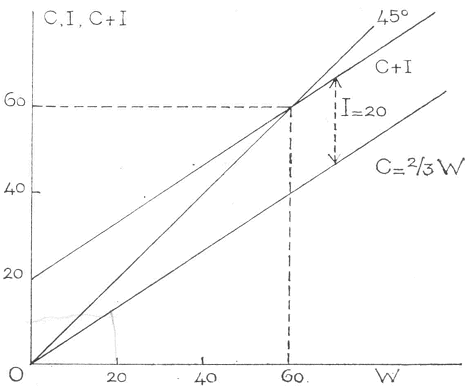
Fig. 4

[p. 27]

Het evenwicht van de netto nationale produktie W wordt gevonden door het snijpunt te bepalen van de lijn C + I met de 45^o-lijn W = C + I. De lijn C + I, die een functie is van W krijgen we door bij C = ⅔ W steeds een bedrag 20 op te tellen. De lijn begint dus bij het getal 20 op de verticale as, omdat C = 0 als W = 0. Zo kan men elk punt van de lijn C + I vinden. Dat de vergelijking W = C + I een 45^o-lijn door O is, volgt uit het feit dat op de assen W en C + I staan afgebeeld. Als op dezelfde assen resp. x en y staat, is de vergelijking van de 45^o-lijn immers x = y.

Er ontstaat dus een netto nationaal produkt van 60, dat voor een bedrag 40 uit consumptiegoederen en voor een bedrag 20 uit investeringen bestaat. Aan de gezinnen is dus ook een geldinkomen Y ten bedrage van 60 uitgekeerd. Hiervan is 40 besteed voor de aankoop van de consumptiegoederen. De rest 20 is dus bespaard. Hieruit volgt, dat het evenwichtsinkomen zo hoog wordt, dat daaruit precies een bedrag wordt bespaard gelijk aan de investeringen van de bedrijven: S = I = 20. Afwijkingen van het evenwicht, die aan de kant van de produktie tot uiting kwamen in ongewilde voorraadmutaties, blijken wat de bestedingen betreft uit een verschil tussen gewenste besparingen en gewenste investeringen. Als bv. een nationaal produkt van 72 zou ontstaan zijn de besparingen 72 - 48 = 24. De investeringen zijn steeds 20 en in dit geval zijn de gewenste besparingen dus groter dan de gewenste investeringen, hetgeen inhoudt dat de nationale produktie te groot is ten opzichte van de effectieve vraag. Er is rust wanneer de gewenste besparingen gelijk zijn aan de gewenste investeringen.

Conclusie

De hoogte van het netto nationale produkt en daarmede van het nationale geldinkomen wordt bepaald door de effectieve vraag, d.w.z. door de som van consumptieve en investeringsvraag. Dat dit inderdaad zo is kunnen we echter pas goed inzien, als is aangetoond dat een ander nationaal geldinkomen ontstaat, indien de consumptiefunctie en de investeringsfunctie op een ander niveau liggen.

[p. 28]

5. Veranderingen in consumptie - en investeringsneiging

Laten we nu eens aannemen, dat C niet gelijk is aan ⅔ Y, maar aan ½ Y. M.a.w. de marginale consumptiequote is kleiner geworden. We kunnen zeggen, dat de spaarneiging van de bevolking is toegenomen, want bij elke hoogte van het nationale inkomen wordt nu 50 % gespaard tegenover vroeger 33 %.

Veronderstellen we nu, dat I steeds gelijk is aan 15. Hoe hoog zal nu het evenwichtsinkomen worden? We weten C = ½ Y, dus C = ½ W, I = 15 en W = C + I. Hieruit kan men gemakkelijk afleiden, dat de evenwichtswaarde nu gelijk is aan 30; Y en W zijn dus tot de helft gedaald. De daling van de effectieve vraag, de toename van de spaarneiging heeft dus tot gevolg dat het nationale geldinkomen zal dalen.

In figuur 5 is ook deze situatie getekend. Het is van belang deze figuur goed met figuur 4 te vergelijken.

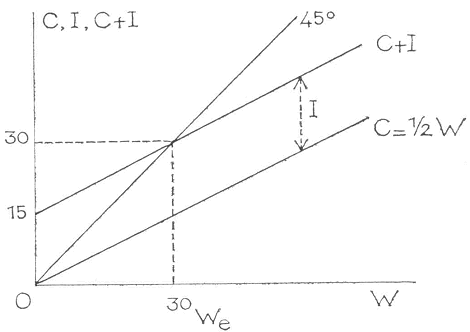
Fig. 5

Conclusie

Als de effectieve vraag van gezinnen en bedrijven naar goederen afneemt daalt het nationale geldinkomen. Als deze effectieve vraag toeneemt stijgt het nationale geldinkomen.

6. De werkgelegenheid

Uit het voorgaande volgt, dat de hoogte van het netto nationale produkt afhangt van de effectieve vraag. Als de gezinnen ineens bij

[p. 29]

elk inkomen meer willen sparen, d.w.z. als hun spaarneiging toeneemt, daalt C en daarmede de effectieve vraag, zodat ook de produktie daalt, omdat de ondernemers deze afstemmen op de effectieve vraag. Dit betekent, dat arbeiders die tot voor kort aan het werk waren, zullen worden ontslagen en dat er machines stil komen te staan. Een toestand waarin grote werkloosheid heerst en de machines niet draaien heet een depressie. Een depressie kan worden verklaard uit het tekortschieten van de effectieve vraag.

Stel dat om de één of andere reden de effectieve vraag weer wordt gestimuleerd. Zal W dan onbeperkt omhoog kunnen gaan? Dit is niet het geval, omdat dan de omvang van de beroepsbevolking als knelpunt fungeert. De waarde W van het netto nationale produkt kan worden opgevat als het produkt van het prijspeil P en de physieke omvang T van de consumptiegoederen en de voorraadverandering. Deze waarde van T kan niet meer stijgen, wanneer het punt van volledige werkgelegenheid is bereikt. De effectieve vraag doet T allen maar toenemen, indien we ons in de fase bevinden waarin T nog kan toenemen, nl. wanneer er nog werkloosheid bestaat. Voor het punt van volledige werkgelegenheid doet een toename van de effectieve vraag, de produktie T en daarmede de waarde W van deze produktie stijgen. Hierbij kan worden aangenomen, dat het prijspeil P constant blijft. Het prijspeil P is een gemiddelde van de prijzen van de goederen. Er is geen reden om aan te nemen, dat de goederen duurder in prijs zullen worden, omdat het aanbod van goederen zich zonder enige moeite kan aanpassen aan de extra vraag.

Dit wordt anders, indien alle arbeiders aan het werk zijn. Dan leidt een vergroting van de effectieve vraag tot spanningen, omdat de bedrijven niet nog meer kunnen produceren. Zij zitten aan de grens van de produktie-capaciteit. In die situatie kan T niet meer stijgen. De toegenomen schaarste van de goederen komt dan tot uitdrukking in prijsstijging. Voorbij het punt van volledige werkgelegenheid leidt een toename van de effectieve vraag uitsluitend tot een hoger prijspeil.

Conclusie

De waarde van het netto nationale produkt W is gelijk aan P.T. De hoogte van dit nationale produkt en daarmede van het nationale geldinkomen Y wordt steeds bepaald door de effectieve vraag.

[p. 30]

Wanneer nog niet alle arbeiders aan de slag zijn, leidt een verandering van de effectieve vraag tot een wijziging in T bij gelijkblijvende P. Zijn alle arbeiders aan het werk, dan kan T niet meer stijgen en leidt een toename van de effectieve vraag tot een stijging van P.

7. Het prijspeil

De vaststelling van het prijspeil is een statistisch vraagstuk, waarvan enige kennis noodzakelijk is. Een verandering in het prijsniveau wordt tot uitdrukking gebracht met behulp van zg. indexcijfers.

Laten we gemakshalve eens aannemen, dat er slechts één consumptiegoed en één kapitaalgoed wordt gemaakt. Als consumptiegoed nemen wij tarwebrood en als kapitaalgoed deegmachines. In de uitgangssituatie - de basisperiode - is de prijs van tarwebrood 20 cent per brood en de prijs van een deegmachine ƒ 100.000.-. Stel dat in de beschouwde periode de broodprijs tot 25 cent is gestegen en dat de deegmachine nu ƒ 150.000 kost. Wij zijn nu geïntereseerd in de gemiddelde prijsstijging. Daartoe berekenen we eerst zg. partiële prijsindexcijfers. In de uitgangssituatie worden de prijzen op 100 gesteld en we gaan na hoe hoog de prijzen in de beschouwde periode zijn t.o.v. de basisperiode. De partiële indices zijn dus 100 - 125 en 100 - 150.

Men is nu geneigd het prijspeil in de beschouwde periode te stellen op



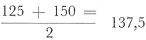
. Dit is echter niet juist, omdat zodoende geen rekening wordt gehouden met de relatieve betekenis, die deegmachines en broden in onze volkshuishouding hebben. Zo is het denkbaar, dat in de basisperiode slechts 2 deegmachines zijn gemaakt, terwijl 3 miljoen broden zijn verkocht. Dit betekent, dat de omzet in deegmachines ƒ 200.000 was en die in broden ƒ 600.000. M.a.w. aan de prijsstijging van de broden moet een belangrijker gewicht worden toegekend dan aan de prijsstijging van de deegmachines. We zeggen, dat de partiële prijsindexcijfers moeten worden gewogen met de omzetten uit de basisperiode. Het samengestelde gewogen prijsindexcijfers wordt dan

[p. 31]

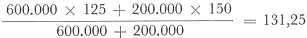
Het prijspeil is derhalve met ruim 31 % gestegen, omdat de index van het algemeen prijsniveau ten opzichte van de basisperiode 31,25 punten is toegenomen.

Het berekenen van indexcijfers is één van de belangrijkste activiteiten van het C.B.S. Zo publiceert men maandelijks de index van de kosten van levensonderhoud. Dit indexcijfer is een gewogen gemiddelde van de partiële prijsindexcijfers van consumptiegoederen die door een bepaalde sociale laag (bv. de handarbeiders) worden gekocht. Er wordt eveneens gewogen met de bedragen die deze mensen in de basisperiode aan de diverse artikelen besteden. Deze omzetten geven immers aan hoe belangrijk een bepaalde prijsontwikkeling is. Stel bv. dat de partiële prijsindex voor kleding met 200 punten oploopt. Speelt dat een belangrijke rol in de samengestelde prijsindex, die een gemiddelde is van alle partiële indices? Dat hangt ervan af. Als de gezinnen waar het om gaat naaktlopers zijn, laat het ze letterlijk en figuurlijk koud of deze index zo sterk gestegen is. Maar als zij een groot deel van hun inkomen aan kleding besteden, speelt de sterke stijging van de kledingprijs een belangrijke rol.

Conclusie

Het algemeen prijsniveau is een gewogen gemiddelde van alle goederenprijzen, dat statistisch met behulp van indexcijfers kan worden vastgesteld. Daarbij spelen de gewichten een belangrijke rol. De index van de kosten van levensonderhoud wordt maandelijks door het C.B.S. gepubliceerd. Het verloop van deze index kunnen we maandelijks in de krant volgen.

8. Keynes

Een toestand van grote werkloosheid heeft zich voor de tweede wereldoorlog in de jaren dertig vrijwel over de gehele wereld voorgedaan. Juist in die tijd is de theorie ontstaan, waarvan hierboven de kern is aangegeven. De theorie is opgesteld door de grote Engelse econoom John Maynard Keynes (1884-1946).

In 1936 verscheen Keynes' boek ‘The General Theory of Employment, Interest and Money’, waarin hij betoogde, dat de depressie waarin de wereld zich bevond moest worden verklaard uit het tekort-schieten van de totale effectieve vraag. Naar zijn inzicht is de consump-

[p. 32]

tiefunctie tamelijk stabiel, omdat consumptiegewoonten slechts langzaam veranderen en moeilijk te beïnvloeden zijn. De ondernemers hebben in een dergelijke situatie geen enkel belang bij investeringen. De ondernemers zijn immers uit op het behalen van winst en die is alleen maar te verkrijgen, indien een sterke vraag naar consumptiegoederen het aantrekkelijk maakt produktie-omwegen in te slaan. Volgens Keynes kan de volkshuishouding dan ook alleen weer op gang worden gebracht doordat de overheid de effectieve vraag stimuleert, bv. door zelf investeringen ter hand te nemen.

De theorie van Keynes is in grote trekken thans algemeen aanvaard en speelt een dermate grote rol, dat wij er nog uitvoerig aandacht aan zullen schenken.

Conclusie

De grote crisis van de jaren dertig is voor één van de grootste economen van onze tijd aanleiding geweest grondig na te denken over de factoren die de hoogte van het nationale inkomen, de nationale produktie en de werkgelegenheid bepalen. Keynes' conclusie, dat alles draait om de effectieve vraag van gezinnen en bedrijven, is een belangrijk uitgangspunt voor de verdere theorie en een aanknopingspunt voor de bestrijding van het kwaad der ernstige werkloosheid.

9. Slotopmerkingen

In dit hoofdstuk is aangetoond, dat de waarde van het nationale produkt bepaald wordt door de effectieve vraag. Deze effectieve vraag bestaat uit de vraag van de consumenten naar consumptiegoederen en uit de investeringsvraag van de producenten. De netto nationale produktie is alleen maar in rust, indien een zodanige W ontstaat, dat de investeringen van de bedrijven gelijk zijn aan de gewenste investeringen. Onverwachte wijzigingen van de voorraden treden dan niet op. Uit het evenwichtsinkomen dat bij deze situatie hoort, wordt door de gezinnen een bedrag S gespaard, dat precies gelijk is aan de investeringen I van de bedrijven. Boven het niveau van volledige werkgelegenheid komt een toename van de effectieve vraag tot uiting in een stijging van P.

[p. 33]

Als de consumptiefunctie en/of de investeringsfunctie verschuift, komt een ander evenwichtsinkomen tot stand. Daar bij elk niveau van de produktie een bepaald werkgelegenheidsniveau behoort, betekent een daling van de produktie eveneens de werkloosheid van een aantal werknemers. Voor Keynes was dit aanleiding te analyseren waarvan veranderingen in produktie, inkomen en werkgelegenheid afhangen.

10. Vragen

1.	Wie was Keynes?
2.	Wat is een depressie?
3.	a. Bereken het evenwichtsinkomen, indien de consumptiefunctie luidt C = 3/4 Y en de autonome investeringen 50 bedragen. b. Welk bedrag wordt uit het evenwichtsinkomen bespaard? c. Geef ook een grafische afleiding van het evenwicht.
4.	Dezelfde vragen indien C = ⅓ Y + 20 en I = 10. Deze consumptiefunctie is iets ingewikkelder dan de in dit hoofdstuk behandelde. Nu wordt immers aangenomen, dat de consumenten ook wanneer het nationale inkomen nihil is, een bedrag van 20 consumptief besteden, bv. door ontsparing.
5.	Dezelfde vragen indien C = ⅔ Y + 20 en er door de ondernemers niet wordt geïnvesteerd.
6.	Hoe hoog is deze maand de index van de kosten van levensonderhoud? Is deze gestegen of gedaald? Hoe wordt een dergelijke index berekend?