De stekelbaars

[p. 70]

5. Een zwemmende chronometer

Toen ik in april van het jaar 1965 voor het eerst het doorkruipgedrag van de mannelijke stekelbaars waarnam, kon ik onmogelijk voorzien dat dat gedrag, in al zijn facetten, mij de eerstvolgende twaalf jaar zou gaan bezighouden en het onderwerp zou worden van mijn proefschrift. Maar al na twee dagen in april vond ik datgene wat zich voor mijn ogen afspeelde zo fascinerend dat ik toen al zeker wist dat ik daaraan, voorzover dat mogelijk zou zijn, verder wilde werken.

Tijdens de derdejaarscursus ethologie hadden Inge, het meisje waarmee ik samenwerkte en ik, vier aquaria tot onze beschikking. In ieder aquarium huisde een eenzame man die in het bezit was van een leeg nest, een man, kortom, in seksuele fase. Even voor negen uur 's morgens namen wij plaats voor het aquarium en daarna observeerden en protocolleerden wij al het gedrag van één van de vier mannen. Al spoedig ontdekten wij dat één van de mannetjes elke morgen om negen uur precies door zijn nest kroop (afb. 44). Om tien uur ging hij opnieuw door zijn nest, om elf uur eveneens, om twaalf uur, om één uur enzovoort, de hele dag lang. Het mannetje kroop steeds door na precies 60 minuten sinds de vorige doorkruip al was er een enkele keer wel eens sprake van dat hij een halve minuut te vroeg of te laat was. Vanwaar die verwonderlijk starre regelmaat in het gedrag, die wekkerachtige ritmiek? Zwom daar in werkelijkheid een chronometer vermomd als stekelbaars? Ook onze andere drie mannen kropen zeer regelmatig door, zij het niet zo precies op tijd als ons zwemmende klokje dat wij de naam Karel hadden gegeven. Toch was ook bij die andere drie mannen sprake van grote regelmaat al konden de intervallen tussen twee doorkruipen dan wel eens drie tot vier minuten van elkaar verschillen. Ons zwemmende klokje Karel bleef evenwel met een uiterste regelmaat doorkruipen, alle dagen dat de cursus ethologie duurde, vier weken lang. En zelfs daarna placht hij, als ik door een ontluikend heimwee gedreven, even voor negen uur 's morgens stil naar binnen sloop op die Grote Zaal met de groen schemerende bakken, om negen uur precies door te kruipen alsof hij van buiten het sein kreeg dat de torenklok luidde of dat luiden zelf kon horen.

Niet alleen echter het doorkruipgedrag, ook het andere

[p. 71]

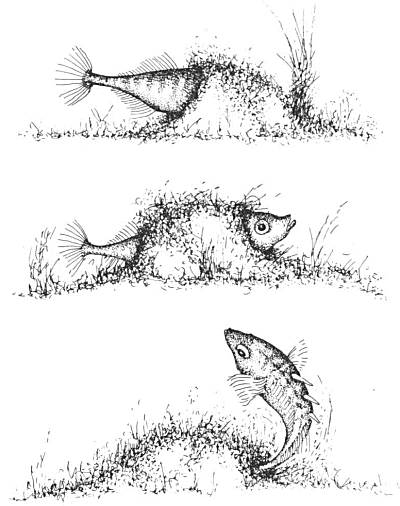
Afb. 44. Doorkruipen

gedrag tussen twee doorkruipen in vertoonde regelmatigheden. Vlak na het doorkruipen stampt de stekelbaars, zoals al eerder is verteld, het opgebolde nest in elkaar, hij waaiert dan in het geheel niet. Naarmate de tijd verstrijkt en het moment nadert waarop de te voorspellen volgende doorkruip weer zal plaatsvinden, neemt het waaieren toe. In de minuut vóór doorkruipen wordt gewoonlijk het meest gewaaierd. De toename van waaieren is zowel een gevolg van de toename van het aantal waaiers per minuut als van de toename van de duur van elke waaier afzonderlijk.

Na doorkruipen zie je zelden of nooit boren; pas kort voordat de volgende doorkruip komt, treedt boren op. Heel diep boren is vaak een aanwijzing dat het doorkruipen niet lang meer op zich zal laten wachten. Direct na doorkruipen patrouilleert de mannelijke stekelbaars veelal boven in het aquarium en voert hij vacuüm-zigzaggen uit alsof hij een voor de toeschouwer onzichtbaar wijfje ziet. De vacuüm-zigzaggen kunnen gericht zijn op slakjes, op een luchtbelletje of zelfs op een bewegend blad van een waterplant. Maar niet zelden zigzagt de mannelijke stekelbaars

[p. 72]

zonder zich te richten op een object. Het vacuüm-zigzaggen wordt gaandeweg minder naarmate het doorkruipen langer geleden is. Zo zijn cyclische veranderingen in waaieren, boren en vacuüm-zigzaggen nauw verbonden met de ritmiek van het doorkruipen. Alleen het plakken schijnt min of meer los te staan van de doorkruipritmiek. De mannelijke stekelbaars plakt met onregelmatige tussenpozen en we hebben geen verband kunnen ontdekken tussen de onregelmatige plakfrequentie en het zo stipt op tijd plaatsvindende doorkruipen.

Vanwaar, nogmaals, die wonderlijke ritmiek? Bij een dergelijke ritmiek zijn er altijd twee mogelijkheden. Of er is in de buitenwereld een prikkel aanwezig die met regelmatige tussenpozen weerkeert en waarop het dier reageert (zoals het opgaan en ondergaan van de zon die bij veel organismen een slaap-waak ritmiek induceert, zij het dat die ritmiek waarschijnlijk ook intern bepaald wordt) of in het dier zelf is een mechanisme voorhanden dat deze regelmatigheid produceert. Een combinatie van beide mogelijkheden is ook denkbaar. Bij ons zwemmende klokje dat zo stipt om het uur doorkroop zou het in principe denkbaar hebben kunnen zijn dat het slaan van de torenklok, hoorbaar in het laboratorium, het sein voor de stekelbaars was: nu moet ik doorkruipen. Maar aangezien andere dieren ook regelmatig, maar niet met tussenpozen van precies een uur, doorkropen kan het slaan van de klok de ritmiek zeker niet verklaren. In de buitenwereld van de stekelbaars, het aquarium en alles wat hij met zijn zo zeldzaam goede ogen buiten zijn aquarium ziet gebeuren, hebben wij geen enkele prikkel kunnen ontdekken die een dergelijke regelmaat zou kunnen veroorzaken. Ook onze eigen aanwezigheid kan de ritmiek niet veroorzaken want als wij de doorkruipen mechanisch registreren (kan met buisje over de uitgang van het nest waarin een fotocel zit die, als de stekelbaars na een doorkruip door het buisje gaat, het passeren van het visje registreert) vindt het net zo regelmatig plaats.

Een rijp vrouwtje

Toch is er één prikkel uit de buitenwereld die een ingrijpende invloed heeft op de ritmiek van het doorkruipgedrag. Die prikkel is: de aanblik van een kuitrijp vrouwtje. Zodra je in een glazen buis (om naar het nest volgen te verhinderen) een kuitrijp vrouwtje aanbiedt aan een mannelijke ste-

[p. 73]

kelbaars in seksuele fase, is er een vrij grote kans dat hij zal doorkruipen. Haal je nu dat vrouwtje dadelijk na de doorkruip weg, dan zal de volgende doorkruip veel eerder plaatsvinden dan je op grond van vroegere waarnemingen van de lengte van het doorkruipinterval zou verwachten. Ook de daaropvolgende doorkruip vindt eerder plaats dan verwacht; pas na een reeks doorkruipen (dus na enkele uren) is de oude toestand hersteld en gaat de stekelbaars weer regelmatig doorkruipen in zijn oude ritme. Als je de intervallen tussen de opeenvolgende doorkruipen na het aanbieden van een vrouwtje en weer weghalen van het vrouwtje goed bekijkt, kom je tot een merkwaardige ontdekking. Zo vonden we bij een bepaalde stekelbaars dat direct na aanbieden van een vrouwtje werd doorgekropen, daarna weer na 32,88 minuten (de seconden zijn hier omgerekend naar 100 in een minuut), waarna na 41,63 minuten en daarna na 53,02 minuten. Dat laatste getal, die 53,02 minuten, kun je nu al voorspellen uit die eerste twee getallen want 41,63²:32,88= 52,69, een getal dat maar weinig verschilt van 53,02. Hoe komt het nu dat je in staat bent van dat derde doorkruipinterval de lengte van te voren te berekenen? En het geldt niet alleen voor het derde, maar ook voor het vierde, vijfde enzovoort interval. Het vierde interval duurt namelijk 53,02² : 41,63 = 66,80 minuten. In werkelijkheid duurde dat vierde interval 67 min.

Dit alles betekent dat er in deze getallen sprake is van een voorspelbare geometrische progressie. Weet je de eerste twee intervallen tussen doorkruipen dan kun je daaruit alle volgende doorkruipintervallen betekenen. Dat is bepaald aardig: het betekent dat je ruim van te voren en haast op de minuut af kunt voorspellen wat het visje zal gaan doen. Neem het dier dat een eerste interval had van 31,30 minuten, een tweede van 78,55 minuten. Daaruit kun je berekenen dat het derde interval 197,12 minuten moet gaan duren. Je kunt dus ruim drie uur van te voren voorspellen wat een dier op een bepaald moment zal gaan doen. In werkelijkheid kwam die vierde doorkruip na precies 200 minuten.

Hebben we hiermee nu een sleutel in handen voor het begrijpen van die regelmaat? In ieder geval kunnen we een soort model ontwerpen en dat heeft Nelson, de eerste die, samen met Sevenster, deze geometrische progressie na een kortdurende wijfjes-stimulus waarnam, dan ook gedaan. Nelson redeneerde als volgt: zodra een stekelbaars doorkruipt, vindt er niet nogmaals doorkruipen plaats. Met andere woorden: op de een of andere wijze blokkeert de

[p. 74]

uitvoering van de handeling gedurende enige tijd het nogmaals optreden van die handeling. Denk hierbij maar aan zoiets als bijvoorbeeld het legen van de urineblaas. Wie naar de wc is geweest kan niet meteen nogmaals urineren. Je kunt ook aan een soort vulling denken: wie zijn maag heeft gevuld kan niet meteen nogmaals een hele maaltijd tot zich nemen. Maar bij eten is het effect minder duidelijk omdat je vaak nog wel in staat bent een klein hapje te nemen na een overvloedige maaltijd. Hoe het ook zij, door doorkruipen verandert er iets in de stekelbaars waardoor nogmaals doorkruipen meteen daarna wordt voorkomen. Of er nu iets geleegd wordt tijdens doorkruipen of dat er iets gevuld wordt, weten we voorlopig nog niet, maar we weten wel dat er zoiets gebeurt en in dergelijke gevallen spreken we in onze onmacht maar over de verandering van een variabele in het dier. Nelson noemde die variabele T (van het Engelse ‘threshold’, is ‘drempel’. Het doorkruipen zelf legt een drempel voor het optreden van nogmaals doorkruipen). In het hypothetische model van Nelson wordt nu verondersteld dat die variabele T onder invloed van het doorkruipen stijgt.

Het aanbieden van een vrouwtje vergroot de kans op doorkruipen en die aanbieding heeft lange tijd daarna nog steeds effect want de reeks opeenvolgende doorkruipen volgen met steeds grotere intervallen, waarvan de duur na de eerste twee voorspelbaar is, op elkaar. Het is aannemelijk dat de aanbieding van een vrouwtje een zodanige verandering veroorzaakt van de opwindingstoestand van het dier dat daardoor de kans op doorkruipen vergroot wordt. Nelson noemde die opwindingstoestand E, van het Engelse ‘excitation’ = opwinding, en hij veronderstelde dat E stijgt onder invloed van de aanblik van een vrouwtje. Laten we dat alles nu eens uittekenen in een modelletje (zie afb. 45):

Op tijdstip A bieden wij aan een stekelbaars een vrouwtje aan. Onder invloed van de aanblik op het vrouwtje stijgt de E van de stekelbaars tot een niveau dat wij E_vrouwtje kunnen noemen. Als gevolg daarvan vindt doorkruipen plaats en onder invloed van dat doorkruipen stijgt T tot zijn maximum: T_max. Nu veronderstelde Nelson vervolgens dat de T-factor daarna gaat dalen en dat ook de E-factor, omdat het vrouwtje weg is, daarna gaat dalen. De T-factor daalt echter sneller dan de E-factor en als gevolg daarvan snijden T en E (zie het figuurtje) elkaar op tijdstip B. Op dat moment vindt weer opnieuw doorkruipen plaats en stijgt T weer tot T_max. E blijft dalen en T daalt weer sneller zodat op

[p. 75]

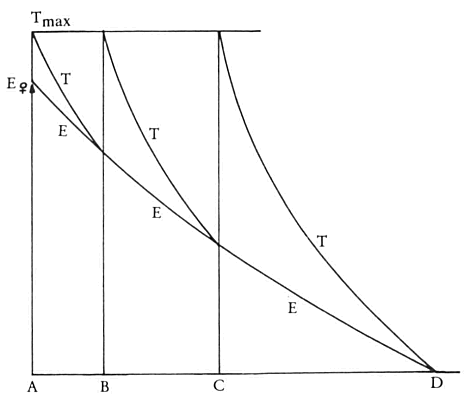
Afb. 45. Model van Nelson

tijdstip C de beide factoren T en E elkaar opnieuw snijden. Weer doorkruipen, weer een stijging van T tot T_max en weer een daling van T totdat T en E elkaar snijden op tijdstip D. In het getekende model is nu duidelijk dat AB:BC = BC:CD ofwel dat CD = BC²:AB

Aangezien we, op grond vooral van het feit dat natuurlijke processen bijna altijd een exponentieel verloop hebben, veronderstellen dat zowel T als E exponentieel zullen dalen, kunnen we nu ook begrijpen waarom een dier dat heel lang geen vrouwtje heeft gezien zo regelmatig doorkruipt. Zijn E is gedaald tot een laag niveau en verandert niet meer. Met andere woorden (kijk ook naar afb. 46): elk interval tussen twee doorkruipen is nu even lang. Meen nu overigens niet dat je het ritme begrijpt; je hebt op deze manier alleen maar een hypothetisch model gemaakt dat ‘past’ op de waargenomen werkelijkheid. Van begrijpen zou pas sprake zijn als je precies zou weten wat T en E nu eigenlijk zijn.

Aan de hand van dit model kun je op zuiver theoretische gronden de volgende voorspelling doen: als ik een vrouwtje aanbied in een glazen buis en dat vrouwtje niet dadelijk na doorkruipen weghaal, maar blijvend aan het mannetje laat

[p. 76]

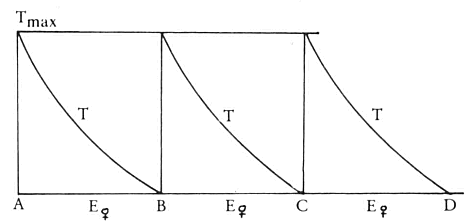
Afb. 46. Doorkruipritme als vrouwtje voortdurend aanwezig is

zien, moet zijn opwindingstoestand (= E) steeds op hetzelfde hoge niveau van E_vrouwtje blijven. Dat houdt in dat volgens het model het mannetje nu heel regelmatig met korte tussenpozen moet gaan doorkruipen.

Toen ik op 1 februari 1966 begon met mijn onderzoek over het gedrag van de driedoornstekelbaars als onderdeel van de voor het doctoraal examen te verrichten arbeid, kreeg ik van Sevenster de opdracht: bekijk of de stekelbaars bij permanente aanbieding van een vrouwtje met regelmatige, korte tussenpozen doorkruipt. Al na een paar dagen kon ik zeggen: dit is bij de dieren die ik tot nu toe heb geobserveerd inderdaad het geval. Als het vrouwtje goed blijft baltsen en het mannetje niet agressief wordt, zal een mannelijke stekelbaars met regelmatige tussenpozen gaan doorkruipen. Om een paar voorbeelden te geven: stekelbaars 12b kroop na aanbieding van een vrouwtje onmiddellijk door; na 15½ minuut ging hij er opnieuw doorheen, na 16½ minuut weer en na 17 minuten weer. Stekelbaars 7B kroop door na aanbieding van een vrouwtje, deed het opnieuw na 25 minuten, nogmaals na 25½ minuut en weer een keer na 27 minuten. De op grond van het Nelson-model voorspelde regelmaat is inderdaad aanwezig (ik heb ze inmiddels bij tientallen dieren steeds weer vastgesteld) maar haast altijd is elk volgend interval ietsje langer dan het vorige, zoals ook uit de twee voorbeelden blijkt. Waarschijnlijk komt dat omdat een mannetje dat permanent een vrouwtje te zien krijgt, gaandeweg agressiever wordt en we weten van agressie dat ze een remmende werking uitoefent op het doorkruipgedrag. Van belang is ook dat het vrouwtje goed blijft baltsen; als zij instort, wordt de man agressief en is het gedaan met het doorkruipritme. Gelukkig zijn er zo nu en

[p. 77]

Afb. 47. Model van een vrouwtje

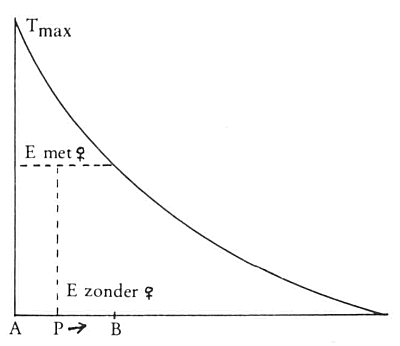
Afb. 48. De kans op een doorkruip

dan mannetjes die op een model van een vrouwtje reageren (zie afb. 47): dit zilveren peertje kun je dan bevestigen aan een motortje (balts-motor in de wandeling) dat het peertje op en neer beweegt in het water. Met zo'n baltsend peertje krijg je, bij die stekelbaarzen die er gevoelig voor zijn, akelig precies gelijke doorkruipintervallen.

De kans op doorkruipen

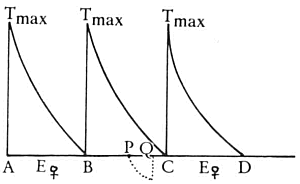
In termen van het model van Nelson valt nu ook te begrijpen waarom het aanbieden van een rijp vrouwtje soms wel, soms geen doorkruipen tot gevolg heeft. Zie maar naar afb. 48. Op tijdstip A heeft een doorkruip plaatsgevonden waarbij geen vrouwtje aanwezig was. De T-factor is gestegen en daalt nu weer, de E-factor is laag. Nu laten we op tijdstip P een vrouwtje zien aan het mannetje, de E-factor stijgt tot het niveau van E_vrouwtje en kan daarbij, afhankelijk van hoever T al gezakt is, T wel of niet snijden. Wordt T

[p. 78]

gesneden dan zal doorkruipen volgen; wordt T niet gesneden dan zal geen doorkruipen volgen. We kunnen zelfs precies zeggen vanaf welk tijdstip het aanbieden van een vrouwtje succes zal hebben. Als A een doorkruip met vrouwtje was geweest en het vrouwtje zou permanent aanwezig zijn dan zou op tijdstip B (de stippellijn geeft de E_vrouwtje aan en die E snijdt de T op tijdstip B) de volgende doorkruip plaatsvinden. Voorbij B is de T-factor nu altijd lager dan E_vrouwtje ofwel voorbij B heeft aanbieding van een vrouwtje altijd doorkruipen tot gevolg. De periode waarin aanbieden van een vrouwtje geen succes heeft, dat wil zeggen, geen doorkruip tot gevolg heeft is exact gelijk aan het doorkruipinterval bij een permanente aanbieding van een vrouwtje.

Dit model geeft je de mogelijkheid na te denken in abstracte termen over het gedrag zonder dat je woorden als agressie, seksualiteit en dergelijke nodig hebt. Bovendien kun je aan de hand van het model voorspellingen doen en experimenten bedenken die je vervolgens kunt uitvoeren om de waarde van je model te toetsen.

Het gedrag tussen twee doorkruipen in

Het model levert bovendien ook de mogelijkheid het gedrag tussen twee doorkruipen in te beschrijven met behulp van die twee factoren T en E. In het model wordt verondersteld dat T en E beide dalen, de een na doorkruipen, de ander na een kortstondige aanbieding van een vrouwtje. T daalt echter sneller dan E. Vlak na doorkruipen zijn T en E maximaal verschillend van elkaar - op dat moment vindt ook het meeste vacuüm-zigzaggen plaats. Het ligt zodoende voor de hand het zigzaggen te beschrijven als de som van E en T. Of in formule ZZ= E+T. Daar E langzamer daalt dan T wordt die som van E plus T voortdurend kleiner, juist zoals in werkelijkheid het vacuüm-zigzaggen voortdurend minder wordt naarmate het doorkruipen langer geleden is. Het waaieren daarentegen komt steeds vaker voor en de waaiervlagen duren steeds langer naarmate de volgende doorkruip nadert. Zodoende ligt het voor de hand het waaieren te omschrijven als het verschil van E en T of in formule Wa= E-T. Nu weet je weliswaar niet wat E en T zijn, laat staan dat je zou weten welk getal je voor E en T zou moeten invullen in die formule, maar je kunt wel uit de je ter beschikking staande waarnemingen van zigzaggen en waai-

[p. 79]

Afb. 49. Alternatief model

eren in de doorkruipintervallen allerlei berekeningen uitvoeren om iets te weten te komen over de factoren E en T. Dit facet van het onderzoek, dat precieze waarnemingen en zorgvuldig rekenwerk met behulp van een computer vereist, staat echter nog in de kinderschoenen, maar wij hopen het binnen niet al te lange tijd toch te gaan uitvoeren.

Een model met twee variabelen?

Is het wel zo nodig om met twee factoren de ritmiek van het doorkruipen in modelvorm te beschrijven? Ligt het niet voor de hand aan te nemen dat slechts één factor die doorkruipritmiek regelt en wel een heel voor de hand liggende: de vullingstoestand van de spermablaas. Zodra die blaas vol is, moet de stekelbaars door het nest heen, een soort van zelfbevrediging. Als die blaas in gelijkmatig tempo gevuld wordt, ligt het voor de hand dat er sprake zal zijn van een precieze ritmiek. Bij het eerder genoemde mannetje dat om de zestig minuten doorkroop zou de blaas dan in precies zestig minuten gevuld worden. En als de aanmaak van sperma nu eens sneller gaat onder de invloed van de aanblik van een vrouwtje verklaart dat meteen waarom de stekelbaars, als er een vrouwtje bij is, vaker doorkruipt. We kunnen ook hier een model van tekenen, nu met slechts één variabele (zie afb. 49).

Welk experiment moeten we nu doen om te onderzoeken of dit model met één dan wel dat andere met twee variabelen de voorkeur verdient? Het volgende: we plaatsen in het aquarium van de stekelbaars een kuitrijp vrouwtje in een glazen buis, we nemen de balts en de doorkruip waar en wachten tot de volgende doorkruip. Na die volgende doorkruip halen we nu enige tijd het vrouwtje weg en plaatsen

[p. 80]

Afb. 50. Model van Nelson

haar weer terug lang voordat we de volgende doorkruip verwachten. Daarna wachten we op de derde doorkruip. Met behulp van het model met twee variabelen kunnen we nu, zie afb. 50, de volgende voorspelling doen over het tijdstip waarop die derde doorkruip zal volgen. Als wij op tijdstip P in het tweede interval het vrouwtje weghalen zal dadelijk de zogenaamde E-factor gaan dalen. Plaatsen wij nu op tijdstip Q het vrouwtje terug in het aquarium dan zal E weer onmiddellijk stijgen tot het normale niveau en dientengevolge zal op tijdstip C doorkruipen plaatsvinden. Het lijkt dan net alsof er in het tweede interval niets gebeurd is want AB = BC als dit model gelijk heeft.

Nu het andere model. Op tijdstip A dus doorkruipen en daarna toename van die ene variabele, misschien de vullingstoestand van de spermablaas, misschien iets heel anders. In het tweede interval halen wij op tijdstip P de vrouw weg. Daar zij nu weg is zal de variabele opeens minder snel gaan stijgen (zie afb. 49). Plaatsen wij op tijdstip Q de vrouw weer terug dan zal de variabele weer op de snellere wijze stijgen onder invloed van de aanwezigheid van het vrouwtje. Daar er gedurende enige tijd sprake is geweest van tragere stijging, heeft dat tot gevolg dat BC langer van duur moet zijn dan AB.

Nu het experiment zelf. De resultaten daarvan waren zonneklaar. BC is altijd gelijk aan AB ofwel het model met slechts één variabele is niet bruikbaar om de doorkruipritmiek te beschrijven.

Om uit te sluiten dat het effect van het weghalen van het vrouwtje in de periode PQ te gering is om een meetbaar verschil in lengte tussen BC en AB te veroorzaken hebben wij in de periode PQ bij een aantal experimenten niet alleen het vrouwtje weggehaald, maar ook het mannetje zelf weggevangen uit zijn eigen aquarium en hebben wij bij weer andere experimenten het mannetje laten vechten tegen een

[p. 81]

ander mannetje. Je kunt de periode PQ bovendien bijna zo lang maken als het interval BC. Volgens het model met de twee variabelen moet dan toch op tijdstip C doorkruipen plaatsvinden, volgens het model met één variabele wordt BC langer naarmate PQ langer is. In werkelijkheid vind je bij geen van al deze experimenten ooit een verlenging van BC; het tweede dk-interval is altijd gelijk aan het eerste wat je ook uitspookt in dat tweede interval. Het enige wat belangrijk is, is dat op de tijdstippen B en C een vrouwtje aanwezig is.

Uit het model volgt nog iets heel anders. Als T en E elkaar snijden, zal doorkruipen plaatsvinden. Als het 's nachts donker is doet de stekelbaars niets, ligt slechts stil op zijn nest. Maar T daalt gewoon verder en heeft E allang gesneden voordat 's morgens het licht aangaat. Dat houdt in dat je moet verwachten dat alle stekelbaarzen 's morgens vroeg dadelijk na het aangaan van het licht zullen doorkruipen. Waarnemingen in de vroege morgen hebben ons geleerd dat stekelbaarzen inderdaad binnen een kwartier na het aangaan van het licht doorkruipen.

Toch is het nog best denkbaar dat of de E-factor of de T-factor iets te maken heeft met de vullingstoestand van de spermablaas. Als echter tijdens doorkruipen sperma wordt afgescheiden moet die sperma na een doorkruip in het nest aanwezig zijn. Om te onderzoeken of dat het geval is hebben wij een pipetkorf ontwikkeld. Dat is een pipet aan het uiteinde waarvan een korfje bevestigd is. Direct na doorkruipen hielden wij dat korfje bij het nest en voordat we het bij het nest hielden vulden we het eerst met afgestreken eieren. (Vrouwtjes kunnen soms zo rijp zijn dat een lichte druk van een vinger tegen haar buik voldoende is om het afleggen van de eieren te bewerkstelligen, zulke eieren kun je dan voor experimenten gebruiken.) Door de pipet heen zogen we water op uit het nest dat eerst het korfje met de afgestreken eieren passeerde. Als er sperma in dat opgezogen nestwater zit, moet tenminste een deel van de eieren in het korfje bevrucht zijn. In werkelijkheid bleek dat ten hoogste 3 of 4 eieren van zo'n afgestreken legsel van 100-200 eieren bevrucht waren. Misschien wordt er wel wat sperma afgescheiden, maar veel kan het niet zijn want als wij direct na een bevruchting het korfje met eieren bij het nest houden en gaan zuigen, blijken alle eieren in de korf bevrucht te zijn.

Maar het vreemdste resultaat van al onze experimenten heb ik tot nu toe nog niet vermeld. Je kunt een stekelbaars

[p. 82]

tegelijkertijd een aantal nesten laten bouwen met behulp van een draaitafel. Dat is een apparaat dat wij in een aquarium kunnen plaatsen met drie gescheiden compartimenten waarvan er steeds één voorgedraaid is. In elk compartiment bevindt zich zand; buiten de draaitafel is geen zand aanwezig, slechts een glazen of een plastic bodem. De stekelbaars zal nu op het zand bouwen. Tijdens de bouw kun je regelmatig een ander compartiment voordraaien en daarmee dwing je hem twee nesten te vervaardigen. Als hij de nesten klaar heeft, bied je een kuitrijp wijfje in een glazen buis aan. Het mannetje zal doorkruipen, zoal niet meteen dan toch na enige tijd. We wachten nu op de tweede doorkruip. Nadat de tweede doorkruip heeft plaatsgevonden draaien we een ander nest voor en bieden een kuitrijp wijfje aan, ditmaal echter los in het aquarium. We laten nu de balts en al wat daarbij hoort, tot en met de bevruchting toe, geschieden en als die bevruchting heeft plaatsgehad, halen we het vrouwtje weg en draaien we het oude nest weer voor. De derde doorkruip zal plaatsvinden op het gewone, te voorspellen (of vaak iets eerder dan verwachte!) tijdstip alsof er in die tussentijd niets is gebeurd. Dit is wel een heel vreemd resultaat. Het bewijst dat de vullingstoestand van de spermablaas geen invloed kan hebben op het doorkruipritme want ook als we tussen twee doorkruipen in een bevruchting laten plaatsvinden (en daarbij wordt de spermablaas geheel geledigd) blijft de ritmiek gewoon gehandhaafd mits we de eieren meteen na de bevruchting weghalen. Het bewijst ook dat bevruchting en doorkruipen weinig met elkaar te maken hebben, een resultaat dat niet zo verrassend is want doorkruipen en bevruchting zijn heel verschillende gedragshandelingen. Bij een doorkruip gaat een stekelbaars langzaam door het nest heen (gemiddelde duur ongeveer 15 sec); bij een bevruchting schiet de stekelbaars door het nest heen (gemiddelde duur ongeveer 3 sec).