Geschiedenis van de wetenschappen in België. 1815-2000

[p. 71]

4 De wiskunde
Jean Mawhin

▪ De variatierekening

Aan de Université libre de Bruxelles lagen de ideeën en het enthousiasme van Théophile De Donder aan de basis van een bloeiende wiskundige traditie. Dankzij zijn leerling Théophile Lepage (1901-1991) kreeg de externe differentiaalrekening, een van de nuttigste hulpmiddelen die tijdens de 20ste eeuw in de wiskunde werden geïntroduceerd, en waarvan De Donder een pionier was, nieuwe toepassingen in de oplossing van een klassiek probleem - de partiële differentiaalvergelijking van Monge-Ampère - en in de synthese van de methoden van Théophile De Donder, Hermann Weyl (1885-1955) en Constantin Carathéodory (1873-1950) in de variatierekening van meervoudige integralen. Door het gebruik van differentiaalvormen worden in deze vraagstukken lange, saaie berekeningen vermeden. De resultaten van Lepage kregen een plaats in de referentiewerken. Zijn methoden inspireren nog steeds de hedendaagse wiskundigen: Boener en Sniatycki spraken van de congruentie van Lepage; onlangs introduceerde Demeter Krupka, naast de euleriaanse vormen die overeenkomen met Eulers klassieke vergelijkingen van de variatierekening, de zgn. lepagiaanse vormen of equivalenten van Lepage in de variatievraagstukken over fiberruimten. Aan Lepage danken we ook interessante resultaten in verband met lineaire voorstellingen van de symplectische groep, en in het bijzonder de ontbinding van Lepage van een buitenste macht van het product van een even aantal kopieën van het complex vlak. Lepage was gedurende 43 jaar lid van de Académie royale de Belgique. Aan de Université libre de Bruxelles onderwees hij differentiaal- en integraalrekening van 1931 tot 1956, en hogere analyse van 1956 tot 1971.

Paul P. Gillis (^o1912), een leerling van Lepage, nam de cursus differentiaal- en integraalrekenen over van 1956 tot 1982. Gillis' onderzoekingen waren

Théophile Lepage. 1939 Brussel. Archives de l'Université libre de Bruxelles ▪

[p. 72]

vooral gericht op de theorie van de differentiaalvormen, de variatierekening en partiële differentiaalvergelijkingen. In 1943 loste Gillis een vraagstuk op dat Elie Cartan had geformuleerd in Leçons sur les invariants intégraux. Het was de bedoeling betekenis te geven aan het belangrijke begrip externe differentiaal van een continue (en niet noodzakelijk afleidbare) vorm vanuit de beroemde formule van Stokes-Cartan die op klassieke wijze de integraal van een differentieerbare vorm op de rand van een variëteit verbindt met de integraal van zijn externe differentiaal op de variëteit. De oplossing van Gillis, vanaf 1945 door Elie Cartan opgenomen in zijn boek Les systèmes extérieurs et leurs applications géométriques, is momenteel geïntegreerd in de theorie van de stromen. Referentiewerken zoals Théorie des distributions van Laurent Schwartz (^o1915) en Variétés différentiables van Georges de Rham (1903-1990) citeren veelvuldig uit de verhandeling van de Brusselse wiskundige. Gillis' resultaten over differentiaalvormen en gewone differentiaalvergelijkingen worden besproken in een van de beroemdste werken over differentiaalvergelijkingen, Ordinary Differential Equations van Philip Hartman (^o1915). Paul Gillis toonde ook belangstelling voor de oplosbaarheid van de Dirichletproblemen voor elliptische, niet-lineaire vergelijkingen met behulp van topologische of variatiemethoden, en schonk aandacht aan vraagstukken over optimale controle en statistiek. Gillis is sinds 1976 lid van de Académie royale de Belgique.

Een andere leerling van Lepage, Robert Debever (1915-1998), hoogleraar aan de Université libre de Bruxelles en lid van de Académie royale de Belgique sinds 1967, wijdde zich aan variatierekening, differentiaalmeetkunde en algemene relativiteit. Belangrijk zijn de opmerkelijke resultaten over elektromagnetische ruimten, behaald in samenwerking met Jules Géhéniau en Paul Libois. Deze wiskundige met een passie voor Belgische literatuur en geschiedenis zorgde tevens voor de publicatie van de interessante briefwisseling tussen Albert Einstein en Elie Cartan.

Léon Van Hove (1924-1990) maakte vooral naam als theoretisch fysicus. Voor hij in Utrecht theoretische fysica ging doceren, behaalde hij evenwel de

Léon Van Hove. Genéve. CERN ▪

titel van doctor in de wiskundige wetenschappen aan de ULB onder leiding van De Donder en Lepage. In 1958 ontving hij de Francqui Prijs; twee jaar later trad hij toe tot de Conseil européen de la Recherche nucléaire (CERN) te Genève, waarvan hij in 1975 algemeen co-directeur werd. Zijn wiskundig werk betreft de variatierekening, de functionele analyse en de mathematische grondslagen van de kwantumtheorie. Erg bekend is zijn antwoord op een vraagstuk van Jacques Hadamard (1865-1963), het klassiek geworden bewijs van een generalisering van de voldoende voorwaarde van Legendre voor het bestaan van een minimum in de variatierekening. Daarnaast kennen we het theorema van Groenwald-Van Hove, wat slaat op de onmogelijkheid de representatie van de metaplectische groep (dubbele bedekking van de symplectische groep) uit te breiden zodat er om het even welke niet-kwadratische polynoom in wordt opgenomen. Vermeldenswaard is ook dat Van Hove belast werd met de redactie van een artikel over de bijdragen van John von Neumann (1903-1957) tot de kwantumtheorie in het kader van een herdenking georganiseerd door de American Mathematical Society. In de mathematische fysica was Van Hove actief op het vlak van de klassieke en kwantum statistische mechanica. Zijn

[p. 73]

artikel over de configuratie-integraal voor de ééndimensionale deeltjessystemen werd opgenomen in een bundel over de ééndimensionale mathematische fysica, uitgegeven door Elliot H. Lieb en Daniel C. Mattis. Van Hove zorgde tevens voor de eerste bevredigende afleiding van de transportvergelijking vanuit de kwantumvergelijking van Liouville.

▪ De wiskundige analyse

Charles-Jean de La Vallée Poussin (1866-1962) verrijkte in de eerste helft van de 20ste eeuw op een briljante manier de theorie van de reële functies. In het begin van de jaren '30 ging de aandacht echter niet alleen naar het werk van de La Vallée Poussin en De Donder, maar ook naar de bijdragen van Florent J. Bureau (1906-1999) over de theorie van functies van complexe veranderlijken. Hij studeerde ingenieurswetenschappen en wiskunde aan de universiteit van Luik en verdiepte zijn kennis en ideeën tijdens stages in Parijs en Berlijn. Een polynoom p(z) = a₀ + a₁z + ... + a_nzⁿ van de graad n in de complexe veranderlijke z vormt het eenvoudigste voorbeeld van een functie van een complexe veranderlijke, en het fundamentele theorema van de algebra verzekert dat voor elk bepaald complex getal c de vergelijking p(z) = c minstens n al dan niet verschillende oplossingen heeft. De natuurlijke veralgemening van een polynoom leidt tot de gehele functies, die kunnen worden geschreven onder de vorm van een oneindige reeks

f(z) = a₀ + a₁z + ... + a^kz^k+...,

convergent voor iedere waarde van z. Het bijzonder geval van de exponentiële functie



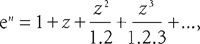
die nooit gelijk wordt aan nul, bewijst dat de vergelijking f(z) = c, met f geheel en niet polynoom, geen enkele oplossing kan hebben voor bepaalde, zgn. uitzonderlijke waarden van c. In 1879 had Emile Picard (1856-1941) aangetoond dat er hooguit één uitzonderlijke waarde bestond (anders gezegd dat een gehele functie die nooit twee verschillende gegeven waarden aanneemt noodzakelijkerwijs constant is), wat - in de woorden van Paul Painlevé (1863-1933) - het pad effent naar ‘een mysterieuze wereld, zo uitgestrekt en rijk dat na vijftig jaren exploreren nog steeds niet alle geheimen zijn ontrafeld’. Op deze mysterieuze wereld wierp Bureau een nieuw licht door onder meer te bewijzen dat een gehele functie die een uitzonderlijke waarde heeft, en waarvan de afgeleide een uitzonderlijke waarde heeft niet gelijk aan nul, noodzakelijkerwijs een constante is. Daarvoor ontwikkelde Bureau efficiënte technieken (waarvan één resultaat in het recente werk Introduction to Classical Complex Analysis van Robert B. Burckel werd omschreven als een ‘amazing lemma’), die een inspiratiebron waren voor buitenlandse wiskundigen zoals Carlo Miranda, Georges Valiron, Henri Milloux en Chi Tai Chuang. In 1935 publiceerde Bureau zijn eerste werken over de hyperbolische differentiaalvergelijkingen. Ze veralgemenen de beroemde vergelijking van de voortplanting van akoestische of elektromagnetische golven. Bureaus onderzoek bouwde voort op een methode die in het begin van de eeuw werd geïntroduceerd door Jacques Hadamard. Deze laatste wees meermaals op het belang van de resultaten van onze landgenoot in de Comptes-Rendus de l'Académie des Sciences. Ook na de Tweede Wereldoorlog genoot het werk van Bureau opnieuw een wereldwijde erkenning en werd het veelvuldig gebruikt en geciteerd in referentiewerken over

Florent J. Bureau (midden), in het gezelschap van Koning Boudewijn (rechts) en Paul Michot (links). Brussel, Académie royale de Belgique ▪

[p. 74]

partiële differentiaalvergelijkingen. Het constructieve aspect van de methode van de singulariteiten om oplossingen te vinden voor partiële differentiaalvergelijkingen vanuit de elementaire oplossing is niet verdrongen door het gebruik van meer abstracte methoden. Bureau heeft zijn technieken toegepast op talloze problemen uit de fysica, zoals de voortplanting van lichtgolven in kristallijne milieus, de golfmechanica van het elektron en de lineaire theorie van de viskeuze, licht samendrukbare vloeistoffen.

Een ander onderzoeksdomein waarin Bureau origineel werk heeft verricht, is de studie van de nietlineaire differentiaalvergelijkingen in het complex veld. Zijn eerste onderzoek op dit domein, over de vergelijkingen van de eerste orde, was zijn aggregatieproefschrift aan de universiteit van Luik (1933). In tegenstelling tot de oplossingen van lineaire vergelijkingen, waarvan de singulariteiten te vinden zijn tussen de singulariteiten van de coëfficiënten van de vergelijking, en dus een vaste waarde hebben, kunnen de oplossingen van niet-lineaire differentiaalvergelijkingen mobiele singulariteiten ontwikkelen, d.w.z. afhankelijk van de initiële voorwaarden. Het past dus eerst de differentiaalvergelijkingen te beschouwen waarvan de oplossingen slechts polen hebben als mobiele singulariteiten (stabiele vergelijkingen of met vaste kritieke punten). Paul Painlevé had rond de eeuwwisseling op magistrale wijze reeds het geval bestudeerd van de vergelijkingen van de tweede orde. De latere Franse staatsman had de vergelijkingen die niet geïntegreerd worden in termen van klassieke transcendente functies teruggebracht tot zes canonieke vormen, vandaag bekend onder de naam vergelijkingen van Painlevé. In 1939 benaderde Bureau dit probleem met een nieuwe methode die de delicate procédés van Painlevé substantieel vereenvoudigde. Hij gebruikte en ontwikkelde deze benadering vanaf de jaren '60 en verkreeg belangrijke resultaten voor de derde-orde differentiaalvergelijkingen en voor stelsels van vergelijkingen. De studie van de stabiele differentiaalvergelijkingen, lange tijd beschouwd als een vraagstuk uit de zuivere analyse, speelt momenteel een belangrijke rol in de analyse van fundamentele niet-lineaire evolutievergelijkingen in de theoretische fysica (vergelijking van Kortweg-de Vries, niet-lineaire vergelijking van Schrödinger en vergelijking van Sine-Gordon).

Bureau werd in verschillende landen uitgenodigd om zijn werk te komen toelichten. De Académie royale de Belgique vierde in 1989 zijn vijftigjarig lidmaatschap, een voorrecht dat hij met slechts drie wiskundigen deelde: Adolphe Quetelet (1796-1874), Jacques Deruyts (1862-1945) en Charles-Jean de La Vallée Poussin. Bureau ontving in 1952 als eerste wiskundige de Francqui Prijs; hij bleef de enige tot in 1988. Op het internationaal congres voor wiskunde te Amsterdam in 1954 zat hij in de jury van de Fields Medaille, de ‘Nobelprijs voor wiskunde’. Hij gaf meer dan veertig jaar les aan de universiteit van Luik, waar hij met zijn sterke persoonlijkheid generaties wiskundigen, fysici en ingenieurs beïnvloedde. Tussen 1932 en 1975 onderwees hij aanvullingen van wiskunde aan natuurkundigen, algebra en theorie van de determinanten, analytische mechanica, mathematische fysica en hogere analyse. Dit resulteerde in de publicatie van een Cinématique en een Calcul vectoriel et tensoriel, uitgegeven bij Sciences et Lettres te Luik, die volgens André Delachet ‘de verdienste heeft in enkele pagina's het essentiële van de theorie te resumeren’, en van een imposante reeks gestencilde notities over de meest verscheiden aspecten van de wiskundige analyse.

Henri-Georges Garnir (1921-1985), een leerling van Bureau, studeerde zowel fysica als wiskunde. Hij begon zijn wetenschappelijke loopbaan aan de universiteit van Luik met onderzoek in de algebra dat was gemotiveerd door vraagstukken uit de theoretische fysica. Zijn bijdrage tot de representatie van symmetrische groepen wordt uitdrukkelijk vermeld in een recent werk van Gordon James en Adalbert Kerber, The representation theory of symmetric group. Vervolgens richtte hij zich op het gebruik van Hilbert-methoden in de studie van problemen op de grens van de mathematische fysica. Hij vatte ze samen in een monografie. Garnir schonk ook aandacht aan de functionaalanalyse, en vooral aan de constructieve studie, door middel van half-normen, van lokaal convexe topologische vectorruimten die de genormeerde vectorruimten

[p. 75]

Henri-Joseph Garnir. Brussel, Académie royale de Belgique ▪

veralgemenen. Dit resulteerde in een driedelig boek, geschreven in samenwerking met twee leerlingen: Analyse fonctionelle. Théorie constructive des espaces linéaires. De publicatie werd gespreid over vijf jaar. Het werk valt op door het feit dat het alleen maar van het aftelbare keuze-axioma gebruik maakt. Garnir keerde daarna terug naar de theorie van de partiële differentiaalvergelijkingen. Hij bestudeerde meer in het bijzonder de voortplanting van de singulariteiten in vraagstukken met limieten voor evolutievergelijkingen. Hij organiseerde drie conferenties om deze vraagstukken te inventariseren en publiceerde er de verslagen van. Garnir animeerde een belangrijke groep onderzoekers (Centre d'analyse fonctionnelle de Liège) en werd zowel in België als in het buitenland bekend als een buitengewoon pedagoog en een ongeëvenaard spreker met een groot gevoel voor humor en duidelijkheid. Zijn pedagogische kwaliteiten kan men beoordelen in de didactische werken, waaronder zijn cursus differentiaal- en integraalrekenen (1958-1976), verrijkt met een uitzonderlijke verzameling oefeningen die de auteur in de loop van zijn onderzoek had verzameld. Garnir onderwees eveneens de cursussen analytische mechanica, hogere algebra en functionaalanalyse en hogere analyse. In 1962 was hij voorzitter van het Belgisch Wiskundig Genootschap; in 1976 werd hij verkozen tot corresponderend lid van de Académie royale de Belgique; in 1983 werd hij erelid van het Institut Grand-Ducal de Luxembourg.

▪ De topologie

De algebraïsche topologie, ontstaan op het einde van de 19de eeuw uit het werk van Henri Poincaré (1854-1912), heeft in de loop van de 20ste eeuw een buitengewone bloei beleefd, waarin ook Belgische wiskundigen hun aandeel hadden. De techniek bestaat erin de meetkundige eigenschappen van figuren die invariant zijn voor continue vervormingen (homeomorfismen) te vertalen in eigenschappen van algebraïsche structuren. Nauwkeuriger gezegd: een topologische ruimte is een verzameling voorzien van een structuur die toelaat de omgeving van een punt (bijvoorbeeld een afstand) te definiëren. De algebraïsche topologie associeert aan bepaalde topologische ruimten, reeksen van groepen, modules of vectorruimten (homoloog of cohomoloog) die bepaalde meetkundige eigenschappen van de invariante ruimten vertalen door homeomorfismen (een- of meerdelig zijn, gaten of hengsels hebben,...). Alfred Errera (1886-1960), hoogleraar aan de Université libre de Bruxelles van 1928 tot 1956, wijdde zijn proefschrift en meerdere publicaties aan het beroemde, in de 19de eeuw geformuleerde vierkleurenprobleem. Dat bestond erin te bewijzen dat vier kleuren volstaan om gelijk welke aardrijkskundige kaart in te kleuren zonder dat twee aan elkaar grenzende landen dezelfde kleur krijgen. Er is maar één bewijs bekend. Het dateert uit 1976 en vereist de inzet van computers. Errera hield zich ook bezig met andere vraagstukken uit de algebraïsche topologie, zoals de theorie van de veelvlakken en het theorema van Camille Jordan (1838-1922) over de enkelvoudige krommen. Errera stichtte samen met Théophile Lepage het seminarie voor wiskundige analyse van de ULB, dat een belangrijke rol speelde bij de opbloei van het departement wiskunde van deze universiteit. Vermeldenswaard is nog dat Errera tijdens de Eerste Wereldoorlog een dienst organiseerde die aan de hand van geluid artilleriestukken opspoorde, en van 1921 tot 1938 over deze vraagstukken een cursus gaf aan de Koninklijke Militaire School.

Het was een leerling van Errera, Guy Hirsch (1915-1993), die het onderzoek in de algebraïsche topologie in België op een echt internationaal niveau

[p. 76]

Alfred Errera. 1941, Brussel, Archives de l'Université libre de Bruxxelles ▪

zou brengen. Aan de Université libre de Bruxelles werd hij doctor in de wetenschappen (1937) en geaggregeerde voor het hoger onderwijs (1948). Van 1949 tot 1962 gaf hij les aan de Rijkslandbouwhogeschool te Gent; vanaf 1957 werkte hij aan de Université libre de Bruxelles - Vrije Universiteit Brussel. Zijn eerste werken over algebraïsche topologie handelden over de theorie van de vaste punten van een afbeelding f van een topologische ruimte in zichzelf, d.w.z. van de elementen x waarvoor geldt f(x) = x. Hirsch heeft zich meer in het bijzonder beziggehouden met het geval waar de topologische ruimte invariant is en de afbeelding f equivariant voor een groep van symmetriën inwerkend op X, door resultaten van Borsuk-Alam met betrekking tot het geval van de oneven afbeeldingen te veralgemenen. Hirsch keerde zich dan naar de studie van de algebraïsche topologie van een belangrijke klasse topologische ruimten, de fiberruimten. Een fiberruimte is grosso modo, lokaal, het topologisch product van een topologische ruimte B, de basis, en een ruimte F, de fiber: iedere fiber bezit een omgeving die homeomorf is aan zijn product met een omgeving van het corresponderende punt van de basis. Klassieke voorbeelden zijn de raakfiberruimte aan een bol of meer algemeen aan een oppervlak (de basis is de bol of het oppervlak en de fibers zijn de raakvlakken), de cilinder en de ring van Möbius, respectievelijk verkregen door de kleine zijden van een rechthoekige band aan elkaar te kleven, in het geval van de ring van Möbius door de zijden een halve draai om te slaan (de basis is een cirkel en de loodrechte segmenten zijn de fibers). Het probleem bij fiberruimten is relaties te leggen tussen de homologie of de cohomologie van de ruimte, de basis en de fiber. In 1941 behandelde Hirsch als eerste een bijzonder geval en loste het op. Kort na de oorlog vonden Guy Hirsch en Jean Leray onafhankelijk van elkaar meerdere belangrijke resultaten; één ervan draagt de naam theorema van Leray-Hirsch. Het recente werk van Jean Dieudonné over de geschiedenis van de topologie citeert rijkelijk uit het werk van Hirsch en beklemtoont de betekenis van zijn benadering voor het later onderzoek van René Thom, Jean-Louis Koszul, Jean-Pierre Serre en Armand Borel. Hirsch stelde een formule voor voor de berekening van de homologie van het quotiënt van een compacte connexe Lie-groep door een gesloten connexe deelgroep van dezelfde rang. Jean-Louis Koszul, Jean Leray en Elie Cartan leverden, onder verschillende hypothesen, bewijzen van deze formule van Hirsch. Guy Hirsch gaf ook een interessant voorbeeld van projectief vlak van octaven, een topologische variëteit met dimensie 16 waarvoor de axioma's m.b.t. de invalsrichting van de rechten van een projectief vlak gelden en die later zou worden bestudeerd door Armand Borel.

De belangstelling van Hirsch voor de wiskunde is niet beperkt gebleven tot de algebraïsche topologie. Hij had ook veel interesse voor de grondslagen en de filosofie van de wiskunde (vooral van de waarschijnlijkheidsrekening), en voor de wetenschapsgeschiedenis. Hij redigeerde het hoofdstuk over de algebraïsche topologie in een bekend collectief werk onder leiding van Jean Dieudonné, Abrégé d'histoire des mathématiques, 1700-1900. Ook was Hirsch vanaf 1947 secretaris van het Belgisch Wiskundig Genootschap. Voor het Bulletin ervan maakte hij meerdere lange analyses van boeken. Ze overstegen de eenvoudige kritiek of beschrijving en waren eigenlijk korte monografieën over het thema van het geanalyseerde boek. Het Belgisch Wiskundig Genootschap heeft hem vereerd met een uitgave van een selectie uit zijn werk, wat nog meer

[p. 77]

uitstraling gaf aan zijn bijdrage tot de wiskunde. Hirsch was lid van de Koninklijke Academie van België, het Nationaal Comité voor Wiskunde en het Nationaal Comité voor Logica, Geschiedenis en Filosofie van de Wetenschappen.

▪ De algebra

Gustave Verriest (1880-1951), een leerling van de La Vallée Poussin, was een man met een grote ontwikkeling. In 1925 stichtte hij de Kring der Vlaamse Professoren. Hij was een overtuigd aanhanger van de tweetaligheid aan de Leuvense universiteit en lid van de Koninklijke Academie van België. Hoewel hij geen belangrijk origineel werk heeft nagelaten, introduceerde hij te Leuven de methodes van de moderne algebra die hij in Göttingen had geleerd en schreef hij waardevolle handboeken en algemene werken. Hij was een uitmuntende vulgariserend auteur over wiskunde, die in 1948 voor de Belgische radio een reeks van vier gesprekken over de wiskunde samenstelde.

Robert F. Ballieu (1914-1980) had aan de universiteit van Leuven een zware onderwijstaak te vervullen: algebra en analyse, methodologie van de wiskunde, projectieve meetkunde en waarschijnlijkheidsrekening. Na briljante wiskundestudies te Leuven en een verblijf aan de Ecole normale supérieure te Parijs bestudeerde Ballieu, in navolging van Paul Montel (1875-1975), de begrenzing en de lokalisering van de nulpunten van polynomen van een complexe veranderlijke. Het is een vraagstuk dat teruggaat tot Augustin-Louis Cauchy (1789-1857), die in 1829 bewees dat alle complexe wortels van de vergelijking

a_nzⁿ + a_n-1z^n-1 + ... + a₁z + a₀ = 0

een kleinere modulus hebben dan de positieve wortel van de vergelijking

|a_n|xⁿ - |a_n-1|z^n-1 - ... -|a₁|x + |a₀| = 0

Ballieu heeft in 1936 de optimale grenzen gevonden voor p wortels van bepaalde vergelijkingen, in functie van de p eerste coëfficiënten a₀, a₁,..., a_p-1, van de vergelijking. Zijn resultaat is een uitbreiding van het klassieke theorema van Cauchy en omvat, als bijzondere gevallen, resultaten van Van Vleck en Montel. De bijdragen van Ballieu werden becommentarieerd in het verzameld werk van Montel en worden ook geciteerd in het referentiewerk over de geometrie van de polynomen van Morris Marden (1905-1991).

▪ De toegepaste wiskunde

Georges Lemaître (1894-1966) kennen we vooral als vader van de theorie van het uitdijend heelal en de big bang. Maar ook zijn bijdrage tot de wiskunde, die gaat van de theorie van de elliptische integralen over de numerieke analyse en het elementair rekenen tot de theoretische mechanica, was belangrijk. Lemaîtres doctoraatsverhandeling (het equivalent van de huidige licentie), geredigeerd onder leiding van Charles-Jean de La Vallée Poussin, handelde over de benadering van functies van meerdere veranderlijken door polynomen. De studie van de beweging van drie puntmassa's onderworpen aan de gravitatiewet van Newton (het befaamde ‘drielichamenprobleem’) leidde tot een stelsel differentiaalvergelijkingen waarbij singulariteiten optreden die corresponderen met botsingen tussen de lichamen. De regularisatie van dit probleem bestaat uit de introductie van nieuwe coördinaten die de dubbele schokken doen verdwijnen. Een dergelijk coördinatenstelsel is door Lemaître ingevoerd tussen 1952 en 1954 en draagt zijn naam. We onthouden ook Lemaîtres passie voor rekenmachines. In de jaren '50 introduceerde hij aan de Leuvense universiteit de eerste elektronische rekenmachine. Lemaître had ook veel interesse voor het aanleren van de elementaire rekentechnieken en stelde voor nieuwe cijfers te gebruiken: ‘Zal men zich onnodig blijven vermoeien, anderen een vermoeidheid blijven opleggen die men zou kunnen vermijden door de traditionele routine van zich af te zetten, en een einde te maken aan de Arabische overheersing, door van de drempel van de beschaving het spectrum van Pythagoras te verwijderen? Ik weet hoezeer dit voor sommigen utopisch kan lijken, en toch kan ik niet beletten te denken dat indien deze rekentechnieken en deze nieuwe cijfers werkelijk worden uitgetest, verbeterd en uiteindelijk aanvaard zullen

[p. 78]

worden. Maar zal men het proberen? Chi lo sa?’ We kennen het antwoord: niet de nieuwe cijfers maar de rekenmachines hebben onze rekengewoonten gewijzigd. De bedenker van de oeratoomhypothese werd met eerbewijzen overladen: hij was de eerste laureaat van de Francqui Prijs (1934), lid (1940) en voorzitter (1960) van de Pontificale Academie voor Wetenschappen, lid van verschillende andere buitenlandse academiën en doctor honoris causa van meerdere universiteiten, laureaat van de tienjaarlijkse prijs voor toegepaste wiskundige wetenschappen voor de periode 1933-1942. De Académie royale de Belgique, waarvan Lemaître gedurende meer dan dertig jaar lid was, heeft de honderdste verjaardag van zijn geboorte gevierd met de publicatie van een selectie uit zijn wetenschappelijk oeuvre. De onderwijsmethoden die Lemaître hanteerde (aan de universiteit van Leuven) pasten zeker niet in de fast-food-pedagogie die vandaag door sommigen wordt opgehemeld. Zijn minachting voor administratie was spreekwoordelijk. De moderne opvattingen zouden zeker niet kunnen rekenen op het enthousiasme van deze kleurrijke kanunnik.

Maurice Anthony Biot (1905-1985) studeerde eerst voor ingenieur en werd daarna doctor in de wetenschappen aan de universiteit van Leuven. Hij was onderzoeker bij Caltech en het NFWO. In Harvard begon hij zijn loopbaan als hoogleraar. Hij werkte achtereenvolgens aan de universiteiten van Leuven, Columbia en Brown. Samen met Theodor von Kármán (1881-1963) schreef Biot Mathematical Methods in Engineering, een van de beroemdste werken over toegepaste wiskunde in het Engelse taalgebied. Het werd vertaald in het Frans, het Spaans, het Portugees, het Russisch, het Turks, het Japans, het Pools, het Hongaars en het Italiaans. Biots werken handelen hoofdzakelijk over verschillende aspecten van de mechanica van de continue media en hun toepassingen in de luchtvaart en de mechanica van de poreuze gronden. Om poreuze stoffen te beschrijven voegde Biot twee supplementaire coëfficiënten toe aan de beroemde coëfficiënten van Lamé - vandaag bekend als de coëfficiënten van Biot - en ontwikkelde een theorie over de voortplanting van golven in deze stoffen. Zijn studies van de mechanica van sondes onderworpen aan een initiële druk hebben toepassingen in de

Reclame voor een IBM-rekenmachine. Gent. Archief Universiteit Gent ▪

[p. 79]

Georges Lemaître en de ‘rekenmachines’ van de Leuvense universiteit. Louvain-la-Neuve. Université catholique de Louvain, Archives Lemaître ▪

geologie en de studie van composietmaterialen. Biot ontwierp eveneens een nieuw theoretisch kader voor de thermodynamica. Ook hij heeft veel eerbewijzen ontvangen, zowel in de USA, waar hij lid werd van onder meer de American Academy of Art and Science en de Timoshenko-Medaille en de Théodore von Kármán-Medaille ontving, én in België, waar hij geassocieerd lid van de Académie royale de Belgique, doctor honoris causa van de universiteit van Luik en laureaat van de André Dumont Prijs van de Leuvense ingenieursvereniging werd.

Louis Bouckaert (1909-1988), een leerling van de theoretische fysicus Charles Manneback (1894-1975), studeerde voor ingenieur te Leuven. Hij werd docent in 1937 en gewoon hoogleraar in 1941. Ook na de scheiding van KULeuven en UCL bleef hij professor aan beide instellingen. In de jaren '30 verbleef Bouckaert aan het Institute for Advanced Study in Princeton, waar hij bevriend geraakte met de beroemde Franse wiskundige André Weil (1906-1998). Via niet gesigneerde, aan Bouckaert overgemaakte brieven - die ze ondertekende en naar Frankrijk doorstuurde - kon de wegens de mobilisatie naar Finland gevluchte Weil tijdens de oorlog zonder gevaar communiceren met zijn echtgenote. In 1936 publiceerde Bouckaert samen met Wigner en Schmoluchowski een beroemd werk over de theorie van de zones van Brillouin en de symmetrie van de golffuncties in kristallen. Het wiskundig belang ervan ligt in de constructie van de eerste oneindige representaties van oneindige groepen. Terug in Leuven vatte Bouckaert met de hem eigen bekwaamheid en minzaamheid een zware onderwijsopdracht aan in de wiskunde, de mechanica en de mathematische fysica. Hij was lid van de Koninklijke Academie van België en ondervoorzitter van het Nationaal Comité voor Wiskunde.

▪ De organisatie van het wiskundig onderzoek

Het Nationaal Fonds voor Wetenschappelijk Onderzoek (FNRS-NFWO) werd op 2 juni 1928 opgericht als gevolg van de opmerkelijke redevoering van Koning Albert in 1927. Hoewel de Belgische wiskundigen geen hoge financiële eisen stelden en dus geen groot aandeel hadden in de verdeling van de kredieten en subsidies van deze belangrijke instelling, kregen zij toch voortdurend en onder diverse vormen hulp van dit Fonds: de mandaten van aspirant, onderzoeksstagiair, bevoegdverklaard navorser, onderzoeksdirecteur; de toekenning van onderzoekskredieten (sinds 1946); steun voor de organisatie van wetenschappelijke congressen; contactgroepen. Het wiskundig leven in België werd er ingrijpend door getransformeerd. Hopelijk heeft het Fonds voor Wetenschappelijk Onderzoek, dat momenteel volledig is gefederaliseerd en zoals andere instellingen te kampen heeft met een

[p. 80]

gebrek aan belangstelling voor fundamenteel onderzoek vanuit een bepaalde hoek, zijn mooiste jaren nog niet achter de rug.

Een andere, thans verdwenen instelling (indien niet op papier dan toch de facto) gaf een kwarteeuw lang een impuls aan de Belgische wiskunde waarvan de gevolgen nog steeds voelbaar zijn. Op voorstel van de professoren wiskunde van de universiteiten van Brussel en Luik besloten Minister van Openbaar Onderwijs Camille Huysmans en zijn secretaris-generaal J. Kuypers in 1948 tot de creatie van het Belgisch Centrum voor Wiskundig Onderzoek. Dit centrum werd belast met de organisatie van internationale colloquia over een specifiek probleem, de organisatie van lezingen door wiskundigen op doorreis, de ontwikkeling van wiskundige rekencentra, en het bevorderen van de deelname van jonge Belgische wiskundigen aan conferenties in de Belgische universiteiten. De 25 colloquia die het Centrum tussen 1949 en 1972 organiseerde, waren opmerkelijk door de kwaliteit van de deelnemers en lagen aan de basis van meerdere belangrijke theorieën. Doordat ze alle tendensen in België én de grote hedendaagse stromingen (algebraïsche meetkunde, algebraïsche topologie, differentiaalmeetkunde, functies van meerdere veranderlijken, differentiaalvergelijkingen, mathematische statistiek, getallentheorie, algebra, theorie van de reeksen, relativiteit, numerieke analyse, nietlineaire differentiaalanalyse) bestreken, stelden deze colloquia de Belgische wiskundigen in staat beroemde mathematici te beluisteren en te ontmoeten, vb. Adams, Behnke, Bergmann, Borel, Cartan, Cartier, Conti, Darmois, Eckmann, Ehresmann, Eilenberg, Erdös, Favard, Fenchel, Garnier, Hopf, Kähler, Köthe, Leray, Lichnerowicz, Lions, Mac Lane, Montel, Mordell, Nirenberg, Olech, Orlicz, de Rham, Roth, Schouten, Severi, Serre, Picone, Santalo, Schwartz, Segre, Thom, Van der Waerden, Weil, Whitehead en Yosida. De verslagen van al deze colloquia werden gepubliceerd. Zij vormen één van de parels van de Belgische wiskundige publicaties. Bij de oprichting van het Centrum werd Charles-Jean de La Vallée Poussin tot erevoorzitter verkozen. Een van de eerste taken van het Centrum was de publicatie van het laatste overzichtswerk van de Nestor van de Belgische wiskunde. Lucien Godeaux (1887-1975) was voorzitter van het Centrum van 1948 tot 1966. Hij was er de grote bezieler van tijdens haar meest actieve periode.

Godeaux was, samen met Théophile De Donder en Alfred Errera, medeoprichter van de Wiskundige Kring (1921), die in januari 1922 werd omgedoopt tot Belgisch Wiskundig Genootschap. De Donder werd de eerste voorzitter. Guy Hirsch, het grote werkpaard van het Genootschap na de Tweede Wereldoorlog, was secretaris vanaf 1947 tot aan zijn dood. Het Belgisch Wiskundig Genootschap organiseerde wiskundige bijeenkomsten en publiceerde vanaf 1948 het Bulletin de la Société mathématique de Belgique, tussen 1977 en 1993 aangevuld met de B-reeks Bulletin de la Société mathématique de Belgique - Tijdschrift van het Belgisch Wiskundig Genootschap. Sinds 1994 draagt het tijdschrift als titel Bulletin of the Belgian Mathematical Society - Simon Stevin, aangezien het is samengesmolten met het te Gent uitgegeven tijdschrift Simon Stevin. Het Bulletin heeft steeds synthesewerken en onderzoeksrapporten gepubliceerd. Meerdere jonge Belgische wiskundigen publiceerden er hun eerste onderzoek. Het tijdschrift geeft een vrij precies beeld van het wiskundig onderzoek in België in de tweede helft van de 20ste eeuw. Vrij snel werden er ook uitvoerige besprekingen van werken in opgenomen, de meeste van de hand van Guy Hirsch.

We vermelden tot slot nog het Nationaal Comité voor Wiskunde, een emanatie van de Académie royale de Belgique en de Koninklijke Vlaamse Academie van België. Het heeft tot doel de studie van de verschillende disciplines van de wiskunde in België te bevorderen en te coördineren. Bovendien verzorgt het de relaties met de Internationale Unie voor Wiskunde.

▪ De strijd rond de moderne wiskunde

Het verhaal over de Belgische wiskunde in de tweede helft van de 20ste eeuw zou niet volledig zijn zonder aandacht te besteden aan de twisten en heisa die gepaard gingen met de invoering van de moderne wiskunde in het lager en middelbaar

[p. 81]

onderwijs. Indien een buitenaards wezen de pers van de eerste 150 jaar van de Belgische onafhankelijkheid kon analyseren, dan zou het waarschijnlijk concluderen dat dit de enige belangrijke gebeurtenis in de wiskunde is geweest. Het is immers de enige gebeurtenis die meermaals met sprekende titels de koppen van kranten of tijdschriften heeft gehaald.

De introductie van de taal van de verzamelingenleer en de axiomatische methode hebben geleidelijk het uitzicht van de wiskunde veranderd. Juist voor de Tweede Wereldoorlog besloot een groep Franse wiskundigen onder het pseudoniem Bourbaki de wiskunde in zijn geheel te herschrijven. Ze hielden rekening met de moderne evolutie en gingen van de meest algemene naar de meest bijzondere structuren. Hun ontegensprekelijk wetenschappelijk inzicht ging hand in hand met een zeker intellectueel terrorisme. De groep heeft bijzonder veel invloed uitgeoefend op de naoorlogse ontwikkeling van de wiskunde. In verschillende landen dachten sommigen er ook aan deze revolutie door te voeren in het middelbaar onderwijs.

Deze beweging vond in België een groot voorvechter in de persoon van Georges Papy (^o1920), een leerling van Lepage. Vanaf 1956 was hij professor algebra aan de Université libre de Bruxelles. Omdat hij niet langer in een ivoren toren wilde werken aan de theorie van de gealterneerde vormen begon hij belangstelling te tonen voor experimenten in verband met de vernieuwing van het wiskundeprogramma voor aspirant-kleuterleidsters, van wie werd gezegd dat ze niet veel aanleg hadden voor wiskunde. Op 24 mei 1961 creëerde hij het Centre belge de Pédagogie mathématique (CBPM). Het doel ervan was ‘de studie, de verbetering en de hervorming van het wiskundeonderwijs, en in het bijzonder de promotie, de ontwikkeling en de verspreiding van het onderwijs van de moderne wiskunde’. De uitdrukking moderne wiskunde werd op handige wijze gelanceerd. Iedere opposant werd afgeschreven als een traditionalist of een reactionair. Er was enkel keuze tussen de nieuwe ‘mathématique de Papy’ en de ‘mathématique de papa’! Beroepswiskundigen, ingenieurs en natuurkundigen traden met elkaar in het strijdperk en bestookten elkaar onafgebroken met wetenschappelijke én emotionele argumenten tijdens bewogen bijeenkomsten waar de leraars uit het middelbaar, de ouders van de leerlingen en de stomverbaasde journalisten zich meestal tevreden moesten stellen met het tellen van de punten. Papy had slaafse volgelingen en overtuigde tegenstanders. De reeds behoorlijk uit de hand gelopen twist kreeg nog een politiek tintje toen de aftredende Minister van Openbaar Onderwijs een omzendbrief ondertekende die de invoering regelde van de moderne wiskunde in het begin van het schooljaar 1968.

Ondanks het enthousiasme van de gangmakers, waardoor de interpretatie van de eerste experimenten enigszins werd vertekend, en de omscholing vanuit verschillende instanties, waren de leraars helemaal niet voorbereid. De nieuwe handboeken

Georges Papy tijdens een les moderne wiskunde in een lagere school. Brussel, Persagentschap Belga ▪

[p. 82]

bereikten zelden het niveau van de indrukwekkende verzameling die Papy had gepubliceerd. In 1972 verklaarde Papy zelf aan de pers: ‘De boodschap van de promotors van de hervorming van het wiskundeonderwijs is overal ter wereld zoek geraakt... het schip van de hervorming is gestrand’. Een nieuwe, minder gemediatiseerde hervorming vond plaats in 1978.

Nicolas Rouche (^o1925), hoogleraar aan de Université catholique de Louvain en specialist in de stabiliteit van de differentiaalvergelijkingen, is ook een wiskundepedagoog. In 1982 stelde hij: ‘De bocht van de wiskunde in 1968 is ongetwijfeld nodig geweest. [...] Maar men heeft onnodig een te formele, te symbolische wiskunde ingevoerd. [...] Het fundamentele gebrek dat moest worden overbrugd situeerde zich op het vlak van de intuïtie en op dat van de door de hervorming zwaar gehavende meetkunde’. In 1977 stichtte Rouche, die erg gevoelig is voor de epistemologische en historische aspecten van het wiskundeonderwijs, de Groupe d'Enseignement mathématique. Sinds 1992 is hij de drijvende kracht achter het Centre de Recherche sur l'Enseignement des Mathématiques (CREM), dat gevestigd is te Nijvel. De belangrijkste doelstelling ervan is het onderzoek van het wiskundeonderwijs in Franstalig België, van kind tot volwassene, en de permanente vorming van wiskundeleraren.

Na 1968 wisselden de hervormingen en tegenhervormingen elkaar af. Het debat is nog lang niet gesloten. De talrijke bijeenkomsten en witboeken over het wiskundeonderwijs leveren het bewijs. Na een te lange periode van immobiliteit, gevolgd door een golf van hervormingen, is het voor het onderwijs van de elementaire wiskunde moeilijk om de stijl en de programma's te vinden die het mogelijk maken de 21ste eeuw succesvol en doeltreffend aan te vatten. Maar dat is een probleem dat zeker niet alleen beperkt is tot de wiskunde.

▪ De Belgische wiskundigen in het buitenland

Hoewel we niet genoeg afstand kunnen nemen om een juiste beoordeling te geven van de bijdragen van de talentrijke wiskundigen die momenteel aan onze universiteiten actief zijn, zou het spijtig zijn enkele Belgische wiskundigen onvermeld te laten die buiten de landsgrenzen een onbetwistbare reputatie hebben opgebouwd.

Jacques Tits (^o1930) is momenteel hoogleraar aan het Collège de France. Als wonderkind werd hij in december 1944 de primus van het toelatingsexamen van de ULB. In januari 1945 begon hij op veertienjarige leeftijd aan de eerste kandidatuur wiskunde! Op zijn achttiende was hij licentiaat. Op 19-jarige leeftijd werd hij doctor met een proefschrift, onder leiding van Paul Libois, over de classificatie van exact n-transitieve eindige groepen (dat de resultaten van Zassenhaus bevestigde en uitbreidde), en over de groepen affiniteiten en projectiviteiten. Tits verbleef meerdere jaren aan het Institute for Advanced Study in Princeton en aan het ETH te Zürich. Daar bekwaamde hij zich in de theorie van de Lie-groepen, die een centrale plaats innemen in de huidige wiskunde. Alhoewel reeds benoemd als docent (1957) en hoogleraar (1962) aan de ULB, aanvaardde Tits in 1964 een leerstoel aan de universiteit van Bonn. Hij verbleef er tien jaar, waarna hij het Collège de France vervoegde voor de leerstoel Théorie des Groupes. Tits is doctor honoris causa van meerdere universiteiten (waaronder Gent en de UCL in België), is lid van het Institut de France en van meerdere wetenschappelijke genootschappen (waaronder de Académie royale de Belgique), en heeft talrijke wetenschappelijke onderscheidingen gekregen, zoals de prestigieuze Wolf-Prijs (1993), die hij deelt met Mikhael Gromov (^o1943). Er is waarschijnlijk geen betere beoordeling van zijn bijdrage tot de wiskunde dan degene die bij de toewijzing van deze prijs werd gegeven: ‘Tits heeft verschillende fundamentele bijdragen geleverd tot de theorie van de groepen en hun interactie met de meetkunde. Hij heeft de flattheorie ontwikkeld als centraal principe en als krachtig hulpmiddel voor een verbazend breed spectrum van problemen in de groepentheorie en in de meetkunde. Deze meetkundige benadering in de groepentheorie is toepasbaar op eindige, p-adische en aritmetische groepen, en heeft nuttig werk geleverd in de meeste grote ontwikkelingen van de laatste twintig jaar. Omgekeerd gebruikt zijn

[p. 83]

werk de groepentheorie ook om talrijke diepgaande bijdragen tot de meetkunde mogelijk te maken’. Een ‘flat’ is een simpliciaal complex dat de vereniging is van subcomplexen, die appartementen worden genoemd en aan een aantal voorwaarden voldoen. Deze objecten liggen aan de oorsprong van gewaagde wiskundige speculaties. Tits' methoden zijn van het grootste belang geweest voor een van de spectaculairste verwezenlijkingen van de moderne algebra, nl. de volledige classificatie van de eindige simpele groepen, voltooid in 1981, en in het bijzonder voor de studie van het ‘monster’ van Fischer-Griess, dat meer dan 10⁵⁴ elementen telt.

David Ruelle (^o1935) studeerde aan de Faculté polytechnique van Mons en de ULB, waar hij in 1959 doctor in de wetenschappen werd. Hij was onderzoeksassistent en ‘Privatdozent’ aan het ETH te Zürich en lid van het Institute for Advanced Study in Princeton. Sinds 1964 is hij hoogleraar aan het Institut des Hautes Etudes scientifiques van Bures-sur-Yvette (Frankrijk). Zijn werken handelen over mathematische fysica en de theorie van de dynamische systemen. In de mathematische fysica bedacht hij een asymptotische voorwaarde die de definitie van de S-matrix in de kwantum veldtheorie toelaat alsook een definitie en een studie van de evenwichtstoestanden en toestanden van Gibbs voor oneindige systemen. In de theorie van de dynamische systemen heeft hij samen met de Nederlander Floris Takens aangetoond dat vreemde attractoren een rol spelen in de verklaring van de turbulentie, wat intussen experimenteel bewezen is. Hij is dus een van de ontwerpers van de chaostheorie, één van de nieuwe paradigma's van de hedendaagse wetenschap. Naast gewaardeerde handboeken schreef Ruelle ook een opmerkelijk en boeiend vulgariserend werk, Hasard et chaos. Nooit heeft hij geaarzeld om de betreden paden te verlaten. Ruelle is lid van het Institut de France en doctor honoris causa van meerdere universiteiten (waaronder die van Mons-Hainaut). In 1979 ontving hij in Monaco de Prix Albert I^er.

De loopbaan van Pierre Deligne (^o1944) gelijkt sterk op die van Tits. Hij was pas twintig toen hij in 1966 na twee jaar studie slaagde in het licentieexamen wiskunde aan de ULB. Op aanraden van

Jacques Tits. Brussel, FNRS ▪

Tits liep hij ook stage in Parijs. Hij maakte zijn proefschrift in Parijs, maar verdedigde het te Brussel in 1968. Ondanks zijn benoeming als docent aan de ULB, weerstond Deligne niet aan de lokroep van het Institut des Hautes Etudes scientifiques van Bures-sur-Yvette. Vanaf 1968 was hij er gastprofessor en werkte hij er samen met Alexandre Grothendieck (^o1928). In 1970 werd hij er vast hoogleraar, maar in 1968 verliet Deligne Frankrijk voor een leerstoel aan het Institute for Advanced Study in Princeton. Delignes bijdragen betreffen hoofdzakelijk de algebraïsche meetkunde, d.w.z. de studie van het geheel van de oplossingen van veeltermvergelijkingen (algebraïsche variëteiten), in het bijzonder over eindige lichamen. Zijn gemengde Hodge-theorie heeft meerdere toepassingen in de studie van families van projectieve variëteiten, van differentiaalvergelijkingen op een algebraïsche variëteit, en in de homotopie van de complexe variëteiten. In 1971 bewees Deligne een hypothese die André Weil in 1949 had geformuleerd over de eigenschappen van een zetafunctie (analoog aan die gebruikt door Charles-Jean de La Vallée Poussin en Jacques Hadamard voor het bewijs van het theorema van de priemgetallen), die de aritmetische informatie van de algebraïsche variëteiten encodeert op een eindig lichaam. De oplossing van de hypothese van Weil

[p. 84]

Pierre Deligne. Brussel, FNRS ▪

Jean Bourgain. Privé-collectie ▪

had meerdere gevolgen voor de getallentheorie. Zij bezorgde Deligne in 1975 de vijfjaarlijkse prijs van het FNRS en in 1978 de Fields-Medaille. In 1988 kreeg hij de prestigieuze Crafoord-Prijs, samen met Alexandre Grothendieck (die hem weigerde). Deligne is lid van het Institut de France, de Amerikaanse Academie voor Kunsten en Wetenschappen en de Académie royale de Belgique.

Jean Bourgain (^o1954) studeerde wiskunde aan de Vrije Universiteit Brussel. In 1977 werd hij op drieëntwintigjarige leeftijd doctor in de wetenschappen onder de leiding van F. Delbae. Eerst was hij onderzoeker bij het NFWO en gastprofessor aan de universiteiten van Paris VI, Orsay en Chicago. In 1985 werd Bourgain benoemd tot hoogleraar aan de VUB. Hij werd ook titularis van de Doob-leerstoel aan de University of Illinois te Urbana. In 1985 was hij laureaat van de vijfjaarlijkse prijs van het NFWO. Het jaar daarop volgde hij Deligne op aan het Institut des Hautes Etudes scientifiques te Bures-sur-Yvette. In 1993 vervoegde hij het Institute for Advanced Study in Princeton en in 1994 ontving hij de Fields Medaille. Volgens Luis Caffarelli (^o1948) bestrijkt het oeuvre van Bourgain ‘meerdere centrale domeinen van de wiskundige analyse: de meetkunde van Banachruimten, convexiteit in hogere dimensie, harmonische analyse, de ergodische theorie en de niet-lineaire differentiaalvergelijkingen van de mathematische fysica. In al deze vraagstukken is hij erin geslaagd spectaculaire vooruitgang te boeken op punten waar de progressie al gedurende een hele tijd was gestaakt. Deze vooruitgang werd gerealiseerd door een beroep te doen op meerdere wiskundige domeinen tegelijk: de getallentheorie, de combinatorische analyse, de waarschijnlijkheidsleer.’ De werken van Bourgain, die met succes problemen behandelen waar zijn voorgangers voor terugschrokken, getuigen van een buitengewoon analytisch vermogen, en hebben nog lang niet al hun geheimen prijsgegeven.

Hoewel al deze wiskundigen van Belgische afkomst in het buitenland respect afdwingen, is het bitter om vast te stellen dat het in eigen land onmogelijk is gebleken om een Institut des Hautes Etudes scientifiques of een Institute for Advanced Study op te richten. De Belgische wetenschap wacht dan ook met ongeduld op een nieuwe redevoering van Seraing.