Geschiedenis van de wetenschappen in België van de Oudheid tot 1815

[p. 179]

Patricia Radelet-de Grave
De natuurkunde

▪ Van kosmologie tot praktische problemen: het werk van de natuurkundigen

De ingrijpende verandering teweeggebracht door de hypothese van Copernicus beperkte zich niet uitsluitend tot de visie op het universum of tot de nieuwe plaats van de mens in dit geheel. Zij had ook betrekking op het aardse en vereiste een herziening van de natuurkunde, aangezien de onderzoekers juist daarin bewijzen hoopten te vinden die het heliocentrisme bevestigden of ontkrachtten. Deze beweging was universeel, en de Belgische auteurs waren dan ook geen uitzondering. Velen waren door hun banden met de Kerk verhinderd hun gedachten even duidelijk te formuleren als Galilei in zijn Dialogo. Toch kunnen we vaststellen dat ze zich met dezelfde onderwerpen hebben beziggehouden.

De tegenstanders van het heliocentrisme schermden met de door Aristoteles voorspelde chaos, die zou heersen als de aarde door om het even welke beweging werd aangedreven. Volgens hen zouden de voorwerpen in dat geval onderhevig zijn aan een middelpuntvliedende kracht die ze in de ruimte zou slingeren. Het werk van Galilei, Descartes, Huygens en alle natuurkundigen van toen was er dan ook op gericht de natuurkunde te herschrijven in de context van deze bewegende aarde.

Niet zonder reden verschenen in deze periode de eerste omschrijvingen van het relativiteitsprincipe en werd ook het probleem van de worp belangrijk. Hoewel men zijn bewering in twijfel kan trekken, deelt Libertus Fromundus (1587-1653) ons in een tekst van 1631 mee dat Jean Gallé (1616-1635) waarnemingen verrichtte om de afwijking te ontdekken die werd toegeschreven aan de rotatie van de aarde. Hij deed dit door de val van een blok lood, vanuit de top van een mast van een galei naar beneden geworpen, te observeren. Het probleem van de worp was nog sterk gelieerd met de militaire imperatieven van de artillerie. Laat ons niet vergeten dat dit probleem, ook al vond het een oplossing in de mechanica van Galilei, pas volledig begrepen zou worden toen Isaac Newton (1642-1727) Galilei's aardse en Keplers hemelse bewegingen met elkaar verenigde.

Simon Stevin (1548-1620), een verdediger van Copernicus, trok in 1585 de beweging op gang. De inhoud van zijn werk is sterk getekend door zijn ervaring als ingenieur: krijgsvoering en vestingbouw, eenvoudige toestellen en hijswerktuigen, de toom van paarden. Anderzijds bespreekt hij ook onderwerpen als de statica en de hydrostatica, die eveneens door Galilei zouden worden behandeld. Deze thema's, die men als aards zou kunnen omschrijven, stonden ook bij heel wat Belgische onderzoekers, zoals Gregorius a Sancto Vincentio, Jan-Karel della Faille en Gilles-François de Gottignies, in het middelpunt van de belangstelling. Uit allerlei details zal blijken dat ze de kosmologie steeds in gedachten hielden.

Ook de studie van de slingerbeweging trok hun aandacht. Dit uiterst belangrijke verschijnsel stond enerzijds in verband met de aristotelische natuurkunde, waarvan het - zoals we later zullen aantonen - één van de meest interessante erfenissen was, en anderzijds met de moderne natuurkunde doordat het de mogelijkheid bood om de tijd te meten. Dit maakte de studie ervan bijzonder interessant in een periode waarin het wateruurwerk en de zandloper weinig betrouwbaar waren, en waarin er geen andere manier bestond om de tijd te meten. Galilei, die hiervoor een beroep moest doen op zijn hartslag, bevestigt dit. De studie van de slingerbeweging, of de meting van de tijd die hierdoor mogelijk werd, werd vanaf dan voor verschillende zaken aangewend, onder meer bij het meten van de geografische lengte - dat, in een periode waarin de scheepvaart in volle ontwikkeling was, door vorsten van verschillende landen werd gestimuleerd.

Dit laatste voert ons naar het domein van het kompas of het magnetisme. Sinds Mercator hoopte men in

[p. 180]

de afwijking van het kompas een middel te hebben gevonden om de geografische lengte te bepalen, maar Stevin had reeds begrepen dat het probleem ingewikkelder was. Sinds 1600 was het magnetisme nauw verbonden met de kosmologie. In die periode toonde Gilbert aan dat de aarde een grote magneet is en beschouwden Kepler, Gilbert en Stevin de krachten tussen de planeten - door ons gravitatiekrachten genoemd - als magnetisch. Deze zienswijze bracht Moretus bijvoorbeeld tot het opstellen van een getijdentheorie. De getijdentheorie vormde reeds het onderwerp van de vierde dag van de Dialogo van Galilei en moest volgens hem als bewijs dienen voor de theorie van Copernicus: ‘Spelenderwijs bewijst de natuur, door middel van het eb en vloed van de zee, de beweging van de aarde’. Dat men genoodzaakt was om op Newton te wachten om een correcte theorie van eb en vloed te hebben, speelt geen enkele rol. Het fenomeen zou trouwens uitgroeien tot een argument in het voordeel van de newtoniaanse theorie.

Ook de optica verdient onze aandacht. Galilei schonk weinig aandacht aan de theorie ervan, maar ze vormt het onderwerp van enkele opmerkingen in de Dialogo, en de optische praktijk leverde de eerste bewijzen van Copernicus' theorie. De hierbij zo bruikbare telescoop was afkomstig uit onze streken, waar auteurs als Stevin en Aguilon de weg bereidden voor de Optics van Newton.

Een andere manier om verbanden te ontdekken tussen verschillende onderzoeksthema's die in een bepaalde periode in de belangstelling stonden, alsook tussen verschillende onderdelen van de kennis, bestaat erin de ordening van deze thema's en kennisonderdelen in handboeken en didactische werken, dit wil zeggen in werken die ondermeer de bedoeling hadden volledig en geordend te zijn, te bestuderen. De manier waarop de auteurs de opbouw van de wetenschap organiseerden, laat toe hun motivaties te achterhalen. We mogen hierbij evenwel niet uit het oog verliezen dat dit hoofdstuk een volledige eeuw bestrijkt en dat de zaken in die tijdsspanne evolueerden.

Laat ons enkele voorbeelden uit het buitenland van naderbij bekijken. Het doel van Galilei in zijn Dialogo is niet zozeer het ordenen van kennis, maar eerder het met alle mogelijke middelen verdedigen van een systeem. Descartes had de ambitie een algemeen systeem op te bouwen dat verslag uitbracht over de ‘natuurfilosofie’ in haar geheel. Huygens en Newton hadden daarentegen de vaste wil een deel van de kennis te structureren en te ordenen. Bij Huygens werd deze kennis nog steeds geleid door de praktijk, maar hij wilde het geheel axiomatisch structureren. Dit wordt bevestigd door zijn brieven. Hierin geeft Huygens toe dat hij zijn theorie over de beweging nooit heeft gepubliceerd omdat hij ze niet axiomatisch heeft kunnen opbouwen. Voor Newton ging het erom gehele takken van de kennis, de dynamica van het punt en de optica, te structureren.

Stevin van zijn kant stond dicht bij de noden van de vorst; we merken dit in zijn studie over vestingen en ‘sterctebou door spilsluysen’ en ook in zijn studie over de toom van paarden. Toch schonk hij ook aandacht aan de statica en de hydrostatica, wat juist wetenschappen zijn die bovengenoemde technische realisaties onderbouwen. Reeds bij Stevin zien we het verlangen om de verschillende takken van de wetenschap te structureren. Elke tak begint met een reeks ‘begheerten’ en iedere stelling wordt op basis daarvan bewezen. Blijft men bij de formele voorstelling, dan blijkt dat Galilei zich vooral toelegt op het overtuigen, terwijl Stevin de nadruk legt op het onweerlegbare van het wiskundig formalisme.

Sommige traktakten lijken nogal overladen omdat de auteurs heen en weer werden getrokken tussen twee polen - enerzijds de verificatie van Copernicus' ideeën en anderzijds de vragen uit de praktijk. In 1634 bijvoorbeeld liet Willem Boelmans door Andreas Tacquet de theses mathematicae, geometricae, arithmeticae, opticae, catopricae, dioptricae, musicae, architectonicae, stereo-staticae, hygrostaticae verdedigen. Deze onderwerpen vormen een typisch geheel van wat in die periode werd behandeld. In de Opera van Tacquet uit 1669 zijn deze onderwerpen nog steeds terug te vinden. In 1640 publiceerde Jan Ciermans een overzicht van de cursus die hij dat jaar gaf. In de bijbehorende kalender, die we hieronder in vertaling weergeven, vermeldt hij per maand de te behandelen materie. Dit laat ons toe de inhoud van zijn onderwijs, de indeling ervan, alsook het verband met bepaalde technische problemen, beter te vatten.

Oktober: Geometrie

1.	De elementen van meetkunde
2.	Over de contact- of raakhoek
3.	Over de instrumenten gebruikt in de geometrie

[p. 181]

November: Aritmetica

1.	Over de verschillende soorten getallen
2.	Het praktisch rekenen
3.	De sinus, tangens, enz.

December: Optica

1.	De perspectief of optische projecties
2.	Stralen weerkaatst door spiegels
3.	Gebroken stralen en de hoeken die ze vormen

Januari: Statica

1.	De vijf krachten, de balans, de hefboom, enz.
2.	Horizontale en schuine bewegingen
3.	De bewegingen veroorzaakt door een intern principe of hulpmiddel

Februari: Hydrostatica

1.	De aard van de vloeistoffen, hun evenwicht, enz.
2.	Over hevels
3.	Over pompen en de stuwing van de vloeistoffen door buizen

Maart: Nautica

1.	Aquaducten, sluizen en andere grote toestellen van dit type
2.	Het schip en zijn onderdelen, het roer
3.	De scheepvaart door middel van een magneet

April: Architectuur

1.	Inwendige verdedigingswerken van steden
2.	Aan de buitenzijde van steden
3.	Uitzonderlijke versterkingen

Mei: Krijgskunst

1.	De legerplaats
2.	De slagorde
3.	De aanval op en de verdediging van steden

Juni: Oorlogstuigen

1.	Het kanonpoeder en de oorlogskatapult
2.	Ballistiek, bogen en oude militaire werktuigen
3.	Bijlage over de zuilen en hun versieringen

Juli: Geografie

1.	De vorm van de wereldbol, zijn grootte, zijn gewicht, enz.
2.	De verschillende manieren om de lengte te bepalen
3.	De aardrijkskundige kaarten

Augustus: Astronomie

1.	De hemelsfeer
2.	Het astrolabium
3.	De loop van de zon en de maan

September: Chronologie

1.	Uurwerken en hun vervaardiging
2.	De maanden en de jaren evenals hun berekening

▪ De optica en de telescoop

De optica was destijds een veelomvattende en erg gevarieerde wetenschap; de werken van Stevin en Aguilon, die aansluiten bij de Dioptrique van Descartes, tonen dit duidelijk aan. Ze hield zich ook bezig met bepaalde problemen uit de Méteores, zoals de regenboog.

De optica omvatte ook de perspectief of scenografie (in dit boek ingedeeld bij de wiskunde) en de projecties (te bespreken in het hoofdstuk over de cartografie). Ze omvatte bovendien al wat te maken heeft met het zien, zowel de samenstelling van het oog (waarover meer in het hoofdstuk over de biologie) als de voorstellingspsychologie, die wil begrijpen hoe beelden door de hersenen worden begrepen. In de door ons besproken periode bewoog de optica zich geleidelijk in de richting waarin we haar nog steeds thuisbrengen, namelijk in die van de dioptrica en de catoptrica, dit wil zeggen de studie van de verschijnselen reflectie en refractie.

Het belang van deze studie groeide, aangezien ze datgene wat men zag door een telescoop geloofwaardig moest maken. Dit bekende instrument is ontstaan in Vlaanderen - al weet men niet precies waar - en heeft zowel Galilei als Gregorius a Sancto Vincentio de mogelijkheid geboden om van naderbij de bewegingen van de sterren te observeren en aldus nieuwe elementen ten gunste van het heliocentrisme, zoals de manen van Jupiter of de schijngestalten van Venus, aan te dragen. Op 4 oktober 1659 schreef Gregorius aan Huygens: ‘Ik heb jouw boek, dat ik snel volledig heb doorgenomen, met veel waardering gelezen. Het doet me terugdenken aan gelijksoortige schijngestalten, die we vijfenveertig jaar geleden voor ons plezier - indien niet gedurende honderden, dan toch in de loop van heel veel nachten - eerst in België, vervolgens in Venetië en tenslotte in Rome observeerden door middel van een telescoop die meester Scholiers aan één van zijn meesters te Antwerpen, pater Odo van Maelcote - die nadien professor in wiskunde werd - had geschonken. Ik kon het moeilijk geloven dat iemand deze ster eerder dan wij, die men de discipelen van Clavius noemde, had ontdekt. We vergeleken de telescoop van Galilei met onze telescopen (en die moesten er zeker niet voor onderdoen) en, in aanwezigheid van Galilei, hebben we aan het Collegium Romanum, voor alle studenten, al deze nieuwe

[p. 182]

Optische experimenten. In: Franciscus Aguilon, Opticorum Libri Sex, Antwerpen, 1613. © B.U.L. ▪

[p. 183]

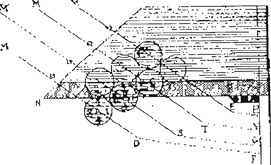
Fig. 1: Ontbinding van het licht zoals beschreven door René Descartes in zijn Dioptrica. Foto uit privé-bezit ▪

fenomenen uiteengezet. We toonden aan dat Venus vanzelfsprekend rond de zon wentelde, wat de filosofen deed mompelen. Bovendien verscheen in die periode, als was het een oor of een handvat, dat wat jij in jouw boek, identificeert als een van de ster gescheiden fenomeen’.

Galilei zelf beaamt in zijn werk dat de telescoop uit Vlaanderen afkomstig is, maar niemand kan met zekerheid zeggen wie hem juist heeft uitgevonden. Het lijkt erop dat het eerder om een Hollandse dan om een Belgische ontdekking gaat. Niettemin publiceerde Charles Malapert in 1620 te Douai een tekst onder de titel Oratio, in qua de novis belgici telescopii phaenomenis non injucunda quaedam academice disputantur.

In mei 1611 woonde Gregorius a Sancto Vincentio aan het Collegium Romanum een zitting bij - onder het voorzitterschap van Odo van Maelcote - waarop Galilei zijn Sidereus Nuncius voorstelde. In dit boek bespreekt Galilei de observaties die hij door middel van een telescoop heeft gedaan. Kort daarop vertelde Gregorius deze gebeurtenis aan de in België achtergebleven van der Straeten. Zijn relaas opent met een voorstelling van het publiek en vervolgt met een samenvatting van de door Galilei in zijn nieuwe werk uiteengezette wetenschappelijke ontdekkingen: ‘Saturnus lijkt ons niet sferisch te zijn, maar een ovale figuur waarvan de grootste diameter parallel loopt aan de equinoctiaal. Jupiter heeft onophoudelijk als satelliet vier planeten die hem steeds vergezellen en voortdurend rondom hem draaien en respectievelijk verschillende posities hebben op verschillende tijdstippen; en toch komen ze steeds in lijn op. Jupiter zelf is altijd volmaakt sferisch. Venus draait steeds rond de zon, net als Mercurius, en hij is er van overtuigd dat het centrum van hun beweging ook het centrum is van de zon; en Venus wordt de nieuwe Cynthia genoemd, want net zoals de maan wast en zakt ze. Wat de vlekken op de maan betreft...’.

De uitvinding van de telescoop gaf een belangrijke impuls aan de studie van de optica, want de tegenstanders van Copernicus wilden niet geloven wat ze door deze verrekijker zagen. Volgens hen ging het om bedrog. Voor de aanhangers van Copernicus was het dan ook van belang de werking van de instrumenten op rationele wijze uit te leggen.

De optica in Stevins Wisconstighe Ghedachtenissen uit 1605-08 had uit drie delen moeten bestaan: t'eerste van de Verschauwing (de perspectief), het tweede vande Beginselen der Spieghelschaeuwen (de catoptrica) en het derde vande Wanschaeuwing, maar zoals Albert Girard reeds heeft onderstreept, is het derde boek nooit gedrukt geworden. In de Beghinselen der Spieghelschauwen bestudeert Stevin de weerkaatsing van lichtstralen op verschillende vormen van spiegels: vlakke, holle en bolle. In essentie komt het erop aan vanuit een vast punt de in een spiegel zichtbare punten te vinden.

Het deel uit Aguilons zes boeken tellend werk uit 1613 over optica dat het nauwst aansluit bij de fysica in de huidige betekenis van het woord werd waarschijnlijk ook door astronomische onderzoekingen geïnspireerd. Het handelt hoofdzakelijk over de verduistering, veroorzaakt door de passage van een donker bolvormig lichaam voor het verlichtend deel van een stralend lichaam. We herkennen hierin duidelijk het zoeken naar een verklaring van eclipsen. Dezelfde bezorgdheid vindt men terug in het deel over optica in het werk van Andreas Tacquet, dat in 1669 - na zijn overlijden - werd gepubliceerd.

Men vindt eveneens een Dioptrica in het reeds vermelde leerboek van Jan Ciermans uit 1640. De opmerkingen van deze laatste ten aanzien van Descartes' theorieën over de kleuren, de regenboog en het fenomeen van de ontbinding van het licht door een prisma, werden door talrijke geschiedkundigen aangehaald. Descartes schreef de kleuren toe aan een verschil in de rotatiesnelheid van de uit een gekleurd voorwerp afkomstige lichtdeeltjes. In de Dioptrica verklaart hij hoe het licht ontbonden wordt wanneer het door een

[p. 184]

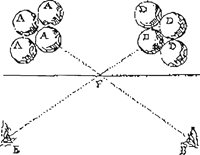
Fig. 2: Elkaar kruisende lichtstralen. Foto uit privé-bezit ▪

prisma wordt gestuurd, met andere woorden hoe de rotatiesnelheden van bepaalde deeltjes in vergelijking met andere worden afgeremd (figuur 1).

In een brief van maart 1638, geadresseerd aan Descartes via Plempius, wijst Ciermans erop dat wanneer twee personen twee gekleurde sterren waarnemen waarvan de stralen elkaar kruisen, zoals voorgesteld op figuur 2, de stralen elkaar zouden moeten beïnvloeden.

Men zou kunnen veronderstellen, merkt Ciermans op, dat de deeltjes elkaar negeren, maar dan begrijpt men niet meer hoe ze zich plotseling van elkaar bewust worden bij de doortocht door een prisma, zoals Descartes het uiteenzette. Bovendien begrijpt men dan niet hoe een deeltje, dat zijn rotatie - ondanks alle hindernissen - vanaf Orion heeft bewaard, deze plots wijzigt bij het verlaten van het prisma.

▪ Statica en architectuur

▫ Kosmologie en statica

Een belangrijk gedeelte van het van Simon Steven is gewijd aan de statica en de hydrostatica. Juist binnen deze domeinen verwierf hij grote roem. De voornaamste resultaten werden verzameld in De Beghinselen der Weeghconst uit 1586. Stevin vernolledigde deze gegevens met een aantal aanvullingen, voor het eerst gepubliceerd tussen 1605 en 1608 in de Wisconstige gedachtenissen. Dit boek bevat alles wat hij tot dat toe had gepubliceerd, aangevuld met enkele nieuwe hoofdstukken.

Net als Galilei had Stevin Belangstelling voor het hellend vlak. Maar meer nog dan Galilei maakte hij een onderscheid tussen statica en dynamica. In zijn werk vinden we dan weer niets over de snelheid. Het bevat daarentegen wel een bewijs van de wet over het gewicht van een lichaam op een hellend vlak. Het gaat hier om de component van de gewichten van een lichaam in de richting van het vlak (figuur 3).

Deze wet werd reeds in de 14de eeuw geformuleerd door de Fransman Jordanus van Nemore, maar Stevin was de eerste om ze te bewijzen. Dit bijzonder originele bewijs doet een beroep op de onmogelijkheid van de eeuwigdurende beweging, die de tegenstelling met de wet in volgende opstelling met zich mee bracht.

Stevin heeft de originaliteit van zijn bewijs goed ingeschat. Daarom heeft hij de figuurlijke voorstelling van dit bewijs op de meeste titelpagina's van zijn latere werken opnieuw afgebeeld. Dit merkteken onderschreef hij met het devies: ‘Wonder en is geen wonder’. Dit devies werd geïnspireerd door de pseudo-Aristoteles die in zijn Mechanica een fundamentele wet uit de ‘statica’ - de wet van de hefboom - probeerde te bewijzen door middel van ‘nog een groter wonder’: de cirkel (figuur 4).

In de toevoegingen uit 1605-08 verschijnen de eerste tekeningen van een andere fundamentele wet uit de mechanica: het krachtenparallellogram (figuur 5).

Zoals men op figuur 3 kan waarnemen, is het gewicht van een lichaam op een hellend vlak een bijzonder geval van deze wet. Het gaat in dit geval om een rechthoek met loodrecht op elkaar staande componenten,

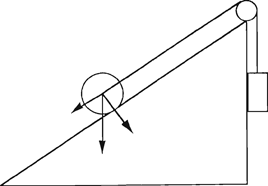
Fig. 3: Lichaam op hellend vlak ▪

[p. 185]

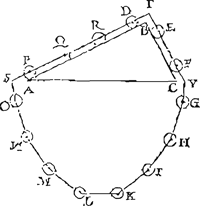
Fig. 4: ‘Mirum non est mirum’. Devies van Simon Stevin, met figuratieve voorstelling van zijn bewijs. Foto uit privé-bezit ▪

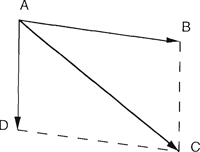
Fig. 5: Krachtenparallellogram ▪

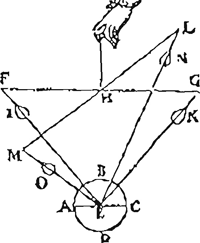
Fig. 6: Weegschaal ▪

vermits de reactie van het vlak er steeds loodrecht op gericht is.

Een ander punt van deze statica toont de originaliteit aan van Stevins denken en onderlijnt de ‘kosmologische’ visie van Stevin en zijn tijdgenoten op bepaalde aspecten van het dagelijkse leven. Deze zienswijze bewijst dat het zoeken naar een bevestiging of weerlegging van de copernicaanse theorie voortdurend in hun gedachten aanwezig was. Men vindt ze ook terug bij iemand als Gregorius a Sancto Vincentio. Stevin onderstelt in zijn statica dat de draden die de gewichten met de weegschaal verbinden parallel zijn. Volgens anderen is dit fout, aangezien de aarde bolvormig is (figuur 6).

Stevins bewering dat ‘overmits dat verschil in alle t'ghene de menschen weghen, onbemerckelick is, want den balck soude al veel milen lanck moeten sijn eer hem dat soude connen openbaren, soo begheeren wij datse voor evenwijdighe ghehouden worden’, wekte de ergernis op van Gregorius a Sancto Vincentio, die dit duidelijk liet blijken in de thesis over de statica die hij in 1624 door Walter van Aelst en Jan Ciermans liet verdedigen.

Uit de titelpagina's van hun publicaties kunnen we afleiden dat deze twee leerlingen twintig stellingen van hun meester moesten verdedigen; de ene in de voormiddag, de andere in de namiddag. Met deze stellingen verwierf Sancto Vincentio enige bekendheid op het terrein van de statica; spijtig genoeg is dit het enige wat we hierover bezitten. Onder Sancto Vincentio's handschriften bevond zich in 1631 een verhandeling over statica van een redelijke omvang. Ze ging echter verloren bij de val van Praag. Enkel zijn wiskundige werken en bovenvermelde stellingen zijn bewaard gebleven.

Net als Galilei - die hij misschien heeft beïnvloed - maakte Sancto Vincentio geen duidelijk onderscheid tussen de statica en de dynamica. Zijn stellingen zijn gewijd aan de beweging van een lichaam op een hellend vlak en vangen aan met een mooie uiteenzetting over het belang dat men moet hechten aan de wrijving. Hierin wordt beschreven hoe men deze wrijving kan verminderen door het contactoppervlak te verkleinen of eventueel te laten verdwijnen; wanneer een bol over een vlak rolt, wordt het oppervlak immers herleid tot een punt. In deze stellingen plaatst Sancto Vincentio Pappus (eind 4de eeuw) tegenover Stevin en levert hij kritiek op deze laatste (figuur 7).

[p. 186]

Volgens Sancto Vincentio is het bewijs van Stevin ongeldig, vermits de bollen niet hetzelfde gewicht hebben op de verschillende hoogten van het hellend vlak. Dit schokt de moderne lezer, die gewend is aan de door Stevin gemaakte benadering over de aan een weegschaal hangende draden. Maar het gaat hier wel degelijk om een benadering en strikt genomen is de bewering vals. De moderne lezer zou zeggen dat g varieert in functie van de hoogte en dat men een benadering maakt wanneer men stelt dat het een constante is, omdat het hoogteverschil niet erg groot is. De vinnigheid van het meningsverschil schemert door in de korte zin onder de afbeelding: ‘Is het verwonderlijk dat de onkundige zich verwondert dat “wonder geen wonder is”’. De strijd zou zich ook na het overlijden van beide hoofdrolspelers voortzetten. Ciermans schreef, nog steeds met betrekking tot hetzelfde bewijs: ‘Ik verwonder me dat dat beroemde wonder, dat helemaal niets afdoet aan de oorzaak van de bewondering, ermee zou ophouden een wonder te zijn’.

Sancto Vincentio verkoos het gewicht van een lichaam op een hellend vlak te vinden door middel van de wet van de hefboom. Hij deelde hiermee de mening van Galileo Galilei en Gilles de Roberval (1602-1675), die in 1636 een uitgebreid artikel publiceerde onder de titel Traité de mechanique des poids soustenus par des puissances sur les pans inclinez à l'horizon. Deze gedachte bracht Gregorius op een nieuw idee om de kwadratuur van de cirkel - die hem nauw aan het hart lag - te berekenen. In de correspondentie van zijn leerlingen Theodoor Moretus en Gilles-François de Gottignies vinden we inderdaad een discussie over dit onderwerp. Sancto Vincentio's idee komt ook voor in de geschriften van Leonardo da Vinci (1452-1519). Ze hield in dat een lensvormig

Walter van Aelst, Theoremata mathematica scientiae staticae. De ductu ponderum per planitiem recta & oblique horizontem decussantem, 1624. Verdediging van de stellingen van Gregorius a Sancto Vincentio. Foto uit privé-bezit ▪

[p. 187]

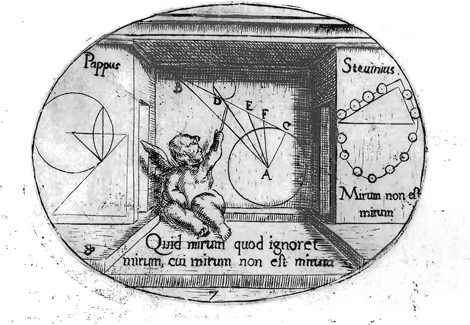
Fig. 7: Gregorius a Sancto Vincentio plaatst de stellingen van Pappus tegenover die van Stevin. Afbeelding uil het werk van Walter van Aelst, 1624. Foto uit privé-bezit ▪

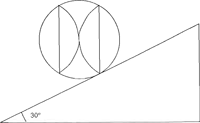
Fig. 8: Schema bij het bewijs van Goltignies ▪

deel van de bol door het vlak werd gedragen, terwijl het andere deel het gewicht in zijn val meevoerde en dus een tegengewicht noodzakelijk maakte. Moretus verdedigt in zijn brieven de opvatting dat de zwaarte van het tegengewicht toelaat het volume van de in evenwicht gehouden bolsector vast te stellen. Deze stelling werd - met reden - door Gottignies bestreden. We kunnen dit illustreren met een eenvoudig tegenvoorbeeld. Bij een hoek van 30^o moet het tegengewicht de helft van het gewicht wegen en moet de dikte van het maantje de helft van de straal bedragen, zoals in figuur 8 - die de fout aantoont - is voorgesteld.

Het is nochtans mogelijk dat de bezwaren van Gregorius a Sancto Vincentio aan het adres van Stevin van een gans andere orde zijn. In zijn stellingen uit 1640 zegt Ciermans: ‘Daarenboven is de verhouding die wij hebben toegekend aan de gewichten die zich op hellende vlakken bevinden, niet alleen geldig voor vlakken, maar voor om het even welk oppervlak dat schuin is ten opzichte van de horizon. De wet is dus ook van toepassing op spiralen en kronkelende lijnen, verstrengeld met parallellepipeda, piramiden en kegels’. Het bewijs van Stevin laat inderdaad niet onmiddellijk toe er andere eenvoudige werktuigen, zoals de schroef, de katrol, de wig, enz. uit af te leiden, zoals de pseudo-Aristoteles dat deed vanuit de hefboom. Dit probleem, dat erin bestaat de toenmalige statica - dit is de studie van eenvoudige werktuigen - te axiomatiseren, wordt eveneens aangesneden in een onafgewerkt handschrift van Jacques-Honoré Durand (ca. 1598-1644), getiteld Machina Mathematice et Physice demonstrata; seu Tractatus, in quo Machinae, ad certam, universalem,

[p. 188]

Gebouwen van de jezuïeten te Antwerpen. Gravure, 17de eeuw. Foto uit privé-bezit ▪

et omnibus communem regulam, et causam Physicam continentem reducuntur. De axiomatische bijklank is in dit werk, dat eveneens ontsproten is uit dat van de pseudo-Aristoteles, duidelijk waarneembaar. Het komt er op aan de studie van het geheel van eenvoudige werktuigen terug te brengen tot één enkel fundamenteel principe. De pseudo-Aristoteles en al diegenen die hem gedurende meer dan duizend jaar volgden, herleidden deze werktuigen tot de hefboom. Pas in 1687, na het overlijden van de hier besproken hoofdrolspelers, zou Pierre Varignon (1654-1722) deze idee overhoop gooien, door dezelfde kennis te funderen op de wet van het krachtenparallellogram.

Om deze paragraaf te beëindigen, nog een woordje over het onderzoek met betrekking tot het zwaartepunt. Dit onderzoek vindt men terug in talrijke werken, bijvoorbeeld in die van Jan-Karel della Faille, Tacquet en anderen, maar de strekking ervan is eerder wiskundig dan natuurkundig. Het natuurkundig begrip van het zwaartepunt werd over het algemeen niet in vraag gesteld, maar wel de wiskundige methoden die ons in staat moeten stellen het zwaartepunt te bepalen. We verwijzen de lezer dus naar het hoofdstuk over de wiskunde.

▫ Architectuur en vestingbouw

In de hier behandelde periode ontstaat geleidelijk het onderscheid tussen vestingbouw en architectuur. Stevin wijdde enkele vooral beschrijvende geschriften aan vestingbouw en ‘castrametatio’ of legermeting, dat is de beschrijving van de bouw en inrichting van een legerkamp. Deze zuiver op de oorlog gerichte wetenschappen werden, zoals hij aankondigt, bedreven door ‘Tres-puissants Seigneurs, Messeigneurs les Estats’. Ciermans besteedde in zijn lessen één maand aan de architectuur, maar ook hier was er enkel sprake van militaire bouwkunst of versterkingen.

We weten nochtans dat Aguilon, Gregorius a Sancto Vincentio en hun school zich ten dienste van de Kerk

[p. 189]

en de Contrareformatie hebben gesteld om enkele van onze mooiste barokkerken te bouwen. Het is vreemd, maar misschien typisch voor België of voor de jezuïetengemeenschap, te zien hoe allen die de wiskunde of de statica in deze school hebben bestudeerd, in verband kunnen worden gebracht met grote bouwkundige projecten. Deze band met de statica wordt door Ciermans aan het begin van zijn lessen over de architectuur geformuleerd: ‘We verbinden de architectuur met elementen uit de statica’.

Dat een vorst voor zijn ingenieurswerken een beroep doet op een wetenschapper van het kaliber van Simon Stevin is altijd al gebruikelijk geweest, maar dat de

Franciscus Aguilon, Opticorum Libri Sex, Antwerpen, 1613. © B.U.L. ▪

Portret van Wensel Cobergher.
In: Isaac Bullart, Académie des Sciences et des Arts, Brussel, 1695. © B.U.L. ▪

meeste leerlingen van een school tegelijk leermeester in de wiskunde én de architectuur worden, is eerder ongewoon. In het Belgische geval echter volgde een ganse school het voorbeeld van hun eerste meester in deze materie, Franciscus Aguilon.

Laatstgenoemde heeft samen met Pieter Huyssens (1577-1637) de jezuïetenkerk te Douai en de Sint-Carolus Borromeuskerk te Antwerpen gebouwd; waarschijnlijk kregen ze hulp van Pieter-Paul Rubens (1577-1640) en misschien ook van Wensel Cobergher (1560-1634). De betrekkingen tussen Aguilon en de grote kunstschilder zijn overigens bekend; de prachtige gravure op de voorpagina van de Optica van Aguilon wordt aan hem toegeschreven.

De kerk van Maastricht (1614), Sint-Walburga te Brugge (1619), de jezuïetenkerk van Saint-Loup te Namen (1621) en de Onze-Lieve-Vrouwekerk van Sint-Pieter te Gent (in opdracht van de benedictijnen van de Blandijnberg op het Sint-Pietersplein) staan eveneens op naam van Pieter Huyssens.

Gregorius a Sancto Vincentio kwam op dit vlak in botsing met één van zijn jongere collega's, Willem

[p. 190]

Hesius (1542-1613), leermeester van Tacquet en ontwerper van de plannen van de Sint-Michielskerk in Leuven (1650-66) en de karmelietenkerk in Brussel. In 1658 had Gregorius de plannen getekend voor het jezuïetencollege van Gent en deze plannen waren goedgekeurd door de generaal van de orde, Goswino Nickel. Maar Hesius, die er zelf andere had gemaakt, was op dat moment rector van het college geworden. Hesius liet zijn eigen ontwerpen uitvoeren en werd hiervoor berispt door de generaal. Indien we Gilissen mogen geloven, dan zou Gregorius a Sancto Vincentio ook in Praag (1626-1637) voor de renovatie van het college zijn aangezocht.

Andere leerlingen uit deze school, zoals Willem Boelmans, Jan Ciermans en Andreas Tacquet hielden zich eveneens met architectuur bezig.

Hydrostatica en sluizen

In 1585 beschreef Simon Stevin voor de eerste maal de macht der drucking des waters teghen bodems. De beschrijving van de druk van het water op de bodem van een vat luidt als volgt: ‘Op yder bodem des waters evewijdich sijnde vanden sichteinder, rust een ghewicht even ande swaerheyt waters die evegroot is met den pijlaer, wiens grondt dien bodem is, ende hoochde, de hangende lini van 't plat door 't waters oppervlack tot den gront’. In dezelfde tekst toont hij aan dat de druk in alle richtingen gelijk blijft.

Naast zijn verhandeling over de vestingbouw op basis van de statica, stelde Stevin een verhandeling over de versterking door middel van sluizen, met daarin een beschrijving van een nieuw type sluisdeuren. De lesnota's van Jan Ciermans sluiten aan bij Stevin: de hydrostatica wordt gevolgd door de nautica, waarvan het eerste deel gewijd is aan aquaducten en sluizen (zie tabel p. 181); daarna komen krijgskunde en vestingbouw. Hoewel Ciermans' lesnota's getuigen van het feit dat de hydrostatica deel uitmaakte van zijn cursus, kent men van hem geen publicatie over dit onderwerp.

▪ De bewegingsleer

De bewegingsleer die zou uitmonden in onze dynamica vormde waarschijnlijk nog geen onderdeel van cursussen voor studenten, aangezien ze in de lesnota's van Ciermans niet aan bod komt. Toch hielden onderzoekers er zich mee bezig, enerzijds bij het bestuderen van het - voor die periode - centrale probleem van de botsingen, anderzijds bij het behandelen van het bekende probleem van de val van een lichaam.

▫ De botsingen

Het belang van botsingen bij de verklaring van de wereld zoals voorgesteld door Descartes laat zich al voorspellen uit wat reeds over de optica werd gezegd. In zijn Principia philosophiae kent Descartes een fundamentele plaats toe aan de botsingswetten. Ze volgen onmiddellijk op de wet van het behoud van de bewegingshoeveelheid, waaruit ze trouwens zijn afgeleid. Spijtig genoeg zijn zowel de door Descartes geformuleerde wet van behoud van de bewegingshoeveelheid als de botsingswetten die hij daaruit afleidt volledig fout. Descartes hield immers geen rekening met het vectoriële aspect van de snelheid, dat in de hoeveelheid van beweging voorkomt en waardoor twee hoeveelheden van beweging elkaar kunnen versterken of opheffen, naargelang hun snelheden tegengesteld zijn ofwel dezelfde richting volgen. Huygens, leerling van Descartes, zou deze ideeën verbeteren door het behoud van de hoeveelheid van beweging op een juiste manier uit te leggen en eveneens door de wet van het behoud van energie toe te passen om de botsingswetten te vinden. Zijn ideeën kregen vorm in de periode dat hij over dit onderwerp correspondeerde met René-François de Sluse. Hiervan getuigen het eerste uit 1656 daterende handschrift met als titel De motu corporum ex percussione en de aan de Royal Society toegestuurde versie van de botsingswetten uit 1669. Sluse heeft zeer goed het fundamentele karakter van de botsingswetten en van de wet van behoud van bewegingshoeveelheid voor Descartes begrepen, daar hij op 18 december 1657 aan Huygens schreef: ‘Indien het principe van Descartes betreffende de hoeveelheid van beweging welke constant blijft in het universum, niet langer houdbaar is, komen alle fundamenten van zijn filosofie op de helling te staan’.

Beide mannen waren het erover eens dat de botsingswetten van Descartes fout waren. Ze vergeleken elkaars bevindingen in een briefwisseling, die gespreid ligt over de jaren 1657 en 1658; dit wil zeggen vóór de prijsvraag van de Royal Society. De prijsvraag die Oldenburg op 5 november 1668 in naam van de Royal Society aan Huygens stelde, laat ons toe te achterhalen hoe belangrijk botsingsverschijnselen in die tijd werden geacht. Inderdaad, op de vraag: wat zijn ‘de aard

[p. 191]

en de wetten van de beweging’, werd zowel door Christiaan Huygens als door John Wallis (1616-1703) en Christopher Wren (1632-1723) geantwoord met een behandeling van de botsingswetten. Voor hen ging het dus om de grondslag van de dynamica. Wallis en Wren hebben de wet van de niet-elastische botsing gevonden, terwijl Huygens de wet van de elastische botsing heeft voorgesteld. Hierbij merken we op dat Wren diegene is die de Londense Saint Paul's Cathedral heeft ontworpen.

▫ De val van een lichaam en de ballistiek

Een ander belangrijk element in de reeds vermelde stellingen van Gregorius a Sancto Vincentio over de statica, vormt de studie van de val van een lichaam. Hij behandelt vooreerst een lichaam dat daalt langs een hellend vlak, vervolgens op een reeks van dergelijke vlakken en tenslotte op een reeks steeds kleiner wordende hellende vlakken (waterdruppels) en hij beschrijft de beweging van een waterval die - hoewel hij dit niet expliciet zegt - volstrekt parabolisch is.

In zijn besluit bevestigt Sancto Vincentio dat de twee bewegingen waaraan vallende lichamen onderworpen zijn, namelijk de beweging die ze hebben verkregen door over een hellend vlak te rollen én het effect dat wordt veroorzaakt door het gewicht, zich onafhankelijk van elkaar voordoen. In meer moderne bewoordingen komt het er op neer dat de zwaarte-

Beweging van een waterval. In: Walter van Aelst, Theoremata..., 1624. Foto uit privé-bezit ▪

kracht en de inertie onafhankelijk van elkaar bestaan. Men moet hierbij opmerken dat Sancto Vincentio in tegenstelling tot Galilei geen besef had van de inertie, maar zijn opmerking over de onafhankelijkheid van beide krachten was fundamenteel voor de redenering waarmee Galilei de parabolische wet van de val heeft opgebouwd. Het is niet uitgesloten dat Galilei zich door Sancto Vincentio heeft laten beïnvloeden. Beide mannen hebben elkaar te Rome ontmoet in mei 1611 en de uitwisseling van wetenschappelijke informatie tussen Italië en België verliep erg vlot.

Monchamp en Le Paige wezen er op dat verschillende Belgen zich met dit probleem hebben beziggehouden, onder andere Govaart Wendelen (1580-1667) en Ignace Der Kennis (1598-1656). In 1642 deed Léandre Brandt enkele experimenten en in 1644 publiceerde Jean Caramuel de Lobkowitz (1606-1682) te Leuven een Perpendiculorum inconstantia et Sublimium ingeniorum crux, sive de lapsu gravium.

▪ Het magnetisme en de zee

Onder invloed van Gilbert was Simon Stevin - overigens net als Kepler - van mening dat de krachten die worden uitgeoefend op planeten magnetische krachten zijn. Dit verklaart ongetwijfeld gedeeltelijk waarom men toentertijd zoveel belang hechtte aan de studie van magnetische verschijnselen. Verschillende Belgische auteurs getuigen van deze belangstelling: bijvoorbeeld Jean Tasnier, die delen vertaalde uit de bekende Epistola de Magnete van Petrus Peregrinus, en de minder bekende Gaspar van Baerle (1584-1648), die in 1600 de Observations ou expériences magnétiques de la Terre publiceerde.

Ook op dit terrein vermengde de kosmologische probleemstelling zich met op de praktijk gerichte imperatieven. In de periode waarin de grote zeereizen meer en meer tot ontwikkeling kwamen, stond het probleem van de plaatsbepaling op zee of van de bepaling van de lengte centraal en probeerde men de getijdenwerking beter te begrijpen. Daar het bepalen van de lengte eveneens kon herleid worden tot een juiste tijdmeting zijn ook studies over de slingerbeweging tot ons gekomen.

▫ Magnetisme en het bepalen van de lengte

Tussen 1541 en 1551 had Gerard Mercator - nog steeds in een precopernicaanse context - een nieuwe werkwijze voorgesteld die zeelieden in staat moest

[p. 192]

Ballistische berekeningen.
In: Levinus Hulsius, Tractatus Primus Instrumentorum mechanicorum, Frankfort, 1605. © B.U.L. ▪

stellen hun plaats op zee te bepalen, dankzij het opmeten van de magnetische afwijking en enkele relaties uit de boldriehoeksmeting. Mercator vereenvoudigde het probleem door een magnetisch eiland te onderstellen, gesitueerd in de noordelijke poolstreek. Zijn magnetische meridianen zijn grote cirkels die door de pool gaan, wat neerkomt op de onderstelling dat de magnetische polen diametraal tegenover elkaar staan. Daar is niets van waar en alhoewel de idee van Mercator waardevol was, was de uitvoering ervan zeer ingewikkeld. Niettemin staken eerst Petrus Plancius en Simon Stevin, vervolgens de orde der jezuïeten, onder leiding van Kircher en Ricciolli, van wal om op verschillende plaatsen en tijdstippen de magnetische afwijking op te nemen of te laten opnemen. Het doel was een kaart waarop de lijnen van dezelfde afwijking werden weergegeven en die de mogelijkheid bood zich beter te situeren. Een dergelijke kaart zou uiteindelijk in 1705 door Edmund Halley (1656-1742) worden gepubliceerd.

Om dit doel te bereiken, deed Riccioli een beroep op ‘alle geschoolde broeders uit onze sociëteit om tijdens hun zeereizen naar West- of Oost-Indië of naar Nieuw-Frankrijk waarnemingen op te tekenen en deze te verzenden naar de broeders Kircher, Scheiner, Grienberger of onszelf’. Kircher en hij publiceerden tafels met de resultaten van deze opmetingen en de namen van diegenen die ze hadden uitgevoerd. Op deze tafels leze men de namen van enkele Belgen, onder wie Gregorius a Sancto Vincentio en Jan Ciermans. Michiel Coignet en Michel-Florent van Langren werden evenwel niet vermeld, hoewel ook zij over dit onderwerp hadden gepubliceerd. Laatstgenoemden waren echter geen jezuïeten.

De katholieke koningen - een omschrijving van Michel-Florent van Langren ter aanduiding van de koningen van Spanje en Portugal - hadden een aanzienlijke beloning in het vooruitzicht gesteld voor diegene die een methode zou vinden voor het bepalen van de lengte. De methode die van Langren, met de medewerking van Jan-Karel della Faille, hen voorstelde, kwam misschien uit dezelfde hoek. In de gepubliceerde tekst is de geleverde methode spijtig genoeg gecodeerd en dus onleesbaar.

[p. 193]

▫ Magnetisme en de getijden

Zoals Stevin aankondigt in zijn eerste ‘begheerte’ met betrekking tot de getijden, ‘bevint men deur daghelieksche gheduerighe ervaringen, dat ebbe en vloet van de Maan gheregiert worden’. Volgens hem worden de getijden veroorzaakt door een ‘trecking’ of ‘suyging’ van de maan. Hij voorziet eveneens de mogelijkheid van een ‘persing’, die aanleiding zou geven tot hetzelfde verschijnsel. Nochtans weigert Stevin zich verder te wagen wanneer het gaat over de oorzaken hiervan, ‘doch anghesien t'vermoen van ettelieke is, t'selve deur de voorschreven suyging te geschien, so is

Fig. 9: Schema bij de redenering van Gregorius a Sancto Vincentio ▪

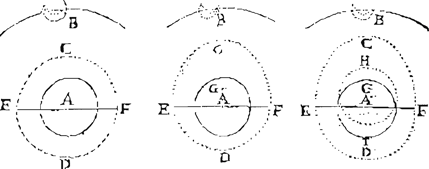
Fig. 10: Getijdentheorie. Theodoor Moretus, Tractatus physicomathematicus de aestu maris. Foto uit privé-bezit ▪

dat wy begheeren sulcx toegelaten te worden, om also ons voorghenomen spiegheling een gront te gheven’.

Gregorius a Sancto Vincentio schreef de getijden toe aan een draaiing van de aarde. In één van de weinige handschriften die niet uitsluitend over de wiskunde handelen en dat berust in de Koninklijke Bibliotheek van België, toont hij aan dat het zwaartepunt van de aarde verschoven is en dat de terugkeer van dit centrum naar zijn aanvankelijke positie een beweging van het water veroorzaakt (figuur 9).

In 1640 maakte Ludovico de Schildere (1606-1667) een zeer bondig verslag van een theorie van dit type. De eerste die een volledige publicatie aan dit onderwerp wijdde was Theodoor Moretus (1602-1667) in 1665. In zijn werk formuleert hij eerst enkele algemeenheden over magneten en vermeldt hij terzijde dat Jacques-Honoré Durand de magnetisering heeft waargenomen van ijzeren staven uit het traliewerk van een venster. Deze staven hadden gedurende een lange tijd in dezelfde verticale positie gestaan, en waren - zoals we heden ten dage weten - gemagnetiseerd door het magnetisch veld van de aarde. Durand is waarschijnlijk onafhankelijk van le Lorrain de Vallemont, die in 1651 Description de l'aimant qui s'est formé à la pointe du clocher de notre Dame de Chartres publiceerde, tot deze vaststelling gekomen.

[p. 194]

Moretus vervolgt zijn tekst met de vaststelling dat de magnetisering gebeurde zonder aanraking van een ijzeren naald, dit is wat wij de magnetisering door inductie zouden noemen. In beide gevallen gaat het om een waarneming van merkwaardige verschijnselen waarvoor de auteur geen verklaring geeft. Dit zou pas honderd jaar later gebeuren.

Net als Gilbert bevestigt Theodoor Moretus in zijn Tractatus physico-mathematicus de aestu maris dat de aarde één grote magneet is en volgt hij de idee van zijn meester Gregorius a Sancto Vincentio. Hij verklaart het fenomeen van de getijden door middel van de magnetische aantrekkingskracht van de maan. De maan trekt de aarde aan en vervormt haar, waardoor het zwaartepunt wordt verschoven, wat dan weer een beweging van de zeeën veroorzaakt. Om de theorie van Moretus op punt te stellen zou het volstaan magnetische aantrekkingskracht te vervangen door gravitatiekracht.

Fig. 11: Spiraalbeweging. In: Walter van Aelst, Theoremata...,1624. Foto uit privé-bezit ▪

▫ Meting van de tijd, de slinger en lengtecirkels

Het bijzondere aan de hiervoor vermelde stellingen van Gregorius a Sancto Vincentio over de statica, ligt in de uitwerking van het theorema over het behoud van energie. De tekst van Gregorius stelt ons in staat de redenering te achterhalen die hem tot daar heeft geleid en die moet worden toegeschreven aan verschillende andere auteurs. Aristoteles, gevolgd door Albert van Saksen in de Middeleeuwen, veronderstelde dat het centrum van de aarde - dat ook het centrum van de wereld was - zich bevond op de plaats waar de zware lichamen zich naartoe begaven, indien ze niet tegengehouden werden door een steun, zoals Leonardo da Vinci beweerde. Bijgevolg moet men een inspanning doen - in moderne termen heet dit gebruikmaken van energie - om een zwaar lichaam uit het centrum van de aarde te verwijderen. In de tekst van Sancto Vincentio lezen we dat de belangrijke grootheid in deze context de verhoging van de afstand is ten opzichte van het middelpunt van de aarde, dit wil zeggen, de hoogte tot waar men het voorwerp opheft. Omgekeerd,

[p. 195]

Fig. 12: Slingerbeweging.
In: Walter van Aelst, Theoremata...,1624. Foto uit privé-bezit ▪

indien men een voorwerp laat vallen, is de opgestapelde energie enkel afhankelijk van de hoogte die het heeft overbrugd. Gregorius a Sancto Vincentio verklaart dit door als voorbeeld een ingewikkelde spiraal te nemen, die merkwaardig genoeg sterke gelijkenissen vertoont met die van San Ivo, welke nochtans van latere datum is.

Hij beweert met reden dat de kogel die langsheen deze spiraal afdaalt, evenveel energie krijgt als diegene die onmiddellijk verticaal naar beneden gaat. Galilei uit dezelfde bewering ten aanzien van een kogel die afdaalt op een hellend vlak, maar een dergelijke kronkelende afdaling wordt door hem niet in beschouwing genomen. Sancto Vincentio beseft dat men zo'n baan kan terugbrengen tot een opeenvolging van hellende vlakken.

De auteur werkt zijn redenering verder uit. Aangezien de oorzaak van de opgestapelde energie of de noodzakelijkheid energie te leveren, hetzelfde blijft bij verwijdering of nadering van het centrum van de wereld, zal deze energie behouden blijven. Vandaar dat een slinger na een neerwaartse beweging naar de ene zijde, steeds opnieuw tot dezelfde hoogte opklimt aan de andere zijde, terwijl de wrijving - zoals Sancto Vincentio nadrukkelijk heeft onderstreept - verwaarloosd kan worden. Sancto Vincentio heeft deze ontdekking met talrijke voorbeelden geïllustreerd.

Andere Belgische auteurs zoals Godfried Wendelen en Jan-Karel della Faille bestudeerden eveneens de slingerbeweging, en dit om andere redenen. Zo leren we uit de briefwisseling tussen Michel-Florent van Langren en Jan-Karel della Faille dat dit het onderwerp was van een studie in de - momenteel onvindbare - stellingen die della Faille in 1625 te Dôle publiceerde. We weten ook welke belangrijke rol de slingerbeweging heeft gespeeld bij Galilei's redeneringen. In het kader van zijn astronomisch onderzoek gebruikte Wendelen, in navolging van Galilei, de slinger om de tijd te meten. Dit bracht hem ertoe op proefondervindelijke wijze het isochronisme van laatstgenoemde te verifiëren. Hiervoor vergeleek hij enerzijds

[p. 196]

de schommelingen in functie van de amplitude van de vertrekhoek en analyseerde hij anderzijds het verband tussen de laatste schommelingen (de tien laatste graden). Caramuel de Lobkowitz verzette zich tegen Gassendi in een kort geschrift, waarin hij de bestendigheid van de slingerbeweging bevestigt, of juister, waarin hij stelt dat deze beweging niet beïnvloed wordt door de beweging van de aarde. Nogmaals zien we hier de vermenging van aardse natuurkunde en kosmologie.

▪ Besluit

Het is best mogelijk de 17de-eeuwse natuurkunde te laten uiteenvallen in een groot aantal uiteenlopende problemen, zoals reflectie en refractie, de val van een lichaam, de slingerbeweging, het probleem van de lengte, en vele andere. Nochtans is het ook mogelijk haar eenheid te beschrijven, door enerzijds de banden met de meer praktische problemen uit die tijd - zoals de navigatie en de vestingbouw - in beschouwing te nemen en anderzijds door melding te maken van de gevolgen van de copernicaanse revolutie, die zich binnen dit domein - meer dan binnen enig ander - sterk heeft laten voelen.