Geschiedenis van de wetenschappen in België van de Oudheid tot 1815

[p. 27]

Robert Halleux
De Lotharingse wiskundeschool en de opkomst van de Arabisch-Latijnse wetenschap in de 11de en de 12de eeuw

Een belangrijk breukpunt in de geschiedenis van de middeleeuwse wetenschap vormt de invoering van nieuwe kennis door middel van Latijnse vertalingen uit het Arabisch. Hoe onze gewesten deze kentering hebben ervaren is een vraag die reeds herhaaldelijk is gesteld, maar tot op heden slechts gedeeltelijk werd beantwoord. Men stuit immers steeds op een aantal problemen van geografische, chronologische en conceptuele aard.

De provincies van de huidige staat België vormen het noordwestelijke deel van Lotharingen, dat in de besproken periode moet worden beschouwd als een volwaardige culturele ruimte. In de 11de eeuw bestond er een typisch Lotharingse wetenschap, met een eigen inhoud en eigen geleerden.

Vanuit chronologisch standpunt onderscheiden de historici meerdere fasen: vooreerst een fase waarin de nieuwe wetenschap langzaam doorsijpelde (10de-

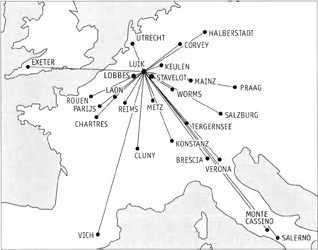
Invloed van de Maaslandse scholen in Europa, 10de-12de eeuw. ©C.H.S.T. ▪

11de eeuw), met Gerbert van Aurillac (ca. 940-1003) en Constantinus Africanus (fl.1065-1085) als meest opmerkelijke figuren; vervolgens een fase van intensieve vertalingen (12de eeuw), met Spanje en Zuid-Italië als voornaamste centra; tenslotte een laatste golf van vertalingen die hoofdzakelijk tot stand kwamen aan het Zuid-Italiaanse hof van de prinsen van Anjou (13de eeuw).

Vanuit thematisch standpunt staat het vast dat de nieuwe wetenschap het kader van de toenmalige kennis volledig heeft opengebroken. Het is van belang de nieuwe thema's die in het quadrivium werden opgenomen, te onderscheiden van de kennis die niet tot het quadrivium behoorde en de structurele verschuivingen die binnen het quadrivium zelf plaatsvonden.

▪ De 11de eeuw

De wiskundeschool die tussen het midden van de 10de en het midden van de 11de eeuw in Lotharingen actief was, werkte binnen het ruime kader van het quadrivium en had als centrum de stad Luik. De geleerden en werken die deze school heeft voortgebracht, behoren tot twee verschillende generaties.

Een eerste generatie van wiskundigen wordt in verband gebracht met de school van Reims, waar Gerbert de leiding over het onderwijs op zich had genomen. Notger, bisschop van Luik tussen 972 en 1008, is mogelijk de auteur van een ‘scholium’ bij de Arithmetica van Boëthius. Zijn medewerker Heriger, abt van Lobbes (vóór 950-1007), schreef de Regulae numerorum super abacum Gerberti, dit zijn regels voor het rekenen met een rekenbord. Adelbold (ca. 960-1027), die te Lobbes en te Luik had gestudeerd en bisschop werd van Utrecht, correspondeerde met Gerbert over het oppervlak van een gelijkzijdige driehoek en over de inhoud van een bol. Hij schreef ook een commentaar op een over aritmetica handelende passage uit De consolatione philosophiae van

[p. 28]

Boëthius. Hoewel geen van deze auteurs een rechtstreekse discipel was van Gerbert, was hun werkwijze gelijklopend.

Tot de tweede generatie geleerden, die onder impuls van Fulbert (950-1028) haar vorming kreeg te Chartres, behoren Radulf en Ragimbold, respectievelijk leraar te Luik en scholaster te Keulen en bekend omwille van de briefwisseling die zij tussen 1020 en 1027 met elkaar onderhielden, en Franco van Luik, die omstreeks 1050 in samenwerking met Falchalinus, scholaster van Saint-Laurent, De quadratura circuli schreef. Door indirecte overlevering weten we dat ook andere scholasters, zoals Wazon (ca. 985-1048), Adelman (ca. 1000-1061) en Razechin zich met de mathematica hebben beziggehouden; spijtig genoeg zijn haast al hun geschriften verloren gegaan.

Aan de Lotharingse school kunnen tevens een aantal anonieme teksten worden toegeschreven: de Geometria incerti auctoris, door Nicolaus Bubnov uitgegeven in het verzameld werk van Gerbert; een verhandeling De triangulis, opgenomen in een handschrift uit het hospitaal van Cues, waarin een oplossing wordt gegeven voor de problemen die door Radulf en Ragimbold werden geformuleerd; de apocriefe Geometria II van Boëthius, die volgens Menso Folkerts van Lotharingse en volgens Paul Butzer van Luikse oorsprong is.

Een homogeen netwerk van geleerden en handschriften strekte zich over heel Lotharingen uit: Notger was afkomstig uit Sankt Gallen, Adelbold week uit van Luik naar Utrecht, Adelman van Luik trok naar Duitsland, Radulf correspondeerde vanuit Luik met Ragimbold in Keulen, Franco droeg zijn De quadratura op aan Herman II van Keulen (†1056), Herman de Lamme (1013-1054), monnik te Reichenau en leerling van Berno van Prüm (†1048) had als discipel Meinzo van Konstanz.

Bijkomende argumenten voor deze homogeniteit worden aangevoerd door de handschriften zelf. De handschriften van de Geometria II vonden bijvoorbeeld hun oorsprong in Lotharingen en in de bijhorende invloedssfeer (Trier, Toul, Verdun, enz.). Ze bevatten eveneens teksten van andere wiskundigen die tot de Lotharingse school behoren, de bronnen die door hen werden geraadpleegd en teksten die, hoewel nauw aan elkaar verwant, van elders afkomstig zijn (Chartres, Reichenau). De manuscripten dateren voor het merendeel uit de 11de en de 12de eeuw; in de 13de eeuw had immers niemand meer belangstelling voor deze vorm van wiskunde.

Voor de voornaamste takken van het quadrivium - geometrie, aritmetica en astronomie - is het van belang de wetenschappelijke inhoud van de belangrijkste werken te onderzoeken en er eventuele sporen van Arabisch-Latijnse wiskunde in aan te wijzen. Attestaties over rechtstreekse contacten met het Arabische deel van Spanje zijn eerder zeldzaam. Johannes van Gorze verbleef tussen 954 en 956 aan het hof van Abd-er Rahman III (r. 912-961) te Cordoba; diens vertrouweling Racemund verbleef op zijn beurt gedurende acht maanden in Gorze, meer bepaald tussen 955 en 956. Deze aanwezigheid lijkt zich niet te hebben vertaald in een wetenschappelijke bijdrage aan de bibliotheek van Gorze. In 1056 trokken enkele Luikse pelgrims, onder leiding van een monnik uit de abdij van Saint-Jacques, naar Compostella. Bij hun terugkeer hadden

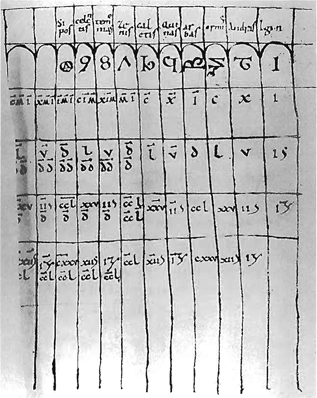
Arabische cijfers in een Geometria II-handschrift van ‘Boëthius’. Erlangen, Hs. 379 f. 35 r^o. © C.H.S.T. ▪

[p. 29]

Geniëlleerd zilveren doosje met Arabische opschriften, 11de-12de eeuw. Luik, Musée Curtius. © C.A.L. ▪

ze relieken bij van Sint-Jacob en van andere heiligen. Het is onzeker of het geniëlleerd zilveren doosje, dat nog steeds te Luik wordt bewaard en dat bekrast is met Arabische inscripties uit de 11de en de 12de eeuw, een getuige is van deze pelgrimstocht.

Teneinde de invloed vast te stellen die de wetenschappelijke school van Lotharingen heeft ondergaan, zullen we drie takken van het quadrivium van naderbij bekijken: de geometrie, de aritmetica en de astronomie. Dit onderzoek valt uiteen in twee delen: vooreerst een analyse van de inhoud van de belangrijkste werken en vervolgens een benadering van de bronnen die de auteurs hebben geraadpleegd.

▫ Geometrie

Analyse van de belangrijkste werken

Brief van Adelbold aan Gerbert over de manier waarop men de inhoud van een bol berekent

Deze brief werd geschreven toen Gerbert reeds tot paus was verkozen (999-1003). Adelbold was op dat moment nog erg jong. In de brief verontschuldigt hij zich immers bij Gerbert omdat hij, als jonge man, zich tot hem richt als een collega. Toen Macrobius in zijn In somnium Scipionis de omvang van de sterren besprak, stelde hij dat een bol waarvan de diameter dubbel zo groot is als die van een andere bol, een volume (‘crassitudo’) heeft dat het achtvoudige bedraagt van dat van de andere bol. Om dit te begrijpen moet men volgens Adelbold de inhoud van de bol berekenen. De omtrek [2ΠR] wordt verkregen door de diameter te vermenigvuldigen met 3 1/7, wat aan Π de waarde geeft van 3 1/7, het oppervlak [ΠR²] door de helft van de diameter [R] te vermenigvuldigen met de helft van de omtrek [ΠR].

Om de inhoud van de bol [4ΠR³/3] te berekenen vertrekt Adelbold vanuit een kubus waarvan de zijden even lang zijn als de diameter van de bol [D³ = 8R³]. Om een bol te bekomen neme men hiervan 11/21. Het volume van de bol is dan gelijk aan 11/21 D³ = 88/21 R³ = 4ΠR³/3 (wat voor Π dezelfde waarde oplevert, namelijk Π = 22/7). Adelbold verkrijgt dit resultaat door van het volume van de kubus 10/21 af te trekken.

Deze vergelijking met een kubus stelt hem in staat de verhouding tussen de bollen, zoals voorgesteld door Macrobius, te verklaren. Een kubus waarvan de zijden dubbel zo lang zijn als die van een andere kubus, heeft inderdaad een inhoud die acht maal zo groot is. Aan de andere kant ontstond door het verband tussen het vierkant en de cirkel het probleem van de kwadratuur, dat door Franco van Luik zou aangesneden worden.

Brief van Gerbert aan Adelbold over variaties bij de berekening van het oppervlak van een gelijkzijdige driehoek

Deze brief is een antwoord op een verloren gegane brief van Adelbold, waarin volgend probleem naar voor werd geschoven: op basis van de door Gerbert toegestuurde figuur van een gelijkzijdige driehoek met zijden van 30 voet en een hoogte van 26 voet, bekwam hij door toepassing van de geometrische formule [basis x hoogte/2] een oppervlak van 390 kwadraatvoet, terwijl hij na gebruik van de rekenkundige formule van de driehoeksgetallen een resultaat verkreeg van 462 kwadraatvoet. Driehoeksgetallen (Boëthius, Arithmetica, II, 7) zijn getallen die kunnen voorgesteld worden door in een driehoek geplaatste punten. Ze corresponderen met een rekenkundige reeks met 1 als verschil (som van alle gehele getallen). De som van de eerste dertig gehele getallen bedraagt 462 (men kan dit ook op een andere manier berekenen: zijde² + zijde/2).

Gerbert legt uit dat de meetkundige formule de juiste is. Past men de aritmetische formule toe, dan verkrijgt men 28 kleine ruiten waarvan elke zijde gelijk is aan de meeteenheid.

[p. 30]

De briefwisseling tussen Radulf en Ragimbold

De wiskundige briefwisseling tussen Ragimbold, ‘generalissimus scolasticus’ te Keulen en Radulf, eerst ‘magister specialis’ en nadien ‘scolarum magister’ aan de kathedraalschool van Luik, werd uitgegeven door Paul Tannery en abbé Clerval, naar een handschrift (BN Lat. 6401) uit de 11de eeuw. Aangezien Fulbert (†1028) volgens dit werk nog steeds in leven is en Adelbold erin wordt vernoemd als bisschop van Utrecht, dateert de briefwisseling uit de periode 1010-27 (vermoedelijk eerder het einde van deze periode). De eerste briefschrijver staat - dankzij Adelman - bekend als een oud-leerling van de school van Chartres die aan de oevers van de Rijn aan jonge barbaren Latijn onderwees. Nadat hij te Keulen tot een Europese bekendheid was uitgegroeid, vestigde hij zich opnieuw te Luik, waar hij ook overleed. Franco van Luik vernoemt hem in zijn werk. Het lijkt er echter op dat Ragimbold te Luik studeerde. Zelf beweert hij in zijn brieven dat hij gedurende een korte tijd in Chartres heeft verbleven. Hij zegt ons dat hij gedurende twintig jaar les heeft gegeven en dat hij zijn loopbaan zou beëindigen om naar Rome te trekken. Vermits de eerste versie van de Rythmus ten laatste uit 1033 dateert, is hij vóór deze datum overleden.

Radulf is minder bekend. Hij was geen scholaster, maar slechts één van de schoolmeesters over wie Wazon de leiding had. Ook hij was een oud-leerling van Chartres. Aangezien hij noch in de eerste (1028-33), noch in de tweede versie (1048) van de Rythmus wordt vermeld, overleed hij na 1048.

Deze briefwisseling is een ware krachtmeting, waarbij de publieke bekendmaking van de brieven door geen van beide partijen werd geschuwd (‘iudicent lectores’). Radulf had nog een broer (of confrater), Odulf, die zelf ook te Chartres had gestudeerd en bij wie hij te rade ging. Radulf lichtte ook Adelbold in over de stand van zaken. Voordat hij één van zijn brieven naar Ragimbold verstuurde, vroeg hij zijn vriend Razechin, die vlakbij Luik woonde, om advies.

De commentaar van Adelbold op Boëthius

Voor de volgende generatie gold Adelbold als een autoriteit op het vlak van de mathematica; dit blijkt onder meer uit het feit dat Radulf en Ragimbold hem van hun discussie op de hoogte hielden. Spiritueel gezien was Adelbold een volgeling van Boëthius. Hij behandelde de getallen niet omwille van de getallen

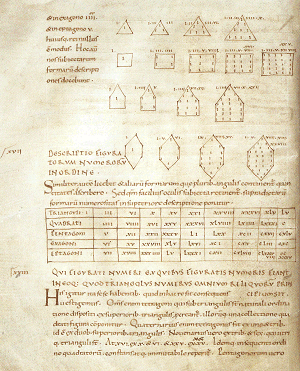
Driehoeksgetallen in de Aritmetica van Boëthius. Handschrift, 11de-12de eeuw, afkomstig van de benedictijnen van Gembloers. Brussel, Koninklijke Bibliotheek Albert I, Hs. 5444-46, f. 18 v^o. © K.B. ▪

zelf, maar omwille van hun mystieke waarde. Hij schreef immers een commentaar op één van de meest pythagoreïsche passages uit De consolatione philosophiae van Boëthius, waarin de idee naar voor wordt geschoven dat de getallen de archetypes zijn die zorgen voor de orde in het heelal, een passage waardoor later ook Kepler gefascineerd zou zijn.

Franco van Luik

Franco moeten we situeren in Luik, waar hij in 1057 werd vermeld als kanselier en van 1066 tot 1083 als scholaster. Omstreeks 1050 droeg hij aan aartsbisschop Herman II van Keulen (1036-1056) een verhandeling op met als titel De quadratura circuli. Voor de redactie van dit werk deed hij waarschijnlijk een beroep op Falchalin, scholaster van Saint-Laurent. Het vraagstuk

[p. 31]

dat in Franco's verhandeling wordt besproken en waarvan de spreekwoordelijke onmogelijkheid in de loop van de 19de eeuw werd aangetoond, bestaat erin een vierkant te construeren waarvan het oppervlak gelijk is aan dat van een gegeven cirkel. De Grieken hadden zich al afgevraagd hoe dit probleem moest worden opgelost. Ze hadden vastgesteld dat de verhouding tussen de omtrek en de diameter van de cirkel een vaste waarde is, gelijk aan de verhouding tussen het cirkeloppervlak en het oppervlak van een vierkant waarvan iedere zijde even lang is als de straal van de cirkel. Deze waarde wordt sinds Leonhard Euler (1707-1783) aangeduid met de benaming Π. Archimedes had reeds vastgesteld dat deze waarde kleiner is dan 3 1/7 en groter dan 3 10/71, met andere woorden 3,14084 < Π < 3,14285...Franco van Luik kende echter niets van Griekse meetkunde. Zoals we verder zullen zien, had hij absoluut geen notie van meetkundige bewijsvoering en verwarde hij een benaderende constructie met een theoretische oplossing. De door hem

Briefwisseling tussen Radulf en Ragimbold. Parijs, Bibliothèque Nationale. Lat 6401. © B.N. ▪

gebruikte waarde van Π = 3 1/7, die hij haalde bij Romeinse ‘agrimensores’ en bij Adelbold, stelde hij niet in vraag.

Het vertrekpunt van zijn onderzoek is Boëthius' commentaar op de Categorieën van Aristoteles. Hierin zegt de Stagiriet dat de kwadratuur van de cirkel tot het onderzoeksterrein van de wetenschap behoort indien ze uitvoerbaar is, maar dat de oplossing van dit vraagstuk voorlopig nog niet is gevonden. Boëthius voegt er nog aan toe dat de oplossing ervan pas werd gevonden ná Aristoteles. Franco vermeldt dat zowel Adelbold, Wazon als Gerbert tevergeefs pogingen hebben ondernomen.

Franco was een goed logicus, die bij ieder vraagstuk de verschillende mogelijkheden van elkaar onderscheidde. Hij was tevens een uitstekend rekenaar, die het werken met de onhandige Romeinse breuken onder de knie had. Hoewel hij als meetkundige slechts een middelmatig figuur slaat - hij ontbeerde immers iedere notie van de meetkundige bewijsvoering - is dit hoofdzakelijk te wijten aan zijn gebrekkige intellectuele uitrusting. Het lijkt erop dat hij zich ook met astronomie heeft beziggehouden, aangezien Sigebert van Gembloers in zijn De scriptoribus ecclesiasticis aan hem een tot hiertoe onvindbaar werk over computatie toeschrijft. Of Franco aandacht heeft besteed aan een andere tak van het quadrivium, de muziek, is niet zeker. Net zoals zijn voorgangers kwam hij er niet toe het elementaire theorema te bewijzen dat stelt dat de som van de hoeken van een driehoek gelijk is aan die van twee rechte hoeken.

Bronnen en problemen

Het belangrijkste probleem waarmee de meetkunde in de 9de eeuw te kampen had, was de afwezigheid van Euclides. De Elementen van Euclides werden door Boëthius in het Latijn vertaald. Dit werk ging echter erg vroeg verloren. Er werden slechts een aantal uiteenzettingen overgeleverd, echter zonder de bijhorende bewijzen. Men had ze als het ware herleid tot meetkundige ‘recepten’. Het was pas in de eerste helft van de 12de eeuw dat Euclides in Europa werd ingevoerd dankzij vertalingen van Gerard van Cremona (1114-1187), Adelard van Bath (fl. ca. 1130) en Herman van Karinthië (fl.1138-1143).

De meetkundige kennis van de Lotharingse wiskundigen stamde uit de Vroege Middeleeuwen. Een vergelijking tussen de Geometrie van Gerbert, de Geometria

[p. 32]

incerti auctoris en twee apocriefe meetkundige werken op naam van Boëthius, stelt ons in staat de Lotharingse meetkundigen in een groter geheel te plaatsen, waarvan het wetenschappelijke niveau wordt bepaald door de aard van de gebruikte bronnen. Het is algemeen bekend dat de meetkundigen uit de Vroege Middeleeuwen hun kennis aan Romeinse landmeters ontleenden. Met het oog op de aanleg van kampen, de verdeling van het land in ‘coloniae’ en de kadastratie stelden de Romeinen een gespecialiseerd corps samen, bestaande uit ‘gromatici’ of ‘agrimensores’, dat er eigen werkmethoden op nahield en zich onafhankelijk opstelde tegenover de speculatieve meetkunde. Hun technische handleidingen werden in de loop van de 4de eeuw samengebundeld in een ‘corpus’ dat voortdurend werd aangevuld. Twee wiskundige verhandelingen nemen hierin een bijzondere plaats in: de Podismus, lange tijd toegeschreven aan Marcus Junius Nipsus en het liber van Epaphroditus en Vitruvius Rufus. Men is van mening dat het mooiste handschrift met geschriften van de ‘agrimensores’, de Arcerianus A van Wolfenbüttel (6de of 7de eeuw), zich in 983 in Bobbio bevond, waar Gerbert - die abt van dit klooster was geworden - het misschien heeft kunnen consulteren.

Nu we het algemeen kader hebben omschreven, kunnen we voortgaan met een analyse van de probleemstellingen van de Maaslandse meetkundigen.

➊

De problemen in verband met de cirkel en de bol worden behandeld in de brief van Adelbold aan Gerbert en in De quadratura circuli van Franco. Adelbold vertrekt vanuit een beschouwing van Macrobius in diens In somnium Scipionis, terwijl Franco vertrekt vanuit een passage uit de commentaar op de Categorieën van Boëthius. Dit wijst zowel op een gebrek aan wetenschappelijke handleidingen als op een onderwerping van het quadrivium aan de filosofische exegese. Om het oppervlak van een cirkel en het volume van een bol te berekenen geeft Adelbold aan Π de waarde van 22/7. Deze methoden en deze waarde van Π werden algemeen aanvaard, aangezien ze zowel in de Geometria incerti auctoris als in de Geometria II van Boëthius konden teruggevonden worden. Meer dan waarschijnlijk is de bron van beide auteurs van gromatische aard, vermits Franco aan Epaphroditus zelfs de numerieke waarde van de diameter heeft ontleend. De vermelde waarde van Π werd in 1048 eveneens gebruikt door Herman de Lamme in zijn briefwisseling met Meinzo van Konstanz, met betrekking tot de bepaling van de omtrek van de aarde door Eratosthenes. Ook hij maakte hierbij gebruik van Macrobius.

➋

De geometrie van de driehoeken wordt behandeld in de brief van Gerbert aan Adelbold en in verschillende passages van de briefwisseling tussen Radulf en Ragimbold. a) Gerbert en Adelbold maken geen duidelijk onderscheid tussen de aritmetische formule van de driehoeksgetallen en de meetkundige formule voor de berekening van het oppervlak van een driehoek. Hoe ongewoon deze verwarring ook mag lijken, het is wel zo dat de formules voor de polygonale getallen die betrekking hebben op de oppervlakken terug te vinden zijn in de Geometria incerti auctoris en in Geometria II en zelfs tot in de 12de eeuw konden aangetroffen worden in de ‘praktische’ meetkunde, de zogenaamde Artis cuiuslibet consummatio. Het is niet Boëthius die aan de basis hiervan ligt maar wel de Romeinse landmeters, vermits Epaphroditus de polygonale getallen voorstelt als het oppervlak van een veelhoek, wat zeker de grondeigenaars voor bepaalde moeilijkheden moet gesteld hebben. b) Naar aanleiding hiervan kwam Gerbert terug op de berekening van de hoogte van een gelijkzijdige driehoek in verhouding tot de zijde. In het eerder verstuurde werk bedraagt de verhouding tussen de loodlijn en de zijde 26/30, wat voor √3 (1,73205) de waarde 26/15 (= 1,73) oplevert. Deze waarde berust niet zoals men zou verwachten op de kennis van het theorema van Pythagoras. Ze werd direct ontleend aan de ‘agrimensores’ en ze is terug te vinden in de Geometria incerti auctoris, alsook in Geometria II. In de door ons bestudeerde brief is Gerbert echter reeds verder geëvolueerd. Hij stelt de loodlijn gelijk aan 6/7 van de zijde, wat voor √3 de waarde 12/7 of 1,71 oplevert, een waarde die veel minder precies is en waarvan we de oorsprong niet kunnen achterhalen. Gerbert voegt er aan toe dat de hoogte gelijk is aan 6/7 van de zijde. Waarschijnlijk door toepassing van de stelling van Pythagoras: h^2 = z2 - z^2/4 → h = √3/4 z^2 bekomt hij de benaderde waarde van √3 = 12/7. Men bekomt dus dat h = 6/7 z (de hoogte = 6/7 van de zijde). c) Radulf en Ragimbold houden zich in hun brieven met gelijkaardige vraagstukken bezig. Ze behandelen bijvoorbeeld het probleem van de constructie van een vierkant dat dubbel zo groot is als een gegeven vier-

[p. 33]

kant op de wijze als is besproken door Boëthius in zijn commentaar op de Categorieën. Ragimbold weet net zo goed als Franco en de auteur van de Geometria incerti auctoris dat de diagonaal van een vierkant in lengte overeenkomt met de zijde van een vierkant dat dubbel zo groot is. In hun pogingen de verhouding van deze diagonaal ten opzichte van de zijde te bepalen, met andere woorden √2 (1,41421), bekomt Radulf 7/5 (1,4) en Ragimbold 17/12 (1,4166). Laatstgenoemde heeft zich hiervoor gebaseerd op Boëthius' Geometria I, waarvan ten minste één exemplaar in een Luikse bibliotheek aanwezig was. Hierbij merken we op dat de Geometria incerti auctoris voor deze verhouding een waarde opgeeft van 4/3 (1,3333). d) De commentaar op de Categorieën beschouwt het als een algemeen bekend gegeven dat de som van de binnenhoeken van om het even welke driehoek gelijk is aan twee rechten (Euclides, 1, 32). Het vraagstuk wordt door Ragimbold aangehaald in een verloren gegane brief. Radulf probeert het op te lossen door middel van een methode die hij aan dezelfde tekst van Boëthius heeft ontleend; hij slaagt echter niet in zijn opzet, tenzij voor een gelijkbenige rechthoekige driehoek. Voor de overige driehoeken erkent hij dat de oplossing gemakkelijker verstandelijk te bevatten is dan dat ze op schrift kan worden gesteld. Hij schuift het probleem dan ook terug naar zijn gesprekspartner, die spreekt over experimentele verificatie (‘numeris et mensuris probando’). In werkelijkheid kan de stelling dat de drie binnenhoeken van een driehoek gelijk zijn aan twee rechten zonder enige vorm van bewijs teruggevonden worden in de Geometrie van Gerbert, die naar dezelfde commentaar van Boëthius op de Categorieën verwijst.

➌

Dit probleem kón trouwens niet opgelost worden, want het wierp een terminologisch vraagstuk op dat door Ragimbold werd geformuleerd, namelijk: wat zijn juist de binnen- en buitenhoeken van een driehoek? Voor ons worden de buitenhoeken gevormd door een zijde en het verlengstuk van een andere zijde. Radulf antwoordt dat de binnenhoek op een plat vlak in een driedimensionale ruimte wordt beschouwd als de buitenhoek, zoals de gestrekte hoek van een kubus. Ragimbold is een andere mening toegedaan en wordt hierin gesteund door Fulbert. Volgens hem vormt de buitenhoek een stompe hoek die groter is dan een rechte hoek, terwijl een binnenhoek een scherpe hoek is, aangezien hij kleiner is dan een rechte hoek. Vervolgens probeert hij de twee vermeldingen van buitenhoeken in Geometria I met deze definitie in overeenstemming te brengen. Het onderwerp van discussie zelf lijkt ons absurd. Dit is het echter niet wanneer men weet dat de ‘agrimensores’, bij vergelijking met een rechte hoek, de scherpe hoeken binnenhoeken noemden en de stompe hoeken buitenhoeken. Dit is ook het geval in de Geometrie van Gerbert. Een ander terminologisch vraagstuk situeert zich in dezelfde context: Radulf vraagt aan Ragimbold wat ‘pedes recti, quadrati, crassi’ (rechte, vierkante en kubieke voeten) zijn. Hij herinnert zich dit te hebben gelezen in het boek van Albinus te Chartres. Zoals we later zullen vaststellen werd deze vraag misschien ingegeven door een passage uit de brief van Gerbert aan Adelbold. Ragimbold geeft een antwoord van eigen vinding, want over dit onderwerp heeft hij geen literatuur. Eveneens bij gebrek aan informatie uit Radulf de wens over de Podismus te kunnen beschikken, maar de twee werken waren noch in Keulen, noch in Luik beschikbaar. De verwijzing naar de gromatische traditie is expliciet aanwezig, want de ‘agrimensores’ gebruikten ‘pedes quadrati’ voor ‘pedes solidi’, i.e. kubieke voeten. Dit was nog steeds het geval toen Gerbert zijn Geometrie schreef, terwijl zijn terminologie sterker was geworden wanneer hij zijn brief aan Adelbold schreef. De Podismus waaruit ze meenden hun kennis te kunnen putten, is een verhandeling van de pseudo-Nipsus. Wat de auteur van de Albinus betreft, moeten we zonder twijfel denken in de richting van Alcuinus, hoewel een preciese lokalisatie niet mogelijk is.

Uit dit alles mag blijken dat de wiskundigen bij hun werk, net zoals de andere meetkundigen uit de Vroege Middeleeuwen vóór de verspreiding van de Grieks-Arabische wetenschap, aangewezen waren op zuiver literaire bronnen, die hen enerzijds confronteerden met het probleem van de speculatieve geometrie en anderzijds met dat van de technische traditie, die hen een ontoereikende uitrusting bood om de problemen op te lossen.

▫ Aritmetica

Lotharingen had al lang een bloeiende aritmetische traditie. Van de hand van Notger bezitten we slechts een scholie bij Boëthius' aritmetica over een aritmetische verhouding. Wazon, zijn opvolger als bisschop, begon zijn loopbaan in deze school. Hij zorgde voor het abacus en voor de boeken van de leerlingen.

[p. 34]

In de 11de eeuw schreef de abacist Bernelius over de kunst van het rekenbord Lotharienses...quod in his cum expertus sum florere. De oude bibliotheekscatalogi vermelden talrijke aritmetische werken, verhandelingen over het werken met een abacus en traktaten over breuken (‘minutiae’).

Analyse van de belangrijkste werken

Om het wetenschappelijke niveau te bepalen van de Lotharingse rekenkundigen beschikt men over verschillende bronnen: de verhandeling van Heriger, het deel over aritmetica in Geometria II en de verhandeling over het telraam van Herman de Lamme (Regulae Herimanni qualiter multiplicationes fiant in abaco). Bovendien bestaan er nog een aantal onuitgegeven verhandelingen.

Wanneer Heriger juist werd geboren, is niet bekend (alvast vóór 950). Op jonge leeftijd trad hij in bij de monniken van de abdij van Lobbes, waar hij eerst studeerde en nadien zelf les gaf. Hij stond er onder meer in voor de vorming van Burchard, de latere bisschop van Worms, van Olbert, de latere abt van Gembloers, en van Adelbold. Hij werd raadsheer en vertrouweling van Notger (vóór 980) en vergezelde hem in Italië. Op 21 december 990 werd hij verkozen tot abt van Lobbes. Hij bestuurde de abdij tot aan zijn dood op 31 oktober 1007, zes maanden voor het overlijden van Notger (10 april 1008).

Het werk van Heriger handelt in hoofdzaak over theologie, hagiografie en geschiedenis. Zijn wetenschappelijke nieuwsgierigheid wordt echter duidelijk in de mooie kosmologische proloog van de Gesta episcoporum Tungrensium Trajectensium et Leodiensium, waarin hij, in de geest van Augustinus, uiteenzet dat God de wereld heeft geschapen met een vast gewicht en een vaste omvang en verhouding, er rekening mee houdend dat de vier elementen met elkaar in evenwicht zijn en dat alles past binnen het kader van de vier windrichtingen, waarin hij trouwens het symbool van het kruis herkent.

De kroniekschrijver Alberic de Trois-Fontaines (begin 13de eeuw) schrijft hem een werk toe met als titel Regulae numerorum super abacum Gerberti, de Regel der getallen op het abacus van Gerbert. Alleen al deze titel volstaat om de nauwe verwantschap aan te tonen tussen het wiskundig onderzoek van Heriger en dat van zijn Reimse meester. Men weet immers dat het gebruik van Romeinse cijfers zelfs voor de meest eenvoudige vermenigvuldigingen en delingen een quasi onoverkomelijk obstakel was, vooral omwille van de additieve (XI, VI), subtractieve (IV, IX) en multiplicatieve (L, D) symbolen, die verschillen al naargelang het om eenheden, tientallen of honderdtallen gaat. Gerbert bracht aan het rekenbord verbeteringen aan. Het abacus bestond uit een bord met 27 kolommen, welke overeenkwamen met onze eenheden, tientallen, honderdtallen, duizendtallen, tienduizendtallen, honderdduizendtallen, enz. Op dit bord verschoof men ‘apices’, hoornen rekenpenningen waarop de cijfers 1 tot en met 9 waren aangebracht en die zo, al naargelang de kolom waarin ze werden geplaatst, een bepaalde waarde aannamen. De lege vakjes waren gelijk aan nul. Gerbert formuleerde een geheel van regels voor de berekeningen waarmee, volgens de getuigenis van William of Malmesbury (1090/96-ca. 1143), de abacisten heel wat moeite hadden.

Als voorbeeld tonen we de vermenigvuldiging van 4.600 met 23:

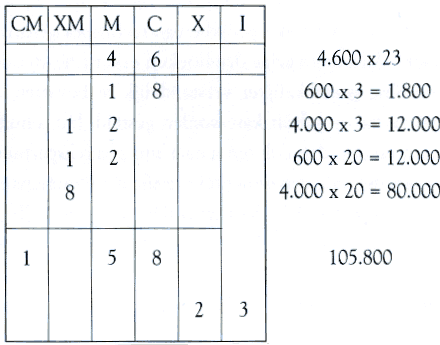
Voorbeeld van een vermenigvuldiging met een abacus. © C.H.S.T. ▪

Gerbert schreef de Regulae de numerorum abaci rationibus. Een ander werk van hetzelfde type, door Olleris aan Gerbert toegeschreven, werd door Bubnov uitgegeven onder de naam van Heriger. Het tweede deel van deze verhandeling (Aliae regulae Herigeri in abacum) wordt door de handschriften op naam van Heriger gesteld. Bij ten minste twee gelegenheden werden aan die werk veranderingen aangebracht, wat het belang ervan aantoont.

In tegenstelling tot wat Albéric de Trois-Fontaines beweert, is het werk van Heriger geen commentaar op dat van Gerbert. Voor het uitvoeren van een deling

[p. 35]

Astrolabium. Luik, Musée de la Vie Wallonne. © M.V.W. ▪

rijkt hij een originele methode aan die erg veel lijkt op de huidige. Het lijkt er eerder op dat hij dezelfde bronnen gebruikte als Gerbert. Aldus zorgde Heriger voor de invoering van het rekenen met een abacus in het Maasland. In de daaropvolgende eeuw zouden Helbert van Luik, monnik te Saint-Hubert en Wazon, prinsbisschop van Luik, dit instrument in de Luikse scholen uitproberen.

De Arabische invloed

Het probleem hier is eenvoudig: wat stond er juist op de ‘apices’? Volgens Richer ‘verbond Gerbert aan de 9 cijfers duizenden hoornen karakters die, wanneer ze op de 27 kolommen van het telraam werden verschoven, het mogelijk maakten om de vermenigvuldiging of deling van om het even welk getal uit te voeren’.

De ‘apices’ konden ofwel Romeinse cijfers, ofwel overeengekomen tekens (initialen), ofwel ‘Arabische cijfers’ dragen. Deze laatste benaming is vervangen door de omschrijving ‘Toledaanse cijfers’, aangezien ze sinds de 10de eeuw in Spanje ingeburgerd waren en onder invloed van de Visigotische schrijfwijze van de Romeinse cijfers een wijziging hadden ondergaan.

Deze ‘Toledaanse cijfers’ zijn in twee golven tot Europa doorgedrongen: vooreerst via de ‘apices’, waarvan de ronde vorm verklaart waarom de cijfers soms fouten bevatten - af en toe staan ze op hun kop - vervolgens via de Algorismus, de aritmetica van al Khwarizmi die waarschijnlijk in de 12de eeuw te Toledo in het Latijn werd vertaald.

In de oudste handschriften van Gerbert dragen de ‘apices’ Romeinse cijfers. Hetzelfde geldt voor die van Herman de Lamme in zijn verhandeling over de vermenigvuldiging en deling van getallen door middel van het abacus. Een heden te Parijs bewaard handschrift (BN 8663) bewijst dat het abacus van Heriger gemengd was: de cijfers waren Romeins, maar iedere groep van drie kolommen (boog van Pythagoras) werd met een ‘Arabisch cijfer’ genummerd. In de tweede geometrie van Boëthius verschijnen de ‘Toledaanse cijfers’ tweemaal: een eerste keer in de loop van de tekst om cijfers voor te stellen die men nodig heeft voor de berekeningen, een tweede keer op het abacus om de kolommen te nummeren.

▫ Astronomie

Getuigenissen over de beoefening van de astronomie in Lotharingen zijn weinig talrijk en evenmin veelzeggend. De astronomie werd gecultiveerd onder de elementaire vorm van computatie. Hiermee was men in staat de datum te bereken waarop wisselende feestdagen vielen, in het bijzonder Pasen. Immers, de datum van Pasen wordt volgens de Hebreeuwse kalender bepaald door de fasen van de maan. De Juliaanse (christelijke) kalender daarentegen is een zonnekalender. Bijgevolg varieert de Paasdatum en moet men zonnejaren en maanjaren met elkaar combineren in cycli, onder dewelke die van negentien jaar de meest praktische is (men was van mening dat negentien zonnejaren ongeveer overeenkwamen met 235 maanmaanden). Dit probleem lag aan de basis van talrijke werken. De bekendste zijn de Computus Paschalis van Cassiodorus, de Computus van Isidorus en de werken van Beda Venerabilis, Rabanus Maurus, Hilperic en

[p. 36]

Heric van Auxerre. De Luikse monnik Engelbert, verbonden aan de abdij van Saint-Laurent, verzamelde heel wat astronomische kennis met betrekking tot computatie en schreef over dit onderwerp een aantal voorschriften. Franco hield er zich eveneens mee bezig en in de daaropvolgende eeuw stelden Renier van Saint-Laurent en Sigebert van Gembloers een computatie samen naar het voorbeeld van Beda Venerabilis.

Andere verwijzingen zijn sprekender. Franco van Luik zou de auteur zijn van een verhandeling over de sfeer. Men moet hier ongetwijfeld de driedimensionale sfeer onder verstaan, een astronomisch instrument voor de stereografische projectie van de hemel dat op dezelfde manier werd gebruikt als een astrolabium. Gerbert had hieromtrent de theorie overgemaakt aan zijn vriend Constantinus van Fleury. Hij zond ook een ‘sphaera’ naar een monnik in Trier.

Het gaat over hetzelfde onderzoeksthema wanneer Radulf aan Ragimbold schrijft: ‘Ik zou u een astrolabium toegestuurd hebben, maar wij hebben het onze nodig om er een kopie van te vervaardigen. Indien u zich hierover wenst te informeren, kom dan naar de mis in Saint-Lambert, want het volstaat niet een astrolabium enkel maar te bekijken’. Deze tekst bevat één van de vroegste vermeldingen van het astrolabium in het Westen. Het astrolabium werd vooral gebruikt om de hoeken te meten tussen twee gegeven voorwerpen, wat men name belangrijk was bij de bepaling van de hoogte van hemellichamen. Het is een uitvinding van de Grieken die door de Arabieren aanzienlijk werd verbeterd. In Toledo had men zich gespecialiseerd in de vervaardiging ervan. Het astrolabium drong via het Catalaanse klooster van Ripoll en dankzij Gerbert in het Westen door. We vinden het terug in Chartres onder Fulbert en vóór 1084 bezat men in Toul een handschrift met als titel Girberto de astrolapsu.

Het Luiks astrolabium lijkt van Arabische oorsprong. Waarom kon men het zien tijdens de mis in Saint-Lambert? Het is mogelijk dat het gebruikt werd om het uur te bepalen. Dit probleem is volledig doorgelicht door Arno Borst, die het in verband heeft gebracht met de kerkelijke hervormingen.

De duidelijkste bevestiging van een Arabische afkomst is terug te vinden in de geschriften van de tijdgenoot Herman de Lamme, wiens banden met de Lotharingse wiskundigen we reeds hebben onderstreept. Herman de Lamme werd geboren in Altshausen op 18 juli 1013. In 1043 werd hij monnik te Reichenau, maar hij overleed in zijn geboorteplaats op 24 september 1054. Hij is de auteur van twee werken over het astrolabium. Het eerste, De utilitatibus astrolabii, wordt al van in de 12de eeuw aan hem toegeschreven. Het omvat 21 hoofdstukken die elk afzonderlijk ook teruggevonden kunnen worden onder de naam van Gerbert en een commentaar op de bepaling van de omvang van de aarde door Eratosthenes volgens Macrobius die reeds in 1048 besproken werd in de briefwisseling met Meinzo. Het tweede werk, Mensura astrolabii, is een beschrijving van een Arabisch astrolabium. Het bevat een groot aantal gelatiniseerde Arabische termen. Herman kende ook twee andere Arabische instrumenten, de ‘chilinder’ en het kwadrant met schuiflatje.

Het zou evenwel onjuist zijn de betekenis van de Arabieren voor de Lotharingse wiskundeschool te overwaarderen. De problematiek heeft geen fundamentele wijzigingen ondergaan. Al wat verspreid werd, zijn werktuigen: een abacus met een zakje ‘apices’ en een astrolabium. Dat is ook de reden waarom deze eerste verhandelingen dikwijls de vorm aannamen van ‘gebruiksaanwijzingen’.

▪ De 12de eeuw

De Arabische wetenschap drong vanaf het begin van de 12de eeuw door via twee, ver van Lotharingen verwijderde gebieden. Het grootste deel van de Arabische kennis werd via Spanje - en dan vooral via Toledo - verspreid. Op Sicilië maakte men zowel vertalingen uit het Grieks als uit het Arabisch. Op het einde van de 12de eeuw zou Constantinopel op dit vlak een steeds belangrijker rol gaan vervullen.

De wegen der kennis leidden achtereenvolgens naar Salerno, Montpellier, Chartres en Parijs, om tenslotte ook Lotharingen te bereiken. De school van Salerno bestond reeds in de 11de eeuw dankzij de verworvenheden van de monastieke geneeskunde. Constantinus Africanus, monnik te Monte Cassino maar van maghrebijnse afkomst, zorgde voor een eerste versmelting, die in de 12de eeuw tijdens het Hoog Salerno verder zou geëxploiteerd worden. Een mooi voorbeeld hiervan is het corpus van referentiewerken bekend onder de naam Codex van Breslau. Wibald van Stavelot (1097-1158) bracht in 1137 een bezoek aan Salerno terwijl Petrus Venerabilis (ca. 1094-1156) vanuit Cluny over geneeskundige onderwerpen correspondeerde met Bartholomaeus van Salerno.

[p. 37]

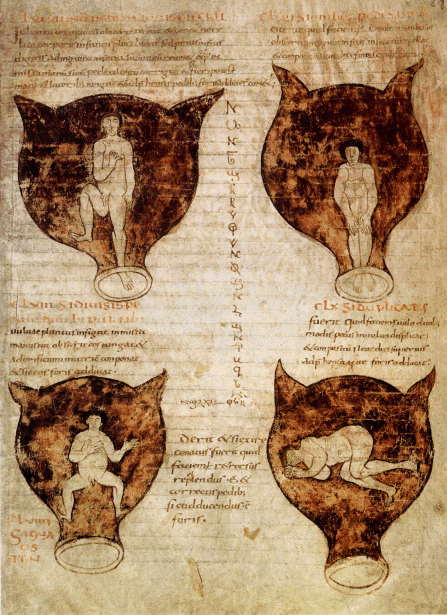
Mustio, Gynaecia. Houding van het kind in de baarmoeder. Brussel, Koninklijke Bibliotheek Albert I, Hs. 3701-15 f. 28 r^o. © K.B. ▪

[p. 38]

Eveneens in 1137 bracht Adalbert II (†1141), aartsbisschop van Mainz, een bezoek aan Montpellier, nadat hij eerst zijn kennis had verrijkt in Hildesheim, Reims en Parijs. Volgens hem was Montpellier een stad ‘waar de “ph0ysica” (geneeskunde) haar woning en tempel had, waar de geneesheren de leerstellingen en voorschriften van de geneeskunde onderwezen, de zieken genazen en de gezonden voor ziekte behoedden’. Dit relaas, gerapporteerd door Anselmus van Havelberg (†1158), vormt de oudste getuigenis over Montpellier. De oorsprong van de school voor geneeskunde is slechts vaag gekend en de rol die de joden en de Arabieren hierin hebben gespeeld, moet nog worden bepaald. Wat volgens Johannes van Salisbury (†1180) wel vaststaat, is dat men vanuit Salerno en Montpellier terugkeerde ‘met een lading barbaarse woorden’. Vreemd genoeg is het Havelberg die ons heeft voorzien van een zeer belangrijk handschrift over de Arabische astrologen, dat nu wordt bewaard te Berlijn.

De scholen van Chartres, die vele banden hadden met Lotharingen, vormden eveneens een verplichte rustplaats. Adelard van Bath stopte er op zijn reis naar Salerno. Thierry de Chartres (†1155) kende de door Domingo Gundisalvo (fl. 12de eeuw) vertaalde De coelo et mundo van Aristoteles en Herman van Karinthië droeg aan hem zijn De essentiis op, alsook zijn vertaling van de wereldkaart van Ptolemaeus. Guillaume de Conches (†1154) kende Constantinus Africanus en was vertrouwd met de Isagoge van Johannitius (Hunayn ibn Ishaq, 808-873), terwijl Bernardus Silvestris (†1153) in zijn Experimentarius een uit het Arabisch vertaalde geomantiek op rijm zette. In de tweede helft van de 12de eeuw zou de rol van de scholen van Chartres geleidelijk worden overgenomen door de Parijse scholen.

Na 1100 was de zin voor onderzoek in Lotharingen niet langer dezelfde. Het is bekend dat de Lotharingse scholen in verval geraakten of zich eerder naar andere onderwerpen richtten. Er was niet langer sprake van een geheel van leerstellingen ondersteund door een corps van geleerden. De ontwikkeling van de nieuwe kennis behoorde tot het terrein van de individuen en handschriften. Uit de opeenstapeling van al hun omzwervingen kan men afleiden volgens welke richtingen de verschillende invloeden zich hebben laten gelden. In afwachting van een volledig overzicht zal men zich met een aantal voorbeelden moeten tevreden stellen.

▫ Handschriften en bibliotheekscatalogi

De niet altijd even duidelijke vermeldingen over de herkomst van de handschriften moeten in verband worden gebracht met de gegevens uit de oude bibliotheekscatalogi.

De handschriften over geneeskunde zijn verhelderend. De uit het Arabisch vertaalde geneeskundige werken veroorzaakten niet dezelfde breuk als de algoritmische werken, de euclidische stellingen of de filosofie van Aristoteles. Het Grieks-Arabisch galenisme nam de plaats in van het - in hoofdzaak benedictijns - galenisme uit de Vroege Middeleeuwen. Het werk van Constantinus Africanus is een zuiver product van deze versmelting.

In de Lotharingse handschriften en bibliotheekscatalogi nam de nieuwe geneeskunde geruisloos haar plaats in naast de oude. Zo vermengt het handschrift KB 2419-31, bewaard in de Koninklijke Bibliotheek te Brussel en afkomstig uit de Luikse abdij van Val Saint-Lambert, de erfenis van de Romeinse geneeskunde uit de keizertijd met de vertalingen van Constantinus Africanus en de originele verwezenlijkingen uit de omgeving van Salerno. Tot de oude traditie behoren het Liber medicinalis van Quintus Serenus Sammonicus (2de eeuw), een bundel met geneeskundige voorschriften in versvorm, de Medicina ex oleribus et pomis (geneesmiddelen bereid met groenten en met fruit) van de veearts en agronoom Gargilius Martialis (†ca. 260) en de Brief aan Pentadius van de Afrikaanse geneesheer Avianus Vindicianus (2de helft 4de eeuw), die handelt over de gemoedsgesteldheid. Tot de Arabisch-Latijnse stroming behoren de twee bekendste vertalingen van Constantinus Africanus, Dietae universales et particulares, (algemene en bijzondere regimes) van Ishaq ibn Sulaiman al-Israeli (Isaac Judaeus, eerste helft 10de eeuw) - een synthese van de Griekse en Arabische theorieën over de levensmiddelen - en een fragment uit de Pantechne (‘de algemene geneeskunde’), een vertaling van de uitgebreide encyclopedie Kitab al Malaki (‘het koninklijk boek’) van Ali ibn al-abbas al Magusi (Hali Abbas, tweede helft van de 10de eeuw). Constantinus Africanus zelf is vertegenwoordigd met zijn De gradibus. Hierin poogt hij de geneeskrachtige werking van kruiden in cijfers te vertalen volgens de vier niveaus van warmte, koude, droogte en vochtigheid, overeenkomstig de vier elementen. Het handschrift omvat tevens het Passionarius

[p. 39]

Mysterie van Apollo. Luik, Musée Curtius. © M.C. ▪

(verhandeling over de kwalen en hun genezing) van Gariopontus, één van de eerste Salernitaanse meesters, die nog niet erg beïnvloed was door de Arabieren en nog steeds schatplichtig was aan de Romeinse geneeskundigen, in het bijzonder aan Theodorus Priscianus. Door de juxtapositie van beide tradities, is de verzameling kenmerkend voor een overgangsperiode.

De catalogus van Elnone (Saint-Amand), opgesteld in de 12de eeuw, is bijzonder rijk wat geneeskundige handschriften betreft. De lijst vermeldt antieke werken (het Liber oxipati van Caelius Aurelianus, het kruidboek van Dioscorides), vertalingen uit het Grieks die in de 6de eeuw te Ravenna tot stand zijn gekomen (de Aforismen van Hippocrates, De simplicibus ad Paternianum van een pseudo-Galenus, een chirurgie, de gynaecologie van Cleopatra en Mustio), teksten uit het Vroeg Salerno (Gariopontus), vertalingen van Constantinus Africanus (De gradibus, het Liber aureus, de diëtetiek van Isaac Judaeus, de verhandeling over de urinewegen, de verhandeling over de koortsen, het Viaticum) en andere teksten die tot stand zijn gekomen in Salerno (het Antidotarium).

▫ De individuen

De grote meesters uit de 12de eeuw hadden een zeer verschillende kijk op de nieuwe wetenschap. Dom Rupert (ca. 1070-ca. 1130), magister van Saint-Laurent te Luik en nadien abt te Deutz nabij Keulen, blonk niet uit door een uitgebreide kennis van het traditionele quadrivium. Zijn theologische opvattingen daarentegen valoriseerden de menselijke arbeid ‘labor’ en vormden een ideologische afspiegeling van wat Jean Gimpel heeft omschreven als ‘de industriële revolutie van de Middeleeuwen’. Zijn invloed is merkbaar in het grote 12de-eeuwse handboek voor technologische vorming, de Diversarum artium schedula van Theophilus presbyter, dat in werkelijkheid het werk is van de monnik en edelsmid Roger van Helmarshausen. Laatstgenoemde kreeg waarschijnlijk zijn opleiding in de abdij van Stavelot. In de theologische inleidingen van de drie bewaarde Theophilus-exemplaren wordt uiteengezet hoe bij de arbeid van de mens - en dan vooral de arbeid van de edelsmid, de kunstschilder en de glazenier - de zeven gaven van de Heilige Geest worden aangewend. Het Mysterie van Apollo, een kunstwerk dat te Luik wordt bewaard en waarvoor de kunstenaar zich door Rupert liet inspireren, toont ons een sculpturale voorstelling van de belangrijke keuze tussen ‘labor’, die honing aanreikt en ‘vana cura’, de ijdele zorg, die bittere absint aanbiedt.

[p. 40]

Rupert correspondeerde tenslotte met de illustere Hildegard van Bingen (1098-1179). De geschriften van deze zalige over de natuurwetenschappen hebben haast geen invloed van de nieuwe wetenschap ondervonden, aangezien hierin het monastiek galenisme en de Rijnlandse tradities met elkaar worden vermengd.

Een heel andere persoonlijkheid was Wibald (1098-1158), abt van Stavelot. Zijn loopbaan was vooral afgestemd op het zuiden. Nadat hij abt was geweest van de abdij van Stavelot, werd hij in 1137, vijftig jaar na de dood van Constantinus Africanus en in de bloeiperiode van Salerno, abt van Monte Cassino. Op 20 oktober 1146 werd hij abt van Corvey en in deze functie leidde hij twee zendingen naar Byzantium (in 1155 en 1156). Hij had een ruime wetenschappelijke interesse. In een brief van november 1147 vermeldt hij twee geneesmiddelen, namelijk ‘diacalamentum’ (op basis van kattenkruid) en ‘diamargaritum’ (op basis van parels), die eveneens duidelijk aangehaald worden in de Salernitaanse farmacopee. Wibalds belangstelling voor geneeskunde, in het bijzonder voor diëtetiek, komt ook in andere passages uit zijn briefwisseling aan de oppervlakte. Dit verklaart de aanwezigheid in Wibalds sacramentsboek van een tekst die door Hubert Silvestre is geïdentificeerd als een vertaling van het Geheim der geheimen van een pseudo-Aristoteles.

Het Geheim der geheimen is een Arabisch werk (Sirr al-Asrãr), zogenaamd vertaald uit een Grieks origineel dat door Aristoteles aan Alexander de Grote zou zijn opgedragen en dat ontdekt werd in een tempel. In realiteit is de oorsprong van dit werk een Arabische verhandeling over de levenswijze van vorsten, handelend over politiek, moraal en gezondheid. Een verkorte Arabische versie (versie A) uit de 10de eeuw stond model voor de door ons geraadpleegde tekst, die tussen 1125 en 1142 door Johannes van Sevilla te Toledo werd vertaald. Deze vertaler was waarschijnlijk een mozarabisch geestelijke die in opdracht werkte van Raymundus van Toledo. Deze verhandeling, met als titel Epistola Anstotelis Alexandro de dieta servanda, is een praktisch werk waarin, van het ontwaken tot het slapengaan en op het ritme der seizoenen, een doordeweekse dag van een vorst wordt beschreven. Het handschrift uit Stavelot is één van de oudste van de in totaal meer dan 150 gekende exemplaren. Dit aantal duidt op een snelle verspreiding van het werk.

Tenslotte is het misschien via Stavelot dat het oudste alchimistisch recept dat in het Westen gekend is tot ons is gekomen. Theophilus, alias Roger geeft immers een vreemd recept voor de bereiding van ‘Spaans goud’ op basis van het ei van de ‘basilicus’ en bloed van een roodharige man. We vinden hiervan ook sporen bij Arabische auteurs en te Salerno.

▪ Besluit

Ondanks het onvolledig beeld is het contrast duidelijk. De Lotharingse cultuur die, meer bepaald in onze streken, uiterst ontvankelijk stond tegenover de vernieuwingen toen deze Europa binnendrongen, heeft de Arabisch-Latijnse wetenschap niet echt volledig benut. Een vergelijking met Frankrijk onder het bestuur van koning Filips-Augustus (1165-1223) dringt zich op. Guy Beaujouan spreekt van ‘de langzame opgang der wetenschappen’. Maar terwijl in Frankrijk de wetenschappen na 1200 tot volle ontplooiing kwamen, stagneerden ze in Lotharingen.

In werkelijkheid heeft de Arabisch-Latijnse wetenschap haar vruchten slechts kunnen afwerpen door de weerklank die ze in het onderwijs en in het bijzonder aan de universiteiten heeft gekregen.

In Lotharingen hebben zowel mensen als boeken talrijke paden gevolgd, maar zelden liepen ze samen en nooit mondden ze uit in de oprichting van een school. Christine Renardy heeft op zeer heldere wijze de itineraria beschreven van deze universitaire leermeesters, die voor hun vorming naar Parijs, Bologna, Salerno of Montpellier trokken, maar die naar hun land weerkeerden zonder er een trefpunt voor wetenschappelijk onderzoek op te richten.

Aan de basis hiervan lag ongetwijfeld een zekere ‘inertie van het epistemologisch veld’, om een uitdrukking van Jean Ladrière aan te halen. De Grieks-Arabische geneeskunde integreerde zich zonder moeilijkheden en de overdracht van de nieuwe inhouden gebeurde onopgemerkt. De scholen, al te sterk verbonden met het quadrivium, ontbrak het aan menselijke middelen om zich om te vormen. Ze konden slechts een propaedeuse aanbieden en hun beste krachten er op uit sturen.