Appels en peren / wiskunde en psychologie
(1984)–Hans Freudenthal–Gebundelde opstellen
[pagina 68]
| |||||||||||||||||||||||||||||||
Waarvoor verhoudingen?Ik vergelijk met elkaar de lengtes van
| |||||||||||||||||||||||||||||||
[pagina 69]
| |||||||||||||||||||||||||||||||
of tijden van
of de hoeveelheden van
of de gewichten van
of de krachten van
en het blijkt dat de één staat tot de ander als 3 staat tot 4. Waarom zo ingewikkeld? In de vierde à vijfde klas basisschool leer je breuken en in de breukentaal is dit simpelweg de één is ¾ van de ander. Breuken zijn getallen. Je kunt er lekker mee rekenen, je hoeft er zelfs niets meer van te begrijpen als je maar goed de regels kent. Waarom dan verhoudingen? Als een manier om iets ingewikkeld te zeggen, dat ook eenvoudig kan - met twee getallen: 3 staat tot 4 of 3 : 4, wat ook met één getal kan, met de breuk ¾? En waarvoor OA : OB = OA′ : OB′, als het met bij die stand van de zon is doorgaans de schaduw 3/4 van het voorwerp eenvoudiger gaat? 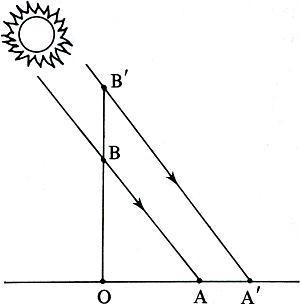
figuur 6.2
Die vragen zijn telkens weer gesteld en met wat zich in ‘New Math’Ga naar voetnoot1 heeft afgespeeld, is de knoop dan doorgehakt: verhoudingen en evenredigheden werden afgeschaft. Afgeschaft - dat wil zeggen dat het werken met en het spreken over verhoudingen door het rekenen met breuken is vervangen.
De wiskundige is op unificeren uit. Terecht, want waarvoor twee wiskundige werktuigen als je het met één kunt doen? En onterecht, want in het dagelijks | |||||||||||||||||||||||||||||||
[pagina 70]
| |||||||||||||||||||||||||||||||
leven, in de toepassingen heb je juist behoefte aan een veeltal werktuigen (én aan de wetenschap hoe het één met het ander is gerelateerd). Onterecht ook qua didactiek. Want didactiek moet rekening houden met wat aan mentale ervaringen in vaardigheden bij de leerlingen aanwezig is en met de manier waarop ze zich ontwikkelen. Juist ‘verhouding’ is een prachtvoorbeeld om zich te realiseren hoe wij - van de wieg af aan - theoretische ervaringen opdoen en vaardigheden ontwikkelen, aanvankelijk onbewust en geleidelijk bewuster. Dáár moet de didactiek bij aanknopen, bij wat in de kinderen leeft op het punt van ‘verhouding’ en er de bewustmaking van bevorderen. We opereren met verhoudingen aleer we weet hebben van getallen - zelfs bij dieren moet het verwerken van informatie gepaard gaan met het opereren met verhoudingen. Om verhoudingen te preciseren, om ze los te maken van de objecten, worden er uiteindelijk getallen bijgehaald: ‘een half’ wordt ‘een tweede’. Moet ‘3 staat tot 4’ beslist wijken voor‘¾’? | |||||||||||||||||||||||||||||||
‘Verhouding’ ingebouwd of aangeleerd?De bal in de andere hoek van de kamer verschijnt op het netvlies van de baby even groot als de knikker vlak voor zijn oog. Maar op het netvlies wordt meer afgebeeld dan bal en knikker: omgevingen van die voorwerpen, die informatie verschaffen omtrent ver-weg en nabij. En al die informatie wordt doorgeseind naar de hersenschors om te worden verwerkt, op een manier die de baby in staat stelt, in strijd met wat op het netvlies wordt afgetekend, de knikker van de bal qua grootte te onderscheiden, voorwerpen, nabij en ver-weg, op wat je noemt hun ware grootte te schatten. 
figuur 6.3
Een reus in het prentenboek, een groot paleis, Klein Duimpje en een mier - ze kunnen allemaal even groot afgebeeld zijn. Juist - maar dan niet op dezelfde bladzij. Op de één kan de reus het hele blad vullen, op de ander Klein Duimpje. Maar wee, als ze bij elkaar komen, want dan moeten hun verhoudingen kloppen. (Of neen - Klein Duimpje kan vlakbij en de reus in de verte afgebeeld zijn, beiden ogenschijnlijk even groot.) Verhoudingen moeten kloppen als het kind plaatjes kijkt: deze bal is van | |||||||||||||||||||||||||||||||
[pagina 71]
| |||||||||||||||||||||||||||||||
de pop en die van het meisje. Vreemd dat het kleine kind als het zelf tekent, verhoudingen niet in acht neemt. Laat het dan vreemd zijn - het is net zo vreemd als het tekenen van poppetjes zonder buik op een leeftijd waarop het kind zoiets van zijn prentenboek niet zou accepteren. Ik ken geen psychologische verklaring voor deze discrepantie. Kinderen spelen met auto's, poppen, huizen op verschillende schaal naast elkaar - het kan moeilijk anders. Maar als het moet, weten ze wát verhoudingsgewijs bij wát hoort en hoe groot zoiets ‘in het echt’ is. Ze weten het operationeel en passief. Op welke leeftijd wordt zoiets bewust en actief? Ik schat dat dit met zes jaar begint: Een rij observaties: Bastiaan (6:1)Ga naar voetnoot1. Na een reeks zonnedagen ziet hij wolken en zegt: ‘Het gaat regenen.’ ‘Neen,’ zeg ik, ‘dit zijn heel hoge wolken, daar komt geen regen van; regenwolken zijn laag en donker.’ Hij: ‘Hoe hoog zijn die wolken?’ Ik (overdrijvend): ‘Tienduizend meter.’ Hij: ‘En hoe hoog zijn regenwolken?’ Ik: ‘Duizend meter.’ Hij: ‘Dus (met de hand op de grond) als wij hier zijn en de regenwolken zó hoog (wijst ongeveer 30 cm boven de grond), dan zijn dat (wijst ongeveer 1 meter boven de grond), geen regenwolken.’ • Verhoudingen worden meetkundig uitgedrukt - met de precisie hapert het nog. Bastiaan (6:0). Tekening achteraf van wat hij in de zandbak heeft gebouwd: tunnels (gestippeld), wegen, bruggen, muren. 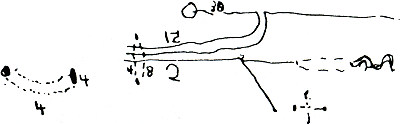
figuur 6.4
Bastiaan drukt op afstanden van een decimeter met parallelle wijsvingers gaten in het zand. De volgende decimeter past hij af door zijn linker wijsvinger in het gat te zetten dat eerst door de rechter gemaakt is. De getallen zijn dus decimeters. • Verhoudingen worden meetkundig en numeriek weergegeven - er wordt precisie betracht. Bastiaan (7:6). De hoogte van een kerktoren (en apart van de klok) wordt viserend gemeten: vergeleken met een stok op een muurtje geplaatst, op een - afgestapte - afstand van de kerk. 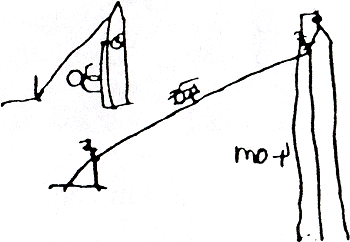
figuur 6.5
| |||||||||||||||||||||||||||||||
[pagina 72]
| |||||||||||||||||||||||||||||||
•‘Verhouding’ als middel om een probleem op te lossen - meetkundig schetsmatig én numeriek met de vereiste precisie. 
figuur 6.6
Coen (8:0) kijkt met zijn vader naar de poster voor de film Orca the killer whale. ‘Wat klopt hier niet,’ vraagt Vader. En Coen, na enige aarzeling: ‘De walvis moet kleiner wezen. Toen we in Engeland waren, zagen we een Orca, die maar zo groot was als twee mannen... Ik herinner me de Orca toen hij uit het water sprong en de oranje bal raakte.’ •‘Verhouding’ om een conflict te beslechten; visuele en mentale situatie numeriek vergeleken met de vereiste precisie. Een derde klas (De groeten van de reus): Uit het spoor, door de hand van de reus op het bord achtergelaten, wordt schattend afgeleid hoe groot de reus is. 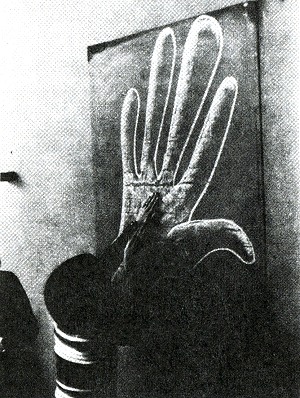
figuur 6.7
•‘Verhouding’ als middel om een probleem op te lossen meetkundig gegeven en numeriek vertaald. | |||||||||||||||||||||||||||||||
[pagina 73]
| |||||||||||||||||||||||||||||||

figuur 6.8
Een onophoudelijke strijd tussen hen die met de liniaal meten en het spoor bijster raken en hen die het mannetje zeven keer in de verticale bruggepijler zien opgaan.
Ik zou dit verhaal kunnen vervolgen tot gevorderde leeftijd toe. Het blijkt dat nog veel ouderen inzichtelijk met verhoudingen blijven werken, waar men breuken van ze zou verwachten. Verhouding is iets oorspronkelijks. Ik laat in het midden hoeveel ervan ‘ingebouwd’ is, voorgeprogrammeerd in de computer van onze hersenschors en hoeveel aangeleerd. Aangeleerd - en dan bedoel ik niet op school, want daar komen verhoudingen, als het dan nog gebeurt, laat aan de orde en bovendien bij wijze van sommetje die de intuïtieve ‘verhouding’ negeren of aan diggelen gooien. Aangeleerd veeleer met prentenboeken en speelgoed die onze grote wereld op schaal nabootsen. Breuken worden meestal op een ander spoor dan dat van de verhoudingen geleerd en dat is jammer. In het onderwijs zouden breuken van verhoudingen kunnen profiteren en verhoudingen van breuken, verondersteld dat die twee leersporen didactisch in elkaar werden geleid. ‘Verhouding’ kan didactisch geenszins gemist worden, al lijkt het puur mathematisch wel zo te zijn. | |||||||||||||||||||||||||||||||
Verhoudingen maken en bepalenVerhoudingen worden allereerst beleefd - we komen er herhaaldelijk nog op terug. Inmiddels iets over hun getalsmatige precisering. | |||||||||||||||||||||||||||||||
[pagina 74]
| |||||||||||||||||||||||||||||||
Jan en Piet moeten knikkers verdelen in de verhouding ‘3 staat tot 2’. (Dit zijn nu eenmaal die verdeelsommen. Waarom ‘3 staat tot 2’? Omdat Jan nog twee broertjes heeft tegen Piet één? Of omdat Jan 9 jaar is en Piet 6?) Hoe gaan ze het doen? Ze hoeven niets van verhoudingen af te weten; ze nemen er telkens 3 respectievelijk 2 van. Of om sneller op te schieten 6 en 4 of 30 en 20. Tot de voorraad op is. (Want de sommen zijn zo, dat het opgaat.) Laat het nu echt gebeuren en met een heel grote voorraad knikkers - ‘ontelbaar veel’. Wel, dan doe je het op het oog (of op het gewicht). Bijvoorbeeld zoals je limonade verdeelt: een glas limonade, bestaande uit ontelbaar veel druppels vloeistof: in twee cilinderglazen met dezelfde middellijn schenken zodat de hoogtes staan als 3 staat tot 2. Je kunt het met limonade doen, maar ook met knikkers. Hoe controleer je zo'n verhouding? Door te meten. En hoe meet je? Met de liniaal. Maar het hoeft niet met de liniaal. En soms kan het niet eens met de liniaal. Een weg kun je meten door hem af te stappen en als je thuiskomt, kun je met de centimeter nagaan hoe lang je stap is. Maar misschien hoeft het niet eens. Als je alleen maar wilt weten welke van twee wegen de kortste is of hoe twee wegen zich verhouden, hoef je je geen zorgen te maken over de maatstaf waar je mee meet. De maatstaf doet er niet toe als het alleen op de verhoudingen aankomt. Hoe verhouden zich de lijnstukken hieronder? Je legt het kleinere zo vaak als het kan op het grotere neer. Het gaat zeven keer, maar er blijft een rest, die de helft van het kleine lijnstuk lijkt te zijn. Dus had je beter met de helft van het kleine lijnstuk als maatstaf kunnen beginnen. Meet je daarmee, dan blijkt het grote 15 en het kleine 2 te zijn. Ze staan tot elkaar als 15 staat tot 2. 
figuur 6.9
Zo eenvoudig gaat het niet altijd. Neem van een vierkant de diagonaal en de zijde. Als de zijde a is berekende de diagonaal volgens Pythagoras op 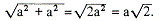 
figuur 6.10
De verhouding diagonaal tot zijde is als √2 staat tot 1. Maar √2 is ‘irrationaal’: er zijn geen gehele getallen m en n te bedenken zo dat √2 = m/n oftewel: Voor geen paar gehele getallen m,n is diagonaal : zijde = m : n. Wel kun je die verhouding willekeurig goed benaderen: 1,414... of met gewone breu- | |||||||||||||||||||||||||||||||
[pagina 75]
| |||||||||||||||||||||||||||||||
ken 3 : 2, of 17 : 12, of 577 : 408, ... - reken maar na: door te kwadrateren krijg je iets dat telkens beter 2 : 1 is. Niet alleen lengtes, maar ook oppervlakten, inhouden, gewichten en tijden kun je verhoudingsgewijs vergelijken. De twee rechthoeken hieronder verhouden zich als 5 staat tot 3, dat wil zeggen zoals hun bases, omdat de hoogten dezelfde zijn. De vierkanten verhouden zich als de kwadraten van hun zijden, dus als 25 : 9, de cirkels als de kwadraten van de stralen, 25 : 9; Hoe groot een cirkel van oppervlakte is, hoef je er niet voor te weten. Nog krasser: teken een willekeurige figuur en beeld hem af in de verhouding 5 : 3. De oppervlakten staan dan in de verhouding 25 : 9. En met ruimtelijke inhouden gaat het op een dergelijke manier, maar dan in de derde macht: 125 staat tot 27 bij de kubussen of bij bollen of bij andere figuren, die in de verhouding 5 : 3 op elkaar zijn afgebeeld. 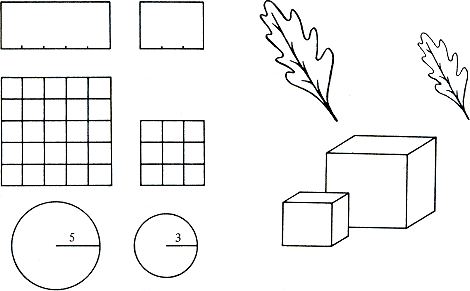
figuur 6.11
Verhoudingen van gewichten - je kunt ze bijvoorbeeld aflezen op de hefboom: als bij evenwicht de armen zich als 3 : 5 verhouden, dan verhouden de gewichten zich als 5 : 3. 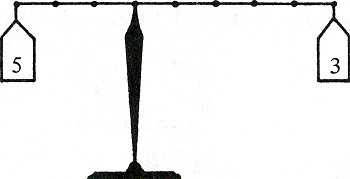
figuur 6.12
Of met een veerbalans: de gewichten verhouden zich als de lengtes waartoe de veer is uitgerekt. | |||||||||||||||||||||||||||||||
[pagina 76]
| |||||||||||||||||||||||||||||||
Met beide methoden vergelijk je feitelijk lengtes als zijnde plaatsvervangers van gewichten. Zo doe je het ook bij tijden - ze staan tot elkaar als de wegen die de wijzer op de wijzerplaat heeft afgelegd. | |||||||||||||||||||||||||||||||
Verhoudingsgetrouw afbeeldenAfbeelden speelde een rol in de voorafgaande voorbeelden. Afbeelden bij wijze van plaatje of symbolisch handelend (het geval van de wolken) of zoals de wijzer die tijd afbeeldt op de kringloop op de wijzerplaat. Al die afbeeldingen zijn verhoudingsgetrouw: De verhoudingen in het origineel worden getrouw weergegeven in het beeld. Het woord verhouding hoeft er niet aan te pas te komen. Je kunt het waarnemen of de verhoudingen kloppen. Of veeleer, het valt je op als iets niet klopt. Het kind identificeert vroegtijdig plaatjes en modellen met de voorwerpen die ze geacht worden voor te stellen, ongeacht de schaal. Plaatjes en modellen op verschillende schaal naast elkaar worden als beelden van hetzelfde object aanvaard. ‘Hoe groot is een walvis in 't echt?’ kan een kind vragen, overtuigd dat de plaat - afgezien van de schaal - de walvis getrouw weergeeft. Wel zijn er ook van die schetsmatig, met één lijn getekende, walvissen, maar zelfs dit verschil tussen fotografisch getrouw beeld en een karakteristieke schets wordt begrepen. Wegingen met een (verticale) veerbalans die Bastiaan (5:6) uitvoerde, werden op een horizontaal en op andere schaal getypt beeld van de veerbalans aangetekend. Bastiaan merkte wel onbeduidende verschillen in de cijfernotatie (l in plaats van 1) op, maar noch het verschil in oriëntatie noch de afwijkende schaal. Het getypte beeld van de veerbalans was immers structureel getrouw. Zonder aarzelen aanvaarden kinderen dat op het schoolbord voorwerpen tien keer zo groot als op het werkblad worden getekend, dat de getallenlijn op het schoolbord 1 dm tot eenheid heeft, tegen 1 cm op het werkblad. Zij aanvaarden naast elkaar getallenlijnen waarbij hetzelfde interval in plaats van de eenheid een tiental of honderdtal voorstelt. Ze zouden echter direct protesteren tegen wijzigingen van de structuur die ingaan tegen de getrouwheid van verhoudingen. 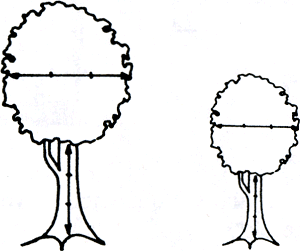
figuur 6.13
| |||||||||||||||||||||||||||||||
[pagina 77]
| |||||||||||||||||||||||||||||||
Wat betekent ‘verhoudingsgetrouw’ bij het afbeelden? Het principe luidt: Wat onderling gelijk is in het origineel moet onderling gelijk zijn in het beeld. Uit dit principe volgt door aan elkaar zetten van lengtes: Wat dubbel (drie keer, ...) zo groot is in het origineel, moet dubbel (drie keer, ...) zo groot zijn in het beeld. Door een blikwisseling volgt hieruit: Wat de helft (een derde, ...) is in het origineel, moet de helft (een derde, ...) zijn in het beeld. Die twee samengesteld levert uitspraken op zoals Wat zich in het origineel verhoudt als 3 :4(als 11 : 7, algemener als p : q), moet zich in het beeld verhouden als 3 : 4 (als 11 : 7, algemener als p : q). Bij afbeeldingen, willen ze verhoudingsgetrouw zijn, moeten de interne verhoudingen van het beeld dezelfde blijven als van het origineel. Met dit verhoudingsgetrouwe afbeelden raken de kinderen vroegtijdig bekend bij schilderijen, kopieën van schilderijen, maquettes. Systematische of toevallige afwijkingen worden geconstateerd, bijvoorbeeld
en dit geschiedt niet door verhoudingen of maatstaven expliciet te maken, maar in formuleringen zoals dit is te smal - namelijk vergeleken bij de hoogte; die figuur is te groot - namelijk vergeleken bij deze; de neus is veel te groot - namelijk vergeleken bij de andere lichaamsdelen. Aanmerkingen ten aanzien van de getrouwheid van verhoudingen, maar zonder dat er uitdrukkelijk van verhoudingen sprake is. 
figuur 6.14
| |||||||||||||||||||||||||||||||
[pagina 78]
| |||||||||||||||||||||||||||||||
Het vereist dieper inzicht in meetkundige relaties om andere gegevens als criteria van verhoudingsgetrouwheid erbij te betrekken: Wat in het origineel een rechte hoek is, moet er in het beeld ook een zijn. 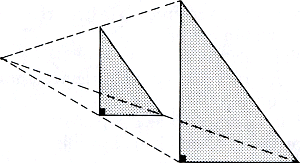
figuur 6.15
Of meer algemeen: Bij het verhoudingsgetrouw afbeelden blijven de hoeken ongewijzigd. Zijn de twee rechthoeken hiernaast verhoudingsgetrouw op elkaar af te beelden? Je kunt het beter zien als je er de diagonalen intekent en op hun hoeken let. 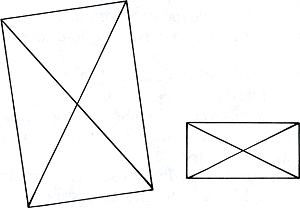
figuur 6.16
Er is echter nog meer aan de hand bij het verhoudingsgetrouw afbeelden. Hoe beeldt ik iets verhoudingsgetrouw af? Daarstraks heb ik het woord ‘kopie’ gebruikt. Kopie kan betekenen: precies eender. Het kan ook betekenen: verkleind of vergroot. En dat kopiëren kan dan geschieden fotografisch, door lichtdruk, als schaduwbeeld of netjes natekenend, eventueel met een pantograaf. Op schaal - zeggen we ook. Wat bedoelen we met ‘op schaal’? 1 : 10 000 staat wel eens op landkaarten en dat wil zeggen: lengte 1 op de kaart is 10 000 in de werkelijkheid. Onder het plaatje van een microbe zou kunnen staan 1000: 1 en dat betekent qua afmetingen 1000 op de plaat is 1 in de werkelijkheid.
Hoe groot is iets in het echt? En zonder uit te kijken bezwijkt de leerling voor de verleiding dat 1 cm op het plaatje in werkelijkheid 1 m of 1 km of 100 000 km is, alsof het niet anders kan.
Er zijn levensgrote statuen maar er zijn ook onder- of bovenmaatse, veelal 2 : 3 of 3 : 2 d.w.z. 2 in het beeld is 3 in het echt of omgekeerd. | |||||||||||||||||||||||||||||||
[pagina 79]
| |||||||||||||||||||||||||||||||
In biologieboeken heb je van die plaatjes - met een voorwerp naast een boomblad om te laten zien, wat de verhoudingen zijn. 
figuur 6.17
Die 1 : 10 000 of 1000 : 1 of 2 : 3 of 3 : 2 van daarstraks zijn schaalverhoudingen oftewel externe verhoudingen in tegenstelling tot de interne die we eerder bekeken. Wel, de verhouding van boomblad tot lucifersdoosje is zo'n interne verhouding binnen het plaatje. De verhouding van boombladplaatje tot echt blad, van plaatje van het doosje tot echt doosje is extern: het is de schaalverhouding. Ziedaar twee manieren om uit te leggen wat ‘verhoudingsgetrouw’ betekent en hoe je verhoudingsgetrouw afbeeldt:
Hoe komt ‘verhoudingsgetrouw’ aan deze twee met elkaar gelijkwaardige aspecten? 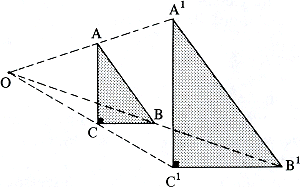
figuur 6.18
| |||||||||||||||||||||||||||||||
[pagina 80]
| |||||||||||||||||||||||||||||||
Maar uit de geldigheid van (1) volgt mathematisch die van (2) en omgekeerd, door verwisseling van de binnentermen. Uit de gelijkheid van de interne verhoudingen volgt dus de standvastigheid van de externe verhoudingen, en omgekeerd. In (2) staat de schaalverhouding van het afbeelden, die alom dezelfde moet zijn. | |||||||||||||||||||||||||||||||
Verhoudingsgetrouw in ruimere zinIn ‘verhoudingsgetrouw afbeelden’ was het afbeelden meetkundig bedoeld. Op het eind van ‘Verhoudingen maken en bepalen’ stond er echter al een toespeling op een ruimere betekenis: de rondlopende wijzerplaat beeldt als het ware de aflopende tijd af op de te doorlopen rand van de wijzerplaat. In gelijke tijden legt de wijzerpunt gelijke wegen af, tenminste als het uurwerk niets mankeert. Het is het principe van wat je noemt eenparige beweging: In gelijke tijden gelijke wegen, dus in de dubbele (drievoudige...) tijd de dubbel (drievoudige...) weg, en weer met blikwisseling: In de halve (derde van de, ...) tijd de halve (een derde van de, ...) weg en uit deze gecombineerd: Als de tijden staan tot elkaar als 3 : 4 (als 11 : 7, als p : q) dan staan de afgelegde wegen tot elkaar als 3 : 4 (als 11 : 7 als p : q). Uiteraard is dit niet bij elke beweging zo. Het is kenmerkend voor de eenparige beweging: de betrekking tussen tijd en afgelegde weg is verhoudingsgetrouw, oftewel de wegen verhouden zich als de tijden waarin ze worden afgelegd. 
figuur 6.19
Nog anders gezegd: de weg was evenredig met de tijd. (‘Reden’ is een ander woord voor verhouding - evenredig is dus ‘dezelfde verhouding hebbende’.)
Het is weer de interne verhouding die hier aan de orde is, weg staat tot weg, tijd staat tot tijd. Maar de externe mag er ook bij te pas komen, dus verhouding ‘weg staat tot tijd’ waar we dan ook de naam snelheid voor hebben: 10 m per sec Het is allemaal hetzelfde, als de beweging maar eenparig is. Dit is dan een nieuwe definitie van eenparigheid en wel door middel van externe verhouding: constante snelheid. Dit was weer een voorbeeld van ‘verhoudingsgetrouw’. En zo zijn er meer. Voor één soort stof verhouden de gewichten zich als de hoeveelheden, of anders gezegd, gewicht en hoeveelheid zijn evenredig - dus aan elkaar gelijkgestelde interne verhoudingen. En als de hoeveelheden in inhoudsmaten zijn gemeten, heet de externe verhouding gewicht per hoeveelheid of ook soortelijk gewicht. | |||||||||||||||||||||||||||||||
[pagina 81]
| |||||||||||||||||||||||||||||||
Of van een zekere handelswaar verhouden de prijzen zich als de hoeveelheden (gewichten), anders gezegd, prijzen en hoeveelheden (gewichten) zijn evenredig. Aan elkaar gelijkgestelde interne verhoudingen - en de externe verhouding verschijnt als prijs per eenheid (per kg). In het geval van de meetkundige afbeeldingen leidt de schaalverhouding tot een onbenoemd getal: de schaalfactor. In de nieuwe voorbeelden, waar verschillendsoortige grootheden met elkaar vergeleken worden, is het een benoemd getal: m/sec., km/uur, g(ram)/cm3, t(on)/m3, f(lorijn)/l(iter), f(lorijn)/kg enzovoort. | |||||||||||||||||||||||||||||||
Grafische visualisering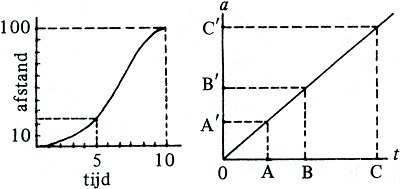
figuur 6.20
Om een beweging te visualiseren maakt men een tijd-weg grafiek. In de grafiek hierboven is de afgelegde weg tegen de tijd uitgezet, bijvoorbeeld na 5 sec 25 m afgelegd. De beweging is niet eenparig: de sprinter moet kennelijk eerst op draf komen en op het eind verslapt hij. Hoe wordt een eenparige beweging grafisch weergegeven? Een rechte lijn. Immers, in gelijke tijden gelijke wegen en dat sluit alleen op elkaar aan bij een rechtlijnige grafiek. Of anders gezegd weg en tijd evenredig, dus OA : OB : OC : ... : AB : AC : BC : ... = OA′ : OB′ : ... A′B′ : A′C′ : B′C′ : ... en dat gaat nét bij een rechtlijnige grafiek op. Of als je het met de standvastigheid van de externe verhouding weg: tijd wilt doen, dan deugt OA′ : OA = OB′ : OB = OC′ = OC = ... A′B′ : AB = ... juist langs een rechte lijn. Deze verhouding, die de steilte van de lijn weergeeft, stijgingsmaat of richtingscoëfficiënt genaamd, betekent voor de tijdweg grafiek de snelheid, uiteraard van eenparige beweging. 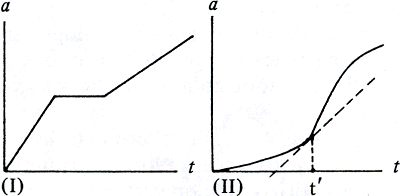
figuur 6.21
| |||||||||||||||||||||||||||||||
[pagina 82]
| |||||||||||||||||||||||||||||||
(Zeker zijn er ook andere, met wisselende snelheid, zoals in grafiek I voorgesteld, of met een snelheid die zelfs continu verandert, zoals in grafiek II; daar valt dan nog een momentele snelheid te definiëren: op het tijdstip t bepaald door de stijging van de raaklijn aan de grafiek. Maar dit is een ander chapiter, dus tussen haakjes.) Zoals de afstand tegen de tijd kan men het gewicht tegen het volume uitzetten, weer een rechtlijnige grafiek, waar de stijgingsmaat dan als soortelijk gewicht is te interpreteren - hieronder grafieken van twee stoffen, de ene soortelijk dubbel zo zwaar als de ander. En net zo kan je prijsgrafieken maken, diverse voor verschillende produkten. 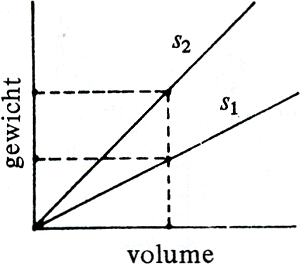
figuur 6.22
| |||||||||||||||||||||||||||||||
Functie, grafiek en afbeeldingAls iets beweegt, zeg je ook wel de weg is een functie van de tijd. Als je mikt is het trefpunt een functie van de richting van mikken. De prijsindex als functie van de tijd, de temperatuur in De Bilt als functie van de tijd zie je wel eens door een grafiek gevisualiseerd. 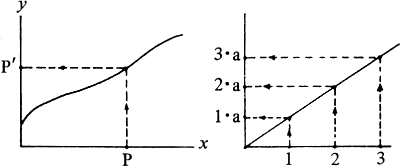
figuur 6.23
y is functie van x betekent aan een waarde van x beantwoordt er een van y, en dat kun je per grafiek ook interpreteren alsof je de horizontale as op de verticale afbeeldt en wel door middel van een pijl die bij de grafiek gebroken wordt: als het punt P op de horizontale as loopt, dan loopt zijn beeldpunt P' mee op de verticale as. Zo'n afbeelding is in het algemeen niet verhoudingsgetrouw. Wil dit wel het geval zijn, dan moet de grafiek een rechte lijn (door het snijpunt van de assen) zijn. Een functie die door zo'n grafiek wordt voorgesteld, heet dan ook een lineaire functie. Zo'n verband wordt door y = ax met zekere vaste a beschreven. De a is ons welbekend. Vatten we de lineaire functie als (verhoudingsgetrouwe) afbeelding van horizontale op verticale as op, dan is a de schaalfactor, oftewel a : 1 = 2a : 2 =... de schaalverhouding van de afbeelding. In | |||||||||||||||||||||||||||||||
[pagina 83]
| |||||||||||||||||||||||||||||||
plaats van ‘verhoudingsgetrouw afbeelden’ kan men ook zeggen lineair afbeelden, d.w.z. door middel van een lineaire functie. | |||||||||||||||||||||||||||||||
Naar verhoudingWe begonnen de uiteenzetting met het verhoudingsgetrouw afbeelden. In het begrip hiervan kun je het ver brengen zonder ooit het woord ‘verhouding’ in de mond te nemen, dank zij de visualisering. Andere contexten vereisen vroegtijdig verbalisering, zij het dan niet direct met het begrip verhouding, maar wel met het begrip naar verhouding. Als mentaal object is dit tegen het einde van de kleuterleeftijd aanwezig. Deze chocola is zoeter omdat er - naar verhouding - meer suiker in zit. Een vlo kan - naar verhouding - hoger springen dan een mens. In de expliciete formulering kan het ‘naar verhouding’ ontbreken, ook al is duidelijk dat het op die plaats bedoeld is. De termen naar verhouding meer, minder, evenveel kunnen van grof kwalitatief tot precies kwantitatief bedoeld zijn: speciaal bij ‘meer’ of ‘minder’ kunnen schattingen bedoeld zijn, die door veel, zeer veel, iets verfijnd kunnen worden. Bij ‘naar verhouding’ ontbreekt een relatieterm, die vanzelfsprekend kan zijn of expliciet wordt toegevoegd, bijvoorbeeld naar verhouding tot het aantal inwoners zijn er in Nederland meer fietsen dan in de Bondsrepubliek Duitsland. Laten we een didactische sequentie aanduiden: Welk bloembed is mooier? 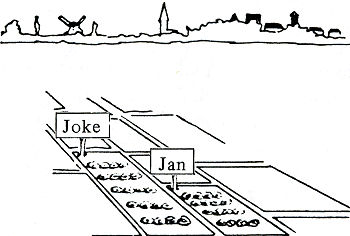
figuur 6.24
Hoe beslecht je zo'n strijd? Je vraagt: In welk opzicht staan er minder bloemen op Jokes bed? | |||||||||||||||||||||||||||||||
[pagina 84]
| |||||||||||||||||||||||||||||||
Verhoudingsgewijs... in verhouding tot wat? Relatief... ten opzichte waarvan?
Je moet dus beide bedden even groot maken. En wat doe je dan met de bloemen?
Dus, bij het vergroten of verkleinen de interne verhoudingen aanhouden.
Dus de externe verhoudingen aanhouden.
De externe verhouding ‘bloemen per vierkante meter’ wordt gepreciseerd.
Een andere sequentie: Waar krijgen de koeien meer eten? 
figuur 6.25
De interne verhouding.
De externe verhouding. Maar hoe zie je dat De Groots weiland maar een beetje groter is?
De externe verhouding. We merken een sequentie van niveaus op. | |||||||||||||||||||||||||||||||
[pagina 85]
| |||||||||||||||||||||||||||||||
Van grof kwalitatief tot precies kwantitatief kunnen hierbij een aantal stadia worden doorlopen waarbij in laatste instantie naar gelang van het onderwerp interne en externe verhoudingen over relatieve ordening beslissen. Opgaven waarin deze activiteiten beoefend worden, kunnen een visueel karakter hebben:
Maar ook andere zintuigen kunnen erbij worden betrokken:
| |||||||||||||||||||||||||||||||
Andere visualiseringenBij het meetkundig afbeelden is verhoudingsgetrouwheid vanzelf gevisualiseerd. Grafieken zijn een middel om verhoudingsgetrouwheid te visualiseren, al is die op zichzelf niet-meetkundig gegeven. Maar verhoudingsgetrouwe beelden kunnen ook worden gebruikt om de verhoudingen zelf te visualiseren. De voornaamste middelen van visualisering van verhoudingen zijn histogrammen en beeldstatistieken, sectordiagrammen. Voorbeeld voor het eerste: 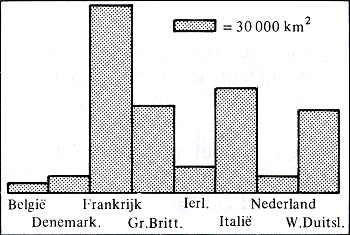 OPPERVLAKTE van een aantal E.E.G.-landen
figuur 6.26 | |||||||||||||||||||||||||||||||
[pagina 86]
| |||||||||||||||||||||||||||||||
De EEG-landen worden wat hun oppervlakte betreft, door rechthoeken van gelijke basis en van met de oppervlakte evenredige hoogte weergegeven, die als in een histogram naast elkaar zijn geplaatst. (Zie figuur 6.26.) De inwonertallen door rijen menselijke figuren (elk bijvoorbeeld drie miljoen vertegenwoordigend, zie figuur 6.27). Beide beelden kunnen zo gecombineerd worden, dat de menselijke figuren telkens in de rechthoeken worden geplaatst (figuur 6.28) om de uiteenlopende dichtheid van bevolking (verhouding van inwonertal tot oppervlakte) te visualiseren. 
figuur 6.27
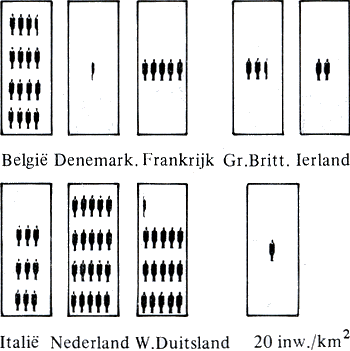 DICHTHEID BEVOLKING van een aantal E.E.G.-landen
figuur 6.28 Voorbeeld van het tweede: Een cirkel in sectoren opgedeeld beantwoordende aan en wat oppervlakte aangaat evenredig met de gebruikscategorieën van de bodem van een land
Dergelijke visualiseringen zijn verhoudingsgetrouwe afbeeldingen, waarbij echter op andere verhoudingen dan die van afstanden van puntenparen wordt gelet, in het onderhavige geval op verhouding van oppervlakken van landen, inwonertallen, bodemoppervlakken naar gebruikscategorieën, aan de ene kant en oppervlakken van vlakke figuren aan de andere kant. | |||||||||||||||||||||||||||||||
NormeringHet complex van technieken, onjuiste toepassing van technieken, door die technieken bepaalde of liever niet bepaalde attitudes, dat ik met het woord ‘normering’ aanduid, wil ik door een aantal voorbeelden introduceren: Als we ons de aarde als speldeknop denken (1 mm middellijn), verschijnt de zon als een bol met middellijn 10 cm op een afstand van 10 m. De maatstafreductie dient om krasse verhoudingen te visualiseren; men kiest een vertrouwde eenheid als uitgangspunt, hoe groot de schaal is, doet er weinig toe. | |||||||||||||||||||||||||||||||
[pagina 87]
| |||||||||||||||||||||||||||||||
Als we de ontwikkeling van het leven op aarde zich in een etmaal laten voltrekken, is de oermens een minuut geleden opgetreden en de menselijke beschaving een seconde geleden begonnen. Het lijkt veel op het eerste voorbeeld: nu een tijdschaalreductie, die eventueel door een lineaire tekening kan worden geïllustreerd. De eenheid ‘dag’ is hier voor de grootste component gekozen, terwijl in het eerste voorbeeld met de speldeknop was begonnen. De voorbeelden Een op de vijf kinderen die geboren worden, is een Chinees, een op de vier auto 's is een Fiat tonen een voorkeur voor verhoudingen die als ‘één op de...’ zijn genormeerd. Een recept ‘bœuf à trois moutardes’ voor vier personen... - als maaltijdeenheid wordt voor recepten vaak 4 gekozen, in veel gevallen zal dit omrekeningen besparen. Het is echter riskant om bijvoorbeeld bij bakprocedures zonder meer op evenredigheden te vertrouwen. De zuiverheid van drink- en zwemwater wordt aangegeven met zoveel gram zout in één liter of zoveel colibacteriën in één cc, waarbij de hoeveelheden die gedronken worden of waarin gezwommen wordt van geheel andere afmetingen zijn en de feitelijke onderzochte hoeveelheden weer van andere, maar dit blijft geheel buiten beschouwing. De afvalproduktie wordt met zulk een vage eenheid als een inwonerequivalent gemeten, dat alleen maar dient om de produktie van huishoudingen en industriële bedrijven te schatten en er een belasting aan te verbinden. De kracht van nucleaire ontploffingen wordt in kilotonnen TNT gemeten, een merkwaardige normering die veeleer dient om nucleaire bommen onderling dan met conventionele springstof te vergelijken. Als de kosten van levensonderhoud in 1965 op 100 worden gesteld, komen ze in 1975 op 147 - een voorbeeld voor de veel gebruikte indexcijfers, waarbij bij voorkeur van een basis 100 wordt uitgegaan. In andere gevallen wordt het gemiddelde als maat genomen en gelijk aan 100 gesteld, bijvoorbeeld bij het I.Q.: de gemiddelde score in een bepaalde populatie (van bepaalde leeftijd) wordt op 100 gesteld om andere scores hiermee te meten. Die 100 sluit aan de ene kant goed aan bij het tientallig stelsel, en bewerkt aan de andere kant dat desniettemin tientallige breuken zoveel mogelijk vermeden worden. Dat het 100 en niet bijvoorbeeld 1000 is, komt van het percentrekenen. In het traditionele rekenonderwijs waren percent en rente nauw aan elkaar geliëerd. Dit is niet van ouds zo geweest; rente werd veeleer in ‘één op de...’ uitgedrukt (evenals bij belastingen die als tiende penning, dertiende penning, enzovoort werden geheven). Pas met de decimalisering van het geld werd het rente-percent rekenen effectief. De meest uitgebreide toepassing van het percentrekenen is tegenwoordig die bij het vergelijken van delen van een geheel: het geheel wordt 100 gesteld, om er de delen in uit te drukken. De bedoeling hiervan is verschillende opdelingen vergelijkbaar te maken, waarbij de vergelijking nog door visualisering gesteund kan worden, bijvoorbeeld door middel van sectordiagrammen. De behoefte aan dit vergelijkbaar maken van gegevens in de vorm van compositiestaten is tegenwoordig de sterkste | |||||||||||||||||||||||||||||||
[pagina 88]
| |||||||||||||||||||||||||||||||
motivering voor het percentrekenen; bovendien is het percentrekenen hier een werktuig dat zich vanzelf aanbiedt, zodra het idee is opgevat dan ten behoeve van vergelijkbaarheid de totalen uniform genormeerd moeten worden, dus niet als Nederland even groot was als de Bondsrepubliek, noch als de Bondsrepubliek even groot was als Nederland, maar stel de oppervlakte (het inwonertal) van beide op 100 (ook wel eens 1000), dan... Dit normeren sluit ook gevaren in zich: men vergeet waar de genormeerde gegevens vandaan komen en dat er in verschillende gevallen ook van verschillende schaalfactoren sprake kan zijn:
Subtieler en tevens gevaarlijker is de uitwerking van het vergeten van de ongenormeerde gegevens doordat, bijvoorbeeld bij statistieken, tevens vergeten wordt hoe nauwkeurig de genormeerde gegevens zijn: Eén op de twee, of 50% kan uit een totaal van net twee verkregen zijn of als een min of meer ruwe schatting uit een totaal van duizend of een miljoen.
Een typisch geval uit het jongste verleden, de koopsom-polisaffaire: 38 leden van de Tweede Kamer en 8 kabinetsleden zouden zich verrijkt hebben of zich hebben trachten te verrijken door door de mazen van de belastingnetten te glippen - getallen die klinken alsof de zegsman die het moest weten, hun namen kende en hun neuzen had geteld. Op zeker ogenblik merkte iemand op dat 38 respectievelijk 8 net (eventjes afgerond) een vierde was van 150 respectievelijk 33 d.w.z. van het totaal aantal Tweede-Kamerleden respectievelijk kabinetsleden. Wel - kon je concluderen - de man die het moest weten, had vermoedelijk gezegd: een kwart (of 25%) van de Tweede Kamer en van het Kabinet heeft een koopsompolis - een uitspraak die klinkt of je er met de pet naar gooit. Het is de vraag of zo'n aantijging zo serieus zou zijn genomen om hem door een commissie van wijze mannen en vrouwen te laten uitzoeken, als | |||||||||||||||||||||||||||||||
[pagina 89]
| |||||||||||||||||||||||||||||||
er van een kwart (of 25%) sprake was geweest. Maar iemand die het verhaal doorgaf, of degene die het bekend maakte, vertaalde die 25% in het netjes uitgerekende kwart van de zittende Kamer en het zittende Kabinet, dus in de cijfers 38 en 8, die een veel grotere betrouwbaarheid claimen dan het losjes opgeven van ‘een kwart’. Wat is er dan fout aan, als je een kwart van de Tweede Kamer en het Kabinet vertaalt in 38 en 8? Immers de berekening klopt toch. En toch is het fout - een vertaalfout. Net zo'n vertaalfout als wanneer je in Shakespeare's King Lear ‘every inch a king’ de ‘inch’ vertaalt met 2,54 cm. Een ander voorbeeld waar het mis is met de evenredigheid: Een goede dobbelsteen hoort één op de zes keer een zes te vertonen. Is dat hetzelfde als twee op de twaalf keer, als 100 op de 600 keer? Wel, je weet al dat het niet precies één op elke zes keer gebeurt - was dat het geval dan was de aardigheid er af. De kans dat het precies één op de zes keer gebeurt is maar 40%. De kans dat het precies twee op de twaalf keer gebeurt is nog minder, maar 28%. En dan gaat het snel bergafwaarts: De kans dat het precies 10 op de 60 keer gebeurt is al zo belachelijk klein, dat je hem gerust kunt verwaarlozen. Maar als je bij een dobbelsteen zegt ‘één op de zes keer een zes’ dan bedoel je dat ook niet als precies ‘één op elke zes keer’. Je bedoelt het als een soort gemiddelde - de kans bijvoorbeeld dat er pas bij 12 keer gooien de eerste zes komt is nog steeds 2%. En de les: Het is niet allemaal evenredigheid wat de klok slaat. Je moet met verhoudingen en evenredigheden verstandig opereren. Maar dán kun je er ook veel mee doen. | |||||||||||||||||||||||||||||||
Terug- en vooruitblikMen denkt wel dat getal de eerste wiskundige uiting in de ontwikkeling van de individuele mens en van de mensheid is en was. Zou u niet na lezing van dit opstel aan verhouding de prioriteit toekennen? En waarom wordt het onderwerp dan in het onderwijs zo verwaarloosd? Hoeveel benaderingswijzen ervoor zijn, en hoe goed die doordacht kunnen en moeten worden is hier uiteengezet: denk alleen maar aan ‘naar verhouding’, aan ‘interne en externe verhouding’ en aan ‘verhoudingsgetrouw’. Wat betekent ‘verhouding’ voor het ‘vooruitwijzend leren’ van opstel 4? Wat vindt u van hetgeen hier over verhouding is gezegd en van de contexten waarin verhouding is geplaatst in reken-wiskundemethoden terug? Om het aanvankelijk schattende ‘naar verhouding’ te preciseren, moet men meten. Hieraan is het volgende opstel gewijd. |


