|
| |
| |
| |
5. Oppervlakte als verschijnsel benaderd
1. Naar het meten toe
1.1
Hoe meet je oppervlakten? Of allereerst: hoe méét je? Oppervlakte lijkt iets van de bovenste plank, lengte maal breedte, iets waarbij verondersteld wordt dat je al kunt vermenigvuldigen - zo lijkt het.
Dus: hoe meet je? Hoe meet je wát?
Lengte lijkt het eenvoudigst om te meten - naar gelang van de gerichtheid noem je het ook wel breedte, hoogte, diepte, dikte, maar laten we het bij de term lengte laten. Gewicht lijkt ingewikkelder, hoeveelheid vloeistof idem, maar met moderne weegschalen en met maatglazen wordt zoiets praktisch tot lengtemeting herleid. Snelheid lijkt nog ingewikkelder, maar de snelheidsmeter van een auto maakt ook dit gemakkelijk.
Meten is het antwoord op vragen als: hoe lang, hoe zwaar, hoeveel, hoe snel? Vragen, die nogal ingewikkelde meetprocedures vereisen. Maar je kunt eenvoudiger beginnen. Aan het meten gaat als meer fundamentele werkzaamheid het vergelijken vooraf: twee zaken zijn even lang, zwaar, veel, snel. Of: de ene is langer, zwaarder, meer, sneller, dan de andere.
En dan hoef ik nog lang niet aan vragen te denken als: hoevéél langer, zwaarder, meer, sneller?
Of: hoeveel keer zo lang, zwaar, veel, snel?
| |
1.2
Het vergelijken gaat aan het eigenlijke meten vooraf. Maar wat heb ik aan het vergelijken als ik niet tevens meet? Heel veel. Je kunt er zonder moeite voorbeelden voor bedenken. Bijvoorbeeld: voorwerpen rangschikken volgens lengte, gewicht, hoeveelheid; sportprestaties volgens snelheid. Maar er is een nog fundamenteler motief om lengte, gewicht, hoeveelheid, te vergelijken, namelijk het eerlijk verdelen van, zeg: dropveter, koek, limonade.
Je begint zo maar te verdelen, zeg: in drie porties, op goed geluk; van wie meer heeft neem je iets af en je verdeelt het weer, en zo ga je door tot elk evenveel heeft. Dit eerlijk verdelen vereist dat je kunt vergelijken: heeft er één meer, hebben ze nú evenveel?
| |
1.3
Om te vergelijken heb je twee relaties nodig: equivalentie en orde.
Een deel is minder dan het geheel - dat schept een orde, maar daarmee kom je er niet. Het gaat ook om het vergelijken qua lengte, gewicht, hoeveelheid, van voorwerpen die niet het ene deel van het andere hoeven te zijn. Om te kunnen vergelijken, moet je voor voorwerpen plaatsvervangers kunnen aanwijzen, die evenveel waard zijn. Wiskundig gesproken: equivalent.
Hoe vergelijk je de in figuur 5.1 aangeduide lengten? Je brengt de voorwerpen bij elkaar; dat helpt als ze rechtlijnig zijn - wie buiten de ander uitsteekt, is langer. Zijn ze geknikt of gekromd, dan moet je ze eerst recht
| |
| |

figuur 5.1
trekken, alsvorens ze bij elkaar te brengen en te vergelijken, of je moet het recht voorwerp om het geknikte of gekromde heenbuigen.
Zodoende hebben we met twee lengtebehoudende bewerkingen kennisgemaakt. Voorwerpen worden qua lengte vergeleken door ze:
| - | als vaste lichamen te verplaatsen (liniaal); |
| - | als buigzame lichamen te buigen (duimstok, meetlint, touwtje). |
Als derde voeg je er nog aan toe:
| - | het knippen en plakken; een bewerking, waarbij je onderdelen kunt uitwisselen, terwijl het voorwerp even lang blijft. |
| |
1.4
Hóe lang? - was nog steeds niet aan de orde. Hoe kan een antwoord op die vraag luiden? Bijvoorbeeld: drie stappen. Maar als het om een rechte afstand gaat, moeten het wel stappen recht achter elkaar zijn.
Voor je aan het meten toe bent, moet je weten hoe je maatstaven aan elkaar zet. Er is een samenstellen van voorwerpen qua lengte, gewicht, hoeveelheid, een optelling die nog niet numeriek hoeft te worden opgevat; een ‘samen’ zoals de uitspraken:
| - | a en b samen zijn even lang (zwaar, veel) als c; |
| - | a en b samen zijn langer (zwaarder, meer) dan c. |
| |
1.5
We resumeren: aan het meten gaat vooraf het kennen van relaties van equivalentie, orde en een optelling.
En dan kun je trachten te meten. Een standaardvoorwerp e wordt gekozen: een maatstaf of eenheid. Om een voorwerp a te meten kijk je hoe vaak e erin opgaat, dat wil zeggen: je telt met e equivalente voorwerpen zo vaak op tot a uitgeput is. Lukt het, dan is a met e gemeten; a is een veelvoud van e. Lukt het niet, dan moet er iets met de rest gebeuren: e wordt door een deeleenheid vervangen, zeg: een tiende ervan, waarmee je de rest tracht uit te putten, om a in helen en tienden als veelvoud van e uit te drukken. Lukt het weer maar op een rest na, dan zet je het proces met honderdsten, duizendsten, ... voort, tot je er genoeg van hebt. Zo gaat het tientallig, maar let wel: het mag ook anders.
Bij de drie principes is er een bijgekomen: onbeperkte deelbaarheid.
Meten is uitputten met een eenheid of delen ervan.
De maat van een voorwerp is een positief veelvoud van een eenheid.
| |
1.6
Nu we eindelijk aan meten en maat toe zijn, laten we voor een ogenblik de te meten voorwerpen (bijvoorbeeld lange voorwerpen) door hoofdletters aanduiden en hun maat (bijvoorbeeld de lengte) door het functie-
| |
| |
symbool m. Dus: m (A) zou de maat van A (de lengte van stok A) zijn. Ons rest nu de principes van vroeger met de maat m te confronteren:
| - | equivalentie: als A en B equivalent zijn is m (A) = m (B); |
| - | orde: als A minder is dan B, dan m (A) < m (B); |
| - | optelling: is C samengesteld uit A en B, dan m (C) = m (A) + m (B); |
| - | deelbaarheid: bij een voorwerp A is er voor elk natuurlijk getal n een voorwerp B zodat m (B) = 1/n m (A). |
| |
1.7
Oppervlakte kwam onder onze voorbeelden nog niet voor, maar alles wat aan de orde was, geldt ook voor oppervlakte. Alleen komt het hier veel gevarieerder en geschakeerder voor de dag. Oppervlakte is voor het meten een rijkere context dan lengte, gewicht, hoeveelheid. En daardoor kan oppervlakte, didactisch gezien, een even goed uitgangspunt op de weg naar het meten toe zijn als lengte - of misschien zelfs een betere. Tenminste, als je als leerproces een weg ernaar toe wilt bewandelen en niet plompverloren wilt starten met: oppervlakte = lengte maal breedte. De weg naar oppervlakte kan beginnen vóór de wetenschap van het ‘maal-nemen’ aan de orde is, zelfs vóór lengte en breedte.
| |
1.8
Oppervlakte is een grootheid om voorwerpen mee te meten van een verscheidenheid die gevarieerder lijkt dan bij welke andere grootheid ook:
| - | een vel of rol papier of karton; |
| - | een plaat hout of hardboard; |
| - | een rol of coupon stof; |
| - | een huid leer; |
| - | een voetbalveld of zwembad; |
| - | een stuk bouwland of bos; |
| - | een perceel om te bebouwen; |
| - | het territoir van een staat en zijn onderdelen naar aard van gebruik; |
| - | het bronnengebied van een rivier; |
| - | de spiegel van een meer of zee; |
| - | een muur om te schilderen of te pleisteren; |
| - | een vloer om te beleggen of te parketteren; |
| - | een kantoorvloer of raamoppervlak om schoon te maken; |
| - | een straat om te plaveien of te asfalteren; |
| - | een dak om te dekken; |
| - | een weiland om te maaien; |
| - | een akker om te ploegen en te bezaaien, of te beplanten; |
| - | een huidoppervlak om zijn warmteuitwisseling te kennen; |
| - | een huidoppervlak om nauw of luchtig te bekleden; |
| - | het bladerenoppervlak van een bos om zijn verdamping en gasuitwisseling te kennen. |
En verder:
| - | oppervlakken van meetkundige figuren, vlakke, afwikkelbare en niet-afwikkelbare, al dan niet in formules uitdrukbare;
als zodanig van belang, of als hulpmiddel om lengten in andere uit te drukken (zoals bij de stelling van Pythagoras). |
| |
| |
| |
1.9
Net als voor andere grootheden is voor het meten van oppervlakte vereist: equivalentie, orde, optelling, onbeperkte deelbaarheid.
En meten is in laatste instantie: uitputten met een eenheid of delen ervan. Maar net als bij de andere grootheden vindt dat meten pas aan het einde van het leerproces plaats. Net als bij andere grootheden vloeit de equivalentie voort uit: verplaatsingen, buigingen, knip-plaktransformaties.
Maar vergeleken bij lengte vertoont oppervlakte een grotere geschakeerdheid, een grotere rijkdom, wat de aard van optellen en knip-plaktransformaties betreft.
Het samenstellen van lange voorwerpen is, op verwisseling van onderdelen na, ondubbelzinnig bepaald, terwijl je voorwerpen waaraan een oppervlakte wordt toegekend, op een zeer gevarieerde manier kunt samenstellen.
Knip-plakprocedures kunnen vlakke voorwerpen onherkenbaar veranderen - tangrampuzzelaars weten er alles van.
| |
2. Oppervlakte en het lastige ervan
2.1
Het begint dus ook bij oppervlakte weer met het vergelijken: wie is groter, wie kleiner? Bij figuur 5.2 is het zó te zien:
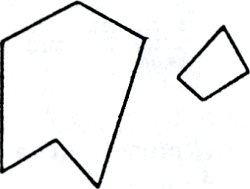
figuur 5.2

figuur 5.3
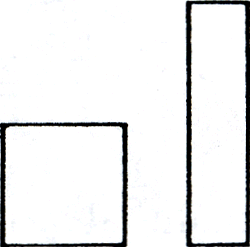
figuur 5.4
De ene figuur is binnen de andere te plaatsen. Bij figuur 5.3 lukt het niet direct, maar wel nadat de smalle figuur in een aantal stukken is geknipt. Figuur 5.4 lijkt moeilijker; het is verleidelijk naar lengte en breedte te kijken, maar met knippen en plakken kan het ook lukken. Tenslotte: hoe moet het met figuur 5.5? Met lengte maal breedte lukt het niet. Toch hebben ze vast
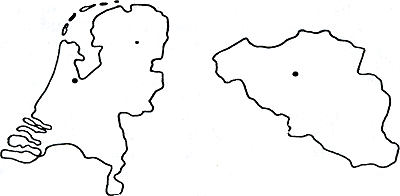
figuur 5.5
| |
| |
en zeker een oppervlakte, want het zijn plaatjes van Nederland en België op schaal - landen die volgens de aardrijkskundeboeken zo en zoveel vierkante kilometers meten, en vierkante kilometers is een oppervlaktemaat; een vierkant van 1 km lang en breed.
Dat is dus een eenheid om oppervlakte mee te meten: een vierkant met een bepaalde zijde. Van zo'n eenheid hebben we equivalente representanten nodig; congruente vierkanten, en die vinden we het gemakkelijkst in een rooster, zeg: van millimeterpapier - roostervierkanten van cm2, onderverdeeld elk in 100 mm2 en, als u het zich kunt verbeelden, in honderdsten, tienduizendsten, ... ervan. Daar leg je de plaatjes van figuur 5.5 op en dan ga je tellen hoeveel hokjes in elk van de plaatjes zitten (figuur 5.6).

figuur 5.6
We zijn dus al haast bij het meten aangeland. Ook de nauwkeurigheid van de meetprocedure laat zich verantwoorden. We benaderen de gegeven figuur:
| - | van binnen; dat wil zeggen: als som van de roostervierkantjes, die erin zitten; |
| - | van buiten; dat wil zeggen: als som van de roostervierkantjes, die er iets mee gemeen hebben. |
Naar mate van roosterverfijning verbeteren de benaderingen van binnen en van buiten. Groeien ze op den duur naar elkaar toe om uiteindelijk iets te bepalen dat terecht ‘oppervlakte van de figuur’ mag heten? Een lastige vraag, waar je in alle eerlijkheid ja noch nee op kunt zeggen. Het hangt van de figuur af. Om de nieuwsgierige gerust te stellen: voor wat je gewoon bent meetkundige figuren te noemen, luidt het antwoord: ja. En om niet te gauw gerust te stellen: dit antwoord vereist een bewijs dat niet gemakkelijk is.
Ziedaar punt nummer één, waarom oppervlakte een lastpak kan zijn.
| |
2.2
Het kan nog lastiger. We hebben de plaatjes van figuur 5.5 zo maar op het rooster in figuur 5.6 neergelegd. Door de betrokken hokjes te tellen wordt de oppervlakte benaderd. Maar wat nu, als je de plaatjes anders neerlegt? Komt er dan hetzelfde uit - ik bedoel met voortgaande verfijning van het rooster?
Ik zeg iet iets eenvoudiger: teken een vierkant van drie-bij-drie rechtop-
| |
| |
staande op het rooster. Verschuif hem evenwijdig en tel weer de hokjes. Er zal wel hetzelfde uitkomen, zeker bij gedurige verfijning. Maar ga hem nu draaien zodat hij schuin op het rooster ligt (figuur 5.7). Klopt het dan ook nog? De twee vierkanten, de rechtopstaande en de schuine, zijn congruent, ze zouden dezelfde oppervlakte moeten hebben - het hokjes tellen zou op den duur hetzelfde moeten opleveren.
Ter geruststelling: het is ook zo. En om u weer niet te gauw gerust te stellen: je moet er moeite aan besteden om het gemakkelijk te bewijzen en zelfs dat gemakkelijke bewijs is nogal moeilijk.
Ziedaar punt nummer twee, waarom oppervlakte een lastpak kan zijn.

figuur 5.7
| |
3. Moet het zo lastig?
3.1
Moet dit nu zo - een vierkant als maatstaf om oppervlakten te meten of ook maar te vergelijken? Wel, zo iets is - en dan in roostergedaante - geschikt om onregelmatig kromlijnig begrensde figuren uit te putten, maar voor rechtlijnig begrensde of regelmatige figuren lijkt het een averechtse procedure.
Twee krasse voorbeelden:
| - | een vierkant, in twee congruente delen verdeeld, geeft aanleiding tot een deelfiguur, die direct (zonder uitputten met vierkantjes) als helft van het vierkant herkenbaar is;

figuur 5.8
|
| - | een cirkelschijf is kennelijk beter met regelmatige veelhoeken dan met vierkantjes uit te putten. |
Het eerlijk verdelen laat zich bij alle grootheden tot een numerieke deling terugbrengen, doordat het te verdelen voorwerp gemeten wordt. Het ligt voor de hand deze weg in te slaan als de meetprocedure eenvoudig genoeg is, zoals meestal het geval is bij lengten, gewichten, tijden, vloeistofhoeveelheden.
Het meten van oppervlakten (en vaste inhouden) is meestal ingewikkelder en kan zelfs heel moeilijk zijn. Het ligt dan voor de hand te profiteren van een eventuele meetkundige structuur van het te verdelen object. Er zijn tal
| |
| |
van manieren om een vierkant, een cirkelschijf, een cilinderoppervlak, in drie congruente delen te verdelen. Elke manier levert ook een eerlijke verdeling van de oppervlakte op. Vertoont het te verdelen voorwerp minder of geen meetkundige structuur, dan zal men veelal de eerlijke verdeling bij wijze van schatting prefereren boven een ingewikkelde meetprocedure.

figuur 5.9
| |
3.2
Het hoeft dus niet per se zo moeilijk - met starre roosters en benaderingen. Rechtlijnig begrensde figuren kunnen we best met knip-plakprocedures aan.
We beginnen met rechthoeken. De formule:
oppervlakte = lengte maal breedte,
(het is toch maar een definitie) laat zich rechtvaardigen door knip-plakprocedures en congruente driehoeken.
Immers (figuur 5.10), door van de congruente grote driehoek pqc en pqc′ de paren congruente kleine driehoeken pob, qoa en poa′, qob′ af te trekken, zie ik van de resterende rechthoeken:
opp oacb = opp oc′c′b′.
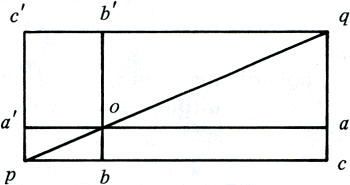
figuur 5.10
aan de andere kant:
oa : oa′ = ob′ : ob.
Oftewel:
oa·ob = oa′·ob′.
Dus: twee rechthoeken hebben dan en slechts dan dezelfde oppervlakte als ze in de produkten van de zijden overeenstemmen.
Het produkt van de zijden kenmerkt de oppervlakten van rechthoeken. Moeten rechthoeken dus niet alleen worden vergeleken maar ook gemeten, dan dient ‘lengte maal breedte’ zich als maat aan en deze maat - oppervlakte genaamd - voldoet aan wat we in 1.6 als eisen formuleerden:
| - | equivalentie: voor congruente rechthoeken a en b is opp a = opp b; |
| - | orde: zit rechthoek a in rechthoek b, dan is opp a < opp b; |
| |
| |
| - | optelling: zet je twee geschikte rechthoeken a, b langs een zijde zo aan elkaar dat weer een rechthoek c ontstaat, dan is opp c = opp a + opp b;
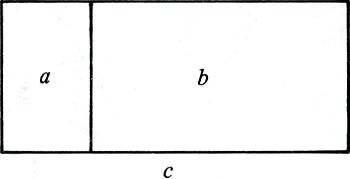
figuur 5.11
|
| - | deelbaarheid: deel je een zijde van rechthoek a in n gelijke delen, dan ontstaat hierop een rechthoek b zodat opp b = 1/n opp a. |
| |
3.3
Met knip-plakprocedures zijn willekeurige veelhoeken qua oppervlakte tot rechthoeken te herleiden.
Allereerst de parallellogrammen. Figuur 5.12 laat dien hoe het parallellogram
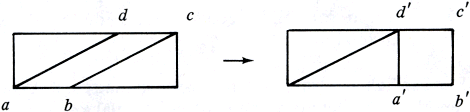
figuur 5.12
abcd door aanplakken en weer wegknippen van driehoeken tot de rechthoek a′b′c′d′ herleid wordt.
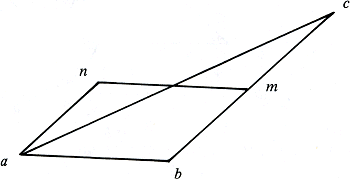
figuur 5.13
Dan de driehoeken (figuur 5.13): abc herleid tot het parallellogram abmn door wegknippen en toevoegen van een driehoek. Tevens blijkt hieruit dat elke driehoek in elke andere met gelijke basis en hoogte kan worden omgezet door plak- en knipprocedures.
Tenslotte kan evenzo een n-hoek (abcde) tot een (n-l)-hoek (abce′) worden herleid, om uiteindelijk bij een driehoek te belanden.
Het essentiële van deze beschouwing is, dat voor veelhoeken gelijkheid en vergelijking van oppervlakte door knip-plakprocedures, zonder tussenkomst van roosters en benaderingsprocessen, kan worden gedefinieerd. Elke veel-
| |
| |
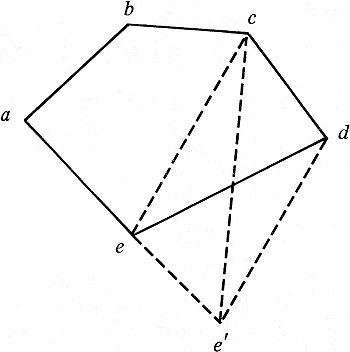
figuur 5.14
hoek is qua oppervlakte tot een rechthoek en nog wel met gegeven basis herleidbaar, en door dan de hoogten te vergelijken, kan men uiteindelijk de gegeven veelhoeken qua oppervlakte vergelijken.
Men kan op die manier, tot een rechthoek teruggaande, oppervlakte ook definiëren. En wederom blijkt, zoals in 3.2 bij de rechthoeken, aan de eisen uit 1.6 voldaan te zijn.
| |
3.4
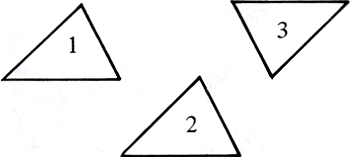
Een aardigheid waaraan ik niet voorbij mag gaan! Uiteindelijk kan men zich beperken tot het afknippen en weer bijplakken van driehoeken en wat het overplaatsen van deze stukken betreft, kan men zich beperken tot translaties en puntspiegelingen.
figuur 5.15
Dus: een driehoek wordt uit een positie 1 in een positie 2 en 3 verplaatst - algemener congruenties hoeven er niet aan te pas te komen.
| |
3.5
Om eerlijk te bekennen: de jubelkreet in 3.3 was prematuur. Los van de eerdere definitie van oppervlakte is het niet evident of knip-plakprocedures ondubbelzinnig tot hetzelfde resultaat leiden. Zou één zelfde veelhoek door middel van twee verschillende knip-plakprocedures niet tot rechthoeken met, zeg: dezelfde basis, maar verschillende hoogten herleid kunnen worden? Of anders gezegd: zou een rechthoek niet door knippen en plakken uiteindelijk in een kleinere overgevoerd kunnen worden?
Het antwoord luidt ontkennend, maar dat dit zo is, is allesbehalve evident en een direct bewijs hiervoor - onafhankelijk van benaderingsprocedures - vereist niet-triviale kunstgrepen. Het is kenmerkend, dat Hilbert's Grundlagen der Geometrie een aantal edities moest doorlopen, alvorens er een
| |
| |
redelijk bewijs voor dit feit in verscheen. Een redelijk bewijs, maar toch zo lastig, dat ik het niet durf reproduceren.
Ziedaar punt nummer drie, waarom oppervlakte een lastpak kan zijn.
| |
4. Oppervlakte en afbeeldingen
De afbeeldingen in en van het vlak waarbij alle afstanden behouden blijven, waarbij het vlak zich als het ware als een vast lichaam gedraagt, heten verplaatsingen of congruenties - verschuivingen, draaiingen, spiegelingen vallen eronder. Dat de verplaatsingen ook de oppervlakte van vlakke figuren ongewijzigd laten, was een eis die we al in 1.9 tegenkwamen.
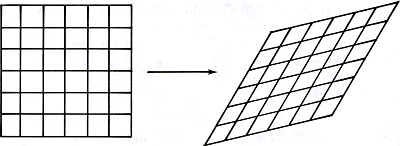
Er bestaan echter meer afbeeldingen die de oppervlakten ongewijzigd laten. Neem bijvoorbeeld de zogenaamde affiniteiten. Deze afbeeldingen laten rechte lijnen rechtlijnig en parallellen parallel - zie figuur 5.16 waar een rooster samen met zijn affien beeld is aangeduid.
figuur 5.16
Bij zo'n affiniteit worden alle oppervlakten met dezelfde factor vermenigvuldigd. Er zijn er waarvoor deze factor juist één is: de zogenaamde speciale affiniteiten.
Dit zijn echter lang niet de enige afbeeldingen die de oppervlakte behouden.
Een soort oppervlaktegetrouwe afbeelding waaraan veel te weinig aandacht wordt geschonken, is het scheren.
Men vatte een vlakke figuur op als gelaagd in evenwijdige lijnstukken, om deze langs elkaar te laten glijden. (In de mechanica noem je zoiets scheren en daaruit neem ik de term over.)
Bij het scheren blijven oppervlakten ongewijzigd. Dit is aanschouwelijk evident. Men schrijft aan de rechtlijnige lagen een dikte toe, dus men denkt zich de figuur uit rechthoekige staafjes opgebouwd, die op elkaar glijden. Voor deze figuur is het behoud van oppervlakte een elementair knip-plakverschijnsel, dat met het steeds maar dunner worden van de lagen wordt meegenomen.

figuur 5.17

figuur 5.18
| |
| |
| |
5. Didactische conclusies
5.1
Bij oppervlakte gaapt er een kloof tussen het aanschouwelijk evidente - het mentale object - en het streng wiskundig beredeneerde begrip. Het is duidelijk dat op school, zelfs op het hoogste niveau, alleen kleine stapjes mogelijk zijn naar mathematische begripsvorming toe. Didactici van de wiskunde, voor wie strenge begripsvorming het doelwit van wiskundeonderwijs is, zullen het onderwerp oppervlakte overslaan of alleen in uiterste verschraling toelaten. Wie het aanschouwelijk tot zijn recht wil laten komen, zal dit onderwerp juist aangrijpen.
Achtjarigen hebben zeker al een welgefundeerd aanschouwelijk idee van oppervlakte. Ze voldoen zonder aarzelen aan de opdracht:
Kleur de helft (een derde) van die figuur rood,
indien de figuur enige regelmatigheid vertoont, zoals een rechthoek, vierkant, cirkel, cirkelsector. Ook leveren zij naar wens gevarieerde oplossingen voor hetzelfde vraagstuk. Bij onregelmatige figuren slagen ze er eveneens in de opgave schattenderwijs op te lossen.
Bij tienjarigen is het benaderend vergelijken en meten van oppervlakten door roosteroverdekkingen, een teken van verdiept inzicht in het onderwerp. De waarnemingen wijzen op een vrij genuanceerd mentaal object oppervlakte. Pas met de formule voor de rechthoek:
lengte maal breedte,
zet de verschraling in het begrijpen van oppervlakte in, die de bovenbouw van de basisschool kenmerkt en waaraan het voortgezet onderwijs zelden of nooit een verlevendigend element toevoegd. Voor zover er dan toch wiskunde van oppervlakte bedreven wordt, is instap, methode en onderwerp vaak vervreemd van de corresponderende mentale objecten, waarmee het fenomeen oppervlakte in het dagelijks leven en in wiskundige toepassingen wordt begrepen.
| |
5.2
Oppervlakte laat zich veelvuldig aangrijpen. Ik som de toegangen resumerend op:
| - | eerlijk verdelen:
| o | door van regelmatigheden te profiteren; |
| o | bij wijze van schatten; |
| o | bij wijze van meten; |
|
| - | vergelijken:
| o | door in elkaar bevat zijn; |
| o | door knip-plakprocedures; |
| o | bij wijze van schatten; |
| o | bij wijze van meten; |
| o | door middel van afbeeldingen; dat wil zeggen: verplaatsingen, affiniteiten, scheringen; |
|
| - | meten:
| o | door uitputten met eenheden;
| - | met telkens verfijnde deeleenheden; |
|
|
| |
| |
|
| o | door benaderingen van binnen en buiten;
| - | met vaste roosters; |
| - | door aangepaste figuren; |
|
| o | door herleiding met knip-plakprocedures; |
| o | door middel van vaste formules; |
| o | door middel van afbeeldingen; dat wil zeggen: verplaatsingen, affiniteiten, scheringen |
|
Uit didactisch oogpunt zijn al deze toegangen aanvaardbaar, de ene met meer, de ander met minder gewicht, en het laat zich niet rechtvaardigen als men zich ter wille van de zuiverheid der methode tot één zou beperken. Integendeel, men zal zoveel mogelijk profiteren van de rijkdom. En dit niettegenstaande de didactische onmogelijkheid van het meer dan lokaal ordenen van dit begrippenveld; dat wil zeggen van:
| - | het stellen van de vraag naar inwendige en uitwendige consistentie van de onderscheiden toegangen; |
| - | het afpalen van bereiken van geldigheid van die toegangen; |
| - | de logische rechtvaardiging van die toegangen in hun onderlinge verband. |
| |
5.3
Dit betekent niet een zich beperken tot een geheel naïeve en onkritische activiteit in een veld, dat immers vol is van voetangels en klemmen. Zodra grootheden in het geding zijn, is er kans op verwarringen: afstanden, tijden, snelheden, meters per seconde en seconden per meter, benzineverbruik per 100 km en afgelegde weg per liter, zijn er voorbeelden van. Voor de constitutie van grootheden als mentale objecten is ook vereist, dat zij met andere geconfronteerd worden. Bij oppervlakte is de omtrek de grote misleider. Op hetzelfde ogenblik dat kinderen er blijk van geven, een oppervlakte eerlijk te kunnen verdelen, laten ze zich toch maar door welgekozen voorbeelden misleiden, oppervlakten van figuren naar hun lineaire afmetingen te beoordelen.

figuur 5.19
Figuur 5.19 toont een situatie, waarin sommigen aan de rechter figuur een grotere oppervlakte toekennen dan aan de linker, wegens de grotere omtrek, terwijl anderen de ‘smalheid’ van de figuur (gemeten als afstand van de schuine parallellen) tot de omgekeerde conclusie verleidt. Dat men de oppervlakte van de Peloponnesos niet kan bepalen door er omheen te zeilen, vond Plato waard om te beklemtonen. Galileï's ‘zak’ aan verschillende kanten dichtgenaaid, om binnen dezelfde oppervlakte verschillende inhouden op te nemen, is een ander historisch voorbeeld dat hier aangehaald mag worden.
Voor de constitutie van het mentaal object oppervlakte zijn ook vereist:
| - | voorbeelden van figuren die hun (misleidende) afwijkingen in lineaire afmetingen ten spijt, dezelfde oppervlakte hebben, zoals de parallellogram-
|
| |
| |
| men met gelijke basis en hoogte; |
| - | voorbeelden van figuren die hun (misleidende) overeenstemming in lineaire afmetingen ten spijt, verschillende oppervlakte hebben, zoals verschillende door buiging uit elkaar ontstaande ruiten (figuur 5.20). |

figuur 5.20
Vooral extreme gevallen zijn instructief:
| - | in figuur 5.19, waar het parallellogram steeds langer en smaller wordt en desniettemin qua oppervlakte hetzelfde blijft; |
| - | in figuur 5.20, waar de ruit tenslotte samenklapt, om geen oppervlakte meer in te sluiten. |
Met een gegeven omtrek willekeurig weinig oppervlakte in te sluiten is - achteraf bekeken - geen kunst. Bij de constitutie van het mentaal object oppervlakte dringt zich als het ware vanzelf het verschijnsel op dat met een gegeven omtrek niet willekeurig veel oppervlakte is in te sluiten. Voor de door een gegeven omtrek in te sluiten oppervlakte is er een bovengrens, die trouwens naar gelang van de tot mededinging opgeroepen figuren kan verschillen.
Dit leidt dan tot de isoperimetrische vraag, onder een soort figuren met dezelfde omtrek die met de grootste oppervlakte te vinden. Dat onder de rechthoeken met gelijke omtrek het vierkant de grootste is, is betrekkelijk gemakkelijk in te zien. Dat onder n-hoeken van gelijke omtrek de regelmatige de grootste is, lijkt vanzelfsprekend, maar is minder gemakkelijk te bewijzen als men van het geval n = 3 afziet. Dat van alle vlakke figuren de cirkel de isoperimetrische eigenschap bezit, lijkt evenzeer evident, maar vereist - om te bewijzen - heel wat wiskunde.
Omtrek en oppervlakte staan enigszins, maar niet geheel los van elkaar; de omtrek legt aan de oppervlakte een bovengrens op. Het analoge een dimensie hoger, in de relatie tussen oppervlakte en inhoud, is wat beide aspecten aangaat, een belangrijke factor van verklaring en beheersing in natuur en techniek. Om uitwisseling van warmte of stof met de buitenwereld te bevorderen scheppen natuur of mens, waar het gewenst is, excessief grote oppervlakten op een kleine ruimte; om deze uitwisseling in andere gevallen tegen te gaan worden vormen aangenomen en geschapen, die zo weinig mogelijk oppervlakte vertonen als met andere gegevens te verenigen valt.
De vraag, die aan de isoperimetrische beantwoordt - een dimensie hoger -: bepaal met een gegeven oppervlakte een zo groot mogelijke inhoud, is mathematisch zelfs nog moeilijker te behandelen dan de isoperimetrische, hoewel het ook hier evident lijkt, dat grote regelmatigheid, in het bijzonder de regelmatigheid van het boloppervlak, een grotere inhoud bij dezelfde oppervlakte garandeert.
| |
| |
| |
Terug- en vooruitblik
Wat een rijkdom van toegangen tot en uitwerkingen van het begrip oppervlakte. Ga na wat er in reken-wiskundemethoden van terechtkomt. Raadpleeg ook Wiskobas-Bulletin, leerplanpublicaties 7 en 9 (handleiding en werkblokken) waaruit dit opstel afkomstig is. Er zijn vragen te over die u uzelf dan zult kunnen stellen.
Even schromelijk als oppervlakte wordt in het vigerende onderwijs verhouding verwaarloosd, het onderwerp van het volgende opstel.
|
|