De mechanisering van het wereldbeeld

[p. 299]

IV. De astronomie in den overgangstijd³⁹

39 Dreyer (2), Zinner (2).

A. Astronomie

59. Bij de behandeling van de lotgevallen van dit vak in den overgangstijd moet men onderscheiden tussen hen die in den trant van Alpetragius en Cusanus speculatieve beschouwingen over den bouw van het wereldstelsel houden en hen die door uitvoering van waarnemingen en berekening van tafels de overeenstemming tussen de heersende theorie en de ervaring op de proef stellen en, waar dit nodig blijkt, verbeteren.

Bij een eerste beschouwing zal het wellicht menigeen toelijken, alsof het grote lijnen trekkende werk van de eerste categorie, dat in den regel in verband staat met algemene metaphysische en natuurphilosophische inzichten en beginselen, zich op een hoger geestelijk niveau beweegt dan de moeizame, door tal van materiële bezwaren bij de vervaardiging en hantering van de vereiste instrumenten belemmerde detailarbeid van de tweede. In werkelijkheid heeft echter de astronomie voor haar vooruitgang in deze periode aan de laatste alles, aan de eerste niets te danken. De niet empirisch controleerbare kosmologische speculatie was een onverantwoord en daardoor onvruchtbaar bedrijf: in de schijnbaar nuchtere waarnemingswerkzaamheid van haar technische beoefenaars handhaafde de astronomie echter den haar van oudsher toekomenden roem, vóór alle andere natuurwetenschappen te hebben beseft, dat werkelijke kennis van de natuur alleen door het systematisch verzamelen van zo exact mogelijk vastgestelde ervaringsfeiten te verkrijgen is en dat de voor het opstellen van verklarende of beschrijvende theorieën onontbeerlijke constructieve phantasie slechts dan niet op dwaalwegen leidt wanneer zij van dit feitenmateriaal uitgaat en de resultaten waartoe zij komt, weer onvoorwaardelijk aan den toets der empirie onderwerpt.

60. Wat de overgangsperiode tussen middeleeuwse en klassieke natuurwetenschap voor nieuws brengt op het gebied der speculatieve kosmologie ligt geheel in de lijn van oppositie tegen het stelsel van Ptolemaios, die door de in Spanje werkende peripatetische philosophen Averroës, Abubacer, Avempace en Alpetragius uit naam van de natuurleer van Aristoteles gevoerd was (II: 141-145). Ook in het oog van verscheidene Christelijke denkers verlenen de excenters en epicykels aan het wereldbeeld een te gekunsteld karakter en zijn de moeilijkheden die de gedachte aan hun physische realisering met zich meebrengt, te groot dan dat ze een hierop gebaseerd wereldstelsel voor een juist beeld van de structuur der werkelijkheid zouden kunnen houden. Een poging om er aan te ontkomen met behulp van een stelsel concentrische spheren doen in de eerste helft van de zestiende eeuw Girolamo Fracastoro en Giovanni Battista Amico en iets later Giovanni Delfino. Geen van drieën hebben ze echter de grondgedachte van hun theorie ver genoeg uitgewerkt om haar voor empirische

[p. 300]

toetsing vatbaar en dus met het stelsel van Ptolemaios vergelijkbaar te maken. Dit laatste blijft het enige, dat er ernstig aanspraak op kan maken, de verschijnselen te redden.

61. Ook het denkbeeld om de dagelijkse hemelbeweging als een afspiegeling van een dagelijkse aswenteling van de aarde op te vatten, duikt in dezen tijd hier en daar op. Zoals we al gezien hebben, was de astronomische mogelijkheid van dit denkbeeld van Ptolemaios af wel algemeen ingezien; de bezwaren die er van oudsher tegen waren aangevoerd, waren steeds van physischen aard geweest en slechts nieuwe physische inzichten konden dan ook een nieuw gezichtspunt in de kwestie openen. Deze worden echter in een in 1525 verschenen werkje van Celio Calcagnini, waarin de aarde als midden in het heelal wentelend om een as en de hemel als rustend wordt aangenomen, niet ontwikkeld. Bovendien is er een omstandigheid, die aan zijn geschrift alle waarde ontneemt: hij acht namelijk de dagelijkse aswenteling van de aarde niet alleen in staat, de dagelijkse hemelbeweging te verklaren, maar hij wil er met behulp van de vage aanvullende hypothese, dat zij nu eens naar deze dan weer naar gene zijde helt, ook de bewegingen van zon, maan en planeten ten opzichte van de vaste sterren en de phasen van de maan uit afleiden.

62. De waarnemende astronomie werd in de vijftiende en zestiende eeuw voornamelijk in Duitsland beoefend. Toen Hendrik van Langenstein, ook bekend als Hendrik van Hessen de Oudere, in 1383 om redenen van politieken aard zijn universitaire loopbaan te Parijs moest beëindigen en, naar zijn vaderland terugkerend, medewerkte om de Universiteit te Weenen te stichten, legde hij daar door zijn eigen astronomisch werk den grondslag voor een traditie van exacte hemelobservatie, die in verscheidene Duitse steden navolging vond. In Weenen zelf leidde ze tot een hoogtepunt der voor-Copernicaanse astronomie in het werk van Peurbach en Regiomontanus, beiden sterrekundigen van grote betekenis, die wellicht de wetenschap nog veel meer bevorderd zouden hebben, wanneer ze niet op zo jeugdigen leeftijd, de eerste op zijn 38e, de tweede op zijn 40e jaar, overleden waren. Wat zij bereikt hebben, bestaat voornamelijk hierin, dat zij door hun uitleggingen het stelsel van Ptolemaios hebben verhelderd en algemeen bekend hebben gemaakt, maar tevens door hun waarnemingen onbetwijfelbaar duidelijk hebben aangetoond, dat het geen voldoende aansluiting aan de ervaring gaf.

Beiden leveren ze tevens een voorbeeld, hoe het humanisme, hoewel als geheel geenszins bevorderlijk voor de ontwikkeling der natuurwetenschap, in sommige van zijn vertegenwoordigers zich toch uitmuntend met een ernstige studie van de natuur liet verenigen. Peurbach gaf aanvankelijk te Weenen colleges in Latijnse poëzie en was vermaard om zijn eigen in het Latijn geschreven gedichten; eerst later kwam hij tot de astronomie en hij bleef hierin als humanist werkzaam, toen de kardinaal Bessarioon, een geboren Griek, die zich beijverde, de antieke wetenschap

[p. 301]

tot nieuw leven te brengen, hem in 1460 uitnodigde, een commentaar op den Almagest samen te stellen. Toen zijn vroege dood in 1461 de voltooiing van dit werk verijdelde, nam Regiomontanus zijn taak over en daarmee werd de band tussen het humanisme en de astronomie nog hechter. Lange jaren heeft hij met den kardinaal in Italië doorgebracht, den Almagest verklarend en intussen handschriften van antieke werken opsporend en ontcijferend. Daarna heeft hij als een pionier van de jonge boekdrukkunst in een eigen drukkerij te Neurenberg naast andere werken van astronomischen aard de Theoricae novae Planetarum van zijn leermeester Peurbach, dat den neerslag van diens colleges te Wenen vormde, in boekvorm algemeen toegankelijk gemaakt en daardoor aan de Griekse astronomie de meest prominente plaats in het Westers wetenschappelijk denken verschaft die zij ooit bezeten had. Tot zover loopt zijn werkzaamheid parallel met die van de vele philosophen en letterkundigen die in de vijftiende en zestiende eeuw Helleense wijsheid en schoonheid in de Westerse cultuur hielpen doordringen. Zij verschilt er echter principieel van, doordat zijn eigen werk als astronoom duidelijk maakte, dat de Griekse wetenschap althans op dit gebied niet kon worden beschouwd als een ideaal voorbeeld, dat tot navolging kon inspireren, maar veeleer als een ontoereikende poging, die tot verbetering aanspoorde.

Het is Regiomontanus niet gegeven geweest, de verbetering, waarvan hij de wenselijkheid zo scherp besefte, tot stand te brengen. Men kan hem op zijn hoogst een zeker voorgevoel toeschrijven van de richting waarin ze gezocht zou moeten worden; hij wijst er namelijk met nadruk op, dat alle planeten zich in hun bewegingen op de een of andere wijze naar de zon richten, de drie buitenplaneten omdat hun voerstraal in den epicykel altijd evenwijdig loopt aan dien van de zon in haar baan om de aarde, de twee binnenplaneten, omdat het middelpunt van hun epicykel altijd op de lijn aarde-zon ligt. Meer dan een voorgevoel van de centrale positie die de zon in het stelsel van Copernicus zou gaan innemen, is dit echter nooit geworden.

Het werk dat Regiomontanus te Neurenberg als waarnemend astronoom verricht had, is na zijn vertrek in 1475, toen hij naar Rome werd ontboden om de kalenderhervorming voor te bereiden, voortgezet door den Neurenbergsen patriciër Bernhard Walther.

B. Gonio- en Trigonometrie⁴⁰

63. Onverbrekelijk met de astronomie verbonden, uit haar behoeften ontstaan en omgekeerd haar bloei bevorderend, was intussen een tak der wiskunde die zowel voor deze zelf als voor haar toepassing in andere natuurwetenschappen van het grootste belang zou blijken te zijn, tot een hogen graad van ontwikkeling gekomen. Het is de uit Indisch-Arabischen

40 Von Braunmühl.

[p. 302]

oorsprong ontsproten en door vertalingen van Arabische geschriften in Europa bekend geworden leer der goniometrische functies en haar toepassing in de vlakke en bolvormige driehoeksmeting.

Van het ogenblik af, dat de behandeling van de bolmeetkunde, die voor de astronomie vereist werd, bij de Grieken uit het zuiver meetkundige stadium waarin ze nog bij Theodosios verkeerde, in dat der berekening was overgegaan, was het noodzakelijk gebleken, inplaats van met hoeken en bogen te rekenen met lijnstukken, die hen bepalen en door hen bepaald worden. De Griekse wiskundigen hadden daarvoor de koorde gekozen, die een cirkelboog onderspant en waren er inderdaad in geslaagd, in hun koordenrekening het verlangde instrument voor de driehoeksmeting te scheppen. Later waren echter de Indische wiskundigen tot het inzicht gekomen, dat de techniek van de berekeningen eenvoudiger wordt, wanneer men daarin een boog zich niet laat vertegenwoordigen door de onderspannende koorde, maar door de helft van de koorde, die zijn tweevoud onderspant. Dit lijnstuk heeft later den Latijnsen naam van sinus verkregen (Fig. 12). De toepassingen die

Fig. 12. De overgang van koordenrekening naar goniometrie. De boog AB wordt in de koordenrekening vertegenwoordigd door de koorde AB, in de goniometrie door BD(sinus) of MD (cosinus). (Tegenwoordig verstaat men onder sinus(cosinus) van bg AB de verhouding van BD (MD) tot den straal van den cirkel, die eertijds de sinus totus heette).

dit nieuwe rekenmiddel in de driehoeksmeting bleek te bezitten, leidden er bovendien toe, bij iederen boog ook de helft van de koorde van het supplement van zijn tweevoud onder den naam cosinus als functie in te voeren.

64. Onafhankelijk van dezen gedachtengang gaven bepaalde waarnemings-instrumenten aanleiding om nog op andere wijzen een hoek door een lijn-stuk te bepalen. Is namelijk (Fig. 13a) AB een verticale staaf (gnomon) van gegeven lengte, waarvan de zon een schaduw BC werpt op een horizontaal plat vlak, dan is de lengte van BC een maat voor de hoogte α van de zon, die de umbra recta of extensa (rechte of gestrekte schaduw) van α heet. Later heeft BC den naam van cotangens van α gekregen, terwijl de hedendaagse wiskunde de verhouding BC/AB zo noemt. Men kan de staaf ook horizontaal opstellen (Fig. 13b) en haar schaduw op een verticaal vlak waar ze loodrecht op staat, meten. De lengte van de schaduw BC heet nu umbra versa (gedraaide schaduw) van de hoogte α, later tangens van α.

Het rekenen met deze vier functies sinus, cosinus, tangens en cotangens is door verscheidene Arabische wiskundigen, waaronder vooral al-

[p. 303]

Battânî, Abu al-Wafâ en Nâsir al-Din al-Tûsî genoemd moeten worden, uitgewerkt en gesystematiseerd tot wat wij nu gonio- en trigonometrie noemen. Met de Arabische wetenschap overgenomen, werd ze in de veertiende en vijftiende eeuw gemeengoed der Westerse astronomen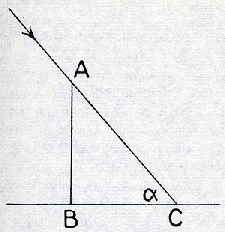

Fig. 13. a) De hoogte α van de zon wordt bepaald door de lengte BC van de schaduw van den gnomon AB op een horizontaal plat vlak. BC heet umbra extensa, later cotangens van α. (Tegenwoordig cot α = BC/AB).

b) De hoogte α van de zon wordt bepaald door de lengte BC van de schaduw van den gnomon AB op een verticaal plat vlak waar AB loodrecht op staat. BC heet umbra versa, later tangens van α. (Tegenwoordig tg α = BC/AB).

zonder nochtans voorlopig de hoogte te bereiken waarop ze bij de Oost-Arabieren had gestaan. Daarop is ze pas weer door Peurbach en vooral door Regiomontanus geheven.

65. De beoefening van de gonio- en trigonometrie is practisch niet mogelijk, wanneer men niet over tafels van de goniometrische functies beschikt. Deze zijn dan ook reeds door Arabische auteurs samengesteld en van hen in West-Europa overgenomen. Aanvankelijk werd daarin met een sexage-simale indeling van den sinus totus gewerkt, d.w.z. men drukte de goniometrische lijnstukken uit in zestigste delen van den straal, in zestigste delen van die zestigste delen enz., juist zoals wij tegenwoordig nog steeds naar het voorbeeld der Babyloniërs met hoeken en bogen doen. Regiomontanus heeft de wiskunde er echter tijdig voor behoed, zich ook in de goniometrie aan deze met de structuur van ons talstelsel strijdige gewoonte te houden. Hij is den sinus totus R (Fig. 12) gaan voorstellen door een macht 10 ⁿ , waarin n varieert van 5 tot 15, wat dus hierop neerkomt, dat hij sinus en tangens ging meten met R/10 ⁿ als eenheid. Zij konden nu met voldoende nauwkeurigheid door gehele getallen worden uitgedrukt,

[p. 304]

waarvan de betekenis echter eerst bepaald was, als men de waarde van n kende. Leest men b.v. in een tafel voor een hoek φ

sin φ = 3432756

en is n = 7, dan beduidt dat in onze tegenwoordige schrijfwijze:

sin φ = 0,3432756.

De waarde van n bepaalt dus het aantal decimalen waarin de functies worden opgegeven.

Het is duidelijk, dat in deze wijze van uitdrukken het denkbeeld van wat in de wandeling decimale breuken heten (eigenlijk positioneel geschreven decimale breuken) ligt opgesloten. Toch zou het nog tot het einde van de zestiende eeuw duren, voordat Simon Stevin het er in opmerkte, een methode aangaf om de waarde van elk cijfer kenbaar te maken zonder vermelding van n, de algemene toepasbaarheid van de nieuwe breuknotatie (die aanvankelijk alleen in de goniometrie was toegepast) aantoonde en de rekentechniek die zij mogelijk maakte, onderwees. Daardoor werd een zeer aanzienlijke vereenvoudiging in het rekenen bereikt, die ook de wiskundige natuurwetenschap zeer ten goede is gekomen.