De mechanisering van het wereldbeeld
(1950)–E.J. Dijksterhuis–
[pagina 272]
| |
A. De school van Jordanus. de invloed van de techniek32. Wij zeiden boven, dat niet steeds scherp is aan te geven, wanneer de periode die we in dit hoofdstuk behandelen, begint. Dat is voor geen enkel vak zo moeilijk te zeggen als voor de mechanica. Wanneer we namelijk voor het enige onderdeel daarvan dat werkelijk reeds als een zelfstandige wetenschap beschouwd kon worden, de statica, de voorgeschiedenis willen overzien, moeten we in Europa teruggaan tot de twaalfde en dertiende eeuw, komen van daar op Arabische, aan Griekse bronnen ontleende geschriften en eindigen dus weer in de Oudheid, bij de afleiding van de hefboomswet in de Aristotelische Quaestiones Mechanicae, bij de axiomatische behandeling van de leer van hefboom en zwaartepunt door Archimedes en bij de theorie der enkelvoudige werktuigen van Heroon. Langs wegen die we niet zullen beschrijven, is al deze kennis, in de Middeleeuwen als Scientia de Ponderibus betiteld (Stevin zou later van Weeghconst spreken), zij het ook in niet geheel ongeschonden gedaante, in West-Europa terecht gekomen, waar ze niet alleen werd opgenomen, maar ook verdere ontwikkeling vond in de school van den nog altijd enigszins vagen dertiende-eeuwsen wiskundige Jordanus Nemorarius. 33. De twee principieel verschillende behandelingswijzen die de fundamentele hefboomswet in de Oudheid had ondervonden, de meer intuïtieve uit de Quaestiones Mechanicae en de streng-axiomatische van Archimedes, blijken nog steeds naast elkaar, soms min of meer met elkaar vervlochten, voort te leven. Echter wordt in de eerste het verband met de grondwet van de peripatetische dynamica losgelaten. De redenering wordt thans gebaseerd op een postulaat, dat men wel het axioma van Jordanus noemt en waarin wordt uitgesproken, dat iets dat in staat is, een zekeren last L over een zekere hoogte h op te heffen, ook het n-voud van dien last over het ne deel van die hoogte kan verplaatsen. Wat dat ‘iets’ is, blijft voorlopig vaag. Eerst veel later zal de klassieke mechanica tot een exacte formulering komen door te zeggen, dat in beide gevallen dezelfde arbeid verricht moet worden of dat beide malen dezelfde hoeveelheid energie moet worden meegedeeld. Met behulp van dit axioma wordt nu in het geschrift Elementa Jordani super demonstrationem ponderis, dat men aan Jordanus zelf pleegt toe te schrijven, de hefboomswet afgeleidGa naar eind23. De gevolgde methode is kennelijk geïnspireerd door die van de Quaestiones Mechanicae maar vermijdt juist de daaraan eigen gebreken. Zij in Fig. 10 een gewichtloze, om O draaibare staaf gegeven, waaraan in A1 en A2 gewichten G1 en G2 hangen, die aan de voorwaarde (1) voldoen. Stel nu, dat het gewicht G2 in A2, dalend naar B2, in staat is, | |
[pagina 273]
| |
G1 van A1 naar B1 te
brengen; men beschouwt nu inplaats van de bogen A1B1 en A2B2 de verticale verplaatsingen B1C1 en B2C2,
die zich verhouden als OB1 en OB2 en waarvoor dus wegens (1) de
voorwaarde 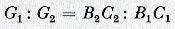 (2) geldt. Zij nu OA3 = OA2 en laat inplaats van een gewicht G1 in A1 een gewicht G2 in A3 hangen, dat bij de aangenomen draaiing naar B3 gaat, en dus een verticale stijging B3C3 ondergaat. Wegens (2) is dus ook 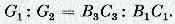 Is dus G2 = n . G1, dan is B3C3 =  en volgens het axioma van Jordanus zal een op de staaf werkend
bewegend vermogen, dat G1 tot B1 kon opheffen, in plaats daarvan G2 naar B3 kunnen brengen. Was nu het gewicht G2 in A2
tot het eerste in staat, dan zou het dus ook G2 van A3 naar B3 kunnen brengen. Maar dat laatste
kan het ten duidelijkste niet doen, omdat de hefboom onder invloed van
gelijke gewichten, die aan weerskanten op gelijke afstanden van O hangen, in evenwicht moet zijn. en volgens het axioma van Jordanus zal een op de staaf werkend
bewegend vermogen, dat G1 tot B1 kon opheffen, in plaats daarvan G2 naar B3 kunnen brengen. Was nu het gewicht G2 in A2
tot het eerste in staat, dan zou het dus ook G2 van A3 naar B3 kunnen brengen. Maar dat laatste
kan het ten duidelijkste niet doen, omdat de hefboom onder invloed van
gelijke gewichten, die aan weerskanten op gelijke afstanden van O hangen, in evenwicht moet zijn.
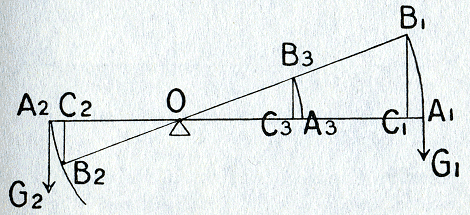 Fig. 10. Afleiding van de hefboomswet in Elementa
Jordani super demonstrationem ponderis.
In deze redenering tekent zich reeds duidelijk het principe der virtuele verplaatsingen of van den virtuelen arbeid af, waarin wordt uitgesproken, dat bij een virtuele (d.w.z. mogelijke) verplaatsing de som van de door de werkende krachten verrichte arbeiden nul is. In het algemeen moeten die verplaatsingen oneindig klein worden genomen; in het onderhavige geval kunnen ze echter eindig zijn; aan deze omstandigheid is het te danken, dat de gehouden redenering slaagt. Volgens de definitieve formulering is de inkleding als bewijs uit het ongerijmde niet nodig; de virtuele verplaatsingen worden niet beschouwd als door de werkende krachten veroorzaakt, maar als zuiver mathematische verplaatsingen van de punten A1 en A2 van de onbezwaarde als lijn gedachte staaf. Voordat dit echter duidelijk was ingezien, heeft de methode steeds weer bloot gestaan aan de o.m. door Simon Stevin (IV: 62) aangevoerde tegenwerping, dat het absurd is, een voorwaarde waaronder krachten elkaar in evenwicht houden, af te leiden uit de onderstelling, dat er beweging optreedt, dus dat de krachten geen evenwicht maken; dat laatste wordt namelijk juist niet ondersteld. 34. Van nog groter belang dan deze afleiding van de hefboomswet is | |
[pagina 274]
| |
een op hetzelfde beginsel berustend bewijs voor de wet van het hellend vlak, omdat daardoor een stelling werd bewezen die steeds buiten het bereik van de Griekse wiskundigen was gebleven. Het komt voor in een geschrift dat in 1565 wel als Jordani Opusculum de Ponderositate gedrukt is, maar dat waarschijnlijk niet van dezelfde hand is als het boven geciteerde werk. Over den auteur, dien men zich in ieder geval tot de school van Jordanus denkt te behoren, tast men in het duister; de betiteling ‘Voorloper van Leonardo’ die Duhem hem placht te geven, is reeds hierom minder gewenst, omdat zij van zijn eigen tijd en herkomst niets zegt. 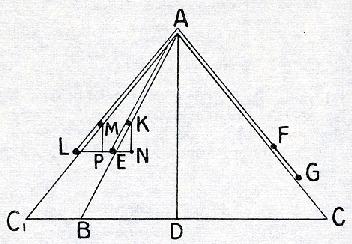 Fig. 11. Afleiding van de wet van het hellend vlak in Jordani Opusculum de Ponderositate.
De schrijver denkt zich (Fig. 11) de hellende vlakken AB en AC met gelijke hoogte AD. Ondersteld wordt AC > AB. Een in Eop AB gelegen lichaam met gewicht G1 is door een over een katrol in A lopend koord met een lichaam van gewicht G2 in F op verbonden. Het gestelde luidt, dat er evenwicht is, als G1: G2 = AB:AC. Is dit niet het geval, dan zal een der gewichten omlaag gaan. Neem aan, dat dit G2 is en dat het van F naar G gaat, daarbij G1 ophijsend tot K. Men denkt zich nu een derde hellend vlak AC1 aangebracht, dat denzelfden hellingshoek heeft als AC, zodat DC1 = DC en hierop in L een gewicht G2. L ligt even hoog als E. Zij LM = EK = FG. Het doel is nu, te bewijzen, dat wanneer G2 in staat is, G1 naar K te brengen, het ook in plaats daarvan G2 van L naar M zou kunnen brengen, wat het wegens de symmetrie natuurlijk juist niet kan doen. Zijn KN en MP de afstanden van K en M boven de horizontale lijn LE, dan gelden de betrekkingen waaruit wegens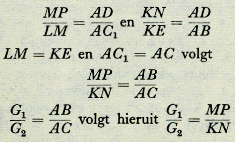 Daar echter ook Is dus G1 = n . G2, dan is KN = 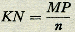 , dus zou G2 op AC inderdaad , dus zou G2 op AC inderdaad | |
[pagina 275]
| |
G2 op AC1 in beweging kunnen brengen, wanneer ondersteld is, dat het G1 kan ophijsen. Het bewijs is hiermee geleverd. De redenering is opmerkelijk wegens het heldere inzicht in het principe der virtuele verplaatsingen; ze is het, naast de andere afleidingen in de werken van de school van Jordanus, tevens als symptoom van het uit de Oudheid reeds bekende streven, de mechanica in wiskundigen trant te behandelen. Er worden algemene axiomata of principes vooropgesteld, die weliswaar niet zo vanzelfsprekend of onbetwijfelbaar aandoen als de axiomata der meetkunde, maar die toch zo aannemelijk zijn, dat men - in overeenstemming met de oorspronkelijke betekenis van axioma: eis, vordering - van den lezer mag verlangen, dat hij ze aanneemt. En verder wordt het probleem als een zuiver mathematisch vraagstuk behandeld. Dat kan natuurlijk alleen, omdat de omstandigheden zich zo gemakkelijk laten idealiseren: gladde vlakken, een buigzaam koord, een katrol zonder wrijving en massa, dat alleen dient om de richting waarin een kracht werkt, te veranderen. Zo verkrijgt de mechanica ook in West-Europa reeds dadelijk de eigenaardige tussenpositie tussen wiskunde en physica, die steeds haar problematiek zal blijven uitmaken: handelend over physische verschijnselen onttrekt zij zich nochtans bij voorbaat door haar ver gaande en gemakkelijk uit te voeren idealisering aan de empirische methoden waar andere delen der physica niet buiten kunnen; zij wordt een aangelegenheid der mathematici en haar resultaten schijnen in de meeste gevallen door de ervaring van het dagelijks leven in het geheel niet bevestigd te worden. Toch is het juist dezelfde dagelijkse ervaring, die haar de problemen stelt en die telkens weer tot haar beoefening prikkelt. 35. Deze mathematische mechanica nu blijkt in de vijftiende en zestiende eeuw hoe langer hoe meer de belangstelling te trekken van de technici die zich met de constructie van machines voor de industrie en van vuurwapenen voor den oorlog, met uitvoering van burgerlijke en militaire bouwwerken of met vervaardiging van instrumenten bezighouden. De diensten die zij hun daarbij bewijst, worden haar veelvoudig vergolden; zij profiteert in hoge mate van de bij haar toepassing opgedane ervaring. Het streven naar een zo voordelig mogelijk gebruik van de beschikbare energie leidt tot nauwkeuriger analyse van de wijze waarop de werktuigen functionneren en tot dusver onbekende verschijnselen stellen haar voor nieuwe problemen. De sterkste impulsen gaan daarbij wel uit van het intensiever wordend gebruik van waterkracht in den mijnbouw en de ijzerindustrie en van de ontwikkeling der vuurwapenen, in het bijzonder van de constructie van steeds grotere kanonnen. Bleef van deze twee toepassingen de eerste nog binnen het sedert de Oudheid traditionele kader van behandeling der mechanische werktuigen, waarin alleen het grensgeval wordt beschouwd, dat macht en last elkaar in evenwicht houden en waarin dus, hoewel het om machines in beweging gaat, het gebied der statica nog niet verlaten wordt, zo leidden het | |
[pagina 276]
| |
gebruik van vuurwapenen en de waarneming van de daarmee te verkrijgen effecten er toe, dat de bewegingsverschijnselen in het middelpunt der belangstelling kwamen te staan en dus het in de Oudheid nog nauwelijks betreden gebied der dynamica ontsloten werd. De gedaante van de kogelbaan en het kennelijk verband tussen de grootte van de ontploffende lading, de elevatie van den vuurmond, het gewicht van het projectiel en de schootsverheid, gaven aanleiding tot onderzoekingen die van het hoogste belang voor de ontwikkeling van de physica geweest zijn. De waargenomen verschijnselen leidden voorts tot een aanzienlijke quantitatieve verruiming van den ervaringskring, doordat er veel grotere snelheden optraden dan in de Oudheid ooit waren voorgekomen. Zo ergens, dan moest hier wel twijfel worden gewekt aan de juistheid van de Aristotelische worptheorie, waarin een projectiel slechts door het medium in beweging wordt gehouden, en tevens de aandacht voor den invloed van den luchtweerstand worden verlevendigd. Behoeften van oeconomischen aard spoorden verder tot theoretisch onderzoek aan: het gebruik van artillerie was uiterst kostbaar en er was dus alle aanleiding om, zoals Biringuccio heeft trachten te doen, te onderzoeken, of men niet door een meer rationele constructie tot een besparing op de kosten van bouw, transport en gebruik kon komen. In de zestiende eeuw gaat verder een belangrijke invloed uit van de constructie van uurwerken en planetaria; de vervaardigers ervan, bekwame mechanici met artistieken aanleg, leerden een nuttig gebruik maken van de beweegkracht van vallende gewichten en gespannen veren en werden gevoerd tot de studie van de verschillende mogelijkheden van bewegings-overdracht. 36. Het getuigt nu wel van de enorme moeilijkheden die aan den opbouw van de mathematische mechanica en daardoor aan het tot stand komen van de klassieke physica in den weg hebben gestaan, dat het nuttig effect van al deze activiteit voor de theoretische beheersing van het vak in de vijftiende en zestiende eeuw toch nog slechts betrekkelijk gering is geweest en dat het tot de zeventiende heeft moeten duren, voordat het gelukt is, de opgedane ervaring ten volle in de wetenschappelijke begripsvorming tot haar recht te doen komen. Het zal na wat we vroeger over de schijnbare aannemelijkheid van de peripatetische dynamica in het licht van de onopzettelijke empirie hebben gezegd, niet moeilijk zijn, dit verschijnsel te begrijpen. De afstand tussen de physische realiteit der bewegingsverschijnselen en de ideële gedachtengangen der theoretische dynamica is zo groot en de resultaten waartoe de laatste voert (b.v. dat een enkele kracht aan een stoffelijk punt een eenparig veranderlijke beweging meedeelt en dat een willekeurig kleine kracht daartoe bij een willekeurig grote massa in staat is) worden door de ervaring, die de eerste (waarin men nooit met stoffelijke punten en alleen werkende krachten te maken heeft) biedt, schijnbaar zo volkomen weersproken, dat het waarlijk | |
[pagina 277]
| |
niet verwonderlijk is, dat men er niet zo gemakkelijk in geslaagd is, hier den weg van de ervaring tot de theoretische behandeling te vinden. Daar komt nog bij, dat juist de drie belangrijkste groepen van bewegingsverschijnselen, val, worp en botsing, zo snel verlopen, dat de niet door instrumentele hulpmiddelen ondersteunde zinlijke waarneming er weinig over leren kan en dat de Aristotelische natuurwetenschap, althans wat de eerste twee van deze fundamentele onderwerpen betreft, de geesten zozeer in dwalingen had verstrikt, dat het weinige dat er nog uit op te maken valt, niet meer onbevangen kon worden opgenomen. Het zou voor het doel van dit boek natuurlijk weinig zin hebben, thans te gaan doen wat een volledige geschiedenis van het natuurwetenschappelijk denken niet zou mogen nalaten, namelijk voor de verschillende auteurs van de overgangsperiode vaststellen, in hoeverre zij over de verschijnselen die de mechanica behandelt, nog zuiver Aristotelisch denken, in hoeverre zich reeds een stemming van radicalen twijfel en principieel verzet begint te openbaren en in welke opzichten zij er reeds in slagen, nieuwe wegen te vinden of althans nieuwe perspectieven te openen. Wij beperken ons er weer toe, enkele karakteristieke punten in het licht te stellen. We spreken daartoe eerst over het aandeel in de ontwikkeling der mechanica van een der belangwekkendste figuren uit het tijdvak dat ons bezighoudt, den Italiaansen kunstenaar Leonardo da Vinci. Door zijn levensomstandigheden evenzeer vrijstaand ten opzichte van de officiële wetenschap der Universiteiten als onafhankelijk van de tradities van het humanistengilde, vurig belangstellend in alles wat de natuur betreft en technisch uitzonderlijk begaafd, lijkt hij wel de eerste, bij wien men een zelfstandige, oorspronkelijke en door alle beschikbare bronnen gevoede visie op de natuurverschijnselen mag verwachten. Zo ergens, dan moet zich hier de komende vernieuwing aankondigen. | |
B. Leonardo da VinciGa naar eind2437. Het is niet gemakkelijk, zich een enigszins duidelijke voorstelling te vormen van den inhoud en de betekenis van Leonardo's natuurwetenschappelijk denken. De aantekenboekjes, waarin hij gewend was, alle opmerkingen te noteren waartoe lectuur van geschriften van anderen of eigen overwegingen aanleiding gaven, bevatten weliswaar talloze passages over physische en technische onderwerpen, maar deze hangen onderling vaak zo weinig samen, zijn zo fragmentarisch van aard en bieden niet zelden zo grote moeilijkheden van interpretatie, dat uit de bestudering niet licht een scherp beeld van zijn wetenschappelijke persoonlijkheid oprijst. Aanvankelijk voelt men zich deels verward door de veelheid der aangeroerde problemen en door het telkens afbreken van het betoog, deels overweldigd door den rijkdom der ontwikkelde gedachten, de leven- | |
[pagina 278]
| |
digheid en het beeldend karakter van den stijl en den onmiskenbaren adem van genialiteit, die alles doordringt. Is men bij voortgezette lectuur deze twee oorzaken van vertroebeling van den kritischen zin te boven gekomen, dan blijkt het nog steeds moeilijk te zijn, tot een juist oordeel over de wetenschappelijke en historische waarde van het gelezene te komen: het is vaak niet mogelijk om door de vaagheid van de soms tot lyrische bewogenheid stijgende uitdrukkingswijze heen tot de gedachte van den schrijver door te dringen; telkens weer blijft men in het onzekere verkeren over de betekenis die hij aan verschillende veel gebruikte termen hecht en men slaagt er vaak niet in, het logisch verband tussen de aan eenzelfde onderwerp gewijde beschouwingen op te sporen. Wanneer men echter tenslotte, na zich zo goed mogelijk te hebben onttrokken aan den suggestieven invloed van de vele aan Leonardo als beoefenaar der natuurwetenschap gewijde studies, waarin zijn prestaties op dit gebied panegyrisch worden verheerlijktGa naar eind25, de nuchtere vraag stelt, wat nu eigenlijk het resultaat is van deze bladzijdenlange ontboezemingen, beschouwingen en problemen, welke positieve bijdrage tot de ontwikkeling der natuurwetenschap er in geleverd wordt, dan kan men moeilijk tot een andere conclusie komen, dan dat deze in aantal en betekenis geringer zijn dan men op grond van de reputatie die hij allerwege geniet, zou mogen verwachten. 38. Aard en inhoud van zijn aantekeningen maken het verder ook moeilijk, de juistheid toe te geven van de gangbare bewering, dat, zij, wanneer zij maar tijdig bekend waren geworden, de geboorte der klassieke natuurwetenschap een of anderhalve eeuw zouden hebben kunnen vervroegen. Het is nauwelijks aannemelijk te achten, dat deze chaotische verzameling van notities, waarin flitsen van genialiteit afgewisseld worden door heel gewone excerpten uit alom bekende werken, in handen van anderen aan het algemene peil der wetenschapsbeoefening meer ten goede zouden zijn gekomen dan nu de auteur ze zijn gehele leven onder zijn berusting heeft gehouden en zij eerst na zijn dood langs verschillende kanalen toch nog bekend zijn geworden. Of wordt bedoeld, dat zij die vervroeging zouden hebben kunnen bewerken, wanneer Leonardo zich er toe gezet had, zijn gedachten systematisch te ordenen en in boekvorm wereldkundig te maken? Dan gaat men uit van de onderstelling, dat hij voor zich zelf tot een voldoend helder en omvattend natuurwetenschappelijk inzicht had kunnen komen of wellich gekomen is om de nodige afronding en systematisering werkelijk te kunnen uitvoeren; die onderstelling wordt echter juist door het chaotisch karakter der aantekeningen, door de vele tegenstrijdigheden die er in voorkomen, door de vaagheid der gebruikte terminologie, door het ontbreken van ieder spoor van logischen opbouw, wel zeer onwaarschijnlijk gemaakt. Daarom kan men ook, zoals wel geschiedtGa naar eind26, kritiek op wat in de aantekenboekjes staat, niet afwijzen op grond van de overweging, dat zij een verzameling schetsen en notities bevatten, die hun | |
[pagina 279]
| |
logischen samenhang eerst bij de verwerking tot een boek verkregen zouden hebben. Ongetwijfeld is een boek meer dan de verzameling van de aantekeningen en ontwerpen waaruit het gegroeid is, maar is het aannemelijk, dat het inzichten zou bevatten waarvan in die aantekeningen en ontwerpen niets te bespeuren valt? Het is ook niet juist, te beweren, dat Leonardo zijn notities slechts voor persoonlijk gebruik maakte: wanneer hij op 22 Maart 1508 te Florence het manuscript begint dat tegenwoordig als het Arundel ms 263 in het British Museum berust, spreekt hij al dadelijk den lezer toeGa naar eind27 en men ontmoet te vaak verschillende redacties van eenzelfde gedachte om hierin geen concepten voor een publicatie te zien. Zijn vriend, de wiskundige Luca Pacioli, vermeldt een werk over locale beweging, stoot en gewicht en alle andere krachten, dat hij trachtte te voltooienGa naar eind28. Het heeft ongetwijfeld symptomatische betekenis voor de structuur van zijn wetenschappelijk denken, dat zulke publicaties nooit klaar zijn gekomen. 39. Wij zijn ons natuurlijk ten volle bewust van de disharmonie tussen deze wijze om over Leonardo als beoefenaar der natuurwetenschap te schrijven en de gangbare beoordeling van de verdiensten die hij als zodanig bezit. Voorzover dat gemis aan overeenstemming berust op interpretatieverschillen die vatbaar zijn voor een redelijke discussie, zullen we er beneden op terugkomen. Er zijn echter ook beschouwingen over hem in omloop, die iemand slechts tot de zijne zou kunnen maken, wanneer hij de auteurs evenaarde in het bezit van bijzondere vermogens om historische samenhangen te zien. Hij zou dan b.v. in staat moeten zijn, om in Leonardo's uitlating: ‘Ieder gewicht streeft er naar langs den kortsten weg naar het centrum te vallen’ de kern van Newton's gravitatieleer te herkennen en in de aantekening: ‘Schrijf over de natuur van den tijd onafhankelijk van zijn geometrie’ een aanwijzing te ontdekken van den weg die later door Einstein betreden zou wordenGa naar eind29. Leonardo lijkt ons op natuurwetenschappelijk gebied eerder de rusteloze zoeker dan de heldere geest, die anderen wegen wijst. Dat maakt hem echter voor het doel van dit werk zo bij uitstek geschikt. Men kan niet duidelijker beseffen, hoe moeilijk het geweest is, den weg uit de peripatetische naar de klassieke natuurwetenschap te vinden dan wanneer men iemand met zijn genialiteit, werkkracht, belangstelling en hoge technische begaafdheid ziet worstelen met de essentiële duisterheden die de grondslagen der mechanica omhullen. 40. Nu loopt men natuurlijk, als men hem zo beschouwt, altijd gevaar, dat men te veel let op de moeilijkheden die hij niet te boven is gekomen en te weinig aandacht overhoudt voor de gevallen waarin hij de wetenschap zelf wel vooruit heeft gebracht of haar beoefening heeft bevorderd. Om dat gevaar te ontgaan, wijzen we eerst op de aanzienlijke plaats die de mechanische technologie steeds in zijn leven heeft ingenomen. Hoewel hij thans voor alles als schilder bekend staat, is hij feitelijk nog meer | |
[pagina 280]
| |
ingenieur geweest dan beeldend kunstenaar en dat zowel op burgerlijk als op militair gebied. Wanneer hij in 1483 zijn diensten aanbiedt aan den hertog van Milaan, Ludovico Sforza, en daartoe in een brief een overzicht geeft van de prestaties waartoe hij zich in staat acht, handelen van de tien punten waaronder hij deze samenvat, er negen over oorlogsaangelegenhedenGa naar eind30. Er zijn perioden in zijn leven waarin hij de kunst geheel verwaarloost ter wille van waterbouwkundige werkzaamheden en constructie van machines. Zijn aantekeningen bevatten talloze schetsen van werktuigen, waaronder vooral de projecten van vliegtuigen de aandacht trekken. Ter voorbereiding hierop heeft hij een uitvoerige studie van het vliegen van vogels gemaakt, die daartoe geheel uit een oogpunt van mechanica worden beschouwdGa naar eind31. Het is duidelijk, hoezeer door al dergelijke werkzaamheden waarin hij bovendien niet alleen stond, maar aanknoopte bij een technologische traditie die op haar beurt gevoed werd door de antieke technische overlevering, de kring der natuurwetenschappelijke belangstelling moest worden uitgebreid buiten de voornamelijk door philosophische gezichtspunten bepaalde grenzen, waarbinnen zij zich in de Scholastiek opgesloten had gezien. Die grenzen waren deels zeer eng, deels zeer ruim geweest; ruim in zoverre als het denken er naar gestreefd had, den gehelen kosmos van zijn diepste gronden tot aan zijn uiterste voleindiging te omvatten, eng doordat men in het licht van een zo verheven doelstelling blind was gebleven voor de betekenis van menig alledaags natuurverschijnsel en voor de behoeften van de praktijk der samenleving. Thans was de natuurwetenschap echter op weg om in te halen wat Oudheid en Middeleeuwen gezamenlijk hadden verzuimd; ze begon langzamerhand te beseffen wat de techniek voor haar en zij voor de techniek kon betekenen. 41. Sprekende over de positieve bijdragen die Leonardo tot de ontwikkeling der natuurwetenschap geleverd heeft, moeten we in de tweede plaats zijn onderzoekingen op het gebied der statica vermelden. Zijn aantekeningen hierover bevatten weliswaar voor een deel niet meer dan excerpten uit de werken van Jordanus Nemorarius en zijn school, maar leveren anderzijds het bewijs, dat hij de daaraan ontleende theorieën heeft uitgebreid en op nieuwe problemen heeft toegepast. Zo laat hij zien, hoe men door toepassing van de hefboomswet de spanningen kan vinden in de twee delen van een aan twee ophangpunten bevestigd koord dat in een willekeurig punt met een gewicht bezwaard is; hij geeft een afleiding voor het zwaartepunt van een viervlak en een benaderde bepaling voor dat van een cirkelsector; hij schetst een uiterst aanschouwelijke proefondervindelijke controle van de wet van het hellend vlak en lost verscheidene vraagstukken over enkelvoudige en samengestelde werktuigen op. Opmerkelijk is bij dit alles echter de onverschilligheid voor den logischen samenhang der verschillende begrippen en stellingen, voor den opbouw van een theoretisch systeem. Al de zorg die hieraan door Archi- | |
[pagina 281]
| |
medes en zijn Arabische commentatoren en in de school van Jordanus besteed was, schijnt hem geen belang in te boezemen; het is alsof het hem alleen te doen is om de regels waardoor hij concrete vraagstukken kan oplossen, of hij alles meer als technicus dan als theoretisch natuuronderzoeker en als mathematicus ziet. Men moet daarbij echter steeds in den technicus den beeldenden kunstenaar begrepen denken, zoals in zijn werkzaamheid als schilder en beeldhouwer ook altijd de ingenieur mede in actie is. Er bestaat voor hem niet slechts een schoonheid die het aesthetisch schouwend oog verrukt, maar ook een die den technischen zin, het gevoel voor vernuftige doelmatigheid, bevredigt. Zijn uitvoerige anatomische studiën hebben niet alleen ten doel, het menselijk lichaam in rust of beweging natuurgetrouw af te beelden zoals het oog het ziet, maar ook, het als mechanisch werktuig zo goed te leren verstaan, dat de afbeelding ook technisch correct is. Zijn belangstelling in theoretische en experimentele zwaartepuntsbepalingen, hoewel in de allereerste plaats bepaald door zijn onvermoeibare pogingen, een vliegtuig te construeren, wordt mede gevoed door zijn streven naar een technisch verantwoorde schilderkunst. 42. Dat wij in Leonardo zoveel meer den op de practische toepasbaarheid van het weten ingestelden technicus dan den naar redelijke fundering en logische ordening strevenden theoreticus zien, kan wellicht in strijd lijken met den uitbundigen lof dien hij in sommige van zijn aphorismen aan de wiskunde als onmisbaren grondslag voor de mechanica toezwaait. Als een tweede Plato verklaart hij, dat wie geen wiskundige is, hem niet lezen moetGa naar eind32. Wij hebben hier echter iets dergelijks als we bij Roger Bacon ontmoeten: het is iets anders, of men in abstracto de wiskunde als grondslag der natuurwetenschap hooghoudt, dan dat men in concreto weet, welk voordeel men op een bepaald gebied uit haar gebruik trekken kan. Evengoed als voor den theoretischen opbouw kan zij immers voor de practische toepassing dienen en wellicht heeft Leonardo voor alles aan dit laatste gedacht. In dezen zin zou dan ook zijn uitspraak: ‘De mechanica is het paradijs der mathematische wetenschappen, want door haar komt men tot de mathematische vrucht’Ga naar eind33 moeten worden verstaan. Het trekt overigens de aandacht, dat wiskundige redeneringen in de aantekeningen van Leonardo een slechts onbelangrijke plaats innemen. De lezer die, aan den hem gestelden eis denkend, de lectuur begint, voelt onder de stromen van woorden waarin de meester zijn gedachten meer verbergt dan dat hij ze er door uitdrukt, telkens weer het verlangen opkomen naar eens een enkel mathematisch betoog, een enkel exact functioneel verband. En voorzover wiskundige methoden practisch worden toegepast, krijgt men niet den indruk van grote bedrevenheid. 43. Wanneer we nu in de mechanica overgaan tot het gebied der elementaire dynamica, het terrein waarop zich de overgang van antieke naar klassieke natuurwetenschap voornamelijk zou voltrekken, vinden we | |
[pagina 282]
| |
Leonardo volop gewikkeld in de worstelingen om inzicht die zijn figuur voor ons zo belangwekkend maken. Twee groepen aantekeningen vragen daarbij vooral onze aandacht, die over het begrip forza en die over de wetten van den vrijen valGa naar eind34. In die van de eerste groep wordt forza in herhaalde beschouwingen, die opvallen door een mystiek en hymnisch karakter, omschreven als Een spiritueel vermogen, een onzichtbare onstoffelijke macht, die door middel van een accidentelen uitwendigen dwang door beweging wordt voortgebracht en ingestort in lichamen, die uit hun natuurlijke zijnswijze en rust zijn gebracht; zij geeft aan die lichamen een actief leven, een wonderbaarlijke kracht, dwingt alle geschapen dingen van vorm en plaats te veranderen, snelt met razernij haar dood tegemoet en neemt verschillende vormen aan al naar gelang de oorzaken zijn. Langzaamheid maakt haar sterk en snelheid zwak; zij wordt geboren door dwang en sterft door vrijheid. Hoe groter zij is, des te sneller verteert zij zich. Zij verjaagt met geweld alles, wat zich tegen haar vernietiging verzet; zij streeft er naar, haar oorzaak, die zich tegen haar verzet, te overwinnen en te doden en gaat in die overwinning zelf te gronde. Zij wordt des te krachtiger naarmate zij groteren tegenstand ondervindt. Ieder ding ontvlucht gaarne zijn dood. Onder dwang gebracht oefent ieder ding dwang uit. Geen ding beweegt zich zonder haar. Het lichaam waar in ze ontstaat, groeit noch in gewicht noch in vorm. Geen beweging die door haar wordt teweeggebracht is duurzaam. Zij groeit in de inspanning en verdwijnt door rust. Het lichaam waarin ze gebracht is, is van zijn vrijheid beroofd. Vaak brengt zij door middel van beweging nieuwe forza voort. De auteurs over Leonardo plegen deze passage te citeren als een kenmerkend voorbeeld niet alleen van zijn geïnspireerden stijl, maar ook van zijn belangrijkheid voor de ontwikkeling der natuurwetenschap. Zij laten dan echter in den regel na, haar ook uit te leggen en duidelijk te maken, in hoeverre het wetenschappelijk denken nu eigenlijk door ontboezemingen als deze wordt verhelderd en verrijkt. Enkelen geven wel een interpretatie; zo meent Duhem, dat Leonardo blijkbaar den gedachtengang van de Parijse Terministen volgt en dat zijn forza hetzelfde is als wat zij impetus noemen. Het is echter moeilijk te zien, hoe deze opvatting met den boven weergegeven tekst te rijmen is. Bij lichamen, die door dwang uit hun natuurlijke zijnswijze gebracht zijn, denkt men onwillekeurig aan een omhoog getild zwaar lichaam of aan een gespannen boog of veer. Dat de forza, die er door deze beweging aan meegedeeld is, naar haar eigen vernietiging streeft, kan betekenen, dat de steen terug tracht te vallen naar zijn natuurlijke plaats en dat de boog zich wil ontspannen. De forza moet zich daarbij verteren, maar de impetus neemt juist toe. Eerder dan aan impetus, dus aan iets, dat een zekere verwantschap met kinetische energie vertoont, voelt men zich geneigd aan de potentiële energie te denken die de genoemde lichamen door gedwongen verplaatsing uit hun natuurlijke rust gekregen hebben. Het blijft dan echter weer | |
[pagina 283]
| |
duister, wat het betekent, dat de forza krachtiger wordt, naarmate zij meer tegenstand ondervindt en zich des te sneller verteert, naarmate zij groter is. Ook geldt voor haar niet, dat ieder ding gaarne zijn dood ontvlucht en dat niets zich zonder haar beweegt; dit laatste doet weer meer aan impetus denken, terwijl de elders herhaalde mededeling, dat langzaamheid haar sterk maakt en snelheid zwak, onweerstaanbaar de gedachte wekt aan den z.g. Gulden Regel der Mechanica, die uitspreekt, dat men bij gebruik van een toestel aan kracht wint wat men aan weg verliest; een macht, die veel kleiner is dan de last, moet in denzelfden tijd over een veel groteren weg, dus sneller werken. Wij zullen ons echter niet verder verdiepen in de vraag, wat men zich bij het woord forza al zo denken kan. De hoofdzaak is, dat dit een vraag blijkt te zijn, dat door de als definitie aangediende beschouwing over forza niet duidelijk wordt gemaakt, wat men zich bij dit woord denken moet, dat den lezer een raadsel ter oplossing wordt gegeven, maar geen inlichtingen ter verheldering van zijn denken verstrekt worden. Van een uiteenzetting waarvan het historisch belang voor de ontwikkeling der natuurwetenschap geroemd wordt, verwacht men echter juist dit laatste. 44. Toch is de passage historisch belangrijk, namelijk als bijdrage, niet tot den groei der mechanica, maar tot ons inzicht in de moeilijkheden die aan dien groei in den weg stonden. Leonardo streeft er blijkbaar naar, een begrip op te stellen, dat een exacten vorm zou kunnen geven aan de vage voorstelling die door het woord forza van de omgangstaal gewekt wordt, en die, kunnen we er bijvoegen, nog heden ten dage aan het onwetenschappelijk gebruikte woord kracht verbonden is. Nog steeds worden immers tal van verschillende begrippen die de mechanica reeds lang heeft leren onderscheiden, door het ene woord kracht weergegeven. Men spreekt van de kracht, waarmee iets gedrukt of getrokken wordt, maar ook van de kracht, waarmee een lichaam tegen een ander botst of waarmee het zijn beweging tracht voort te zetten, van de spankracht van een gas, van de kracht van stromend of door stuwing tot rust gebracht water, van de levende kracht van een bewegend lichaam, van de kracht van een werkende, maar ook die van een rustende machine en in meer dan een zin van electrische en magnetische kracht. De klassieke natuurwetenschap heeft reeds lang geleerd, dat men, exact sprekend, slechts in enkele van al deze gevallen werkelijk het woord kracht gebruiken mag; ze heeft voor de andere telkens een der termen traagheid, impuls, druk, vermogen, energie, lading, poolsterkte, veldsterkte ter beschikking gesteld en daardoor de begripsverwarring leren vermijden die de in de taal voortlevende veelzinnigheid van den term kracht steeds weer dreigt te bewerken. Dat is het resultaat geweest van een eeuwenlange ontwikkeling, waarop wij thans terugzien, maar die ten tijde van Leonardo nog moest beginnen. De geciteerde passage is naast andere, waarin hij de termen peso, percussione, potenza, gravità omschrijft of zonder omschrijving gebruikt, | |
[pagina 284]
| |
een bewijs, hoezeer Leonardo op dit gebied om klaarheid geworsteld heeft. Dat hij die klaarheid niet bereikt heeft, dat wij dus moeten trachten op te sporen, wat hij zich bij de technische termen der mechanica gedacht kan hebben, in plaats van dat hij het ons vertelt, mag ons niet verhinderen, zijn poging naar waarde te schatten. In ieder geval klinkt in zijn beschouwingen een nieuw geluid, dat van den onafhankelijken, door de tradities der officiële wetenschap niet ondersteunden, maar evenmin belemmerden, op eigen inzicht vertrouwenden denker. 45. Een tweede voorbeeld van een strijd met de wezenlijke begripsmoeilijkheden der mechanica vinden we in de tweede der boven onderscheiden groepen van aantekeningen over dynamische onderwerpen, waarin hij zich uitspreekt over het verband van tijd, snelheid en afgelegden weg in den vrijen val. Verscheidene auteurs menen in die aantekeningen te kunnen lezen, dat hij een evenredigheid tussen snelheid en tijd zou hebben aangenomen en dat hij op dat punt dus reeds tot het inzicht zou zijn gekomen dat door de klassieke mechanica bevestigd zou worden. Wij zullen in het volgende, zonder in details te treden, uiteenzetten, waarom deze mening ons onjuist voorkomt en op welke gronden wij in zijn woorden de bewering lezen, dat bij vrijen val uit rust de in opvolgende gelijke tijdvakken afgelegde wegen zich verhouden als de opvolgende natuurlijke getallen. De oorzaak, dat eenzelfde groep aantekeningen op twee zo volkomen verschillende wijzen geïnterpreteerd kan worden, ligt weer daarin, dat het zo moeilijk is vast te stellen, wat Leonardo eigenlijk met de algemeen gebruikelijke termen der bewegingsleer bedoelt. Dezelfde onzekerheid, die boven bij het gebruik van het woord forza bleek te bestaan, doet zich nu voor bij de termen moto en velocità. Er is telkens sprake van un grado di moto, een graad beweging. Deze vertaling beduidt echter op zich zelf niets; men moet dus, wil men het betoog in begrijpelijken vorm weergeven, al dadelijk gaan interpreteren. Doet men dat door met Duhem moto te identificeren met het latere begrip impuls of hoeveelheid beweging (quantitas motus), dat het product van massa en snelheid aangeeft, dan kan men uit een aantekening waarin Leonardo zegt, dat een vrij vallend lichaam in iederen graad tijd (grado di tempo) een graad beweging (grado di moto) en een graad snelheid (grado di velocità) verwerft, inderdaad lezen, dat de snelheid in den vrijen val evenredig is met den sedert het begin der beweging verstreken tijd. Men moet daartoe echter nog twee aanvullende onderstellingen maken en wel 1) dat Leonardo met velocità instantane snelheid bedoelt en niet gemiddelde snelheid over een zeker tijdvak, en 2) dat hij, zonder het uit te spreken, als axioma gebruikt, dat een eenmaal verworven snelheid behoudens vernietiging door uitwendige oorzaken behouden blijft. Van de drie onderstellingen, waarop de toekenning van de juiste betrekking tussen snelheid en tijd aan Leonardo berust, wordt echter de | |
[pagina 285]
| |
eerste (dat moto impuls zou betekenen) ondubbelzinnig weersproken door verscheidene teksten die in hetzelfde verband thuishoren als de aantekeningen waarin men de evenredigheid van snelheid en tijd meent te mogen lezen, terwijl de andere twee althans aan ernstigen twijfel onderhevig zijn. Men vindt namelijk telkens moto gebruikt in den zin van afgelegden weg, zodat un grado di moto een bepaalden afstand blijkt aan te duiden. Verder kan velocità ongetwijfeld instantane snelheid betekenen, maar het wordt evengoed gebruikt voor gemiddelde snelheid over zeker tijdvak of over zekeren afstand. En er zijn inderdaad wel passages te vinden, waaruit een inzicht in een vermogen tot volharden in een beweging spreekt, maar geen, waar het beginsel van traagheid in voldoende klaarheid wordt geformuleerd om te mogen aannemen, dat er bij de opstelling van de valwet stilzwijgend een beroep op zou kunnen zijn gedaan. In ieder geval kan men de bewering van Leonardo ook heel anders lezen, namelijk zo, dat wanneer men een aantal van n opvolgende gelijke tijdsdelen (gradi di tempo) Δ t beschouwt en den weg die in het eerste dier tijdvakken door een uit rust vrij vallend lichaam wordt afgelegd, Δ s noemt, de wegen in de daarop volgende tijdvakken opv. 2. Δ s, 3. Δ s enz. bedragen. In iederen grado di tempo komt er dus zulk een afstand (grado di moto) bij. De gemiddelde snelheden over de opvolgende tijdvakken zijn nu: 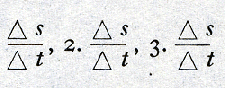 zodat er ook telkens een grado di velocità meer is dan in het voorafgaande. De definitieve formulering, waarmee de reeks aantekeningen over den val besloten wordt, luidt: Een vallend zwaar lichaam verwerft in iederen graad tijd een graad beweging meer dan de verstreken tijdsgraad en ook een graad snelheid meer dan de verstreken bewegingsgraad.Leest men dit zo, dat in het ne tijdvak het aantal afgelegde wegeenheden 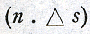 één meer bedraagt dan het rangnummer van het
voorafgegane tijdvak en het aantal snelheidseenheden één meer bedraagt dan het rangnummer van het
voorafgegane tijdvak en het aantal snelheidseenheden 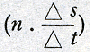 één meer dan het aantal wegeenheden in dat
tijdvak, dan vindt men de boven gegeven interpretatie bevestigd. De
opvatting echter, dat Leonardo een evenredigheid tussen de instantane
snelheid en den sedert het begin der beweging verstreken tijd zou hebben
aangenomen, kan in de aantekening: één meer dan het aantal wegeenheden in dat
tijdvak, dan vindt men de boven gegeven interpretatie bevestigd. De
opvatting echter, dat Leonardo een evenredigheid tussen de instantane
snelheid en den sedert het begin der beweging verstreken tijd zou hebben
aangenomen, kan in de aantekening:
In iedere verdubbelde hoeveelheid tijd verdubbelt het (vallend lichaam) de lengte van de daling en de snelheid der beweging weliswaar een schijnbare bevestiging vinden, als men de woorden ‘de lengte van de daling’ weglaat en ‘snelheid’ als ‘instantane snelheid’ leest, maar zij wordt er onherroepelijk door weerlegd, als men den zin | |
[pagina 286]
| |
onverminkt laat staan en ‘snelheid’ als ‘gemiddelde snelheid’ opvat. De bedoeling is blijkbaar deze: verdubbelt men een van het begin der beweging af gerekend tijdvak, dan zijn in de tweede helft van het aldus verkregen tijdvak de afgelegde weg en de gemiddelde snelheid het dubbele van wat ze in het eerste tijdvak waren. Het is natuurlijk gemakkelijk in te zien, dat een dergelijke betrekking tussen weg en tijd in feite onmogelijk kan bestaan; het gezochte verband mag namelijk niet afhankelijk zijn van de grootte van het gekozen tijdvak Δ t, maar het is dat hier ten duidelijkste wel. Kiest men het namelijk tweemaal zo klein als eerst, dan verhouden zich de wegen, die in de twee helften van het oorspronkelijke tijdvak worden afgelegd, als (1+2):(3+4) dus niet langer als 1:2. Het zou nog meer dan een eeuw duren, voordat Christiaan Huygens op deze wijze de ondenkbaarheid van een ganse klasse van voorgestelde valwetten zou aantonen. Men heeft er zich vaak over verbaasd, dat Leonardo na de opstelling van de wet, die geacht wordt, de evenredigheid van snelheid en tijd uit te spreken, niet ook een poging heeft gedaan om het verband van weg en tijd op te sporen. Die verbazing verdwijnt bij de boven voorgestelde interpretatie vanzelf: de valwet van Leonardo, waarin dus wordt uitgesproken dat de wegen die in opvolgende gelijke tijdsdelen werden afgelegd, zich verhouden als de opvolgende gehele getallen, geeft voor die opvolgende gelijke tijdsdelen tegelijkertijd den weg èn de snelheid aan, maar dit is een gemiddelde snelheid en over de instantane wordt niet gesproken. 46. Wij hebben bij Leonardo's beschouwingen over den vrijen val niet alleen daarom zo lang stilgestaan, omdat het van belang is, zijn gedachtengang zo nauwkeurig mogelijk te benaderen, maar ook en vooral, omdat daarin zo duidelijk een der meest wezenlijke moeilijkheden aan het licht komt die de mechanica te overwinnen heeft gehad, voordat zij de grondslag der wiskundig behandelde physica heeft kunnen worden. Die moeilijkheid bestaat in de noodzaak, voor een grootheid die van den tijd afhangt, een scherpe begripsbepaling te vinden ter fixering van de wijze, waarop ze op een gegeven ogenblik bezig is te veranderen, in casu voor een beweging te zeggen, wat men onder snelheid op zeker ogenblik verstaat. Dat had geen enkele moeilijkheid gegeven, zolang men zich tot eenparige bewegingen had bepaald; men kon hier van de snelheid spreken en deze bepalen als het getal dat aangeeft, welke weg per tijdseenheid wordt afgelegd of ook als quotiënt van den afgelegden weg en den daaraan besteden tijd. Bij een niet-eenparige beweging gaat dat echter niet meer, omdat niet in elke tijdseenheid een even grote afstand wordt afgelegd en het quotiënt van weg en tijd zowel afhangt van de grootte van het beschouwde tijdvak als van het tijdstip waarop het begint. Men kan nu alleen nog maar voor een tijdvak Δ t, dat ten tijde t begint, het quotiënt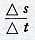 vormen, waarin Δ s den in dat tijdvak
afgelegden weg voorstelt, vormen, waarin Δ s den in dat tijdvak
afgelegden weg voorstelt, | |
[pagina 287]
| |
en dit de gemiddelde snelheid over
dat tijdvak noemen; deze hangt dan echter zowel van t als
van Δ t af. Wanneer men nu echter, t vasthoudend, Δ t tot nul laat
naderen, blijkt voor alle bewegingen die in de mechanica voorkomen, het
differentiequotiënt 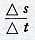 tot een limiet te naderen, die men het
differentiaalquotiënt van s naar t ten tijde t (geschreven ds/dt of de fluxie van s (geschreven ṡ) noemt en deze grootheid wordt nu per
definitie de instantane snelheid ten tijde t genoemd. Zij
geeft dus niet aan, welke weg in de ten tijde t beginnende
tijdseenheid zal worden doorlopen of in de dan eindigende tijdseenheid
doorlopen is, maar ze drukt uit, hoe s ten tijde t bezig is te veranderen. tot een limiet te naderen, die men het
differentiaalquotiënt van s naar t ten tijde t (geschreven ds/dt of de fluxie van s (geschreven ṡ) noemt en deze grootheid wordt nu per
definitie de instantane snelheid ten tijde t genoemd. Zij
geeft dus niet aan, welke weg in de ten tijde t beginnende
tijdseenheid zal worden doorlopen of in de dan eindigende tijdseenheid
doorlopen is, maar ze drukt uit, hoe s ten tijde t bezig is te veranderen.
47. Dezen in onzen tijd reeds lang elementair geworden gedachtengang heeft de mechanica eerst in de zeventiende eeuw ten koste van veel moeite leren volgen en het heeft tot in de negentiende geduurd, voordat de wiskunde er in geslaagd is, er een exacte fundering voor te geven. Daardoor is een verheldering van het denken bereikt, die voor de ontwikkeling van de natuurwetenschap een onschatbare betekenis gehad heeft en die tot de belangrijkste resultaten mag worden gerekend waartoe het wetenschappelijk denken ooit gekomen is. In den tijd waarin Leonardo zijn aantekeningen te boek stelde, was er echter van dit exacte inzicht nog geen sprake: gemiddelde snelheid en instantane snelheid werden niet onderscheiden en verwarringen tussen beide waren aan de orde van den dag. Het is duidelijk, dat het probleem, hoe men een instantane veranderlijkheid door een getal moet karakteriseren, zich niet alleen voordoet bij grootheden die van den tijd afhangen. Wanneer men een grootheid y, die van een onafhankelijk veranderlijke x afhangt, door een kromme in een coördinatenstelsel graphisch voorstelt, leidt de vraag naar de helling van de kromme in een zeker punt tot een volkomen analoog probleem. Men kan die helling namelijk omschrijven als helling van de raaklijn in dat punt en de richting hiervan bepalen als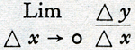 , welke limiet weer als dy/dx
geschreven wordt. Het raaklijnprobleem voor een kromme blijkt mathematisch
identiek te zijn met het snelheidsprobleem voor een beweging. , welke limiet weer als dy/dx
geschreven wordt. Het raaklijnprobleem voor een kromme blijkt mathematisch
identiek te zijn met het snelheidsprobleem voor een beweging.
Het is niet moeilijk in te zien, waarom het zo lang heeft moeten duren, voordat men deze problemen heeft leren oplossen. Er zit iets paradoxaals in, te willen aangeven, hoe een grootheid op zeker tijdstip of in zeker punt bezig is te veranderen, terwijl toch het begrip verandering noodzakelijk vereist, dat er een zeker tijdvak verloopt en het punt zich over een zeker interval verplaatst. Men heeft lang getracht, zich uit deze moeilijkheid te redden door te zeggen, dat men een oneindig klein tijdvak moest beschouwen of de abscis van het punt op de kromme een oneindig | |
[pagina 288]
| |
kleine verandering moest geven, maar slaagde er niet in, te zeggen, wat die woorden betekenen. Eerst de invoering en exacte fundering van het limietbegrip heeft hier klaarheid gebracht en het werken met oneindig kleine grootheden overbodig gemaakt. Dat men daarbij het woord ‘oneindig klein’ is blijven gebruiken (men zegt van een grootheid die tot 0 nadert, d.w.z. die kleiner kan worden gemaakt dan een naar willekeur voorgeschreven positief getal, dat zij oneindig klein wordt) is een uitvloeisel van de wiskundige gewoonte om de begrippen die men scherp heeft leren bepalen, met dezelfde termen te blijven aanduiden die er voor werden gebruikt, toen men er nog slechts een vage voorstelling van had (zo b.v. de termen irrationaal en imaginair in de algebra). Het is een gewoonte die logisch volkomen verantwoord is, maar die bij den buitenstaander altijd weer tot misverstand voert. 48. Het boven behandelde stelt ons nu ook in staat, de eminente practische betekenis te beseffen, die het door Oresme ingevoerde begrip van de graphische voorstelling (II: 125-131) voor de mechanica gehad heeft in den tijd, waarin het begrip differentiaalquotiënt nog slechts in staat van wording verkeerde. In een graphiek van den weg s als functie van den tijd t krijgt namelijk de instantane snelheid ds/dt de meetkundige betekenis van richtingscoëfficiënt van de raaklijn in het punt van de kromme met abscis t. Nu laten zich een raaklijn en haar richting intuïtief duidelijker voorstellen dan de limiet van een quotiënt, waarvan teller en noemer beide tot nul naderen. De graphische voorstelling schiep dus de mogelijkheid, het begrip instantane snelheid meetkundig aanschouwelijk te maken en op grond daarvan kinematische inzichten te verwerven die langs den weg der analyse nog onbereikbaar waren. Dit was vooral van groot belang in een tijd, waarin de algebraïsche symboliek, die voor het tot stand komen van de differentiaalrekening onontbeerlijk was, nog in de kinderschoenen stond. De geleidelijke invoering van wat men de wiskunde der veranderlijkheid kan noemen, in het tijdvak dat met Oresme begint en bij Newton en Leibniz een voorlopige afsluiting zal krijgen, beduidt het inslaan van een richting die onherroepelijk weg voert uit de spheer der antieke wiskunde. Zij vormt een eerste symptoom, dat de leiband der Oudheid, die het mathematisch denken tot nu toe behoed had voor veel gevaren, maar ook voor veel geluk (het geluk namelijk om nieuwe gebieden te ontsluiten) langzamerhand wordt losgelaten. Voor de strenge antieke mathesis, geboren uit den geest der Platonische wijsbegeerte, waarin de ware realiteit het kenmerk der onveranderlijkheid bezit, was een wetenschappelijke behandeling van de veranderlijkheid als zodanig ondenkbaar geweest. Het was een der grote taken waarvoor het denken der Renaissance zich geplaatst zag, om, na zich eerst het wiskundig inzicht der Oudheid eigen te hebben gemaakt, de grenzen die het aan den groei der mathesis gesteld | |
[pagina 289]
| |
had, te overschrijden, en daardoor niet alleen het vak zelf tot een onvermoede hoogte op te voeren, maar het tevens dienstbaar te maken aan de natuurwetenschap. 49. Wij hebben tot dusver voornamelijk gesproken over die gedeelten van Leonardo's aantekeningen over dynamische onderwerpen waarin bij eigen wegen bewandelt. Er zijn echter andere, die, evenals dat met zijn statische onderzoekingen het geval was, meer als schakel in een lange ontwikkelingsketen dan als nieuwe opzet fungeren. Men moet zich namelijk Leonardo wel als een autodidactischen, maar vooral niet als een autochthonen denker voorstellen. Hij heeft veel gelezen: op het gebied der statica kent hij werken van Archimedes en de geschriften uit de school van Jordanus Nemorarius; inzake dynamica is hij vertrouwd met Aristoteles en zijn commentatoren, van wie hij o.m. Albert van Saksen met name citeert. Van al de hierdoor ondergane invloeden geven zijn geschriften overvloedig blijk. Het valt al spoedig op, dat hij onvoorwaardelijk instemt met de betrekking tussen de kracht die een lichaam in beweging brengt en de constante snelheid die het daardoor verkrijgt, waaraan men den naam van grondwet der peripatetische dynamica pleegt te hechten. Wij wezen er reeds eerder op (I: 35), hoe volkomen aannemelijk deze door de nieuwere natuurwetenschap als oerzonde der mechanica ontmaskerde wet aanvankelijk in het licht van de dagelijkse ervaring heeft moeten lijken; het feit, dat een zelfstandige geest als Leonardo, wiens denken niet door een wetenschappelijke opleiding in een vast spoor geleid was, haar zonder een zweem van twijfel of kritiek aanvaardt, bevestigt dat nog eens met alle gewenste duidelijkheid. Meer dan eens schrijft hij haar op, in de volle uitvoerigheid waartoe de geringe ontwikkeling van de wiskunde der functionele afhankelijkheid de physici in dien tijd nog noodzaakte en nog lang zou blijven noodzaken: Als een kracht een lichaam in zekeren tijd over zekeren weg verplaatst, zal dezelfde kracht de helft van dat lichaam in denzelfden tijd over het dubbele van dien weg verplaatsen. Of dezelfde kracht zal de helft van dat lichaam over den gehelen weg in de helft van den tijd verplaatsen. En de helft van de kracht... en zo voort, tot zeven beweringen toe, die men later zou leren samenvatten in een betrekking als: K = c. T.V. waarin K de bewegende kracht, V de snelheid en T een met het gewicht evenredigen weerstand aanduidt, waarmee het lichaam zich verzet tegen pogingen om het in beweging te brengen. 50. Volgt hij in deze dus met de gehele Scholastiek en, kunnen we er reeds dadelijk bijvoegen, alle physici tot in de zeventiende eeuw toe, de oorspronkelijke leer van Aristoteles, zo blijkt hij in de theorie van den worp een aanhanger te zijn van de van het orthodoxe peripatetisme afwijkende impetustheorie der Terministen, die hij echter omvormt in den | |
[pagina 290]
| |
zin van de dynamische beschouwingen, die Cusanus in zijn werk De Ludo Globi (Over het balspel) ontwikkeld had; hij onderscheidt met de eersten in de beweging van een verticaal omhoog of zijdelings weggeworpen projectiel drie phasen, waarvan de eerste uitsluitend door den meegedeelden impetus en de tweede door het conflict van impetus en zwaarte beheerst wordt, maar volgt in de behandeling van de derde phase voor het geval van een over den grond weggeslingerd lichaam de mening van den kardinaal, dat het thans de geometrische vorm van het projectiel is, die de baan bepaaltGa naar eind35. | |
C. De traditie der Parijse mechanicaGa naar eind3651. De klassieke natuurwetenschap zal te zijner tijd geboren worden uit een geest van verzet tegen de als neerdrukkende macht gevoelde autoriteit van Aristoteles. Dat te weten wekt bij de studie van den tijd van haar voorbereiding in de eerste plaats belangstelling voor de lotgevallen van die scholastieke theorieën waarin reeds iets van een kritische gezindheid ten aanzien van zijn natuurwetenschappelijk denken tot uiting was gekomen of waarin denkbeelden waren ontwikkeld die het oorspronkelijke stelsel niet gekend had. Vervolgt men van dit gezichtspunt uit de traditie van de impetustheorie, dan komt men voor verrassingen te staan. In de eerste plaats blijkt het, dat de tijdgenoten der Terministen en de na hen komende generaties hun denkbeelden over de oorzaak van het voortduren van de beweging van een projectum separatum helemaal niet als iets zo revolutionnairs hebben beschouwd als men ze later, het verdere verloop der geschiedenis kennend, in hun qualiteit van symptoom van oppositie tegen Aristoteles onwillekeurig is gaan zien. De impetustheorie heeft haar voorstanders, die er in mondelinge en schriftelijke discussie adhaesie aan betuigen, en haar tegenstanders, die haar onder de te bestrijden meningen opsommen om haar daarna met klem van argumenten te weerleggen, maar dat was nu eenmaal in de Scholastiek de normale gang van zaken: het universiteitsbedrijf leefde van de volledigheid in het registreren en beoordelen van denkbeelden. Zij wordt bekend aan de verschillende in de veertiende eeuw gestichte Duitse universiteiten, waarvan de eerste leiders hun eigen opleiding te Parijs ontvangen hadden en ze beleeft zelfs in het begin van de zestiende eeuw een periode van nieuwen bloei in de plaats van haar herkomst, waarin het voor verscheidene geschriften van haar veertiende-eeuwse grondleggers tot uitgave in boekvorm komt. Van een noemenswaarde verdere ontwikkeling van haar inhoud is daarbij echter geen sprake. Intussen heeft zich dan echter reeds het merkwaardige verschijnsel voorgedaan, en in de zestiende eeuw zal het zich blijven vertonen, dat de officiële wetenschap der universiteiten de theorie, die aanvankelijk zo | |
[pagina 291]
| |
scherp scheen af te wijken van het orthodoxe Aristotelisme, langzamerhand rustig begint te assimileren om haar ten slotte als legitiem bestanddeel der schoolleer te beschouwen. Men zoekt en vindt op verschillende wijzen een compromis of houdt zelfs vol, dat Aristoteles toch eigenlijk ook al had geleerd, dat aan een weggeworpen lichaam een beweegkracht wordt ingeprent. Wanneer men dan bij Scaliger impetus gedefinieerd vindt als een vorm, meegedeeld aan het in beweging gebrachte lichaam, die daarin kan blijven bestaan na verbreking van het contact met den oorspronkelijken motor, klinkt dat al volkomen Aristotelisch. En wanneer aan het eind van de zestiende eeuw de theorie aanvaard wordt door de Spaanse en Portugese Jezuïeten en in gezaghebbende werken als die van Suarez en de Conimbricenses wordt geleerd, blijkt ze volledig in het bezit van de school te zijn overgegaan. 52. Enigszins anders is het met Oresme's leer van de latitudines formarum gelopen. In den oorspronkelijken vorm waarin hij haar had opgesteld en waarin aan de configuratie als zodanig een reële betekenis was gehecht, heeft zij zo goed als geen bekendheid verworven, zoals zijn werken in het algemeen weinig de aandacht schijnen te hebben getrokken. Daarentegen heeft het veertiende-eeuwse geschrift De latitudinibus formarum, waarin met weglating van alle speculatieve elementen een samenvatting wordt gegeven van het zuiver mathematische bestanddeel van Oresme's eigen verhandeling, een zeer grote verspreiding, eerst in handschrift en later in druk, gevonden en de anonyme auteur is als Auctor de latitudinibus bekender geworden dan Oresme zelf. Door de jongste onderzoekingen van A. Maier is intussen de identiteit van dezen Auctor komen vast te staan: het is een Italiaanse Augustijner Eremiet geweest, Jacob van Sint Martinus, ook Jacob van Napels genoemd, die voor het voortbestaan van Oresme's methoden zorg heeft gedragen. In den tijd tussen het verschijnen van zijn verhandeling en de eerste vruchtbare toepassing die het daarin geleerde in handen van Galilei, Beeckman en Descartes zou vinden, heeft de theorie der latitudines niet de minste uitbreiding ondergaan en heeft ze in geen enkel opzicht de natuurwetenschap helpen vooruitbrengen. Dat behoeft ons niet te verwonderen. De leer der graphische voorstelling leent er zich wel toe om als zodanig, dus onafhankelijk van de vraag wat er voorgesteld wordt, theoretisch behandeld te worden, maar vereist daartoe een peil van ontwikkeling der wiskunde dat in de vijftiende en zestiende eeuw nog lang niet bereikt was. En men kan er wel heel veel mee doen voor het aanschouwelijk voorstellen van meetbare functionele afhankelijkheden en voor meetkundige oplossing van vraagstukken die men langs analytischen weg niet of nauwelijks de baas kan, maar dan moet men eerst over zulke afhankelijkheden beschikken en zulke vraagstukken kunnen stellen; echter was de physica daartoe nog lang niet ver genoeg in quantitatief-empirische richting ontwikkeld | |
[pagina 292]
| |
en nog lang niet voldoende mathematisch georiënteerd. Ook moet aan het oplossen van problemen het besef, dat er een probleem bestaat, voorafgaan en de soort van vragen die de nieuwere natuurwetenschap zichzelf voor zou gaan leggen, lag nu eenmaal nog buiten den algemenen wetenschappelijken gezichtskring. Dit alles neemt niet weg, dat Oresme's leer der latitudines in den vorm dien Jacob van Napels er aan gegeven had, wel steeds is blijven voortleven. Aan sommige universiteiten was ze leervak, al maakte ze dan ook geen deel van de examenstof uit. Bovendien blijken echter talloze handschriften en later gedrukte werken, waarvan de inhoud zich daartoe leende, met figuren zoals Oresme ze had leren ontwerpen, geillustreerd te zijn. Meer dan illustraties zijn het echter niet en men kan ze dan ook ontberen; ze begeleiden redeneringen en berekeningen die ook zonder die figuren wel gehouden en gemaakt hadden kunnen worden. Evenals in de dynamica is ook hier het wachten op de geniale handen die de potentieel aanwezige geestelijke rijkdommen tot actueel bestaan zullen voeren. | |
D. De mechanica in de zestiende eeuwGa naar eind3753. Na wat we boven in het algemeen hebben opgemerkt over het voortleven van de denkbeelden der impetustheorie en haar geleidelijke versmelting met de peripatetische natuurphilosophie, is het voor ons doel weer niet nodig, in details na te gaan, welk aandeel zij en welk de orthodox-Aristotelische opvatting (die trouwens zelf in de Scholastiek nog weer onderwerp van talrijke interpretatiediscussies was geweest) bij verschillende auteurs in de verklaring van de fundamentele bewegingsverschijnselen van val en worp gehad heeft. Wij zullen dus slechts enkele algemene opmerkingen over de behandeling van deze verschijnselen in de zestiende eeuw maken; het onderwerp verdient onze aandacht wel; meer toch dan een ander heeft de leer van val en worp het wetenschappelijke milieu bepaald, waarin straks de radicale vernieuwing zal plaats hebben. Voor de leer van de valbeweging is het hierbij niet zozeer van belang te weten, op welke verschillende manieren men al zo getracht heeft, het feit van den val te verklaren en de oorzaak van de aangroeiing van de snelheid op te sporen, als wel te begrijpen, welke principiële moeilijkheden hier aan het doordringen van nieuwere juistere inzichten in den weg stonden. Het zijn er voornamelijk twee geweest, die onderling samenhangen. Vooreerst de schijnbaar zo plausibele, maar in feite zo volkomen onjuist gebleken gedachte, dat aangezien lichamen vallen doordat ze zwaar zijn, zij zeker ook wel des te sneller zullen vallen, naarmate ze zwaarder zijn; en vervolgens de evenzeer voor de hand liggende, maar niettemin uit een | |
[pagina 293]
| |
oogpunt van methode verderfelijke gewoonte, het valverschijnsel altijd te beschouwen in de volle complicatie waarin het zich in de onopzettelijke dagelijkse waarneming van vallende lichamen voordoet en dus den invloed van het medium als een essentieel kenmerk te beschouwen inplaats van er slechts een storenden factor in te zien. Op beide punten lag het denken nog steeds onder den langzamerhand loodzwaar geworden druk van het Aristotelische stelsel van natuurwetenschap, waarin de valsnelheid evenredig was gesteld met het gewicht van het vallend lichaam en omgekeerd evenredig met de dichtheid van het medium en dat niet bij wijze van een geïsoleerde, slechts de physica betreffende empirische wet, die bij gebleken onjuistheid evengoed door een andere vervangen kon worden, maar als een essentieel bestanddeel van een wereldomvattend, in de diepste gronden der wijsbegeerte wortelend natuurbeeld. 54. Wanneer we, vooruitlopend op den gang der ontwikkeling, tegenover deze Aristotelische denkbeelden de zienswijze plaatsen die de natuurwetenschap op den duur als de juiste zou erkennen, zal het ons duidelijk worden, welk een klove die twee scheidt en hoeveel moeite het heeft moeten kosten, haar te overbruggen. De klassieke physica leert, dat men eerst den val van een stoffelijk punt in vacuo moet beschouwen (voor peripatetische opvatting reeds een onmogelijke eis, omdat het vacuum niet bestaat); ze stelt vast, dat de valsnelheid daar (geheel in strijd met de dagelijkse waarneming) onafhankelijk is van het gewicht en verklaart dat door de onderstelling, dat de massa van het stoffelijk punt (een daaraan eigen grootheid die de uitwerking van een er op werkende kracht bepaalt) evenredig is met het gewicht (een raadselachtig verband, dat steeds weer er toe zal verleiden, massa en gewicht te verwarren); vervolgens laat ze zien, dat een op een stoffelijk punt werkende kracht van constante grootte en richting niet, zoals de peripatetische dynamica leerde, een eenparige, maar een eenparig veranderlijke beweging veroorzaakt, hetgeen ze verklaart met behulp van een in het stoffelijk punt zetelend vermogen, in een eenmaal verworven beweging te volharden, een gedachte die lijnrecht in strijd is met het causaliteitsbegrip der Aristotelische wijsbegeerte, dat voor elke beweging een van het mobile te onderscheiden motor eist, maar die daarmee tot op zekere hoogte kan worden verzoend door dat volhardingsvermogen te beschouwen als de uiting van een aan het stoffelijk punt ingeprenten, als inwendigen motor fungerenden impetus. En ten slotte leidt ze langs wiskundigen weg af, dat de in vrijen val uit rust doorlopen weg evenredig is met het quadraat van den sedert het begin der beweging verlopen tijd. Eerst daarna spreekt ze over valbeweging in pleno en vat deze op als het resultaat van de storingen die de in een medium door het lichaam ondervonden opwaartse kracht en de weerstand dien het medium tegen zijn doorklieving biedt, in het ideale valverschijnsel teweegbrengen. | |
[pagina 294]
| |
Echter blijkt het rekening houden met dien weerstand reeds dadelijk tot aanzienlijke mathematische moeilijkheden te voeren. De weerstand blijkt namelijk afhankelijk te zijn van de instantane snelheid, waarvan de grootte echter op ieder ogenblik weer mede wordt bepaald door de weerstanden die het punt op alle voorafgaande ogenblikken heeft ondervonden en die op hun beurt weer bepaald waren door de toen bereikte snelheden, een in zijn algemeenheid onoplosbaar probleem, dat eerst vatbaar wordt voor mathematische behandeling, wanneer men een bepaalde betrekking van afhankelijkheid tussen weerstand en instantane snelheid aanneemt. Wanneer men nu tenslotte nog bedenkt, dat het vallend lichaam tot dusver als stoffelijk punt is beschouwd, zodat men wel weet, wat zijn zwaartepunt doet, maar niet welke bewegingen het zelf nog weer om dat zwaartepunt uitvoert, en dat voor het onderzoek hiervan de kennis van de dynamica van het vaste lichaam vereist wordt, dan wordt ten eerste duidelijk, hoe ontzaglijk gecompliceerd natuurverschijnselen die we dagelijks om ons heen spontaan zien verlopen, in werkelijkheid zijn, vervolgens, dat de natuurwetenschap ons steeds slechts een uiterst vereenvoudigd beeld van die werkelijkheid voor ogen kan voeren, waarin bovendien van allerlei storende omstandigheden is geabstraheerd en tenslotte, hoe machteloos de physica der zestiende eeuw tegenover een dergelijk probleem moest staan en hoezeer de wegen, die zij bewandelde (behandeling in woorden, beschouwing van het verschijnsel in zijn volle complicatie en concrete bepaaldheid, opvatting van storende factoren als essentiële) juist in tegen-overgestelde richting moesten leiden dan waar tenslotte iets van een juist inzicht bereikt zou worden. 55. Daartoe werkte natuurlijk ook een tekort aan empirisch onderzoek mee; slechts de alleroppervlakkigste waarneming van het valverschijnsel - een omlaag dwarrelend blad vergeleken met een vallenden steen - kan den schijn wekken, dat zwaardere lichamen sneller vallen dan lichtere, waarbij nog de onderstelling van een evenredigheid tussen valsnelheid en gewicht geheel uit de lucht gegrepen wordt; dat echter een steen van dubbele grootte denzelfden afstand in tweemaal zo korten tijd zou afleggen, kan nooit iemand hebben geloofd die zijn ogen ook maar even den kost gaf. Het blijkt nu ook, dat deze bewering in den loop der jaren telkens tegengesproken is. In de zesde eeuw had Philoponos haar juistheid al in ronde woorden op grond van proefneming ontkend en uit de zestiende zijn verscheidene gevallen bekend, waarin lang voor Galilei (wien een hardnekkige legende de prioriteit van de ontdekking nog maar steeds blijft toekennen) is geconstateerd, dat de Stagiriet in deze geheel bezijden de waarheid was. Zulk een vaststelling had dan echter helemaal niet de vèrstrekkende consequenties, die ze in het oog van een hedendaagsen physicus had behoren te hebben. Men verovert een vesting niet door een lossen steen in den muur aan te wijzen en zo was er voor het omverwerpen van | |
[pagina 295]
| |
het Aristotelische bolwerk ook heel wat meer nodig dan den Stagiriet op een onjuiste bewering te betrappen. De officiële wetenschap demonstreert dat in deze tijden van beginnenden twijfel aan haar gezag door een merkwaardige onaandoenlijkheid aan den dag te leggen ten aanzien van feiten die met haar stelsel van natuurbeschouwing in strijd bleken te zijn. Dat stelsel leek zo vastgegrond in de natuur der dingen, dat een feit als de ontdekking van Amerika met al de daaraan verbonden, in ons oog verwoestende consequenties voor de geographie, de geophysica, de ethnologie en zelfs de theologie van die dagen, met even grote gelijkmoedigheid werd geaccepteerd en genegeerd als de voor de peripatetische mechanica zo pijnlijke waarneming, dat een loden bol den grond niet eerder bereikt dan een houten, dien men op hetzelfde ogenblik op dezelfde hoogte heeft losgelaten. Niet geïsoleerde feiten zouden het zijn, die de Aristotelische natuurwetenschap ten val brachten, maar een radicale verandering in de methode, waarmee de studie der natuurverschijnselen werd bedreven. 56. Men kan veilig zeggen, dat die verandering zich, wat val en worp betreft, in Galilei voltrekt; aangekondigd wordt ze voor het eerste verschijnsel echter in het werk Diversarum Speculationum mathematicarum et physicarum Liber van den Venetiaansen wiskundige Giovanni Battista Benedetti. De principiële bestrijding die de valwet van Aristoteles in dit boek ondervindt, verwijdert den auteur weliswaar niet zover van den Stagiriet als hij zelf meent - ook Galilei zal nog sterker onder zijn machtigen invloed staan dan hijzelf zou hebben willen toegeven - maar ze bevat toch verscheidene elementen die van een veranderden geest van natuuronderzoek getuigen en doet een eersten stap in de richting van de overwinning der boven aangewezen fundamentele moeilijkheden. Men vindt dezen in de terecht befaamde, maar ten onrechte aan Galilei als oorspronkelijke vondst toegeschreven redenering, waardoor in een gedachtenexperiment bewezen wordt, dat voor lichamen van hetzelfde soortelijk gewicht de valsnelheid in vacuo niet evenredig kan zijn met het gewicht. Benedetti denkt zich daartoe twee congruente lichamen van eenzelfde stof die naast elkaar over een zekeren afstand vallen en die dezen uiteraard in denzelfden tijd doorlopen, door een verbinding van te verwaarlozen gewicht tot één samengevoegd. Het is ondenkbaar, dat daardoor iets aan hun valbeweging zou kunnen veranderen. Echter is er door hun verbinding een lichaam met tweemaal zo groot gewicht ontstaan, dat volgens de physica van Aristoteles den gegeven afstand in de helft van den tijd zou moeten doorlopen. Het alleropmerkelijkste in deze even eenvoudige als vernuftige redenering is wellicht nog het juiste inzicht, dat zij alleen opgaat voor lichamen van dezelfde stof; men kan er bij voorbeeld niet mee aantonen, dat de valtijd over een gegeven afstand in vacuo niet omgekeerd evenredig zou kunnen zijn met het soortelijk gewicht, een onderstelling die Galilei later zal maken. Met het oog op de verdere ontwikkeling van de mechanica is het nog | |
[pagina 296]
| |
van belang op te merken, dat men in Benedetti's werk een duidelijke formulering aantreft van de door Buridan aangegeven verklaring van de versnelling der valbeweging met behulp van de impetustheorie: de impetus (die met de snelheid evenredig wordt gedacht) groeit gestadig aan, omdat de in het lichaam zetelende bewegingsoorzaak voortdurend nieuwen impetus voortbrengt en - aldus de verzwegen praemisse, die de conclusie eerst rechtvaardigt - de eenmaal verkregen impetus behoudens uitwendige oorzaken van vermindering, zoals de luchtweerstand, behouden blijft. Deze gedachtengang vertoont reeds een aanzienlijke mate van overeenstemming met het gronddenkbeeld der klassieke dynamica, dat als resultaat van de werking van een constante kracht een eenparig veranderlijke beweging ontstaat; zij verschilt daarvan alleen in dit opzicht, dat daarin de kracht gedacht wordt als een uitwendige invloed inplaats van als een inwendig bewegend vermogen. Bedenkt men, dat dezelfde verklaring van de versnelde valbeweging in het midden van de zestiende eeuw voorkomt bij Scaliger, wiens denken geheel gevoed wordt door de peripatetische traditie, terwijl ze enkele decennia later aan te treffen zal zijn in geschriften die reeds tot de periode van de klassieke natuurwetenschap kunnen worden gerekend, dan springt de onafgebroken band die de Parijse Terministenschool met de nieuwere physica verbindt, in het oog. Opmerkelijk is nog, dat Benedetti als eerste uitdrukkelijk uitspreekt, dat de impetus die aan een lichaam is ingeprent, het steeds tot een rechtlijnige beweging aandrijft; dat men dus niet, zoals voor hem veelal gedaan was, een impetus voor draaiing van een voor rechtlijnigen voortgang kan onderscheiden. Benedetti noemt het voorbeeld van een aan een touw rondgeslingerden steen; op het ogenblik dat de steen het werptuig verlaat, drijft de ingeprente impetus het tot rechtlijnige beweging langs de raaklijn van den eerst doorlopen cirkel voort en dat de baan niet recht blijft, komt alleen omdat nu ook de zwaarte haar invloed doet gelden. Om deze opmerking verdient hij ook een plaats in de ontwikkelingsgeschiedenis van het traagheidsbeginsel der klassieke mechanica. 57. Het moet Benedetti voorts als grote verdienste worden aangerekend, dat hij, opnieuw als eerste, de volle consequentie trekt van het inzicht in de opwaartse kracht die een lichaam in een vloeistof of een gas ondervindt. Hij baseert er de verwerping op van de Aristotelische onderscheiding van zware en lichte lichamen en keert terug tot de oud-Griekse opvatting, dat alle lichamen zwaar zijn en een lichaam alleen licht lijkt doordat de opwaartse kracht het van zijn gewicht wint. In verband hiermee hecht hij niet de minste waarde aan de Aristotelische argumentatie tegen het vacuum. Hij ziet verder de noodzakelijkheid in, onderscheid te maken tussen de opwaartse kracht die een medium op een daarin geplaatst lichaam uitoefent en den weerstand dien het tegen zijn eigen verdeling door het vallend lichaam biedt, hoewel hij met dezen laatsten invloed nog niet op andere wijze rekening weet te houden dan door het formuleren | |
[pagina 297]
| |
van een voorwaarde, die in verschillende gevallen de gelijkheid ervan moet waarborgen. Hoe zeer hij ondanks zijn vaak heftige kritiek op den Stagiriet nog onder invloed van het Aristotelische denken staat, komt wel heel duidelijk tot uiting, wanneer hij, na het gewicht met de opwaartse kracht verminderd te hebben, de valsnelheid met het verkregen verschil evenredig stelt. 58. Wij wezen boven (III: 35) reeds op de betekenis die de toepassing van artilleristische vuurwapenen in de vijftiende en zestiende eeuw voor de ontwikkeling van de mechanica heeft bezeten, doordat ze de aandacht richtte op den vorm van de kogelbaan en vragen deed rijzen over het verband tussen de grootte van de lading, het gewicht van het projectiel, de elevatie van den vuurmond en de schootsverheid. Over het meest gangbare denkbeeld inzake den baanvorm hebben we bij de bespreking van Leonardo al iets gezegd (III: 50) en toen de onderscheiding van de beweging in drie perioden leren kennen. Men kan deze driedeligheid met alle gewenste duidelijkheid afgebeeld vinden in een figuur van het in 1537 verschenen werk Die geometrische Büxenmeisterey van den Zwitser Walter Hermann RyffGa naar eind38. Men ziet hierin den gewoonlijk aangenomen cirkelvorm van het middelste stuk en de rechtlijnigheid van de beweging in de derde periode, waarin de aanvankelijke impetus geheel verdwenen is en de zwaarte het lichaam nu in natuurlijke valbeweging omlaag voert. De gehele theorie van de driedeligheid vormt een merkwaardig speculatief element in een overigens geheel empirischen tak van wetenschap, een typerend voorbeeld van het goede vertrouwen, waarmee men dergelijke, voor empirische controle toch volkomen onvatbare beweringen op grond van een theorie aanvaardde, misschien ook wel van het toch nog wel heel losse verband tussen wetenschap en practijk, waarin de eerste straffeloos dingen kon beweren die de tweede niet bevestigen kon en deze zich kon veroorloven die beweringen dan ook te negeren. Het is in dit verband tekenend, dat men op het titelblad van hetzelfde werk waarin de driedelige baan zo duidelijk getekend staat, een afbeelding kan aantreffen van een onder geschutvuur liggende belegerde stad, waarop de projectielen doorlopend gekromde banen beschrijven, die men heel goed voor parabolisch zou kunnen houden. De geschetste toepassing van de impetustheorie op den worp had overigens de verdienste, dat zij in haar beschouwingen over de tweede periode, waarin impetus en zwaarte met elkaar strijden, een weg wees om althans iets van het verschijnsel te begrijpen, terwijl alle aan de ervaring ontleende gegevens over het verband der verschillende boven genoemde grootheden noodzakelijk zonder begrip onverwerkt naast elkaar moesten blijven staan. Tartaglia, de Italiaanse wiskundige van de zestiende eeuw, die zulk een belangrijke plaats in de geschiedenis der algebra bekleedt, komt daardoor in zijn Quesiti et Inventioni Diverse (1546) ook al tot de conclusie, dat aangezien die strijd zich doorlopend afspeelt, de gehele baan gekromd | |
[pagina 298]
| |
moet zijn. Vermelding verdient nog de algemeen gedeelde, maar nog volkomen ongegronde overtuiging, dat de maximale schootsverheid op een horizontaal vlak bereikt wordt bij een elevatie van 45°, een resultaat, dat door de latere correcte theorie van de kogelbaan voor den worp in vacuo bevestigd zou worden. |
|

