Clio's stiefkind

[p. 127]

De intrede der wiskunde in de natuurwetenschap

Toen Dijksterhuis in 1932 werd benoemd tot privaatdocent in de geschiedenis van de exacte wetenschappen te Leiden, kwam hij in een omgeving terecht waarin zijn streven om de kloof tussen de natuurwetenschappen en de literaire cultuur te overbruggen met behulp van de wetenschapsgeschiedenis op een positief onthaal kon rekenen. Zijn aantreden in Leiden viel namelijk samen met het begin van een reeks colleges onder de gemeenschappelijke titel ‘Wereldbeeld en wetenschap omstreeks 1700’, waarin van verschillende zijden, zo stond het in de aankondiging, ‘de intrede van de natuurwetenschap als cultuurfactor in de na-middeleeuwse beschaving’ werd belicht. Deze avondcolleges, die voor een ruim publiek waren bestemd, hadden tot doel ‘aan hen die de humaniora beoefenen te doen zien hoe de natuurwetenschap een integraal bestanddeel van onze moderne beschaving geworden is, en aan hen die de natuurwetenschap beoefenen hoezeer die ontwikkeling in aard en richting beïnvloed werd door godsdienstige, filosofische en maatschappelijke stromingen’. Ook Dijksterhuis nam een lezing voor zijn rekening: op 6 december sprak hij over de ‘toepassing van de wiskunde in het natuuronderzoek’. Ruim een jaar later werd de voordracht onder een gewijzigde titel gepubliceerd in De Gids.¹

Het initiatief tot het houden van de lezingen was uitgegaan van twee Leidse hoogleraren, de historicus J. Huizinga en de botanicus L.G.M. Baas Becking. Huizinga mag wel de grote animator van de reeks genoemd worden; hij nam maar liefst vier van de veertien lezingen voor zijn rekening. Maar ook de bijdrage van de tweede initiatiefnemer, Baas Becking, moet niet onderschat worden. Over het algemeen wordt de kloof tussen alfa en bèta vooral als pijnlijk ervaren door de beoefenaars van de natuurwetenschappen en dat geldt ook in dit geval. Huizinga mag misschien op grond van zijn vooraanstaande academische positie de meeste mogelijkheden hebben gehad om het initiatief van de grond te krijgen, uit zijn geschriften blijkt niet dat hij aan de kloof tussen de beide culturen werkelijk geleden heeft. Een dergelijke formulering is meer van toepassing op Baas Becking.

L.G.M. Baas Becking (1895-1963) was in 1930 na een jarenlang verblijf in de Verenigde Staten (hij was verbonden geweest aan Stanford University in Californië) hoogleraar plantkunde in Leiden geworden. Daarvoor was hij al eens een jaar gasthoogleraar in Utrecht geweest en uit die periode (het ging om het academisch jaar 1927-1928) dateert een artikel van zijn hand dat vrij nauwkeurig weergeeft hoe hij dacht over de culturele positie van de natuurwetenschappen. Dat artikel verscheen in 1928 in De Gids onder de op het eerste gezicht wat raadselachtige titel ‘Atheners en Boeotiërs. Een boutade en een apologie’. Bij lezing blijkt het om een aanklacht te gaan tegen de vooral van de kant van de beoefenaars van de humaniora in stand gehouden kloof tussen wat hij noemt ‘twee richtingen van algemene geestelijke vorming, de humanistische en de

1 Aankondigingen onder andere in: Weekblad voor gymnasiaal en middelbaar onderwijs 29 (1932-33) 124-125. In dit blad werd van elke lezing een samenvatting gepubliceerd. Voor de lezing van Dijksterhuis: Ibid., 508-513.

[p. 128]

natuurwetenschappelijke’. De Atheners (de alfa's) beoefenen de geesteswetenschappen, de Boeotiërs (de bèta's) de natuurwetenschappen; de eersten redetwisten op het marktplein over het heil der mensheid, de laatsten slaan de hand aan de ploeg en maken dat geredekavel mogelijk. De Boeotiërs hebben het echter moeilijk om hun activiteiten als volwaardige cultuuruitingen aanvaard te krijgen. Terwijl de dienaren van de natuurwetenschappen alles horen te weten van de filosofie en de literatuur, van Aristoteles tot Zeno en van Ariosto tot Zola, geldt zo'n eis niet omgekeerd voor de beoefenaars van de geesteswetenschappen. De oorzaak daarvan ligt voor een belangrijk deel in de overgrote nadruk die de pleitbezorgers van de natuurwetenschap zelf soms op het nut van hun werk hebben gelegd. Die nadruk op het utiliteitsprincipe verduisterde de onmiskenbaar ethische, esthetische en zelfs religieuze aspecten van de natuurwetenschap, die op grond daarvan tot de cultuur gerekend zou moeten worden. Waar Baas Becking nu voor pleitte was erkenning van de geestelijke en culturele waarde van de natuurwetenschap, want alleen op die manier zou uit een combinatie van oude geesteswetenschap en nieuwe natuurwetenschap een waarlijk moderne, twintigste-eeuwse cultuur kunnen worden opgebouwd.²

Zoiets was Dijksterhuis uit het hart gegrepen; hij had op zijn manier ook al vaak op de heilloze kloof tussen bijvoorbeeld de klassieke en de natuurwetenschappelijke opleiding gewezen. Het mede van Baas Becking uitgegane initiatief voor een collegereeks over de geschiedenis van de vroeg-moderne wetenschap zal daarom zijn hartelijke steun hebben gehad. De veronderstelling is niet al te gewaagd dat de reeks een belangrijke impuls heeft gegeven aan zijn eigen streven om met behulp van de wetenschapsgeschiedenis iets aan die kloof tussen alfa en bèta te doen. Het is altijd goed te weten dat men niet alleen staat.

Alleen al om die reden komt de voordracht over de intrede van de wiskunde in de natuurwetenschap een aparte plaats toe in het werk van Dijksterhuis. Maar ook om inhoudelijke redenen verdient de lezing bijzondere aandacht. Na zijn promotie had Dijksterhuis eerst vooral gepubliceerd over de geschiedenis van de mechanica, het vak waarin hij afgestudeerd was. Val en worp uit 1924 was de belangrijkste publikatie uit die periode. Daarna had hij zich weliswaar intensief beziggehouden met de geschiedenis van de Griekse wiskunde, maar de mechanica bleef in zijn visie op de geschiedenis van de natuurwetenschap de centrale wetenschap, waar uiteindelijk alles om draaide. De grootse uitwerking van die gedachte zou pas na de oorlog komen, in De mechanisering van het wereldbeeld, maar de voordracht over de intrede van de wiskunde in de natuurwetenschap van 1932 was er in zekere zin de eerste voorstudie van. Hier treedt hij voor het eerst buiten het terrein van de wiskunde en de mechanica om te laten zien hoe deze wetenschappen als voortrekker hebben gefungeerd voor de natuurwetenschap als geheel. De voordracht en het artikel markeren dus een belangrijke overgang in het hele oeuvre van Dijksterhuis.

2 L.G.M. Baas Becking, ‘Atheners en Boeotiërs. Een boutade en een apologie’, in: De Gids 92 (1928) iii, 103-113. Ook later heeft Baas Becking zich nog wel zorgelijk uitgelaten over de schromelijke miskenning van de waarde van de natuurwetenschappen in kringen van de beoefenaars van de geesteswetenschappen. In een lezing ‘Biologie en maatschappij’ voor de Vereniging van leraren in de plant- en dierkunde sprak hij op 4 maart 1933 bijvoorbeeld over ‘de meest krasse vervreemding van de natuurwetenschap waaraan een groot deel van de Nederlandse intellectuelen lijden, bijvoorbeeld vele van onze leiders, die over het algemeen uit rechtsgeleerde kringen komen’. Zie het verslag van deze lezing in: Vakblad voor biologen 14 (1932-1933) 151.

[p. 131]

De intrede der wiskunde in de natuurwetenschap

I

In het hier volgende opstel, waarin een der voordrachten die in de cursus 1932-1933 aan de Leidse universiteit onder de algemene titel Wereldbeeld en wetenschap omstreeks 1700 zijn gehouden met enkele vorm wijzigingen wordt weergegeven, wordt getracht de vraag te beantwoorden waar en hoe de wiskunde toepassing heeft kunnen vinden in de natuurwetenschap der zeventiende eeuw en welke invloed daarvan op het wetenschappelijk denken in het algemeen is uitgegaan. Daarbij zullen, met het oog op de impopulariteit der wiskunde buiten de kringen der mathematisch geschoolden^*, op één uitzondering na, alle mathematisch-technische uiteenzettingen worden vermeden, terwijl de bezwaren die uit de grote omvang van het onderwerp voortvloeien, ondervangen zullen worden door beperking tot de grote lijnen en de principiële gezichtspunten.

Om die grote lijnen reeds dadelijk vast te leggen knopen we aan bij een bekende passage uit een geschrift van Descartes over de methodiek van het wetenschappelijk denken, de Regulae ad directionem ingenii, waarin hij de kenmerken opsomt waaraan een gebied van ons weten moet voldoen om vatbaar te zijn voor mathematische behandeling. Die vatbaarheid bestaat wanneer het bestudeerde gebied kan worden onderworpen aan ordo of mensura, dat wil zeggen wanneer men de oordelen die men erover uitspreekt, kan rangschikken in deductieve ketens of wanneer men tussen de optredende grootheden kwantitatieve relaties kan vestigen die een algebraïsche behandelingswijze toelaten. Dit is een omschrijving die met enige wijziging en uitbreiding tot in onze tijd dienst kan doen: alles wat zich leent tot een van de twee behandelingswijzen, die we door de kenwoorden axiomatisering en algoritmisering kunnen aanduiden, wordt eo ipso getrokken binnen de sfeer der mathesis. Wiskunde toch beduidt veeleer een stijl van ons denken dan een gebied van ons weten en ze kan ook, onafhankelijk van de aard der behandelde stof, overal daar toepassing vinden waar men axiomata kan opstellen die uitgangspunt van deductieve redeneringen kunnen zijn en waar men eigenschappen of relaties van kwalitatieve of kwantitatieve aard kan voorstellen door symbolen, die aan een systeem van verbindingsregels, dat in gegeneraliseerde zin van het woord een algorithmus moge heten, kunnen worden onderworpen.

* ‘impopulariteit’: Tegen de impopulariteit die de wiskunde vooral in het interbellum had, heeft Dijksterhuis zich keer op keer verzet. Al in 1920 keerde hij zich in een artikel tegen de plannen om op middelbare scholen de aandacht voor de wiskunde in te perken, hoewel hij het idee had dat zijn protest niet veel zou uitrichten. Want, zo schreef hij, ‘de geest van de tijd schijnt vijandig te zijn aan de mathesis’ (‘Over wiskundig onderwijs’, in: Weekblad voor gymnasiaal en middelbaar onderwijs 17 (1920-1921) 947-968, in het bijzonder 968). Een kleine twintig jaar later was de situatie niet noemenswaard verbeterd; tegen het eind van de jaren dertig maakte de gedachte opgang om de wiskunde te verbannen van het lesrooster van het Gymnasium-alfa. Ook daar keerde Dijksterhuis zich tegen, nu in een Gids-artikel: ‘Haat tegen de wiskunde’, in: De Gids 102 (1938) iv, 347-350.

[p. 132]

Past men deze algemene beschouwingswijze toe op de natuurwetenschap der zeventiende eeuw, dan vinden we in hoofdzaak twee gebieden waarop de wiskunde in de omschreven zin onmiddellijk toepasbaar kon zijn en waarop ze dan ook inderdaad toegepast is. Het zijn de mechanica van vaste en vloeibare lichamen en de optica, twee vakken die te zamen op de eerste blik wellicht slechts een klein gedeelte van het gehele, hemel en aarde, levende en dode materie omvattende gebied der natuurwetenschap zullen schijnen te vormen, maar die, zoals het verdere verloop der geschiedenis zou leren, beide juist wegens hun vroegtijdige mathematische ontwikkeling voor dat geheel van fundamentele betekenis zijn geweest. Ik zal om het doel van dit artikel, dat niet bestaat in het nastreven van encyclopedische volledigheid, te bereiken, kunnen volstaan met de behandeling van een van deze twee gebieden; ik beperk me dus tot een schets van de groei der mathematische mechanica, van de wiskundige behandelingswijze dus van de verschijnselen van beweging en evenwicht.

Die wiskundige behandelingswijze dateert niet voor alle delen der mechanica eerst uit de zeventiende eeuw; er zijn integendeel twee van haar onderwerpen aan te wijzen waarop reeds lang voor die tijd wiskundige methoden zijn toegepast of die zelfs als onderdeel der wiskunde zijn beschouwd. Het zijn de kinematica van de eenparige beweging en de leer van het evenwicht. De eerste was, zonder dat er nog van een meer algemene behandeling van het bewegingsbegrip sprake was geweest, in de Griekse wiskunde gebruikt voor het voortbrengen van kromme lijnen en in de Griekse astronomie voor het beschrijven van de bewegingen der planeten. De tweede was reeds tot op zekere hoogte geaxiomatiseerd in de statische geschriften van Archimedes, waarin de leer van zwaartepunt en hefboom en die van de rustende vloeistoffen een mathematische basis had gekregen; op dit gebied was verdere vooruitgang bereikt in de dertiende eeuw in de school van Jordanus Nemorarius en in de vijftiende en zestiende door de Italiaanse mechanici.

In het begin van de zeventiende eeuw is men nu, op één aanstonds nader te behandelen uitzondering na, principieel nog niet tot een verdere uitbreiding van de mathematische behandelingswijze der mechanica gekomen; nog steeds zijn het alleen de eenparige beweging en het evenwicht die met enige exactheid in begripsbepaling, terminologie en bewijs kunnen worden behandeld, terwijl van alle meer gecompliceerde bewegingsverschijnselen, zoals val, worp en botsing, nog slechts een zeer onvolkomen kennis bestaat. Men zal als tegenvoorbeeld wellicht op de vondst van Kepler willen wijzen dat de planeten zich in ellipsen bewegen, welke beweging immers niet eenparig is, maar, nog afgezien van het feit dat Kepler juist een van hen is waarmee de nieuwe tijd zich aankondigt, moet erop gewezen worden dat hij in het verschijnsel der planetenbeweging toch ook juist het element van eenparigheid in het licht stelt: de voerstraal van de planeet naar de zon beschrijft een oppervlak dat evenredig is

[p. 133]

met de tijd; de perksnelheid is constant. Ook zal men wellicht Simon Stevin willen noemen en men wijst dan opnieuw iemand aan die, hoewel zijn sterkste produktiviteit nog in de zestiende eeuw valt, niettemin reeds thuishoort in de mathematische natuurwetenschap der zeventiende; maar bij nadere beschouwing blijkt toch ook hij, op één voor de ontwikkeling der dynamica fundamenteel axioma, dat van de onmogelijkheid van het perpetuum mobile, na, geheel te blijven binnen de banen die Archimedes voor de ontwikkeling der statica had aangegeven.

Zo is de toestand dus nog wanneer in 1608 Stevins Wisconstighe ghedachtenissen en in 1609 Keplers Astronomia nova het licht zien. Verplaatsen we ons nu echter, om van tevoren een overzicht te krijgen van het vele dat de zeventiende-eeuwse mechanica zou brengen, naar een tijdstip dat ongeveer tachtig jaren later ligt en dat een keerpunt beduidt in de geschiedenis van het denken: in 1687 verschijnen Newtons Philosophiae naturalis principia mathematica, waarin de stormachtige ontwikkeling van een wetenschap die in het begin der eeuw nog niet bestaan had, een voorlopige afsluiting vindt. Op alle punten blijkt de stand der dingen nu diepgaand gewijzigd te zijn: de kinematica van val en worp is nu geheel bekend; de dynamica van het stoffelijk punt is ontwikkeld; die van het vaste lichaam in beginsel gefundeerd; de verschijnselen van botsing, cirkelbeweging en slingerbeweging zijn bestudeerd. De axiomatisering is reeds zover gevorderd dat Newton met drie axiomata of bewegingswetten kan volstaan voor de deductie van het gehele systeem der rationele mechanica. Met opheffing van de eeuwenoude schijnbaar onverzoenlijke tegenstelling tussen aardse en hemelse verschijnselen, die de leer van Aristoteles had gevestigd, zijn val en planetenbeweging onder één gezichtspunt samengevat en onderworpen aan de algemene mechanische axiomata. Tegelijkertijd heeft de mechanica haar stempel gedrukt op het gehele onderzoek der anorganische natuur; mechanistische verklaring van alle natuurverschijnselen is aan het eind der zeventiende eeuw bij alle onderlinge meningsverschillen tussen filosofen of fysici over het wezen der materie, over vacuüm of plenum, over atomistiek of energetica, over werking op afstand, beïnvloeding door een medium of bewegingsopdracht door botsing, een algemeen aanvaard werkprogramma geworden; de gebieden waarop dit programma een begin van uitvoering heeft gevonden, astronomie en optica, zijn reeds tot sterke bloei gekomen en de takken der natuurwetenschap die bij de andere achter staan in ontwikkeling, warmteleer, magnetisme en elektriciteit en vooral chemie, zijn juist diegene waarop men noch met mechanica in het bijzonder noch met wiskunde in het algemeen nog iets had kunnen beginnen.

Wel zelden heeft in de geschiedenis een tak van wetenschap zich in zo korte tijd tot een zo grote hoogte ontwikkeld en daarbij een zo sterke invloed op het wetenschappelijk denken en op de wereldbeschouwing uitgeoefend. Het is een historisch probleem van de eerste orde dit verschijnsel in zijn voorbereiding en ontplooiing nauwkeuriger te leren kennen en te begrijpen. Wanneer

[p. 134]

dan daarbij blijkt, wat ik aannemelijk hoop te maken, dat die sterke groei der mechanica niet alleen gepaard is gegaan met haar mathematisering maar dat zij daarvan het onmiddellijk gevolg is geweest, dan zal meteen aan het denkbaar duidelijkste voorbeeld de historische betekenis in het licht zijn gesteld die aan de intrede der wiskunde in de natuurwetenschap moet worden toegekend.

Beziet men, om tot de oplossing van het gestelde probleem te komen, de zeventiende-eeuwse mechanica in vergelijking met die van vroegere eeuwen vanuit de beide cartesiaanse gezichtspunten van ordo en mensura, dan trekt vooreerst onmiddellijk, dat wil zeggen vanaf de eerste jaren der eeuw, de sterke ontwikkeling van haar algoritmisering de aandacht. Men kan die ontwikkeling in algemene zin zo omschrijven dat de mechanica gebruik leert maken van nieuw ontdekte of teruggevonden mathematische methoden ter behandeling van de continu veranderlijke grootheid, die in het eind der eeuw tot de uitvinding der infinitesimaalrekening zouden leiden. Om deze uitspraak te verduidelijken moet ik even tijd nemen voor een korte historisch-mathematische uitweiding.

Noch de Griekse wiskunde, noch de uit Indische en Arabische bronnen gevoede algebra der Renaissance heeft het vermogen bezeten tot mathematische behandeling van de continue veranderlijkheid. De gedachte om de wijze waarop een continu veranderlijke grootheid op zeker ogenblik bezig is haar waarde te wijzigen, kwantitatief te fixeren door een nieuwe grootheid, die men in het algemeen de intensiteit van de verandering der eerst beschouwde zou kunnen noemen, lag geheel buiten beider gezichtskring; geen van beide bijvoorbeeld zou hebben kunnen aangeven, wat men te verstaan heeft onder de snelheid van een niet-eenparige beweging op zeker ogenblik of onder de richting van een kromme lijn in zeker punt. Mathematisch beduidt dit dat de beide genoemde fasen der wiskunde het grondbegrip der differentiaalrekening missen, wat tot uiting komt èn in de talloze fouten die er in de kinematica der valbeweging worden gemaakt ten gevolge van de verwarring van de snelheid op zeker ogenblik en de gemiddelde snelheid gedurende zeker tijdvak èn in de omslachtige, niet tot het wezen der zaak doordringende wijze waarop raaklijnen aan kromme lijnen worden bepaald. Dit gemis heeft, althans voor de Griekse wiskunde, die toch onder de verschillende stromingen die in de Westeuropese wiskunde der zeventiende eeuw samenvloeien, de overheersende blijft, een diepe grond; zij toch is in de periode van haar snelste ontwikkeling en van haar definitieve axiomatisering onder de sterke invloed gekomen van de filosofische opvattingen van Plato, waarvan de wezenlijke eigenschappen, voorzover ze ons onderwerp betreffen, weer zijn af te leiden uit de theorieën van zijn en veranderen der Eleatische school, die door Zeno van Elea toepassing op de wiskunde hadden gevonden. Volgens die theorie komt alleen aan het onveranderlijke zijn realiteit toe terwijl worden en veranderen slechts een onwezenlijke schijn beduiden. Het is daarmee in overeenstemming dat in het systeem van Plato de wiskunde zich bezighoudt

[p. 135]

met de onveranderlijke ideële mathematische vormen, die hun plaats hebben tussen de schijnwereld die wij waarnemen en het rijk der ideeën; ontstaan en vergaan is bij die vormen uitgesloten en Plato verbant dan ook met volkomen consequentie uit de meetkunde het begrip der constructie in de zin van het voortbrengen van een figuur. Van deze zienswijze nu is de Griekse wiskunde zoal niet de volkomen verwerkelijking dan toch de duidelijke afspiegeling. Euclides vermijdt toepassing van het bewegingsbegrip in de meetkunde zolang hij het enigszins doen kan en in de eenparige bewegingen, die andere mathematici in hun wiskundige redeneringen toelaten en die Plato zelf in zijn ideële astronomie gebruikt, overheerst toch altijd het constante element der eenparigheid het denkbeeld van verandering, dat aan de beweging eigen is.

Nu kon Plato zo streng theoretisch te werk gaan omdat voor hem de enige realiteit in de ideeën ligt, terwijl de wereld die de natuurlijke mens de werkelijke noemt niets anders is dan een spel van schaduwen. Voor Aristoteles echter vormt dat schaduwenspel zelf de werkelijkheid die hij wil onderzoeken en het probleem der verandering, dat voor Plato niet bestond, wordt het centrale probleem van zijn filosofie, dat hij door de onderscheiding van het potentiële en het actuele zijn tracht op te lossen. Onder zijn invloed wordt in de peripatetische wijsbegeerte de studie der beweging, dat is het algemene begrip dat alle soorten van verandering, zowel kwalitatief als kwantitatief, omvat en waarvan de verandering van plaats, de motus localis, slechts een bijzonder geval is, het essentiële element der fysica, wat tot uiting komt in de zegswijze der scholastiek: Ignorato motu ignoratur natura.^*

Van al de filosofische beschouwingen over de verandering die uit de aristotelische opvatting zijn voortgevloeid is nu voor ons doel voornamelijk de behandeling van de vraag van belang hoe men zich de intensiteitsverandering van een kwaliteit moet denken. In de scholastiek treedt dit probleem het eerst op in deze formulering hoe de caritas in een mens kan toe- of afnemen en hoe ze dus op verschillende ogenblikken verschillende waarden kan hebben. Hierover vormen zich twee hoofdrichtingen van opvatting, elk met nog weer fijnere schakeringen, waarvan de eerste steeds een principieel verschil blijft maken tussen versterking en verzwakking van een kwaliteit aan de ene kant en toe- of afname van een kwantiteit aan de andere, terwijl de tweede de nadruk legt op de analogie tussen de beide verschijnselen en daardoor de voor de natuurwetenschap zo belangrijke kwantitatieve behandeling van kwaliteiten voorbereidt. De tweede opvatting is vooral tot ontwikkeling gekomen in de Parijse school der terministen, die in de veertiende eeuw onder leiding van Buridan, Albert van Saksen en Oresme in oppositie tegen Aristoteles zulke belangrijke denkbeelden over mechanica en astronomie heeft ontwikkeld. Daarbij heeft Oresme, die in 1382 als bisschop van Lisieux stierf, voorzover onze tegenwoordige kennis reikt als eerste een hulpmiddel toegepast dat voor het gehele wetenschappelijke denken van onafzienbare betekenis zou blijken te zijn: om de verandering van een kwaliteit duidelijk voor ogen te voeren stelt

* ‘Ignorato motu’: ‘Als de beweging niet wordt begrepen, wordt de natuur niet begrepen.’

[p. 136]

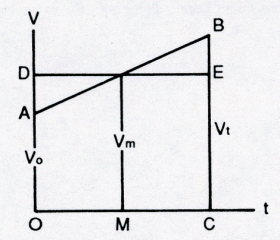
hij iedere achtereenvolgens optredende intensiteit voor door een lijnstuk, de latitudo, waarvan de lengte de waarde der intensiteit aangeeft en dat wordt uitgezet loodrecht op de extensio, dat is de uitbreiding in ruimte of tijd van het subjectum dat met de veranderlijke kwaliteit is aangedaan. Beschouwen we bijvoorbeeld het geval van een extensio in de tijd, dan wordt dus bijvoorbeeld een veranderlijke caritas, om het in onze tegenwoordige taal te zeggen, beschouwd als functie van de tijd en grafisch voorgesteld op een assenstelsel, waarin de tijd als abscis en de intensiteit der caritas als ordinaat fungeert. Oresme bestudeert nu allerlei verschillende mogelijkheden van verandering aan het voorbeeld van de snelheid van een veranderlijke beweging, een kwaliteit waarvan de intensiteit op een gegeven ogenblik volgens hem wordt bepaald door de weg die in een op dat ogenblik aanvangend tijdvak van gegeven duur zou worden afgelegd wanneer de beweging plotseling eenparig werd; is de snelheid uniformis, eenparig, dan is de grafiek een rechte, evenwijdig aan de extensio, die met de assen en de laatste latitudo een rechthoek bepaalt waarvan de oppervlakte, de mensura der kwaliteit, blijkbaar de afgelegde weg voorstelt; is ze uniformiter difformis, eenparig veranderlijk, dan vindt men een hellende snelheidsrechte, een trapezium, als ordinatenoppervlak en een mensura die het produkt is van de tijd en de latitudo van het middelste ogenblik. Is ze niet eenparig veranderlijk, difformiter difformis, dan wordt de snelheidslijn gebogen. Het blijkt nu dat Oresme, althans voor het geval van de motus uniformiter difformis, volkomen helder heeft beseft dat de mensura, de oppervlakte van de ordinatenfiguur, evengoed de afgelegde weg voorstelt als bij de motus uniformis en het lijkt niet gewaagd te onderstellen dat hij ook voor het algemene geval van de motus difformiter difformis aan de mensura, die wij tegenwoordig de integraal van de snelheid naar de tijd noemen, deze betekenis zal hebben gehecht. In geheel algemene termen spreekt hij voor iedere eenparig veranderlijke kwaliteit de eigenschap uit, die de regel van Oresme behoort te heten en die voor de motus localis aldus luidt: de weg, in zekere tijd afgelegd in een eenparig veranderlijke beweging, is gelijk aan de weg die in dezelfde tijd zou worden afgelegd in een eenparige beweging, waarvan de snelheid voortdurend gelijk is aan die van de veranderlijke beweging op het middelste ogenblik van de beschouwde tijd.^* Of hij deze regel ook op andere kwaliteiten dan de snelheid heeft toegepast, of hij dus bijvoorbeeld ook de caritas naar de tijd heeft geïntegreerd, wat zoiets als de goede werken zou hebben moeten opleveren die in het beschouwde tijdvak zijn verricht, is helaas niet bekend.

Het behoeft de lezer niet te verontrusten dat ik, hoewel eigenlijk bezig met de mathematisering van de mechanica in de zeventiende eeuw, nog altijd vertoef bij de Parijse scholastici der veertiende. Want terwijl ik schrijf over het werk van Oresme, behandel ik tegelijkertijd al het fundamentele denkmiddel dat de zeventiende-eeuwse mechanica in de handen van Stevin, Galilei, Beeckman, Descartes en Huygens tot ontwikkeling zal brengen, dat de meet-

* Deze uiteenzetting wordt duidelijker als de figuur wordt bijgevoegd die Dijksterhuis later in De mechanisering van het wereldbeeld, p. 216 van de regel van Oresme liet opnemen:

[p. 137]

kundig-aanschouwelijke voorstelling mogelijk zal maken van de symbolische bewerkingen der infinitesimaalrekening en dat in onze tijd, na een periode van overheersing van symbolische en daardoor onvermijdelijk enigszins machinale methoden, sterker dan ooit tevoren toepassing vindt, niet alleen in de wiskunde en de natuurwetenschap maar ook op tal van andere gebieden van ons weten, waaronder de meest uiteenlopende: de grafische voorstelling van een functionele afhankelijkheid. Het zal hierdoor duidelijk zijn welk een keerpunt in de geschiedenis Oresmes theorie de latitudinibus formarum beduidt; hier lukt wat de Griekse wiskunde niet tot stand had kunnen brengen, maar waarvan alle verdere ontwikkeling van het wiskundig denken èn op zichzelf beschouwd èn in zijn toepassing op de natuur afhing: de mathematische fixering van het begrip der continue veranderlijkheid. Het gelukte door de kunstgreep een primaire veranderlijkheid als gegeven te beschouwen en alle andere in haar betrekking tot deze te omschrijven. Voor die primaire veranderlijke was natuurlijk de tijd, opgevat als in zich zelf gelijkmatig vloeiend, aangewezen; de vondst van Oresme bestond hierin dat hij de extensio van het subject in de tijd aanschouwelijk maakte als extensio in de ruimte, waardoor hij op één ogenblik naast elkaar kon plaatsen wat op één plaats na elkaar gebeurde. De historie der natuurwetenschap heeft lange tijd geen goed woord overgehad, noch voor Aristoteles, noch voor de scholastiek en inderdaad kan men niet ontkennen dat hun wijze om de natuur te beschouwen in vele opzichten onvruchtbaar is gebleken. Nu we hier echter over de grote opbloei der natuurwetenschap in de zeventiende eeuw spreken, mag er wel eens aan herinnerd worden dat we aan Aristoteles het begrip van een natuurwetenschap, dat voor Plato eigenlijk niet bestond, te danken hebben en dat de scholastiek het wiskundige hulpmiddel schiep dat ruim twee eeuwen later de sterke ontwikkeling der mechanica mogelijk zou helpen maken.

Want inderdaad, het heeft ruim twee eeuwen geduurd voor men geleerd heeft van de grafieken van Oresme een werkelijk vruchtbaar gebruik te maken. Stevin gebruikt ze in 1585 in de hydrostatica, Galilei leidt er in de eerste jaren der zeventiende eeuw de wet mee af die voor vrije val uit rust het verband uitdrukt tussen de afgelegde weg en de daaraan bestede tijd, Descartes en Beeckman vinden in 1618 te Breda gezamenlijk hetzelfde resultaat, waarbij Beeckman zeer waarschijnlijk het fysisch beginsel der afleiding, namelijk het behoud van een eenmaal voortgebrachte snelheid, heeft aangegeven en Descartes het mathematische hulpmiddel. Dat er tussen deze toepassingen en de theoretische behandeling bij Oresme een continue samenhang bestaat, is, gezien de sterke verspreiding van zijn denkbeelden in de scholastiek en de opleiding die niet alleen Descartes maar ook Galilei had genoten, nauwelijks meer voor twijfel vatbaar. Verwonderlijk kan het alleen lijken dat een methode van zo grote draagwijdte eerst ruim twee eeuwen na haar ontstaan plotseling allerwege een zo vruchtbare toepassing vindt.

Dat is nu echter bij nadere beschouwing zo verwonderlijk niet. Men moet

[p. 138]

namelijk ten eerste bedenken dat voor het toepassen der grafische methode bij alle veranderingen die niet uniformiter difformis zijn, en voor het voortbouwen op de resultaten die men er mee verkrijgt ook in de eenvoudigere gevallen, een veel grotere mathematische ontwikkeling nodig was dan er in West-Europa vóór de zestiende eeuw bestond. De wiskunde is pas op hoger peil gekomen toen men in de zestiende eeuw de Griekse mathematische schrijvers in vertalingen en weldra ook in het origineel had leren bestuderen en eerst in het begin der zeventiende eeuw is de geest der Griekse wiskunde, die zowel het vernuftige uitvindingsvermogen insluit als de gave der heldere uiteenzetting, voldoende vaardig geworden over de mathematici van West-Europa om de meetkundige behandeling van het veranderlijke tot volle ontplooiing te brengen. En ten tweede is voor de ontwikkeling van de mathematische fysica nog iets anders nodig dan de schepping van een mathematisch instrument en een mathematische taal: de fysische begripsvorming brengt eerst het materiaal aan dat met dat instrument wordt behandeld en in die taal wordt beschreven. Het komt niet zelden voor dat de natuurkunde aan een wiskundig hulpmiddel eerst vele jaren na zijn ontstaan behoefte heeft: de niet-euclidische meetkunden en de matrixtheorie zijn er twee sprekende voorbeelden van.

Over die begripsvorming in de mechanica aanstonds nader; eerst nog iets over het gebruik van de formele wiskundige hulpmiddelen in de tijd toen de mathematische ontwikkeling al wel de nodige hoogte had bereikt. De heterogeniteit van hun oorsprong maakt het begrijpelijk dat de toegepaste denkwijzen, de Griekse methode van onderzoek en uiteenzetting, de aan de scholastiek ontleende grafische voorstelling der veranderlijkheid, waarbij dan nog de door Indo-arabische invloeden gewijzigde rekentechniek en de pas geschapen symbolische algebra kwamen, zich niet onmiddellijk tot een harmonisch geheel lieten versmelten. In het bijzonder kan men in de zeventiende eeuw bij alle bewondering en verering die de grote mathematici voor hun Griekse voorgangers aan de dag leggen, een duidelijk streven opmerken zich van de langzamerhand als belemmering gevoelde eigenaardigheden der euclidische methode los te maken, wat op enkele punten met een verloochening van de meest fundamentele beginselen van die methode gepaard ging. Dit verschijnsel doet zich voornamelijk voor op een gebied dat de wiskunde èn in haar eigen ontwikkeling èn in haar toepassing op de natuur telkens weer moet betreden en dat zij in het bijzonder bij de behandeling van de continue veranderlijkheid nooit vermijden kan, het gebied der oneindige processen.

Dat de studie van de continue veranderlijkheid inderdaad onvermijdelijk tot oneindige processen voert, kan men zich onmiddellijk aan enkele voorbeelden duidelijk maken. Men behoeft daartoe slechts een poging te doen exact te omschrijven wat men verstaat onder de snelheid van een veranderlijke beweging op zeker ogenblik of aan te geven hoe men tot de berekening van de mensura van een grafiek komt. In het eerste geval is men geneigd de snelheid

[p. 139]

op zeker ogenblik te definiëren als het quotiënt van de weg die in een klein tijdvak dat op het beschouwde ogenblik volgt, wordt afgelegd en de duur van dat tijdvak, maar als men om een grotere nauwkeurigheid te verkrijgen die duur steeds kleiner gaat nemen, wordt men ad infinitum gevoerd, omdat men bij ieder tijdvak een ander kan aangeven dat kleiner is. En in het tweede geval zou men de figuur wel graag willen beschouwen als som van smalle rechthoeken, wanneer het maar mogelijk was een kromme lijn uit rechte lijnstukjes samen te stellen. Door rechthoekjes te beschrijven bereikt met dus slechts een benadering; tracht men die benadering te verbeteren door de rechthoeken smaller te nemen, dan overschrijdt, mèt de onbeperkte afname van de breedte, het aantal rechthoeken iedere willekeurig aangegeven waarde, terwijl toch in geen enkel stadium van de bewerking de opvulling met rechthoeken gelukt. Weer ziet men dus het duizelingwekkende oneindige voor zich. En toch kan men de breedte der rechthoeken hier evenmin nul laten zijn als men bij de snelheidsbepaling het beschouwde tijdvak zonder duur kon kiezen. Want door juxtapositie van lijnstukken krijgt men geen oppervlak en in een tijdvak dat geen duur heeft, wordt geen weg afgelegd.

Ook de Griekse wiskunde heeft in de loop van haar ontwikkeling de twee denkmoeilijkheden die hier aan concrete voorbeelden zijn toegelicht, maar waarvan het algemeen karakter onmiddellijk duidelijk zal zijn, onder ogen moeten zien. Van de eerste, die de mathematische fixering der momentane veranderlijkheid betreft, is zij zich bewust geworden in de bewegingsparadoxen van Zeno van Elea en de invloed van zijn kritiek, die men op zovele plaatsen in de Griekse wiskunde kan vermoeden, is blijkbaar sterk genoeg geweest om het hele probleem uit te sluiten van de opbouw der mathesis. De tweede, die bij de berekening van de oppervlakten van kromlijnig begrensde figuren optreedt, heeft zij opgelost op een zeer strenge wijze, die echter, zoals strengheid altijd doet, tot moeilijke en langdurige redeneringen voert. Die oplossing was zo radicaal als ze maar zijn kon: het woord oneindig werd uit het wiskundig vocabularium geschrapt en de eis werd gesteld om, wanneer na een eindig aantal benaderingen het resultaat intuïtief kon worden voorvoeld, door een redenering uit het ongerijmde, waarin geen termen mochten voorkomen die op het oneindige betrekking hadden, de juistheid van dat resultaat aan te tonen.

Nu bestaat er echter altijd naast de officiële wiskunde van de publikaties waarvoor exactheid in uitdrukking en bewijs het enig ideaal is en die daarom ook vaak de weg waarlangs de vondst is gedaan opzettelijk en zonder enige tegemoetkoming aan de behoeften van de lezer verdoezelt, een meer officieuze mathematische uitvindingskunst, die allerlei niet geheel te verantwoorden gedachtengangen niet schuwt, wanneer ze maar tot het beoogde doel voeren. Bij de Grieken was dat niet anders. Archimedes, die in zijn officiële werken de strengheid zelve is en die daarin het woord oneindig niet in de mond zou durven nemen, blijkt in de intimiteit van zijn werkkamer bij de bepaling van

[p. 140]

oppervlakten wel degelijk de stap te hebben gedaan die het natuurlijke, voor de gevaren van het oneindige nog niet gewaarschuwde denken ook altijd doen wil: hij heeft een oppervlak beschouwd als de som van al zijn lijnen en op grond van die logisch onhoudbare opvatting heeft hij dingen gevonden die hij misschien nooit zou hebben ontdekt langs de weg waarop hij ze daarna exact bewijst.

Wat nu echter bij Archimedes nog in het geheim van de werkplaats geschiedde, wordt in het begin van de zeventiende eeuw de methode der officiële wiskunde. Kepler beschouwt een cirkel ronduit en zonder dat dit een afkorting is van een meer correcte spreekwijze, als een veelhoek met oneindig veel zijden. Cavalieri laat de mathematische atomistiek van de pre-euclidische meetkunde herleven door een oppervlak te beschouwen als de som van zogenaamde indivisibilia, van ondeelbare oppervlaksatomen. Wat dat eigenlijk is, lijnstukken of smalle rechthoeken, wordt men niet gewaar en men kan dat ook nooit gewaarworden omdat het ene zo ongerijmd zou zijn als het andere. De wiskunde heeft die indivisibilia weldra overgenomen onder de naam van infinitesimale of oneindig kleine grootheden. Dat was een zinledige zegswijze, die daarom bijzonder geschikt was om de eigenlijke mathematische moeilijkheid weg te doezelen; ze is daarvoor dan ook tot in de negentiende eeuw druk en tot groot voordeel van de ontwikkeling der mathematische techniek gebruikt. Eerst sedert een eeuw is de wiskunde teruggekeerd tot de strenge beginselen der Grieken, waarbij ze wel bleef spreken van oneindig kleine grootheden, maar nu bij wijze van afkorting van een langere, geheel correcte manier van uitdrukken.

Het spreekt natuurlijk wel vanzelf dat de ontwikkeling van de wiskundige opvattingen inzake het oneindige niet zo eenvoudig en vlot verlopen is als ik het hier ter wille van de overzichtelijkheid vertel. De toepassing van de nieuwe en onstrenge methoden moest natuurlijk bij mathematici die in de ideologie van de Griekse wiskunde waren opgevoerd, tot gewetensconflicten voeren en het zijn juist de grootste figuren der zeventiende eeuw waarbij we zulke conflicten zien optreden. Galilei, Huygens en Newton volgen alle drie het voorbeeld van Archimedes om in de publikaties alle sporen van het uitvindingswerk te overpleisteren met een correct-euclidische façade. Huygens laat er zich in zijn particuliere aantekeningen over uit dat hij het eigenlijk overbodig vindt, maar als het Horologium oscillatorium in 1673 verschijnt, blijkt het geheel in de streng-euclidische stijl geschreven te zijn. En Newton heeft in 1687 nog hele passages uit de Principia die met behulp van de nieuwe analytische methoden waren gevonden, in de taal der Griekse wiskunde overgebracht. Zo sterk werkte de invloed van de Stoicheiotes,^* waaraan immers zelfs onze tijd zich nog niet heeft ontworsteld, nog na.

De veranderde houding ten aanzien van het oneindige die in het bovenstaande kort werd geschetst, is, hoe belangrijk ook, natuurlijk niet de enige factor geweest die de sterke opbloei der zeventiende-eeuwse wiskunde heeft

* ‘Stoicheiotos’: letterlijk: de man van de Elementen, bijnaam voor Euclides.

[p. 141]

bevorderd. Twee andere vermeldde ik al terloops: de ontwikkeling der rekentechniek, die sterk in de hand was gewerkt door de invoering der decimale breuken door Simon Stevin en door de uitvinding der logaritmen door Napier; en de schepping der symbolische algebra door Viète, die vooral van belang werd nadat Descartes met haar hulp aan de analytische methoden der Griekse wiskunde een groter terrein van toepassing had geopend. In de analytische meetkunde werd het probleem in een willekeurig punt van een kromme waarvan de vergelijking gegeven is de raaklijn te trekken, het meetkundig-algebraïsche analogon van de snelheidsbepaling in de kinematica. Steeds meer vragen bepalingen van oppervlakten, inhouden en zwaartepunten, die in wezen alle verwant zijn met de bepaling van de mensura van een grafiek, de aandacht. En tegen het einde der eeuw vloeien al die verschillende stromingen van onderzoek in wiskunde en mechanica samen in de vondst die het karakter der wiskunde definitief zou bepalen en die haar toepassing op de natuurwetenschap eerst tot de hoogste graad van vruchtbaarheid zou opvoeren, de uitvinding van de differentiaal- en integraalrekening door Newton en Leibniz.

Wat die vondst in beginsel inhield is na het voorafgaande in korte woorden te zeggen. Boven bleek reeds dat er, als men de snelheid van een veranderlijke beweging op zeker ogenblik wil bepalen door het quotiënt van weg en tijd te berekenen over een klein tijdvak dat op het beschouwde ogenblik begint, een moeilijkheid optreedt omdat men dat tijdvak onbeperkt kan en moet verkleinen terwijl het toch nooit nul mag zijn, terwijl zich een analoog probleem voordoet bij de bepaling van de mensura van een grafiek. Wanneer nu echter blijkt dat er in het eerste geval een vast getal bestaat waartoe men door voldoende verkleining van het beschouwde tijdvak de berekende gemiddelde snelheid zo dicht kan laten naderen als men zelf maar wil en dat men in het tweede geval in dezelfde zin van het woord een grenswaarde voor de som der beschouwde rechthoeken kan aangeven, dan kan men die grenswaarden respectievelijk als de snelheid van de beweging op het beschouwde ogenblik en als de oppervlakte van de kromlijnig begrensde figuur beschouwen. De bepaling van die grenswaarden langs de weg der berekening vormt nu het onderwerp der differentiaal- en integraalrekening; men vindt de snelheid door differentiëren van de weg naar de tijd, de mensura van een grafiek door integratie van de ordinaat.

Tussen beide bewerkingen bestaat nu een eenvoudig verband; wanneer men in een grafiek de horizontale extensio, dus de abscis, met een klein bedrag laat aangroeien, verandert ook de mensura, of zoals we thans kunnen zeggen, de integraal. Die verandering is voor een gegeven aangroeiing van de abscis des te sterker, naarmate de eindordinaat y groter is. Bepaalt men nu op dezelfde wijze waarop men de momentane snelheid van een veranderlijke beweging vindt, de intensiteit van deze verandering, dan blijkt deze juist door de waarde van die eindordinaat y te worden aangegeven. Zoals dus enerzijds de mensura

[p. 142]

uit y door integreren ontstaat, vindt men anderzijds y door differentiëren uit de mensura terug. Integreren en differentiëren, hoe verschillend ook van oorsprong, blijken elkaars omgekeerde bewerkingen te zijn, zoals optellen en aftrekken.

De manier waarop ik heb getracht de begrippen differentiëren en integreren, vondsten van onafzienbare historische betekenis, voor niet-mathematici te verduidelijken, voldoet evenmin aan de eisen van mathematische exactheid als aan die van historische juistheid. Om aan de eerste te voldoen zou ik het begrip grenswaarde nader hebben moeten omschrijven, wat de zaak wellicht niet duidelijk zou hebben gemaakt; om de tweede te bevredigen, zou ik weer over oneindig kleine grootheden hebben moeten spreken, waardoor het hoogstens een schijn van begrijpelijkheid zou hebben kunnen krijgen. Nu achteraf kan ik het spraakgebruik van het oneindig kleine echter niet meer vermijden, omdat de grondleggers der infinitesimaalrekening het met zoveel succes hebben toegepast. Voor Leibniz is een integraal inderdaad een som van oneindig veel oneindig kleine rechthoeken, waarin men het woord oneindig klein niet moet opvatten in de figuurlijke of potentiële betekenis van naderend tot nul waarin wij tegenwoordig zeggen dat een grootheid oneindig klein wordt, maar in de actuele betekenis van iets dat niet nul is en niet eindig. Zoiets bestaat in het getallensysteem waarvan de analyse zich bedient niet en we ontmoeten hier dus een typisch voorbeeld van het element van irrationaliteit dat aan sommige wiskundige theorieën in de eerste fase van hun bestaan eigen is. Men kan zich inderdaad in onze tijd, nu wij de hier te pas komende begrippen en methoden helder hebben leren doorzien, nauwelijks meer voorstellen hoe Leibniz, Newton en hun eerste aanhangers erin geslaagd zijn zelf hun nieuwe methode te begrijpen en toe te passen. Alle transparante helderheid, die men onwillekeurig als wezenlijk kenmerk van de wiskunde beschouwt omdat ze eigen is aan haar voltooide bouwsels, is in de beginjaren van de infinitesimaalrekening ver te zoeken. Wat men waarneemt is, zou men kunnen zeggen, meer dionysisch dan apollinisch van aard, meer uiting van een half onbewuste scheppingsdrang van enkele mathematische genieën dan heldere en doelbewuste redenering. Slechts een sterk intuïtief gevoel voor mathematische juistheid heeft de eerste beoefenaren der nieuwe methode kunnen bewaren voor bijna al de dwalingen waartoe het oneindige het zogenaamde gezonde mensenverstand, met de vooroordelen waarvan het spot, zo gemakkelijk verleidt. Het is geen wonder dat alleen de grootste mathematici van die tijd met zekerheid het werktuig hebben kunnen hanteren dat men tegenwoordig aan de eerste-jaarsstudent en weldra aan de schooljongen in handen geeft.^*

Ik moet nog een enkele opmerking maken over het verschil tussen de methoden van Newton en Leibniz op het gebied der infinitesimaalrekening. Bij Newton is alles gebaseerd op het aan de mechanica ontleende snelheidsbegrip; wanneer een grootheid x met de tijd verandert, wordt de veranderings-

* ‘schooljongen’: In de jaren twintig is een uitvoerige discussie gevoerd over de vraag of onderdelen van de hogere wiskunde, in het bijzonder de differentiaal- en integraalrekening, opgenomen moesten worden in het lesprogramma van de hbs. Dijksterhuis behoorde tot de voorstanders en in de jaren dertig is het vak ook op de hbs ingevoerd.

[p. 143]

snelheid, aangeduid door ẋ, de fluxie van deze vloeiende grootheid, deze fluens, genoemd. Hangt een andere grootheid y weer van x af, dus middellijk van de tijd, dan geeft het quotiënt ẋ/ẋ de verhouding van de gelijktijdige veranderingssnelheden van y en x aan; het is het equivalent van wat wij tegenwoordig het differentiaalquotiënt van y naar x noemen. Bij Leibniz daarentegen staat het begrip differentiaal op de voorgrond. Wat dat bij hem beduidt is weer moeilijk in klare woorden te zeggen. Het is, zoals het woord zegt, een verschil, maar dan een verschil van twee onmiddellijk op elkaar volgende waarden van een continu veranderlijke grootheid, wat echter niets betekent omdat het juist in het wezen der continuïteit ligt dat er geen onmiddellijke opvolging van waarden in voorkomt. Toch heeft de opvatting van Leibniz een zeer heilzame invloed op de ontwikkeling van de wiskunde en de mathematische fysica uitgeoefend. Leibniz, die een der eersten geweest is die het grote belang van een goede verzorging van de mathematische symboliek helder heeft beseft, heeft namelijk in de keuze van zijn notaties op het gebied der infinitesimaalrekening een zo gelukkige greep gehad dat de wiskunde zich geheel naar zijn voorstellen heeft gericht, terwijl de fluxienotatie alleen nog maar in de mechanica voortleeft. Van hem is de notatie dx voor de differentiaal of oneindig kleine aangroeiing van x, waarvan de waarde vooral bestaat in de analogie die er tussen sommige rekenregels voor het symbool d en de regels der gewone algebra bestaat; van hem is het symbool ∫ ydx voor een integraal, waarin ∫ een somteken beduidt en de dx de basis van de opvolgende oneindig smalle rechthoekjes, die de opvolgende waarden van y tot hoogte hebben. De differentiaal van deze integraal is nu weer ydx en de integraal is dus een som van differentialen.

Hoe nu eigenlijk de techniek van deze differentiaal- en integraalrekening is kan ik hier niet gaan uiteenzetten en het doet voor mijn doel ook eigenlijk niet ter zake. Hoofdzaak is dat men nu in beginsel kan inzien hoe de grafische methode, die zich uit de theorie van Oresme had ontwikkeld en die zich van de meetkundige terminologie en de meetkundige resultaten van de Griekse wiskunde moest bedienen, nu kon worden omgezet in symbolische rekenwijzen.

Door deze vondst, die de mathematische behandeling der veranderlijkheid in analytische vorm mogelijk maakte, gaf de wiskunde aan de natuurkunde, die immers de veranderingen bestudeert die we in de stoffelijke wereld zien optreden, juist datgene waaraan zij het sterkst behoefte had. Het was de mechanica, de leer van die meest aanschouwelijke veranderingen die de bewegingen der materiële lichamen ons te zien geven, die daarvan het eerst en het meest profiteerde. Immers met behulp van de differentiaalrekening kon men nu uit het verloop van een grootheid in de tijd tot de kennis van haar momentane veranderingssnelheid komen, terwijl omgekeerd de integraalrekening uit de wijze waarop de veranderingssnelheid van de tijd afhing, het

[p. 144]

verloop van de grootheid zelve leerde terugvinden. De infinitesimaalrekening deed echter in de loop van haar ontwikkeling meer dan dit. In het bijzonder gaf zij de oplossing van bepaalde probleemgroepen, die, in woorden geformuleerd, voor een niet-wiskundige aanvankelijk volkomen onoplosbaar moeten schijnen omdat zij de indruk maken een logische cirkelgang te bevatten. Het zijn bijvoorbeeld die problemen waarin het verloop van de waarde van een grootheid wordt gevraagd, wanneer de factoren die haar verandering bepalen van haar eigen waarde afhangen. Men denke bijvoorbeeld aan een stoffelijk punt dat valt, maar dat daarbij een luchtweerstand ondervindt die op ieder ogenblik evenredig is met de snelheid die het vallende punt dan heeft. Hierbij is dan voortdurend de momentane snelheid beïnvloed door de luchtweerstand op alle vorige tijdstippen, terwijl men voortdurend de snelheid moet kennen om de luchtweerstand te bepalen. Mathematisch geformuleerd voeren zulke problemen tot de zogenaamde gewone differentiaalvergelijkingen, dat zijn vergelijkingen waarin naast een onbekende grootheid, die bijvoorbeeld functie van de tijd is, ook haar fluxie of veranderingssnelheid of eventueel de fluxie van de fluxie optreedt. Gelukt het nu zulk een vergelijking op te lossen, dan is daardoor de schijnbare logische cirkelgang toch binnen het bereik der mathematische methode gebracht. Het bleek nu al spoedig dat het vooral de differentiaalvergelijkingen waren waaraan de fysica voor de beschrijving der natuurverschijnselen en voor de oplossing van haar problemen behoefte had; echter, die differentiaalvergelijkingen waren in vele gevallen van een moeilijker type dan de gewone, omdat bij deze de onbekende grootheid slechts wordt beschouwd in haar afhankelijkheid van een enkele variabele, terwijl zij in de regel van meer dan één veranderlijke grootheid afhankelijk zal zijn. Dat voert tot de zogenaamde partiële differentiaalvergelijkingen. Het is echter moeilijk hiervan veel meer te vertellen zonder werkelijk wiskundige redeneringen te houden. Om dezelfde reden kan ik niet meer dan de naam vermelden van een andere tak der infinitesimaalrekening die in de achttiende eeuw naast de leer der differentiaalvergelijkingen en mede tot groot nut der mechanica werd ontwikkeld. Het is de zogenaamde variatierekening, waarin men bijvoorbeeld het verloop van een werkelijk in de natuur optredende beweging leerde vergelijken met andere fictieve bewegingen, die onder weinig veranderde omstandigheden verliepen. Door al deze wiskundige vondsten en hun toepassingen hebben vooral de Zwitserse wiskundigen, de familie Bernoulli en Leonhard Euler, en de Fransen d'Alembert en Lagrange de mechanica in de achttiende eeuw verder ontwikkeld tot op de aanzienlijke hoogte waarop Lagrange zelf in zijn Mécanique analytique van 1788 de ontwikkeling aan het eind der eeuw weer afsluit.

Gaan wij thans over tot het tweede gezichtspunt dat men aan de beschouwing van Descartes ontlenen kan, dat der axiomatisering, dan moet vooreerst worden bedacht dat het woord axiomatisering in een dubbele betekenis kan

[p. 145]

worden opgevat; men kan een gebied axiomatiseren in die zin dat men een reeds aanwezig systeem van oordelen logisch ordent, door te onderzoeken uit welke onbewezen grondstellingen al die oordelen kunnen worden gededuceerd; maar ook zo dat men een of andere uitspraak om haar grote evidentie of op empirische gronden zonder bewijs aanvaardt en nu nagaat welke conclusies men daaruit in verbinding met andere reeds bekende stellingen kan trekken. Van beide vormen, die men als axiomatica a posteriori en axiomatica a priori kan onderscheiden, levert de mechanica der zeventiende en achttiende eeuw duidelijke voorbeelden. Ik noem in de eerste plaats de behandeling van het verschijnsel van de vrije val. Galilei had hierbij a priori aangenomen dat de snelheid van een vallend lichaam in onderling gelijke tijden met onderling gelijke bedragen toeneemt, en daaruit met behulp van de grafische methode al de kinematische eigenschappen der valbeweging afgeleid. Het probleem was nu verder axiomata van dynamische aard te vinden, die in staat zouden stellen deze resultaten te deduceren uit de steeds aan de hele beschouwing ten grondslag liggende overtuiging dat de val veroorzaakt wordt door de zwaarte van het lichaam en dat die zwaarte tijdens de val constant blijft. Voor de peripatetische fysica was het namelijk altijd een onoplosbaar raadsel gebleven hoe het mogelijk is dat een constante bewegingsoorzaak een versnelde beweging kan opleveren. De pogingen nu tot dynamische axiomatisering van de kinematica der valbeweging hebben in een langdurige ontwikkeling, waarop ik hier niet kan ingaan, geleid tot de opstelling van de eerste twee Axiomata sive Leges Motus, die Newton aan het eerste boek van zijn Principia laat voorafgaan, de traagheidswet en de wet van de evenredigheid van de kracht en de fluxie van de impuls of de hoeveelheid beweging, welke laatste grootheid wordt bepaald als produkt van de massa van het lichaam en zijn momentane snelheid. Van die axiomata had het eerste nog verschillende andere wortels dan het inzicht dat men de versnelling van de valbeweging kon verklaren door de aanname dat de zwaarte in gelijke tijdsdelen gelijke snelheden voegt bij de reeds vroeger voortgebrachte, waarvan men onderstelt dat ze behoudens uitwendige oorzaken van verandering blijven voortbestaan. Galilei had namelijk reeds op tal van empirische gronden het voorkomen van de eigenschap der traagheid, die een van zijn voornaamste wapenen was in zijn weerlegging van de peripatetische bezwaren tegen de leer der bewegende aarde, betoogd en ook verder blijken bij de definitieve formulering der traagheidswet de argumenten die de empirie rechtstreeks aan de hand deed en die aan de axiomatische bruikbaarheid, dus indirect ook aan de aansluiting aan de empirie, waren ontleend, elkaar voortdurend te ondersteunen. Het krachtbegrip van Newton echter dankt zijn ontstaan wel geheel aan de pogingen om voor de leer van de vrije val de grondslagen te vinden waaruit de reeds bekende kinematische stellingen deductief konden worden afgeleid; het is in zijn scherp contrast tot het gelijknamige begrip in de peripatetische natuurbeschouwing een van de duidelijkste voorbeelden van de begripsvormende werking der axiomatische

[p. 146]

methode. Een tweede niet minder duidelijk voorbeeld vindt men in het gravitatie-axioma van Newton, dat tot opbouw van zijn wereldsysteem dient; ook hieraan ligt het streven ten grondslag een algemene basis te vinden waaruit de verschijnselen van val en worp op aarde en van de planetenbeweging aan de hemel met behulp van de algemene mechanische axiomata zouden kunnen worden gededuceerd. Het is waar dat Newton zelf zijn denkwijze bij de invoering van de gravitatietheorie als inductie betitelt, maar inductie en axiomatica a posteriori zijn dan ook zeer nauw verwant; het zijn twee aspecten van hetzelfde proces, namelijk het opsporen van de onbekende grond van een gegeven verschijnsel; men noemt het inductie wanneer men die grond beschouwt als de fysische causa, axiomatica, wanneer men haar ziet als de logische ratio, of om met Newton te spreken, als de causa mathematica.

Van de axiomata a priori, die om hun evidentie uitgangspunt van redenering worden en waaruit dan stellingen worden afgeleid die men nog niet kende, zijn in de zeventiende eeuw niet minder treffende voorbeelden te vinden. Ik noemde al even het axioma van de onmogelijkheid van het perpetuum mobile, waaruit Stevin de wet van het hellend vlak en de wet van Archimedes afleidt; een tweede is het axioma van Huygens, dat voor het homogeen gedachte zwaarteveld der aarde equivalent is met de wet van behoud van mechanisch arbeidsvermogen. Huygens kwam tot dit axioma door generalisering van een statisch axioma van aristotelisch-scholastische oorsprong, dat in de vijftiende en zestiende eeuw door de Italiaanse mechanica was toegepast en dat door Torricelli in 1644 uitdrukkelijk was geformuleerd. Het luidt bij Torricelli aldus dat een stelsel van zware lichamen die onderling verbonden zijn, niet uit zichzelf in beweging kan komen, wanneer niet hun gemeenschappelijk zwaartepunt daalt. Huygens heeft nu vooreerst van dit zelfde axioma nieuwe toepassingen gemaakt door het als grondslag te gebruiken voor de theorie van het evenwicht van een zwaar koord en van zijn hydrostatische onderzoekingen. Bovendien heeft hij het echter dynamisch gegeneraliseerd door het toe te passen op een systeem van lichamen in beweging, waarbij hij op een gegeven ogenblik onder de zwaartepuntshoogte van het systeem, die niet zonder uitwendige oorzaken kan toenemen, de hoogte verstaat waarop het zwaartepunt zich zou bevinden indien alle lichamen de snelheden die zij op dat ogenblik hebben, gebruikten voor een verticale stijgbeweging en wanneer zij dan in het hoogste bereikte punt werden vastgehouden. Met behulp van dit axioma werd dan bij hem de botsingstheorie ontwikkeld. Als derde voorbeeld van een axioma van de nu behandelde soort noem ik nog het zogenaamde relativiteitsaxioma der klassieke mechanica, waarin wordt uitgesproken dat alle mechanische verschijnselen in een stelsel van lichamen onveranderd blijven wanneer men aan het gehele systeem een eenparige rechtlijnige translatie geeft ten opzichte van het beschrijvingsraam waarin men de mechanische wetten had afgeleid. Van dit axioma heeft weer vooral Huygens, ook weer in de botsingstheorie, een vernuftig gebruik gemaakt.

[p. 147]

Ik zal mij tot de genoemde voorbeelden beperken en vermeld dus slechts even terloops de axiomatisering der statica bij Stevin en Varignon en dat meesterstuk van logische ordening van een reeds in hoofdtrekken bekend systeem van stellingen dat Blaise Pascal voor de hydrostatica verricht in zijn Traité de l'équilibre des liqueurs.

Ik neem nu aan dat door het bovenstaande aannemelijk zal zijn gemaakt dat de toepassing der wiskunde een belangrijk hulpmiddel is geweest in de beoefening van de mechanica der zeventiende eeuw. Mag men hieruit - zo zou men kunnen vragen - nu echter ook besluiten dat de opbloei die juist deze wetenschap in die tijd vertoont, geheel of althans in hoofdzaak aan haar mathematisering is toe te schrijven? Bestaat niet de mogelijkheid dat een belangrijk deel van de bereikte vooruitgang op rekening van andere factoren moet worden gesteld en dat de intrede der mathesis geen andere dan secundaire en formele betekenis heeft gehad? Als men die vraag zo stelt - en het is niet zelden gebeurd - dan denkt men natuurlijk in de eerste plaats aan de nieuwe kenbron die het zeventiende-eeuwse denken over de natuur in de empirie en het experiment had verworven en men bedoelt er meestal reeds de bewering mee dat in het intense gebruik van deze kenbron de ware oorzaak van de waargenomen bloei te zoeken is. Nu leert echter de studie van de werken der grote mechanici der zeventiende eeuw dat empirie en experiment, hoe hoogst belangrijk ook in het algemeen hun invloed op de natuurwetenschap van die tijd zijn geweest, in de ontwikkeling der mechanica toch ongetwijfeld niet die grote betekenis hebben gehad die het dogmatisch empirisme der negentiende eeuw er wel graag op dit gebied aan heeft willen toedichten.^*

Er wordt natuurlijk wel geëxperimenteerd in de mechanica, maar het geschiedt vrijwel uitsluitend ter verificatie van mathematisch afgeleide wetten, dus niet met heuristische bedoelingen. Galilei controleert met valproeven op een hellend vlak de langs deductieve weg gevonden afhankelijkheid van afgelegde weg en verstreken tijd in val uit rust; met slingerproeven demonstreert hij achteraf de betrouwbaarheid van het als basis van de theorie van het hellend vlak gekozen axioma dat de in val uit rust over zekere verticale afstand verworven snelheid onafhankelijk is van de hellingshoek. Dat de relatie van theorie en experiment bij deze onderwerpen in werkelijkheid een andere zou zijn geweest dan in de definitieve uiteenzetting, dat hij de valwet uit waarnemingen zou hebben afgeleid en het postulaat der gelijke eindsnelheden inductief uit slingerproeven zou hebben gevonden, is vaak beweerd maar nooit aannemelijk gemaakt, laat staan bewezen. Er worden verder enkele toestellen ontworpen om de vrije val te kunnen bestuderen, maar ook zonder de voltooiing daarvan wint de overtuiging van de juistheid van Galilei's theorie onweerstaanbaar veld. De proeven over vrije val die Riccioli vanaf de toren te Bologna doet, zijn interessant voor de geschiedenis van de meettechniek, maar invloed op de historische ontwikkeling der mechanica hebben ze nauwelijks gehad en de al te schone overeenstemming van hun resultaten met de te

* De stelling dat de wetenschappelijke revolutie van de zeventiende eeuw niet gekenmerkt wordt door de invoering van de empirische methode, maar vooral door strikt conceptuele veranderingen in natuurwetenschappelijk denken (in het bijzonder in de mechanica) zou later grote bekendheid verwerven door de publikaties van de Franse filosoof en wetenschapshistoricus Alexandre Koyré, vooral diens Etudes galiléennes (Parijs, 1939).

[p. 148]

verifiëren valwet maakt ze verdacht. In de hydrostatica ontmoet men dezelfde situatie. Stevin bouwt zijn theorieën streng mathematisch op en eerst in een aanhangsel van zijn werk beschrijft hij een toestel ter demonstratie van de hydrostatische paradox. Pascal vermeldt wel allerlei experimenten met lange glasbuizen, die hij te Rouen zegt te hebben gedaan, maar als Boyle in zijn Hydrostatical paradoxes die proeven behandelt, moet hij meer dan eens opmerken dat niet iedere proef die een mathematicus kan verzinnen ook door een fysicus kan worden uitgevoerd, en men krijgt inderdaad de indruk dat Pascal bij het schrijven van zijn Traité niet steeds nauwgezet onderscheid heeft gemaakt tussen werkelijk uitgevoerde en slechts in gedachten verrichte experimenten. Het belangrijkst voor de ontwikkeling der mechanica zijn waarschijnlijk nog de proeven over slingerbeweging geweest, waaruit Galilei al te veel heeft willen afleiden (namelijk isochronisme voor alle amplitudines), die Huygens hebben geïnspireerd tot zijn prachtige theorieën over de fysische slinger en tot zijn ontdekking van het tautochronisme van de cycloïdale valbeweging en die bij Newton worden gebruikt om de evenredigheid van trage en zware massa aan te tonen.

Door deze enkele opmerkingen is het vraagstuk van de relatie tussen wiskunde en empirie in de ontwikkeling der mechanica niet uitgeput; ze zijn echter wel toereikend om de nog veel voorkomende overschatting van de betekenis die in de ontwikkeling van de zeventiende-eeuwse mechanica aan de empirie als kenbron moet worden gehecht, in het licht te stellen en daardoor de ogen voor de machtige invloed van de mathematisering der mechanische theorieën te helpen openen. Of de opvattingen die de grote grondleggers van deze theorieën over de onderlinge betrekkingen tussen mathematische deductie en empirische inductie hadden, volgens de zienswijzen van onze tijd meer of minder juist zijn, doet daarbij niet ter zake. Het is een historisch feit dat zij over het algemeen een sterke neiging hebben de mechanica geheel als onderdeel der wiskunde te beschouwen, haar axiomata op een lijn te stellen met die der wiskunde en zich over de aansluiting aan de ervaring, die wegens de verwaarlozing van alle storende invloeden als wrijving en luchtweerstand, toch altijd zeer onvolkomen is, evenmin zorgen te maken als de meetkundigen dat doen over de overeenstemming van hun stellingen met de resultaten van metingen aan fysische lichamen. In de achttiende eeuw wordt die neiging door schrijvers als Euler en d'Alembert zelfs zozeer op de spits gedreven dat men gerust van een inlijving van de mechanica bij de wiskunde spreken kan.

Over het waarheidsgehalte van die opvatting kan men, kennistheoretisch redenerend, van mening verschillen; over haar vruchtbaarheid in de historische ontwikkeling nauwelijks. Alle lectuur van de grote schrijvers over mechanica die de zeventiende en de achttiende eeuw hebben voortgebracht, wekt de overtuiging dat zij hun wetenschap groot hebben kunnen maken omdat zij het inzicht hebben bezeten in de dubbele functie die de wiskunde in de natuurwetenschap heeft te vervullen, die van taal en die van instrument. Zij

[p. 149]

hebben begrepen dat noch de gewone omgangstaal, noch de kunsttaal der filosofie fijn genoeg waren gebouwd om de complicatie der natuurverschijnselen te beschrijven en het infinitesimale karakter van de fundamentele natuurwetenschappelijke begrippen tot zijn recht te doen komen. Als hun aller zinspreuk zouden de befaamde woorden kunnen gelden die Galilei in Il saggiatore heeft gesproken: ‘De wetenschap staat geschreven in het grote boek dat ons voortdurend open voor ogen ligt (ik bedoel het heelal), maar zij kan niet begrepen worden indien men niet eerst de taal leert verstaan, en de letters leert kennen waarin zij staat uitgedrukt. Zij is geschreven in mathematische taal en de letters zijn driehoeken, cirkels en andere geometrische figuren, zonder welke middelen het onmogelijk is haar woorden op menselijke wijze te verstaan en zonder welke men niets anders kan doen dan doelloos ronddwalen in een duister labyrint.’ Het is het oude motief van de pythagoreïsch-platonische filosofie dat hier opnieuw weerklinkt: de dingen zijn getallen en God gaat steeds geometrisch te werk. Wat echter in de Griekse natuurwetenschap in hoofdzaak programma was gebleven, werd in de zeventiende-eeuwse mechanica werkelijkheid; zij heeft zozeer partij weten te trekken van de nieuwe methoden die de wiskunde had geschapen, dat zij een blijvend fundament kon worden voor de vruchtbare beoefening van de natuurwetenschap.

II

Het jaar 1687, waarin Newtons Principia verschenen, vormt in zekere zin het eindpunt van de ontwikkeling der zeventiende-eeuwse mechanica omdat in dat werk èn de algemene axiomata worden geformuleerd waaruit de wetten der beweging zijn te deduceren èn het bijzondere gravitatie-axioma dat de toepassing van die wetten op de val en de planetenbeweging mogelijk maakt, terwijl het tevens de uiteenzetting van het wiskundig hulpmiddel voor de beoefening der mechanica bevat dat in de infinitesimaalrekening was gevonden. Het zou nu kunnen lijken alsof daarmee de geschiedenis der klassieke mechanica in beginsel beëindigd was. We moeten er echter voorzichtig mee zijn om een oordeel dat wij tegenwoordig op grond van onze inzichten in de intrinsieke betekenis van een werk uitspreken, nu ook maar dadelijk te formuleren als een historische uitspraak over de wijze waarop dat werk in zijn tijd werd gezien en over de waarde die er toen aan werd toegekend. Dat zulk een overdracht van beoordeling onjuist kan zijn en dus steeds ongeoorloofd is, blijkt wel heel duidelijk juist aan het voorbeeld van Newtons werk, dat door meer dan één oorzaak een veel minder diepe indruk op zijn tijdgenoten heeft gemaakt dan wij thans op grond van zijn wetenschappelijke betekenis menen te mogen verwachten.

In de eerste plaats wordt Newtons afleiding van val en planeten beweging uit

[p. 150]

het gravitatie-axioma in de eerste tientallen jaren na de publikatie door de meest competente beoordeelaars op het vasteland vrijwel eenstemmig verworpen. Dat is eigenlijk heel begrijpelijk wanneer men bedenkt dat omstreeks 1700 de cartesiaanse wijze van natuurbeschouwing, hoewel in haar concrete uitwerking reeds door velen veroordeeld, in beginsel nog de heersende is, terwijl daarnaast het klassieke atomisme van Democritus en Epicurus in zijn onder andere door Gassend vernieuwde vorm veld wint. Deze twee denkrichtingen, waarvan de eerste de materie ziet als continu in de ruimte uitgespreid of zelfs als identiek daarmee, terwijl de tweede een discontinue materieverdeling in een overigens lege ruimte aanneemt, hebben in die tijd het gemeenschappelijk kenmerk dat zij alle verschijnselen terugbrengen tot de inwerking op elkaar van aangrenzende delen der materie, hetzij dat aangrenzend zijn doorlopend is als in de theorie van Descartes, of momentaan zoals bij de botsingen der atomen. In geen van beide is daardoor plaats voor een werking op afstand, zoals Newton die scheen te postuleren om de val en de planetenbeweging te verklaren. Vandaar dan ook dat zijn gravitatietheorie èn door Huygens èn door Leibniz en door Johan Bernoulli, om drie van de grootsten van hun tijd te noemen, volstrekt wordt verworpen. Zo schrijft bijvoorbeeld Leibniz in 1690 aan Huygens, na waarderende woorden aan Newtons boek te hebben gewijd: ‘Cependant je ne comprends pas comment-il conçoit la pesanteur ou attraction. Il semble que selon luy ce n'est qu'une certaine vertu incorporelle et inexplicable, au lieu que vous l'expliqués tres plausiblement par les loix de la mécanique’;^* en Huygens zegt in zijn antwoord kortweg dat het attractieprincipe hem absurd lijkt. Er is een algemeen streven om de zwaarte te verklaren met behulp van een hypothetische ether, zoals Huygens dat in zijn Discours de la cause de la pesanteur had gedaan en de methode van Newton, die later als het ideale voorbeeld van een mechanische natuurtheorie zou gelden, kon blijkens de woorden van Leibniz in die tijd nog om haar niet-mechanisch karakter worden veroordeeld.

Er is nog een andere reden die tot dit gemis aan waardering kon bijdragen. Men moet namelijk steeds bedenken dat de zeventiende-eeuwse natuurwetenschap zich heeft ontwikkeld in scherpe en bewuste oppositie tot de methode van natuuronderzoek der peripatetische filosofie en er is dan ook niets wat aan haar beoefenaren zo verwerpelijk voorkomt als een terugvallen in de denkwijze en de terminologie van een standpunt dat men voorgoed meende te hebben overwonnen. Maar moest het nu niet de schijn hebben dat in de attractie-theorie van Newton de beruchte qualitates occultae der scholastiek, waarmee alle natuurverschijnselen maar al te gemakkelijk waren verklaard, in volle kracht herleefden? Men denke bijvoorbeeld aan de beroemde passage uit Le malade imaginaire, waarin Molière, die met Gassend bevriend was en die dus de anti-scholastische stemming der nieuwe natuurwetenschap van nabij moet hebben gekend, de traditionele wetenschap bespot doordat hij aan een baccalaureus de vraag laat stellen waarom opium doet slapen, waarop deze

* ‘cependant’: ‘Toch begrijp ik niet hoe hij de zwaarte of de aantrekking opvat, het schijnt dat het volgens hem slechts een zekere onstoffelijke en onverklaarbare kracht is, terwijl u haar zeer plausibel verklaart door middel van de wetten van de mechanica.’

[p. 151]

triomfantelijk en met lof van het koor het antwoord geeft: ‘Quia est in eo virtus dormitiva, cujus est natura sensus assoupire.’^* Zou de sarcastische bedoeling van deze passage voor de tijdgenoten niet even goed bereikt zijn wanneer de vraag had geluid waarom zware lichamen naar de aarde toevallen en wanneer de kandidaat daarop met een anticipatie van Newtons theorie had geantwoord: Quia est in ea virtus attractiva, cujus est natura gravia movere.’^* Zo ziet Leibniz het blijkbaar wanneer hij van een vertu incorporelle et inexplicable spreekt en al de kritiek op Newton die men tot in het midden van de achttiende eeuw ontmoet, past in deze zelfde gedachtengang.

Wanneer men nu echter meer let op wat Newton zelf met zijn theorie heeft bedoeld dan op wat sommigen van zijn volgelingen ervan hebben gemaakt, blijkt deze kritiek wel geheel op misverstand te berusten. Ze zou gerechtvaardigd zijn wanneer Newton hypothetisch de gravitatie als een aan de materie inherente kwaliteit had ingevoerd en daarmee val en planetenbeweging verklaard had geacht. Kwaliteiten zijn nu eenmaal occult en men kan ze niet anders manifest maken dan òf door samenvatting onder één gezichtspunt van wat schijnbaar verschillend van aard is òf door mathematische omschrijving en bepaling. En nu kan men ten eerste volhouden dat Newton zowel het ene als het andere heeft gedaan door de grootte der gravitatiewerking vast te leggen in een kwantitatief geformuleerde wet en door de identiteit van de kracht die de maan in haar baan houdt en die de steen naar de aarde doet vallen, door berekening aan te tonen. Maar ten tweede kan men zijn gedachtengang nog beter benaderen en hem daardoor nog effectiever tegen de kritiek van zijn grote tijdgenoten verdedigen, door te zeggen dat de gravitatie voor hem helemaal geen kwaliteit der materie is en haar bestaan geen hypothese. Dat op een planeet een kracht werkt die gericht is naar de zon en omgekeerd evenredig met het vierkant van de afstand tot de zon, is een mathematische consequentie uit de wetten van Kepler in verband met de algemene axiomata der mechanica; het woord kracht, dat altijd de illusie van een oorzaak wekt, is daarbij niets anders dan een volkomen ontbeerlijke afkortende uitdrukking voor het produkt van de massa en de versnelling. Het gravitatie-axioma geeft van de verschijnselen van val en planetenbeweging noch een fysische, noch een metafysische verklaring, maar uitsluitend een mathematische beschrijving. Een verklaring tracht Newton in de Principia voor de gravitatie evenmin te geven als Galilei het in de Discorsi voor de wetten van de vrije val had trachten te doen. De passage, waaraan het beroemde woord ‘Hypotheses non fingo’ ontleend is, spreekt het met de grootste nadruk uit dat verklaringshypothesen, van welke aard ook, in de philosophia experimentalis of naturalis niet thuishoren.

In deze strenge beperking tot beschrijving in mathematische termen van de langs empirische weg verkregen kennis der natuurverschijnselen, in deze afwijzing van iedere pretentie tot het doordringen in het wezen der verschijnselen door hypothetische verklaringen, komt een kennistheoretische

* ‘Quia est in eo virtus dormativa’: ‘Omdat daarin een slaapverwekkende kracht huist, waarvan het de aard is de zintuigen te verdoven.’

* ‘Quia est in ea virtus attractiva’: ‘Omdat daar een aantrekkende kracht in huist, waarvan het de aard is zware lichamen in beweging te brengen.’

[p. 152]

visie op het doel en de draagwijdte der natuurwetenschappelijke methode tot uiting die in veel nauwer verband staat met de opvattingen die er op dit punt in onze eigen tijd bestaan, dan met de minder geresigneerde denkbeelden die er in de negentiende eeuw over in omloop zijn geweest. Het hangt daarmee samen dat de waardering voor Newtons werk tegenwoordig weer een aanmerkelijke stijging vertoont en dat er weer een nieuwe fase schijnt te zijn ingetreden in de merkwaardige wisselingen die zijn historisch beeld in de loop der tijden reeds heeft ondergaan.^* Die wisselingen zijn reeds in de achttiende eeuw duidelijk waar te nemen; in dezelfde tijd waarin Huygens, Leibniz en Bernoulli nog zonder juist begrip tegenover de Principia staan, vinden Newtons denkbeelden in Engeland reeds warme instemming, zij het dan ook niet steeds op zuiver wetenschappelijke gronden; die instemming breidt zich in de loop van de achttiende eeuw wel uit tot het continent, maar ze gaat dan gepaard met een interpretatie van de gravitatietheorie die geheel tegen de bedoelingen van haar schepper indruist.

Het is namelijk wel waar dat Newton zich in de Principia streng heeft beperkt tot het ontwikkelen van een mathematische theorie der bewegingsverschijnselen, maar we weten uit de Optica, uit zijn brieven en uit de uitlatingen van zijn vroegste en door hem zelf geautoriseerde interpretatoren, zoals Cotes, Bentley en Clarke, ook nog wel het een en ander omtrent de motieven die hem tot de strikte beperking van zijn onderzoek hebben gevoerd en over de verwachtingen die hij aangaande de uitwerking van zijn geschriften koesterde. En wel wordt men langs deze weg, waarvan het bewandelen onmisbaar is wanneer men een volledige kijk op Newtons persoonlijkheid wil verkrijgen, voornamelijk gewaar in welk een sterk theïstisch gestemde sfeer de gehele gravitatietheorie is geconcipieerd en uitgewerkt. Newton heeft zich uitvoerig bezig gehouden met het vinden van een dieperliggende verklaring der gravitatie, waarover hij twee verschillende theorieën heeft ontwikkeld, waarvan de ene in nauw verband staat met zijn theologische overtuigingen. Deze bewering schijnt wellicht in tegenspraak met de boven geciteerde woorden, dat verklaringshypothesen, van welke aard ook, in de philosophia naturalis niet thuishoren; die tegenspraak bestaat echter niet; men moet in die woorden de nadruk leggen op philosophia naturalis, een uitdrukking die gelijkwaardig is met wat wij natuurwetenschap noemen; daarin passen inderdaad geen andere theorieën dan die door axiomatisering of algoritmisering van de resultaten der empirie zijn verkregen; maar dat sluit niet uit dat men in de philosophia generalis, die voor Newton wel ongeveer met de theologie samenvalt, wel kan trachten de resultaten van het natuuronderzoek in te passen in het algemene wereldbeeld der geopenbaarde christelijke religie. Dat heeft Newton inderdaad beproefd en zo is hij, onder invloed van Jacob Boehme, wiens werken hij intens heeft bestudeerd, en van de Engelse neo-platoonse theoloog Henry More, gekomen tot zijn theorie van het immateriële actieve principe dat de op zichzelf inerte materie beweegt volgens de bedoelingen

* ‘Newtons werk’: Een blijk van de nieuwe aandacht voor Newton was de publikatie van een Nederlandse studie van zijn Principia: H.J.E. Beth, Newtons Principia (2 delen, Groningen, 1932). Beth was een goede vriend van Dijksterhuis en het boek verscheen in de door Beth en Dijksterhuis geredigeerde serie Historische bibliotheek voor de Exacte Wetenschappen.

[p. 153]

van de Schepper, welke in de mathematische gravitatiewet worden uitgedrukt.

Empirisch kan het nu de schijn hebben alsof een lichaam een werking op afstand op een ander lichaam uitoefent. Echter Newton verwerpt het denkbeeld dat die actio in distans een fysische realiteit zou beduiden, dat de gravitatie een attribuut der materie zou zijn, waardoor het lichaam zou kunnen werken waar het niet is, met de meeste nadruk; er moet een intermediair agens zijn waaruit de schijnbare werking op afstand voortvloeit en dat, zelf onstoffelijk, door het medium van de absolute ruimte, die het eindeloze sensorium Gods is, de materie beweegt. Zo beschouwd kon de gravitatie-theorie in Newtons eigen ogen een direct bewijs worden voor het bestaan van God in de theïstische zin van het woord; en hij heeft zelf uitdrukkelijk verklaard dat niets hem meer zou verheugen dan wanneer zijn Principia op deze wijze zouden kunnen bijdragen tot de bestrijding van het atheïsme.

Vergelijkt men de manier waarop de gravitatietheorie in de achttiende eeuw in Frankrijk is toegepast met Newtons uitgesproken bedoelingen aangaande haar psychologische uitwerking, dan blijkt dat, naarmate de theorie zelf grotere triomfen viert, van die bedoelingen minder terecht komt. Met de verdoezeling van het onderscheid tussen de causa mathematica van een verschijnsel en de causa physica, dat Newton zo zorgvuldig in acht neemt, kreeg de werking op afstand steeds meer het karakter van een fysische inwerking van twee lichamen op elkaar, werd de gravitatie steeds meer als inherent aan de materie beschouwd, en werd het streng-mathematische wereldsysteem van de Principia steeds meer los gemaakt uit het theïstische verband waarin het oorspronkelijk was geplaatst. ‘Ce système, qui soulage si fort la Providence’,^* zoals Montesquieu zegt, scheen ‘la Providence’ langzamerhand overbodig te maken. En men kan nauwelijks een meer treffend voorbeeld vinden van het contrast dat er vaak tussen Newtons bedoelingen en de uitwerking van zijn denkbeelden heeft bestaan, dan door de theologische beschouwingen van hem en zijn vrienden inzake de gravitatie als existentiebewijs Gods te vergelijken met het befaamde antwoord dat Laplace aan Napoleon gaf, toen deze hem vroeg waarom hij in zijn Mécanique céleste nergens de Schepper had vermeld: ‘Sire, je n'avais pas besoin de cette hypothèse-là.’^*

Als tweede voorbeeld van verschil in waardering van Newtons werk in zijn eigen tijd en later kan de fundering der mechanica in de drie Axiomata sive Leges Motus gelden, die aan het eerste boek der Principia voorafgaan. Het blijkt namelijk dat deze fundering kort na het verschijnen van het werk lang niet zozeer als definitief werd beschouwd als wij ons dat thans onwillekeurig voorstellen. Men krijgt zelfs wel eens de indruk dat men er aanvankelijk zelfs maar heel weinig aandacht aan heeft geschonken. Wanneer Johan Bernoulli en Leibniz in de laatste jaren der eeuw uitvoerig corresponderen over fundamentele vragen der mechanica, noemen ze Newton nauwelijks; tot midden in de achttiende eeuw worden, geheel onafhankelijk van de axiomatische grondslag

* ‘Ce système’: ‘Dat systeem, dat zozeer de Voorzienigheid ontlast’.

* ‘Sire’: ‘Sire, ik had geen behoefte aan die hypothese’.

[p. 154]

die in de Principia gelegd was, zelfstandige mechanische principes axiomatisch aanvaard en de grote discussies over de mechanica gaan voor een groot deel geheel buiten Newton en zijn werk om. Er bestaat namelijk naast de ontwikkelingslijn der mechanica die we tot dusver hoofdzakelijk hebben beschouwd, en die door de namen Galilei, Huygens, Newton kan worden gekenmerkt, een andere, die in grote trekken te typeren is door de namen Descartes, Leibniz, Bernoulli en misschien Maupertuis. Een van haar voornaamste kenmerken is dat zij in veel nauwer verband staat met filosofische en religieuze opvattingen van haar scheppers dan dat bij de eerstgenoemde schrijvers het geval was. Bij dezen bestond natuurlijk, zoals we al zagen, ook wel verband tussen filosofie of godsdienst aan de ene kant en de stijl van natuuronderzoek aan de andere, maar dat verband bepaalde uitsluitend de achtergrond waarop zich hun werk afspeelt; metafysische argumenten werden niet in de opbouw van de systemen gebruikt (men kan bijvoorbeeld de Principia met uitzondering van het laatste Scholium lezen zonder iets van de theologische overtuigingen van Newton te vermoeden) en ze zijn dus meer psychologisch belangrijk voor de kennis van de persoonlijkheid van de schrijvers dan essentieel voor de logische samenhang van hun systemen.

Geheel anders is dit bij filosofen als Descartes en Leibniz. Bij hen wordt de opbouw der mechanica onmiddellijk in verband gebracht met, ja afgeleid uit het metafysische stelsel en men kan hun mechanische redeneringen in het geheel niet volgen zonder van hun metafysica kennis te nemen. Ik wil trachten van die noodzaak een indruk te geven door iets mee te delen over de grote strijd tussen de cartesianen enerzijds en Leibniz met zijn aanhangers anderzijds over het wezen der materie en de maat van de zogenaamde kracht.

Descartes, die de subjectiviteit verkondigde van de zogenaamde secundaire kwaliteiten der materie, zoals kleur, smaak, hardheid en gewicht, heeft des te krachtiger vastgehouden aan de objectiviteit van de geometrisch-mechanische primaire kwaliteiten grootte, vorm en beweging. Dat hij dit deed is op grond van zijn algemene denkbeginselen volkomen begrijpelijk. Wáár toch is, volgens de eerste regel van het denken in het Discours de la méthode, alles waarvan wij ‘des idées claires et distinctes’ hebben; zulke denkbeelden had hij echter van de fundamentele inzichten van wiskunde en kinematica in hoge mate en de schepping van een geometrisch-mechanisch wereldbeeld blijkt feitelijk bij hem de directe consequentie te zijn van de typisch-mathematische geestesgesteldheid waardoor hij zelf een onuitwisbare stempel op het natuurwetenschappelijk denken van de zeventiende eeuw heeft gedrukt. In overeenstemming met de aanvaarding van grootte, vorm en beweging als objectieve kwaliteiten ziet Descartes het wezen der materiële substantie in de driedimensionale uitgebreidheid en daarin alleen. Wat het is dat zich in drie dimensies uitstrekt, zegt hij niet. Hij heeft, zoals Huygens het uitdrukt, van de materie de voorstelling die anderen van het vacuüm hebben. Voor Descartes zelf bestaat natuurlijk het vacuüm niet; waar ruimte is, is materie. De materie nu is in

[p. 155]

de aanvang geschapen in rust en beweging, van welke modi God dus de primaire oorzaak is. Uit de onveranderlijkheid Gods leidt Descartes nu het diepstliggend axioma van zijn mechanica af: de totale hoeveelheid beweging in het heelal, dat is dus de som van de produkten van iedere hoeveelheid materie en haar snelheid, kan niet veranderen. Uit dezelfde metafysische overweging volgen nu ook de bijzondere bewegingswetten, die de secundaire en particuliere oorzaken zijn van de bewegingen die we in de lichamen opmerken. Ten eerste de wet dat ieder lichaam behoudens inwerking van uitwendige oorzaken, vorm en bewegingstoestand, dat wil zeggen grootte en richting der snelheid, behoudt. En vervolgens dat bij de botsing van twee lichamen de totale hoeveelheid beweging behouden blijft. Schijnbaar wordt dus in deze wetten aangenomen dat in de materie de eigenschap der traagheid zetelt, die als streven naar behoud van impuls kan worden omschreven, en dat twee lichamen bij een botsing krachten op elkaar uitoefenen die de wederzijdse impulsen met behoud van hun som wijzigen. In werkelijkheid is voor het consequente cartesianisme noch het een noch het ander het geval. De materie volhardt in haar bewegingstoestand niet op grond van een inwendig vermogen, dat zich uit als weerstand tegen uitwendige pogingen om de grootte of de richting der snelheid te wijzigen, maar omdat God op ieder ogenblik haar momentane impuls in stand houdt. En, metafysisch beschouwd, werkt een lichaam niet op een ander in wanneer het ertegen botst, maar God regelt bij de ontmoeting de impulsen van beide zo dat de som niet verandert. De materie zelf is zuiver passief, in overeenstemming met haar geometrische essentie. Empirisch echter vertoont ze natuurlijk de schijn van activiteit; een bewegend lichaam oefent, fenomenologisch gesproken, werkingen op andere, mits kleinere lichamen uit die het in een botsing ontmoet; het kan de weerstand van een medium gedurende enige tijd overwinnen. Als maat voor het vermogen zulke werkingen uit te oefenen, dient nu ook hetzelfde produkt van massa en snelheid; de cartesianen noemen het force motrice van het lichaam, waarbij blijkbaar deze ‘kracht’ identiek is met wat wij de impuls noemen en toto genere verschillend van kracht in de zin van Newton, die met de fluxie, de veranderingssnelheid, van de impuls evenredig is.

Tegen deze theorie van zijn grote voorganger in de filosofie is nu Leibniz onophoudelijk met al de kracht van zijn argumentatie opgekomen. Telkens weer betoogt hij de ongerijmdheid van het denkbeeld het wezen der materie in de uitgebreidheid te zoeken en de totale hoeveelheid beweging te zien als het voor ieder afgesloten systeem onveranderlijke quantum, dat ook hij in de wisseling der bewegingsverschijnselen wil vinden. En zozeer gaat het onderwerp hem ter harte dat men al spoedig de indruk krijgt dat het niet zuiver interne aangelegenheden der theoretische mechanica zijn die hem aansporen tot zo heftig verzet. Dat die indruk juist is, bevestigt hij zelf in zijn briefwisseling met Antoine Arnauld, de theoloog en mathematicus van Port-Royal. Het blijkt hier dat althans een van de wortels van zijn eigen opvatting

[p. 156]

over het wezen der materie en de maat van de kracht van een bewegend lichaam geheel op religieus gebied ligt. Leibniz heeft zich namelijk lange tijd ernstig beijverd een weg te vinden waarlangs katholieken en protestanten weer tot vereniging in één kerk konden worden gebracht en hij heeft daarbij geprobeerd de bezwaren die van protestantse zijde tegen het dogma der transsubstantiatie werden aangevoerd, te weerleggen en in het algemeen de logische tegenstrijdigheden op te heffen die de menselijke rede in het mysterie der eucharistie kon ontdekken.

Het dogma der transsubstantiatie, zoals het door het concilie van Trente in 1551 was vastgesteld, leert dat na de consecratie de substantie van het brood en de wijn met behoud van de accidentia, dus der uitwendige verschijningsvormen, veranderd zijn in de substantie van het lichaam en het bloed van Christus en dat Christus dus, hoewel volgens zijn natuurlijke wijze van bestaan voortdurend gezeten ad dexteram patris,^* niettemin vere, realiter ac substantialiter^* aanwezig is onder de vorm van de zintuigelijk waarneembare stoffen brood en wijn. Tegen dit dogma kon de menselijke rede in hoofdzaak drie bezwaren aanvoeren; er kon ten eerste gevraagd worden hoe de substanties van brood en wijn kunnen veranderen in andere substanties die slechts ad modum spiritus^* aanwezig zijn; ten tweede, hoe het mogelijk is dat Christus gelijktijdig aanwezig is in de hemel en op alle altaren der aarde waarop de consecratie wordt verricht; en ten slotte, hoe de accidentia van brood en wijn kunnen blijven voortbestaan zonder een substantie, die hun drager is. Het is nu duidelijk dat deze drie moeilijkheden met de materietheorie van Descartes niet zijn op te lossen. Immers, als uitgebreidheid identiek is met de lichamelijke substantie, is een bestaan van het lichaam en het bloed van Christus ad modum spiritus ongerijmd, is de gelijktijdige aanwezigheid van een substantie op verschillende plaatsen, de zogenaamde multilocatio, ondenkbaar en moet het bestaan van accidentia sine subjecto worden ontkend. Descartes, die er altijd erg op uit was met de kerk op goede voet te blijven en die nooit verlegen was om theorieën, heeft wel geprobeerd zijn systeem met de eucharistie in overeenstemming te brengen door middel van hypothesen ad hoc, maar die pogingen hebben evenmin resultaat opgeleverd als de latere theorie der transsubstantiatie van de mechanicus Varignon.

Al de logische bezwaren, die de theorie van Descartes nog eens had geaccentueerd, kon nu echter Leibniz gemakkelijk oplossen door zijn fundamentele stelling dat het wezen der materie niet gelegen is in de uitgebreidheid, maar in een inwendige onstoffelijke activiteit, een force active, die, verenigd met het passieve principe, de materia prima, de waarlijk reële substanties, de monaden, vormt. Een lichaam is nu een verzameling van een oneindig aantal continu met elkaar samenhangende monaden, die het, naar een beeld van Leibniz zelf, bevat zoals het ordinatenoppervlak van een kromme het zijn ordinaten doet; die monaden zijn zelf zonder uitgebreidheid, maar ze doen zich gezamenlijk voor als een res extensa met al de primaire en secundaire eigenschappen der

* ‘ad dexteram’: ‘aan de rechterhand van de Vader’.

* ‘vere’: ‘waarlijk, werkelijk en stoffelijk’.

* ‘ad modum’: ‘op geestelijke wijze’.

[p. 157]

materie, omdat God gewild heeft dat alles in de wereld zou verlopen in pondere, in numero et in mensura.^*

Hoe Leibniz nu op grond van deze nieuwe theorie der materie het mysterie der eucharistie wel begrijpelijk meent te kunnen maken voor de menselijke rede, zal hier niet verder worden uiteengezet; wellicht heeft de lezer toch reeds de indruk gekregen dat de bespreking zich thans toch wel heel ver verwijdert van het onderwerp van deze verhandeling, dat immers in de ontwikkeling der mechanica bestond. Die indruk is echter onjuist. Zolang men over Leibniz spreekt, die een van de meest veelzijdige genieën is waarvan de geschiedenis van het denken melding maakt, staan alle gebieden van ons weten in even onmiddellijke samenhang als de monaden het in een organisme doen. Want inderdaad: wanneer men zich afvraagt hoe die force active, die entelechie, die in de theologie de praesentia realis van Christus in het Heilig Avondmaal kan verklaren en die in de metafysica de theorie der voorbeschikte harmonie mogelijk maakt, waardoor Leibniz de raadselen van de samenhang van lichaam en ziel kan verklaren, zich empirisch aan ons voordoet, dan zijn we ineens weer midden in de mechanica: het blijkt namelijk dat die inwendige kracht bij een bewegend lichaam wordt gemeten door het produkt van de massa en het kwadraat van de snelheid, zodat zij zich slechts door een getallenfactor onderscheidt van onze kinetische energie en dat ze bij een rustend lichaam als vis mortua toch in ieder [geval] zeer nauw verwant is met wat wij potentiële energie noemen. In de materietheorie van Leibniz, waarin de lotgevallen der lichamen worden bepaald door de spontane veranderingen van de inwendige activiteit, vindt men dus de kern van de zuiver energetische beschouwingswijze van de natuur, die aan het eind van de negentiende en het begin der twintigste eeuw haar vurige aanhangers heeft gehad.^*

Leibniz zelf heeft de waarde mv² (produkt van de massa en het kwadraat van de snelheid) als maat voor de kracht van een bewegend lichaam in de plaats gesteld van de cartesiaanse waarde mv (produkt van massa en snelheid). De argumentatie waarmee hij dit doet berust op misverstand. Hij beweert namelijk dat de cartesianen gevolg en oorzaak verwarren wanneer ze niet de quantitas potentiae, dat is het vermogen tot beweging, maar de quantitas motus, dat is de beweging zelf, als invariant beschouwen. Maar zo redenerende hecht hij een overdreven waarde aan de inderdaad ongelukkige term van quantitas motus, die in de bovendien onjuiste vertaling ‘hoeveelheid van beweging’ nog in de tegenwoordige mechanica voortleeft. Wanneer de cartesianen die grootheid impuls hadden genoemd of er de scholastische terminus impetus voor hadden gebruikt, zou er a priori niet de minste reden meer zijn om de levende kracht boven de impuls of de impetus als maat voor het vermogen van een bewegend lichaam om weerstanden te overwinnen, te verkiezen. En bij nader onderzoek blijkt die reden evenmin te bestaan. Sedert d'Alembert weten we dat de impuls van een stoffelijk punt evenredig is met de tijd waarin het door een constante remmende kracht tot rust wordt gebracht

* ‘in pondere’: ‘naar gewicht, getal en maat’.

* ‘energetische beschouwingswijze’: De energetische beschouwingswijze werd rond de eeuwwisseling met kracht naar voren gebracht door de Duitse fysisch-chemicus en filosoof Wilhelm Ostwald (1853-1932). Energie had volgens Ostwald een hogere graad van werkelijkheid dan de materie en daarom was energie het enige verklaringsprincipe in de natuurwetenschappen.

[p. 158]

en de levende kracht met de weg waarover het onder de werking van die kracht kan blijven bewegen. Om dit inzicht te verwerven hebben de beoefenaren der mechanica echter een halve eeuw moeten twisten. Het is een strijd geweest die, zoals dat in die tijd met natuurwetenschappelijke kwesties meer ging - de controversies over de vorm van de aarde zijn er een treffend voorbeeld voor -, de gehele intellectuele wereld interesseerde. Voltaire en Madame du Châtelet hebben er elkaar zelfs over bestreden en Immanuel Kant heeft er zijn eerste werk aan gewijd.

Ik moet nu, over Leibniz sprekende, nog een andere bijdrage van hem tot de mechanica vermelden, die met de besprokene de eigenschappen gemeen heeft dat ze eigenlijk geheel buiten de theorie van Newton omgaat, dat ze voortvloeit uit metafysische beschouwingen en dat ze in de loop van de achttiende eeuw in hoge mate de belangstelling van alle wetenschappelijk ontwikkelde kringen heeft getrokken. Het is het zogenaamde principe der kleinste actie, waarin wordt uitgesproken dat voor de werkelijke bewegingen in de natuur een zekere grootheid, die de som is van de produkten der bewegende massa's met de wegen die ze doorlopen en de snelheden waarmee ze dit doen, een extreme waarde heeft, vergeleken met fictieve bewegingen tussen dezelfde eindpunten, die weinig van de werkelijke afwijken. Dit principe, dat Leibniz nooit heeft gepubliceerd maar waarvan men de invloed op verschillende plaatsen in zijn werken kan nagaan, is het eerst in 1744 in het openbaar uitgesproken door de president der Berlijnse Academie, Maupertuis. Deze formuleert het zo dat voor alle natuurlijke bewegingen de actie een minimum is en dat ook voor lichamen in rust de actie bij een intredende kleine beweging zo klein mogelijk blijft. Hij hecht er vooral waarde aan omdat hij in deze klaarblijkelijk natuurlijke spaarzaamheid met de actie een onomstotelijk bewijs ziet van het bestaan van een wijze Schepper, die de wereld zo economisch mogelijk beheert; hij is overtuigd dat hij met dit principe het metafysisch beginsel heeft gevonden waaruit de gehele mechanica te deduceren zal zijn. De wetenschappelijke toepassingen die Maupertuis van het met zoveel ophef aangekondigde beginsel van de kleinste actie heeft gemaakt, zijn hoogst onbeduidend en het is dan ook niet aan hem, maar aan zijn geniale tijdgenoot Euler te danken dat het zich tot een bruikbaar principe heeft kunnen ontwikkelen. De filosofische beschouwingen echter die hij in zijn Essay de cosmologie geeft over het metafysische doel dat hij met zijn theorie vervolgt, zijn als illustratie van de nauwe samenhang die er bij de achttiende-eeuwse mechanici en fysici tussen religieuze of filosofische overtuigingen en natuurwetenschappelijke opvattingen bestaat, hoogst merkwaardig.

Ze leren vooral in wat voor misverstand men verkeert wanneer men het enge verband dat er in de latere achttiende en in de negentiende eeuw tussen mechanistische natuurbeschouwing en materialistische filosofie en wereldbeschouwing heeft bestaan, als een essentiële consequentie van de toepassing der mechanica op het natuuronderzoek beschouwt. Het valt namelijk op dat

[p. 159]

Maupertuis en met hem verschillende andere schrijvers er voortdurend de nadruk op leggen dat de overtuiging van het bestaan van een goddelijk wereldbestuur niet in strijd is met de aanname van de streng mechanische wetmatigheid van het natuurgebeuren, waarbij men het woord mechanisch dan echter niet figuurlijk in de zin van machinaal moet opvatten, maar in de ruimere zin van ‘onderworpen aan de algemene axiomata der bewegingsleer’. De ongelukkige omstandigheid dat mechanica etymologisch op werktuigkunde schijnt te duiden, heeft het doordringen van dit inzicht altijd in de weg gestaan; de tegenstelling die filosofische schrijvers wel gemaakt hebben tussen dynamisme en mechanisme, waarbij ze dan Leibniz, die een mechanistisch filosoof par excellence is, als tegenstander van een mechanistische natuurwetenschap laten optreden, heeft het bepaald tegengewerkt.

De nadruk waarmee het bedoelde punt herhaaldelijk besproken wordt, wekt de indruk dat de mechanistische natuurbeschouwing in de eerste helft der achttiende eeuw een strijd op twee fronten heeft moeten voeren, een tegen een geloof dat in de vermogens van de menselijke geest geen vertrouwen had, een tegen een ongeloof dat zijn vertrouwen alleen daarin stelde. Vandaar de herhaalde verzekeringen van Leibniz dat de natuur streng mechanisch moet worden verklaard, maar dat de axiomata der mechanica zelf van metafysische oorsprong zijn; vandaar ook de woorden van Maupertuis: ‘Une mécanique aveugle et nécessaire suit les desseins de l'Intelligence la plus éclairée et la plus libre.’^* En we vinden hier nog eens opnieuw de verklaring waarom men Newtons axiomata niet als een definitieve basis der mechanica kon aanvaarden, waarom de cartesianen vasthielden aan hun behoud van impuls, Leibniz aan de force active, Maupertuis en Euler aan de minimum-actie.

Ik kan hier op de in meer dan een opzicht merkwaardige geschiedenis van het principe der kleinste actie, dat zich in het eind van de achttiende en het begin van de negentiende eeuw in de handen van Lagrange, Jacobi en Hamilton tot een der meest fundamentele principes der mechanica zou ontwikkelen, niet ingaan. Twee opmerkingen moet ik echter erover maken. De eerste is deze dat met dit principe de teleologische beschouwingswijze der natuur, die in de zeventiende eeuw sterk op de achtergrond was gedrongen, haar plaats in de fysica ten dele weer herovert, om dan verder in de achttiende-eeuwse natuurbeschouwing niet meer te verdwijnen. Leibniz, die al niet meer zo vijandig staat tegenover de scholastiek als men dat in het begin van de zeventiende eeuw had gedaan en die bijvoorbeeld voor de inwendige activiteit heel rustig de scholastische terminus forma substantialis gebruikt, aanvaardt in zijn filosofie volmondig de causae finales of doeloorzaken naast de causae efficientes. En Maupertuis is van oordeel dat men bij de verklaring der natuurverschijnselen niet alleen moet trachten ze uit de eigenschappen der lichamen af te leiden, maar tevens moet letten op het doel dat in het natuurgebeuren kan worden beoogd.

De tweede opmerking betreft de grote beroering die de toch tamelijk

* ‘une mécanique aveugle’: ‘een blinde en noodzakelijke mechanica volgt de bedoelingen van de meest verlichte en vrije Intelligentie’.

[p. 160]

abstracte wetenschappelijke aangelegenheid der kleinste actie in brede kringen heeft verwekt, toen in 1751 de opzienbarende onthulling werd gedaan dat het principe in de vorm waarin Maupertuis het had uitgesproken, in zoverre onjuist was dat de actie bij bewegingen zoals ze in de natuur verlopen, ook wel een maximum kon zijn (waarmee het hele spaarzaamheidsbewijs voor het bestaan van God in het water viel) en dat het bovendien reeds door Leibniz in juistere vorm was opgesteld. Die onthulling kwam van Samuel König, een Zwitserse mathematicus die een tijdlang in nauwe relatie heeft gestaan tot Voltaire en Madame du Châtelet, welke laatste hij in de hogere wiskunde onderwees en die later een geziene persoonlijkheid is geworden aan het hof van de stadhouder in Den Haag. Het gevolg was het heftige conflict van de Berlijnse Academie met König, waarin Maupertuis, die gevoelig in zijn ijdelheid gekwetst was, met ondersteuning van Euler zo hoogst onbillijk is opgetreden en waarin Voltaire heeft ingegrepen met de satirieke Histoire du docteur Akakia, waarin zowel Maupertuis als Euler op de meest onbarmhartige wijze worden bespot. Dit geschrift, dat in Berlijn niet mocht verschijnen maar dat er, in Holland gedrukt, toch doordrong, werd de directe aanleiding van de breuk van Voltaire met de koning, die het libel wel door de beul openlijk kon laten verbranden, maar die de president van zijn Academie nooit meer heeft kunnen herstellen in de positie die hij voor die tijd in veler oog had ingenomen.

De weinig sympathieke wijze waarop Euler, die toch beter dan iemand anders kon weten hoezeer Maupertuis ongelijk had, in deze zaak is opgetreden, hangt, hoewel materiële motieven er ook wel niet vreemd aan zullen zijn geweest, waarschijnlijk eveneens ten nauwste samen met de nauwe relatie waarin ook in zijn werk theologische en mathematische gezichtspunten tot elkaar stonden. Euler was namelijk een streng rechtzinnig protestant, die in geloofszaken fanatiek partij trok. Dat fanatisme toont hij vooral wanneer het erom gaat de filosofie van Leibniz, zoals die door Wolff verder was ontwikkeld, te bestrijden, wat hij bijvoorbeeld uitvoerig en niet onvermakelijk doet in de Lettres à une princesse allemande. Het is zeer aannemelijk dat het principe der kleinste actie in de teleologische wending die Maupertuis eraan gegeven had, hem om religieuze redenen zeer ter harte ging en dat hij het niet heeft kunnen verdragen dat het met de gehate filosofie van Leibniz in verband werd gebracht.

Over de samenhang van theologie en wiskunde in de zeventiende en achttiende eeuw zou nog veel gezegd kunnen worden. Men zou bijvoorbeeld tal van mathematici kunnen noemen, vooral in Engeland, die tevens theoloog waren of dit later werden, zoals Oughtred, Wallis, Barrow, Pell; anderen, die althans sterk theologisch geïnteresseerd zijn, zoals Napier, de uitvinder der logaritmen, die een commentaar op de Openbaring van Johannes schreef, waarin hij aantoont dat de Antichrist de paus van Rome is, en Newton, die in zijn werken dezelfde Openbaring en bovendien de profetieën van Daniël

[p. 161]

uitvoerig heeft behandeld; men zou nog kunnen wijzen op menige onverwachte gedachtenverbinding tussen mathematische vondsten en inzichten en godsdienstige overtuigingen in de werken van de Bernoulli's en Euler.

Liever dan hierover uit te weiden wil ik dezelfde samenhang nog van de andere kant uit toelichten door een voorbeeld te noemen van de toepassing van mathematische methoden in de theologie. Het is te vinden in de Demonstratio evangelica van de Franse bisschop Pierre Daniel Huet, die niets minder nastreeft dan een complete axiomatisering van de christelijke godsdienst. Het gaat streng euclidisch in zijn werk: zeven definitiones; twee postulaten, waaronder een de eis bevat dat de lezer zal komen met een gewillig en naar waarheid strevend gemoed, niet met weerbarstige en stijfhoofdige gevoelens; vier axiomata, zoals: alle vermogen tot profeteren is uit God. Daarop volgen dan tien proposities, bewezen volgens alle regelen der mathematische kunst. De bewijzen onderscheiden zich van die van mathematische stellingen echter vooral door hun omvang: zo eist de vierde propositie: ‘De boeken van het Oude Testament zijn echt’, een bewijs van 473 bladzijden, de negende: ‘Jezus van Nazareth is de Messias’, een van 517 bladzijden.

Een dergelijke toepassing van de wiskundige methode is natuurlijk tevens een symptoom van een algemene neiging in de zeventiende en achttiende eeuw om van de helderheid en de overtuigende werking van de mathematische betoogtrant ook op andere gebieden partij te trekken. Spinoza's Ethica is er het beroemdste voorbeeld van; een duidelijke formulering van de overtuiging die eraan ten grondslag ligt, vindt men in de verklaring van Fontenelle in de voorrede van zijn Eloges: ‘Un ouvrage de Morale, de Politique, de Critique, peut-être même d'Eloquence en sera plus beau, s'il est fait de main de Géomètre’.^*

Natuurlijk rijst tegen de toepassing van de wiskunde in filosofische en theologische beschouwingen ook wel verzet; vooral in piëtistische kringen zag men de rationalisering der theologie die men er als gevolg van vreesde, met lede ogen; de uitlating van de piëtistische professor Francke uit Halle dat hij iemand die Euclides bestudeerde niet meer tot christen kon maken en de mening van zijn orthodoxe collega Lange dat de wiskunde een falsa eruditio is die rechtstreeks naar het atheïsme voert, zijn er sprekende uitingen van.

Andere theologen staan ook wel kritisch tegenover de wiskunde, maar met meer begrip en inzicht. Ik wil als slot van dit artikel hiervan een historisch belangrijk voorbeeld behandelen, namelijk dat van de Engelse filosoof en theoloog Berkeley, die in 1734 door zijn kritiek op de fluxierekening van Newton de stoot heeft gegeven tot een jarenlang voortgezette polemiek over de grondslagen van de infinitesimaalrekening, die voor de verheldering der denkbeelden van waarde is geweest.

Berkeley publiceerde in dat jaar een geschrift The Analyst met de ondertitel An address to an infidel mathematician, dat zeer waarschijnlijk gericht is geweest tegen de bekende astronoom Halley en waarin hij betoogt dat de

* ‘Un ouvrage de Morale’: ‘Een werk op het terrein van de zedeleer, de politiek, de kritiek, misschien ook zelfs de welsprekendheid, zal er schoner door worden als het komt van de hand van een wiskundige.’

[p. 162]

redeneringen van Newtons fluxierekening zo zeer spotten met alle redelijkheid, dat het onbegrijpelijk is dat iemand die zijn logisch denken in voldoende mate kan verloochenen om die redeneringen te volgen, verstandelijke bezwaren kan inbrengen tegen de dogma's der christelijke religie. Om dit toe te lichten gaat hij na hoe Newton de fluxie afleidt van de functie y = xⁿ. Hij doet dit door aan x een kleine aangroeiing te geven, voorgesteld door de letter o en nu de bijbehorende aangroeiing van y uit te rekenen. Dat wordt dan

Δ y = (x + o)ⁿ - xⁿ = n.o.x^n-1 + ... + oⁿ

De verhouding der bijeenbehorende aangroeiingen van y en van x is nu

n.x.^n-1 + n(n-1)/2. o.x^n-2 + ... o^n-1

Hierna vervangt Newton o door de waarde nul, laat dus alle termen verdwijnen die nog o bevatten en vindt voor de gevraagde fluxie nx^n-1, wat ook inderdaad de waarde is die de differentiaalrekening daarvoor aangeeft.

Berkeley verklaart dit gehele betoog voor een groot sophisma. De redenering, zegt hij, is gebaseerd op de onderstelling dat x aangroeit met een bedrag o; o is dus essentieel verschillend van nul; het is dus ongeoorloofd nu achteraf o gelijk aan nul te stellen.

En daaruit volgt nu een geharnast betoog tegen de gehele behandeling van de infinitesimaalrekening door Newton en Leibniz, één felle en niet eindigende aanklacht tegen al die oneindig kleine grootheden, kleinste tijdsdelen, ontstaande aangroeiingen, beginnende snelheden en beginnende snelheden van beginnende snelheden, waarvan hun beschouwingen vervuld zijn. Wie dat alles kan slikken meent Berkeley, ‘needs not be squeamish about any point in divinity’. Wie een derde fluxie aandurft behoeft voor de Drieëenheid niet terug te deinzen. En als er nu toch eenmaal mysteriën moeten worden aanvaard, dan nog maar liever in Divine Faith dan in Human Science.

Het is natuurlijk voor de hedendaagse wiskundige duidelijk dat de bisschop, strikt genomen, met zijn kritiek volkomen gelijk had. Het is inderdaad ongeoorloofd, o gelijk aan nul te stellen; men mag o alleen tot nul laten naderen. Voor de ontwikkeling der wiskunde kunnen we dankbaar zijn dat de produktieve mathematici der achttiende eeuw minder scrupuleus zijn geweest dan hun geestelijke criticus.

Met de bovenstaande beschouwingen is het onderwerp waarover dit opstel handelt, natuurlijk niet in het minst uitgeput. Wellicht heeft het echter enige indruk kunnen geven van de grote betekenis die het wiskundig denken in de zeventiende en achttiende eeuw voor de ontwikkeling der natuurwetenschappen heeft gehad en van de sterke invloed die het op de gehele cultuur van die tijd heeft uitgeoefend.