Het toeval van de werkelijkheid
(1983)–H.B.G. Casimir–Een halve eeuw natuurkunde
[pagina 369]
| |
Appendix B. Natuurkunde omstreeks 1930Hoewel dit appendix wat technischer is dan het boek zelf is het toch in dezelfde geest geschreven: het beoogt niet een volledig en goed gedocumenteerd overzicht te geven, het vertelt over mijn persoonlijke indrukken. Ik hoop dat wat ik schrijf ook hier feitelijk correct is, maar keuze en nadruk worden bepaald door persoonlijke voorkeur en ervaring. Omstreeks 1930 kwam de niet-relativistische quantummechanica langzaamaan in het technische stadium - in de zin van hoofdstuk 2; industriële of commerciële toepassingen waren nog niet in zicht. Laat ons eerst eens kijken naar het onderzoek van atoomspectra. Men verwachtte niet meer dat het tot nieuwe natuurwetten zou leiden. Ook was men niet van mening dat dit onderzoek nodig was om verdere bevestiging van de grondbeginselen der quantummechanica te krijgen. De situatie wordt goed gekenschetst door een opmerking van O. Klein. Ik zei eens tegen hem dat het aardig zou zijn als er grote automatische rekenmachines zouden bestaan die nauwkeurig de eigenwaarden zouden kunnen bepalen van Schrödinger-vergelijkingen voor een groot aantal elkaar beïnvloedende elektronen. ‘Maar zulke machines zijn er,’ zei Klein, ‘ze bestaan uit een ontladingsbuis en een spectroscoop.’ Dit wilde overigens niet zeggen dat het onderzoek van ingewikkelde spectra geen interessante zaak kon zijn, maar het moest op eigen merites worden bekeken. Er was vooral nog rijkelijk gelegenheid voor verbetering van wiskundige methodes. Gedurende mijn eerste maanden in Kopenhagen was B. Trumpy uit Noorwegen te gast in Bohrs instituut. Hij had de intensiteiten van een aantal spectraallijnen gemeten en vergeleek die nu met waarden die hij berekende. Daarvoor had hij benaderde golffuncties nodig die hij bepaalde door numerieke integratie waarbij | |
[pagina 370]
| |
hij een met de hand bewogen rekenmachinetje gebruikte. Hij was een harde werker en kon uren achter elkaar zitten rekenen, maar ongeveer eens per uur stond hij op, liep een paar rondjes om de tafel op zijn handen, en rekende dan rustig verder. Ik weet niet wat ik meer bewonderde, zijn numerieke of zijn atletische vaardigheid. Het onderwerp is in recente jaren tot nieuw leven gekomen door de laserfysica die zeer verfijnde experimenten mogelijk maakt. Het is vermakelijk dat men ook toen heel goed lasers zou hebben kunnen bedenken en maken. Het denkbeeld van gestimuleerde emissie was sinds Einsteins verhandeling uit 1917 welbekend. Geïnverteerde bezetting van energieniveaus moet voor gasontladingsexperts niet ondenkbaar zijn geweest en de optische techniek die werd gebruikt om interferometers te maken was ruimschoots voldoende om een laser aan de gang te krijgen. In werkelijkheid kwamen lasers pas veel later. Tegen het einde van de jaren twintig en het begin van de jaren dertig begon wel een andere, nieuwe lijn in de spectroscopie, namelijk het onderzoek van de zogenaamde hyperfijnstructuur. In de theorie van Rutherford en Bohr wordt aangenomen dat de kern een puntvormige lading is (met lading Z. e en massa M). Dat bleek volledig voldoende te zijn om de structuur van spectra te kunnen verklaren. Toen men echter spectra zeer nauwkeurig bekeek, met een spectroscoop van zeer groot scheidend vermogen, ontdekte men dat vele tot dan toe als enkelvoudig beschouwde spectraallijnen in werkelijkheid weer uit een aantal lijnen bestaan. Dat zou men de hyperfijne structuur kunnen noemen; gangbaarder is het germanisme hyperfijnstructuur en die term zal ik ook maar gebruiken. Reeds in 1924 had Pauli opgemerkt dat deze hyperfijnstructuur moet samenhangen met andere kerneigenschappen dan lading en massa en hij had het vermoeden uitgesproken dat de kern een impulsmoment zou bezitten.Ga naar eind1 Wat later analyseerden Goudsmit en Back zeer zorgvuldig de hyperfijnstructuur van het bismuthspectrum en ze slaagden erin zowel het impulsmoment van de kern als (bij benadering) het magnetisch moment te bepalen. Sedertdien heeft het onderzoek van de hyperfijnstructuur nuttige, zij het ook bescheiden bijdragen tot onze kennis van de atoomkernen geleverd. In Kopenhagen stond Ebbe Rasmussen aan het hoofd van een groepje dat werk deed op dit gebied, en de | |
[pagina 371]
| |
Duitse natuurkundige Kopfermann, die ik in mijn zesde hoofdstuk noemde, was daar vaak te gast. Gedurende een van de eerste dagen van de conferentie in Kopenhagen in 1929 vroeg Goudsmit me of ik de wisselwerking van een magnetisch kernmoment en een s-elektron kon uitrekenen, bijvoorbeeld het elektron in de grondtoestand van een waterstofatoom. Dat was toen nog een onopgelost vraagstuk. In dergelijke toestanden is de golffunctie bolsymmetrisch rond de kern en ze is in het middelpunt, dus ter plaatse van de kern, niet nul. Stellen we ons nu voor dat er zich in de kern een magnetische dipool met moment μ bevindt en dat het magnetische moment van het elektron is uitgesmeerd volgens de waarschijnlijkheidsverdeling die wordt gegeven door de absolute waarde van het kwadraat van de golffunctie en proberen we dan de wisselwerking te berekenen, gebruik makende van de gewone formule voor de wisselwerking van twee dipolen, dan blijkt dat de integraal divergeert. Ik had die keer werkelijk het spreekwoordelijke geluk van de beginner: ik zag meteen hoe je het probleem kon aanpakken en in een paar dagen had ik de oplossing uitgewerkt.Ga naar eind2 De zaak is dat in Diracs relativistische theorie van het elektron het magnetische moment van het elektron het resultaat is van een stroomdichtheid. Dat had een diepe indruk op me gemaakt en die werd nog versterkt door de elegante vorm van de stroomverdeling in de grondtoestand van waterstof die in het boek van Weyl expliciet was neergeschreven. Men kan haar zelfs met woorden beschrijven. De ladingsdichtheid neemt exponentieel af met groeiende straal. De stroomdichtheid kan worden beschreven door te zeggen dat de lading tussen twee naburige concentrische boloppervlakken om de z-as ronddraait als een vast lichaam met een dusdanige hoeksnelheid dat de snelheid aan de equator onafhankelijk van de straal gelijk is aan αc. Daar is α de zogenaamde fijnstructuurconstante, a = e2/ℏc ≈ 1/137.Ga naar voetnoot* Achtergaf gezien is het eigenaardig dat blijkbaar niemand op het idee was gekomen een stroom te associëren met de elektronenspin voor Dirac zijn relativistische theorie formuleerde. Toch zou dat in Pauli's niet-relativistische theorie heel goed gekund hebben. Men hoeft namelijk alleen maar de formule uit de macroscopische elektrodynamica | |
[pagina 372]
| |
i = c curl M toe te passen. Voor een s-toestand met spin in de z-richting geeft dat als resultaat: 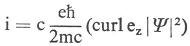 De formule voor het magneetveld dat door deze stroomdichtheid in de oorsprong wordt opgewekt is dan bijna een tautologie. Een kleine historische uitweiding. Kort nadat Ørsted had gevonden dat een elektrische stroom een kracht uitoefent op een magneetnaald (hijzelf sprak niet over een stroom maar over het elektrisch conflict)Ga naar voetnoot* formuleerde Ampère de hypothese dat alle magnetisme het gevolg is van stromen. Dat idee werd overgenomen door Maxwell en is ook een essentieel onderdeel van Lorentz' elektronentheorie. Nu zag het er even naar uit dat Goudsmits en Uhlenbecks idee van een roterend elektron de situatie zou wijzigen, maar Diracs theorie maakte aan die vrees een einde en daar was ik erg blij om. Ik vond - en vind nog - magnetisme een verward en verwarrend onderwerp tenzij je van het begin af aan uitgaat van stromen. Magnetische momenten kunnen later worden ingevoerd, maar alleen als soms handig rekenhulpmiddel zonder fysische betekenis. Omdat ik de stroomverdeling in een s-toestand kende was het niet moeilijk het door deze stroomverdeling in de oorsprong opgewekte magneetveld uit te rekenen. Je had niet veel meer nodig dan het formuletje voor de tangentenboussole - het practicum was toch wel ergens goed voor geweest - en verder moest je een eenvoudig integraaltje uitrekenen. Voor het veld in de oorsprong vind je:  waar Ψ (o) de genormaliseerde Schrödinger-functie in het middelpunt is. Het is dan heel eenvoudig de wisselwerkingsenergie te berekenen. Goudsmit produceerde direct een listige schatting van |Ψ(o)|2 en het bleek dat mijn formule met succes kon worden toe- | |
[pagina 373]
| |
gepast op het Na-spectrum en in enkele andere gevallen. Hij vond echter dat ik de zaak maar alleen moest publiceren. Ik besteedde dus een deel van mijn tijd in Kopenhagen aan het schrijven van een stukje en dat stuurde ik naar Goudsmit. Ik heb nog een kopie van de tekst en ik begrijp nu heel goed dat Goudsmit niet goed wist wat hij ermee aan moest. Het was nogal knullig geschreven, al was het resultaat juist. Pas veel maanden later stuurde hij het terug met enkele voorstellen hoe ik het kon verbeteren, maar voor ik daarmee klaar was, was de bekende verhandeling van Fermi verschenen. Ik moet toegeven dat dat wel een teleurstelling was. En het resultaat was nog belangrijker dan men toen kon voorzien. Er volgde namelijk uit dat atomaire waterstof een absorptie en emissielijn moet hebben met een golflengte van drieëntwintig centimeter. (Het bestaan van een dergelijke radio-spectraallijn had men meteen kunnen voorspellen, de waarde van de golflengte kon men pas kwantitatief berekenen nadat Stern het magnetisch moment van het proton had bepaald.) Later hebben de radio-astronomen de emissie van deze straling voor verschillende gebieden van de ruimte onderzocht en dit heeft veel bijgedragen tot onze kennis van de bouw van ons melkwegstelsel. Het zou prettig zijn geweest als eerste de daaraan ten grondslag liggende theorie te hebben gepubliceerd.Ga naar voetnoot* Misschien was het maar beter zo. Ik was toen toch al verwaand genoeg, en het werk was niet verloren. Ik heb er later van kunnen profiteren. Belangrijk werk werd destijds ook verricht - zowel experimenteel als theoretisch - aan atomaire botsingen. Mott, die zijn stage in Kopenhagen juist beëindigde toen ik aankwam, vond op dat gebied een aantal fraaie resultaten.Ga naar voetnoot† De overige toepassingen van de quantummechanica gingen in twee richtingen. In de richting van moleculen en gecondenseerde materie, vooral vaste stoffen. Ik heb al verteld hoe Pauli bezwaar maakte tegen het onexacte karakter van de verdere uitwerking van de Heitler-London theorie van de chemische binding. Het | |
[pagina 374]
| |
komt me voor dat men ook vandaag nog enige twijfel kan koesteren over de betrouwbaarheid van de berekeningen - nu uitgevoerd met grote computers - van bindingsenergieën, enzovoort. Pauli had ook wat tegen op de theorie van de vaste stof. Niemand zal echter kunnen ontkennen dat juist daar de theorie bijzonder vruchtbaar is geweest. Het is interessant de lijnen van onderlinge beïnvloeding nog eens na te gaan. In het begin van onze eeuw was de soortelijke warmte van vaste stoffen een verschijnsel waarvan de analyse de weg wees naar de quantumtheorie. Daarna was het eigenlijke front op het gebied van de spectra. En ten slotte ging de daaruit gewonnen quantummechanica haar oude schuld aan de vastestoffysica - met rijkelijke interest - terugbetalen. Quantummechanica ging ook in de richting van kleinere dingen, van de kern. Daar was de situatie aanvankelijk heel wat minder duidelijk. De zaak was niet alleen dat de vergelijkingen te moeilijk waren om op te lossen, er waren veel fundamentelere problemen; er was nog geen sprake van dat de theorie in het technisch stadium was. Hoe stond het met Bohr zelf? Hij was maar matig geïnteresseerd in de verdere uitwerking van de wiskundige theorie. Ik hield me later bezig - geïnspireerd door een briljant idee van Oscar Klein - met de theorie van de asymmetrische tol, en daardoor kwam ik tot enkele nieuwe resultaten in de theorie van de representaties van de driedimensionale rotatiegroep en sommige van die resultaten kon ik generaliseren voor andere groepen. Het werk werd vastgelegd in de disseratie waarop ik op 3 november 1931 te Leiden promoveerde.Ga naar eind3 Die dissertatie - en een voorlopige mededeling - beschrijft ook wat tegenwoordig vaak de Casimir-operator wordt genoemd. Om dat in het juiste perspectief te doen zien, zou ik echter iets willen citeren uit een geestig Engels boekje How to be famous.Ga naar eind4 Onder het hoofd Plato zegt het onder meer: ‘Zijn eigen onnauwkeurige opvatting over platonische vriendschap is achterhaald. In zijn tijd was die echter wel een verbetering ten opzichte van het bestaande stelsel waarin men in het geheel geen platonische vriendschappen kende.’ Mutatis mutandis zou dit ook van Casimir-operatoren kunnen worden gezegd. Van tijd tot tijd vroeg Bohr me: ‘Hvordan staar det, med det | |
[pagina 375]
| |
her Rotationsvaesen’ (hoe staat het met dat rotatiegedoe), maar meer uit vriendelijkheid dan uit werkelijke belangstelling. In vaste-stoffysica was Bohr in beginsel wel geïnteresseerd; hij had een prachtig proefschrift geschreven over de elektronen-theorie van metalen,Ga naar eind5 en had daarin onder andere duidelijk laten zien dat vele experimenteel gevonden eigenschappen van metalen niet kunnen worden begrepen op grond van de klassieke theorie. Hij hield zich echter niet meer actief met het onderwerp bezig en in zijn instituut gebeurde er ook niet veel op dit gebied. Toch moet hij wel hebben betoogd dat hij verwachtte dat de quantum-mechanica de problemen weldra zou oplossen: in Bohrs verzameling van overdrukken was de beroemde verhandeling van Bloch over elektronen in metalen met een opdracht van Pauli - die niet van vaste-stoffysica hield maar wel wist wat een goede verhandeling was -: ‘Aus dem beiliegenden Separatum von Bloch wirst Du sehen, dass dein Triumf über die Gelehrten vollständig ist.’ Evenmin was Bohr toen zelf al erg actief op het gebied van kernfysica: dat zou een paar jaar later komen, bijna als een tweede jeugd. Wel moedigde hij Gamow aan; dat moet Gamow geloofwaardiger hebben gemaakt in de ogen van Rutherford en zo ook enige invloed hebben gehad op de eerste experimenten van Cockcroft en Walton. Bohrs eigen werk bestond in de jaren dat ik in Kopenhagen was vooral in het verfijnen en verdiepen van zijn denkbeelden over de ware betekenis van de quantummechanica en hij trachtte ook de grenzen van de geldigheid van de bestaande theorieën vast te stellen. Het eerste probleem dat hij met me besprak was een nadere uitwerking van een mededeling die hij tijdens de 1929-conferentie had gedaan: hij had daar betoogd dat het magnetisch moment van een vrij elektron niet kan worden gemeten met een klassiek Stern-Gerlach experiment. We analyseerden samen een aantal in beginsel mogelijke experimentele werkwijzen en konden altijd laten zien dat de onzekerheid in de Lorentz-kracht groter was dan het effect dat gemeten moest worden. Nu is het waarschijnlijk erg dom van me, maar ik heb nooit begrepen dat dit van veel betekenis was. Vooral niet nadat Mott had laten zien dat uit de relativistische vergelijking van Dirac volgt dat elektronen die door een kern worden verstrooid, gepolariseerd worden, en wel des te meer naarmate hun snelheid nadert tot de snelheid van | |
[pagina 376]
| |
het licht.Ga naar eind6 Deze polarisatie kan worden waargenomen - en is vele jaren later waargenomen - met behulp van experimenten over tweevoudige verstrooiing. De golfvergelijking van Dirac was wel een grote stap vooruit, maar er zaten ernstige moeilijkheden aan vast: de toestanden met negatieve energie. Wellicht heeft Bohr eerst geloofd dat men daar vanaf zou kunnen komen door een zorgvuldige analyse van wat wel en wat niet waarneembaar was, maar dat lukte niet. Wat was nu precies de moeilijkheid? De Dirac-vergelijking heeft zowel oplossingen met positieve energie als oplossingen met negatieve energie. Voor een vrij deeltje bestaat er zelfs volledige symmetrie tussen toestanden met positieve en toestanden met negatieve energie. Nu zou men op het eerste gezicht kunnen denken dat dit geen echte moeilijkheid is en dat men de oplossingen met negatieve energie eenvoudig zou mogen vergeten. Per slot van rekening zou in de welbekende vergelijking de energie E ook negatief kunnen zijn. Zo eenvoudig kan men echter niet van de moeilijkheden afkomen. Men kan namelijk niet uitsluiten dat er overgangen plaatsvinden van toestanden met positieve energie naar toestanden met negatieve energie. Toepassing van de gebruikelijke stralingstheorie zou tot de conclusie leiden dat ieder elektron hoe langer hoe grotere negatieve energie krijgt, terwijl steeds meer stralingsenergie ervoor zorgt dat de totale energie constant blijft. Klein had laten zien dat volgens de Dirac-vergelijking een deeltje dat tegen een potentiaal-drempel van meer dan 2 mc2/e oploopt, een eindige kans heeft er doorheen te komen als elektron met negatieve energie. Misschien hoopte men destijds nog dat aan die uitstraling wel iets te doen was; voor de theorie van de beweging in een elektrostatisch veld was dat veel onwaarschijnlijker. Toen kwam Diracs gedurfde voorstel: neem aan dat alle toestanden met negatieve energie bezet zijn. (Daar elektronen zich gedragen volgens de Fermi-Dirac statistiek, de quantummechanische vorm van het Pauli-principe, is er in elke toestand maar plaats voor één elektron. Men spreekt - of liever sprak - in dit verband graag over de Fermi-zee. Dirac merkte verder op, dat | |
[pagina 377]
| |
er in die Fermi-zee wel eens een enkele onbezette plaats zou kunnen voorkomen; die zou zich gedragen als een positief deeltje. Zou dat niet het proton kunnen zijn? In die dagen bereikte het aantal deeltjes waar fysici aan geloofden een minimum: men dacht dat er alleen elektronen en protonen bestonden. Het atoomgewicht van een zuivere isotoop was altijd bij benadering gelijk aan een heel aantal malen het atoomgewicht van waterstof (of liever, 1/16 maal het atoomgewicht van zuurstof) en dat gehele getal werd geacht het aantal protonen in de kern te zijn. Een aantal elektronen moest dan worden toegevoegd ten einde de kernlading, Z.e, op de juiste waarde te brengen. Diracs heldhaftige poging het aantal deeltjes nog verder te reduceren, zodat er maar één elementair deeltje zou bestaan, bleek merkwaardig genoeg al spoedig het begin van een toeneming van het aantal elementaire deeltjes te zijn, en die toeneming gaat tot op de dag van heden door. Bohr was in het begin helemaal niet ingenomen met dat idee van de volle Fermi-zee. Dirac beweerde aanvankelijk dat je het elektrische veld van al die deeltjes met negatieve energie helemaal niet zou merken: er waren naar iedere kant evenveel en dus zouden hun velden elkaar compenseren, maar ik herinner me dat Bohr me uitlegde dat hij dat nonsens vond, want de divergentie van het veld moest oneindig zijn! Ik meen haast dat Dirac dit argument algauw heeft laten vallen. Het vervolg is bekend. Verschillende theoretici lieten zien dat er in een dergelijke Dirac-theorie altijd symmetrie bestaat tussen de elektronen en de gaten. Dus kon je op die manier nooit of te nimmer een proton krijgen. Toen stelde Dirac voor dat het gat een positief elektron zou kunnen zijn, maar waarom kreeg je nooit een positief elektron te zien? In 1932 vond Anderson, en even later vonden Blackett en Occhialini dat positieve elektronen werkelijk voorkomen, zij het alleen maar tijdelijk. Het model van gaten in de Fermi-zee is nuttig om het positief elektron te beschrijven en om zijn belangrijkste eigenschappen te verklaren, maar het is niet meer de manier waarop de theoretici er tegenwoordig over praten. In de theorie van de atoomspectra kan men zeggen dat de theorie van Dirac kleine relativistische correcties aanbrengt op de Schrödinger-vergelijking, maar de quantummechanica niet essentieel verandert. De meeste theoretici | |
[pagina 378]
| |
zullen tegenwoordig de Dirac-theorie liever beschouwen als een essentiële uitbreiding van de Schrödinger-theorie, namelijk als een eerste voorbeeld van een theorie waarbij het aantal deeltjes niet constant blijft. Men geeft er zich niet altijd rekenschap van dat bijna gelijktijdig met Diracs theorie van elektronen en (om te beginnen) protonen, maar iets eerder, het denkbeeld van positieve gaten ook zijn intree had gedaan in de vaste-stoffysica. Het lag ten grondslag aan Peierls' verklaring van het positieve Hall-effect. In het geval van de vaste stof is de Fermi-zee heel reëel: ze bestaat uit de elektronen in de valentieband. De lading van de Fermi-zee is geen probleem: die wordt gecompenseerd door de positieve ladingen van de atoomrompen. Aan de bovenkant van de valentieband hebben de elektronen een negatieve effectieve massa; in zoverre zijn ze te vergelijken met de elektronen met negatieve energie (die soms ezelselektronen werden genoemd omdat ze tegen de richting van een uitwendige kracht inliepen). Ik geloof niet dat er destijds veel aandacht werd besteed aan die analogie, tenminste niet in Kopenhagen. In moderne terminologie zou men kunnen zeggen: het Diracvacuüm is een halfgeleider met een bandafstand (band gap) van 2 mc2 of wel ruwweg een miljoen Volt. Omdat die afstand zo groot is, is er geen intrinsiek geleidingsvermogen. Dit vacuüm is echter n-type: de positieve atoomkernen zijn de dope. Evenals gaten in n-type germanium of silicium kunnen positronen een tijd overleven in onze n-type wereld. Positronium komt overeen met een exciton, enzovoort. Maar die typische halfgeleiderterminologie bestond nog niet in de jaren dertig. Hoe stond het met de quantumelektrodynamica? Dirac had laten zien hoe men het stralingsveld kon kwantiseren en zijn theorie was adequaat om de emissie en absorptie van straling, stralingsdemping, lijnbreedte en dergelijke te berekenen. Heisenberg en Pauli gaven een relativistisch invariante formulering. Fermi eveneens in een enigszins andere vorm. Enkele jaren later publiceerden Bohr en Rosenfeld een zorgvuldige analyse van onzekerheidsrelaties en meetmogelijkheden in elektromagnetische velden. Er bleef echter - vooral Ehrenfest legde daar de nadruk op - een fundamentele moeilijkheid bestaan, een moeilijkheid die zich ook al had voorgedaan in Lorentz' elektronentheorie. Wanneer | |
[pagina 379]
| |
men aanneemt dat het elektron een punt is, een straal nul heeft, dan heeft het elektromagnetische veld een oneindige energie. Als men in de klassieke theorie aanneemt dat het elektron een eindige straal heeft, dan rijst de vraag hoe die lading bij elkaar blijft: men moet een of andere niet-elektromagnetische spanning aannemen - de zogenaamde Poincaré-spanning - en de relativistische invariantie geeft moeilijkheden. Gelukkig zijn veel van de resultaten van de klassieke elektronentheorie ‘structuur-onafhankelijk’ maar zodra we over elektromagnetische massa gaan praten is dat niet meer het geval. Nu zijn in Diracs stralingstheorie - en ook in de ingewikkelder formulering van Heisenberg en Pauli - de termen die de wisselwerking van een elektron met het stralingsveld beschrijven beslist niet ‘structuur-onafhankelijk’: het elektron wordt duidelijk als puntvormig aangenomen. En ziet, reeds in een tweede benadering verschijnen er in de uitdrukking voor de energie divergente reeksen. In die dagen leefde de hoop dat iemand een elegante oplossing van dit probleem zou vinden. Tevens hoopte men dat men dan tevens de waarde van de fijnstructuurconstante theoretisch zou kunnen berekenen. Lang voor de geboorte van de nieuwe quantummechanica was Einstein onder de indruk geweest van het feit dat h en e2/c dezelfde dimensie hebben en ook van dezelfde orde van grootte zijn. Hij voelde dat dit betekende dat er verband bestaat tussen de kwantisering van lading en de kwantisering van energie, maar het lukte hem niet dit verder uit te werken. ‘Wie zal de quantumelektrodynamica maken?’ was een vraag die Landau herhaaldelijk stelde. Zijn de problemen van de quantumelektrodynamica werkelijk opgelost? In de jaren veertig werden geweldige vorderingen gemaakt. Het komt me echter voor - maar ik ben geen echte vakman op dit gebied - dat het probleem van de elektromagnetische massa niet echt is opgelost, maar dat men een systematische methode heeft ontdekt om het te ontlopen. Om het heel ruw te formuleren: men kan de elektromagnetische massa niet uitrekenen, maar men kan wel het verschil in elektromagnetische massa in verschillende situaties uitrekenen. De resultaten van deze zogenaamde ‘renormalisatietheorie’ zijn door het experiment bevestigd met haast ongelooflijke nauwkeurigheid, maar de hoop dat men daarbij ook de fijnstructuurconstante zou kunnen bepalen bleek | |
[pagina 380]
| |
ijdel: de theorie functioneert bij elke waarde van de fijnstructuurconstante, als ze maar klein is. In 1929 deed de grote sterrenkundige Sir Arthur Eddington een moedige poging de waarde van de fijnstructuurconstante en van vele andere natuurconstanten af te leiden uit een fundamentele theorie.Ga naar eind7 Daarbij zou 1/α gelijk moeten zijn aan het aantal componenten van een symmetrische tensor in zestien dimensies plus één. Dus 1/α = ½ × 16 × 17 + 1 of α = 1/137. Helaas heb ik zijn redenering totaal niet kunnen volgen. Dat zegt nog niet zoveel, maar geen van de theoretici die ik in ere heb, zijn daarin geslaagd. Zou er desalniettemin vroeger of later toch nog eens een korreltje waarheid worden ontdekt in deze vreemde beschouwingen? Een probleem dat bij enige conferenties in Kopenhagen werd besproken was het probleem van het continue bèta-spectrum. Alfa-deeltjes verlaten de kern met een scherp gedefinieerde energie. Bij bèta-deeltjes, bij elektronen die de kern verlaten, is dat heel anders: de energie is continu verdeeld over een groot interval. Zo is bijvoorbeeld voor radium E de gemiddelde energie ongeveer 340 keV, de maximum energie is 1 MeV. Toch werd het hoe langer hoe duidelijker dat de kernen voor en na het radioactieve uiteenvallen wel een scherp gedefinieerde energie hebben. Een tijd lang meende men dat er misschien gammastralen waren die de energiebalans in evenwicht brachten, maar zorgvuldige metingen van Lise Meitner toonden aan dat dit niet zo was. Twee mogelijkheden bleven over: ofwel de wet van behoud van arbeidsvermogen geldt niet voor alle radioactieve processen, ofwel de ontbrekende energie is verdwenen in de vorm van een nog niet ontdekte straling. Bohr neigde tot het eerste gezichtspunt; hij vond in elk geval dat men erop voorbereid moest zijn dat men het denkbeeld van een volledig behoud van arbeidsvermogen zou moeten opgeven. (Een soortgelijk denkbeeld in verband met de emissie van licht door atomen was in 1924 door Bohr, Kramers en Slater geopperd, maar het was weerlegd door de experimenten van Geiger en Bothe.) Pauli aan de andere kant was niet bereid het strenge behoud van arbeidsvermogen op te geven en hij postuleerde een nieuw deeltje, later door Fermi neutrino gedoopt, dat een kleiner of groter gedeelte van de energie zou afvoeren en dat zo weinig wisselwerking met de materie had dat het onopgemerkt | |
[pagina 381]
| |
kon ontsnappen. Het kon dus geen lading en geen magnetisch moment hebben. Pauli durfde zijn idee niet meteen te publiceren maar op 4 december 1930 stuurde hij een open brief aan de ‘groep der radioactieven’, aanwezig bij een bijeenkomst in Tübingen. ‘Waarde radioactieve Dames en Heren,’ luidt de aanhef en vervolgens zet hij zijn denkbeeld uiteen. Een essentieel punt is dat deze zondebok niet alleen voor de energiebalans zorgt, hij kan ook schijnbare discrepanties in impulsmomenten en in statistiek (in de zin van verwisselingssymmetrie) in orde brengen. Natuurlijk weten we allemaal dat Pauli's vermoeden volledig werd bevestigd, zowel door latere theoretische beschouwingen als door directe experimenten. Pauli zelf heeft de geschiedenis van dit onderwerp beschreven in een lezing die na zijn dood is gepubliceerd en die ook is te vinden in zijn verzamelde werken.Ga naar eind8 Op een goede dag - ik denk in 1930 - kreeg Bohr een brief van Pauli, die hij nogal moeilijk vond om te beantwoorden. Dus vroeg hij zijn vrouw een aardig briefje aan Pauli te schrijven en hem te zeggen dat Bohr zelf maandag zou schrijven.Ga naar voetnoot* Twee weken later kwam er een antwoord van Pauli aan mevrouw Bohr waarin hij schrijft dat het heel verstandig was geweest van Niels om te beloven dat hij maandag zou schrijven, maar zonder te zeggen op welke maandag. Maar hij moest zich vooral niet aan maandag gebonden voelen. Een brief op een andere dag geschreven zou even welkom zijn. Ik heb deze brieven niet kunnen opsporen. Het zou aardig zijn als de brief van Pauli aan Bohr een eerste mededeling over het neutrino zou bevatten, maar ik vrees dat dat niet mogelijk is. Pauli's brief aan ‘de radioactieven’ is gedateerd 4 december 1930 en het idee wordt ook vermeld in een brief aan Klein van 12 december 1930 en daar schrijft hij dat hij graag zou willen weten wat Bohr ervan zou denken, en dat betekent dat hij toen nog niet aan Bohr geschreven had. Ik ging weg uit Kopenhagen voor Kerstmis en hoewel ik voor een maand terugkwam in maart 1931, ben ik vrijwel zeker dat dit geval zich niet gedurende die maand afspeelde. Dus moet de opmerking die ik hierover elders maakte worden verwezen naar het rijk der opgesmukte fabelen.Ga naar eind9 |
|

