Logo DBNL
Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden (1878)

Bouwstoffen voor de geschiedenis der wis- en natuurkundige wetenschappen in de Nederlanden

(1878)–David Bierens de Haan–rechtenstatus Auteursrechtvrij

Vorige Volgende

BOUWSTOFFEN VOOR DE GESCHIEDENIS der WIS- EN NATUURKUNDIGE WETENSCHAPPEN IN DE NEDERLANDEN. door D. BIERENS DE HAAN.

XVII. Twee brieven van Ludolf van Ceulen.

1. Onlangs is de Bibliotheek der Leidsche Akademie in bezit gekomen van een zeldzaam werkje ‘Toet-steen van d'Algebra Spetiosa, door dirck d'hollander, Amsterdam 1669. 4o.’ 1), waarin twee brieven van ludolf van ceulen voorkomen, handelende over een vraagstuk uit het gebied der onbepaalde vergelijkingen, dat hij in zijn werk van den Circkel, konstige Vraghen, onder No. 57 had opgegeven.

Bovendien maken wij hier kennis met adrianus twilt, denkelijk onderwijzer in de wiskunde te Amsterdam in de eerste helft der zeventiende eeuw; en met nicolaas huybertszoon van percijn, die landmeter te Naarden was in het begin dier eeuw. Deze laatste schijnt een vertrouwd vriend van ludolf van ceulen geweest te zijn. Eindelijk met den schrijver dirk de hollander, Rekenmeester te Amsterdam, van wiens hand nog andere werken bekend zijn.

2. De vraag zelve is deze.

‘Vindt 3 Getallen, soodanigh als men van de cubo haarder || Zomme, af trekt elk getal insonderheyt, datter reste || dry rationale cubik getallen?’

De oplossing begint dus, in den eigenaardigen trant van dien tijd.

‘Supposons 1 f a, voor de somme van de 3 begeerde getallen.



illustratie

Daar resteert nu niets anders, dan dat de somme van dese drie getallen gelijk moet zijn || de eerst gesupposeerde somme....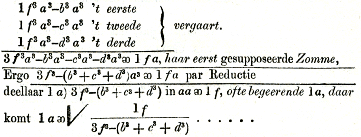



illustratie

Om de 3 voorsz. Cubik getallen te vinden, Supposons voor || den wortel van 't eerste Cubik tal d, en van 't tweede 12-x [hier en verder herhaaldelijk staat 12 foutief voor n], van 't derde 1 x.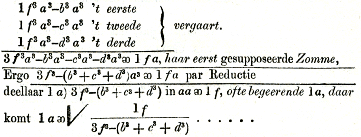



illustratie

* †

Nota. Wy supposeren nu dat k k is gelijk 3 f3-d3-n3....’

En hierop volgt verder de discussie der waarden.

3. Dat adrianus twilt zich op deze oplossing liet voorstaan, blijkt uit de ‘Aen den Konstgierigen Leser.’

‘In wat voor estime, den Hoog-geleerde Mathematicus Adrianus || Twilt, mijn Leermeester zalr: d'ontbindinge van dese Quaestie ge- || houden geeft, is my 't alderbest bekent, want hoe veel Penningen || men hem om d'instructie der selver, of copye daar van te hebben, ook || gepresenteert heeft, ten heeft al niet konnen helpen, want hy die aan || niemandt, soo langh hy leefde, wilde openbaren.’

Uit de daarop volgende woorden blijkt, dat de trouwens zeer verschillende oplossing van van ceulen in het bezit van twilt is geweest.

‘Maar na sijn overlijden, soo is my die, beneffens de solutie van || Ludolf van Keulen, met groote vreught ter hand gekomen, die by || my ook, na den aard der Liefde, in geen kleender estime, als by de || voornoemde Twilt, gehouden is geweest, 't welk de Liefhebbers || ook uyt soo heerlijk Werk licht sullen kunnen bespeuren.’

4. Hierop volgt een twaalftal, ten deele verschillende ‘Analysen’ of ‘Solutien’: en daarop bladz.36-49 het overeen-komstige vraagstuk voor vier cuben. Ten slotte blz. 50 komen de twee brieven van ludolf van ceulen aan nicolaas huybertsz. van percijn; brieven van een ouderen geleerde, die zijnen jongeren vriend steunt en opwekt bij zijn wetenschappelijk streven. De eerste luidt aldus.

‘Wyse, Voorsichtige, Konst-rijcke, besondere goede Vriendt, UL. schrijven heb ik || gisteren ontfangen, soude terstont geantwoort hebben, ten ware dat de vermaninge || van de koorts 't mijn verhindert hadt, daar ik eensdeels mede gequelt was, het is nu re- || delijck, daarom ik dese voorgenomen heb te schrijven, het is my van herten lief dat UL. || hem soo oeffent in de heerlijkste Konsten van Meten en Stellen, vaart soo voort UL. gelij- || ken sal in weynigh jaren niet veel te vinden zijn, ik zal UL. soo veel my mogelijk behul- || pelijk wesen, ik sal geen Quaestien bekomen van anderen, dat my veel gebeurt, of ik sal || copye aan UL. over senden, soo verre UL. daar in dan swarigheyt vindt, beloove U te hel- || pen, dit sal UL. dienen tot geen geringe saak, soo veel aangaal de 57 en 69

Vrage in || mijn boek van de Cirkel, zijn sulks, dat die de 57 kan solveeren, die kan de andere mede || maken. Deze 57 Quaestie is konstigh, en wordt van veele onmogelijk geacht op te lossen, || daar ik UL. veel van seggen sal, als wy eenmaal t'samen komen, het is de 19 Quaestie || van 't vijfde Boek van Diophante van Alexandrie, maar niet gesolveert, alsoo doet mede || den gene die 't selve Boek uyt de Grieksche Spraek in 't Latijn heeft overgeset, ik hebbe die || een ander geleert die my daar van rijkelijk betaalt heeft, maar heeft sijn beloften niet ge- || houden, dat is, hy beloofde my die niemant te sullen leeren, soo lange myn groot werck || niet gedrukt was, daar in ik de Lief-hebbers de voornoemde Quaestie gesolveert voor-dra- || gen soude, maar heeft in tegendeel een wijl tijdts daar na de voornoemde Quaestie aan een || ander geleert, die hem daar na tegen alle waarheyt beroemde, de Solutie door sich selven || gevonden te hebben, wat arbeydt ik daar aan gedaan heb is Godt bekent, nochtans werd || ik gedwongen door de liefde en vriendtschap, die ik tot UL. drage, UL. te belooven de || geheele operatie sonder eenigh recompens te schikken, soudt nu gaarn gedaan hebben, indien || myn hooft beter gestelt waar geweest, het heeft veel moeyte en veel schrijvens in, daarom hope || ik soo 't Godt belieft in de Paessche Heylige Dagen my daar aan te maken, en aan UL. te || senden, ik soude nu garen voor UL. wat dichten, maar mijn hooft wilt nu niet lijden, || wenschende UL. met UL. Huys-vrouw en Familie, dat u saligh is. Met haast uyt Ley- || den, den 21 Maart, Anno 1610. || UL. Dienaar en Vriendt || ludolf van keulen.

Hier op volght na de tweede brief van dito van Keulen, || met de Solutie van voor-genoemde Quaestie.

Eersame, Voorsienige, Konst-rycke, besondere Vriendt, UL. schrijven is my ter- || stont behandight, daar uyt verstaan heb UL. aller gesontheyt, dat my lief is, ik met || mijn Familie zijn mede noch in goede doen, ik schik UL. hier het werk, waar door ik hier || dese konstage Vrage gevonden heb, en soo ver UL. daar swarigheyt in vindt, ik sal u als || myn Vriendt behulpelyk zijn schrijft mijn maar UL. begeerte: my is kortelingh uyt || Duytslandt wat gesonden, dat lustigh maar slecht is, soo UL. yets daar van begeert, || schrijft my, ik sal 't u over senden: ik soude UL. wel meer schrijven, maar heb voor te- || genwoordigh geen tijdt, hier mede wensch ik UL. met al

u geselschap het aldersaligliste. || Uyt Leyden, den 1 May. Anno 1610. || UL. Dienaar en Vriendt || ludolf van keulen.

Volght dan de 57 Quaestie met haar Solutie.---

Antwoordt || 494424 472696 448000/2352637.’

De oplossing, die hier volgt, is eene geheel andere, dan de boven geschetste; van ceulen eindigt haar met de woorden: ‘syn alsoo de getallen recht gevonden, daar van Godt alleen de eere toekomt.’

5. Uit de eerste brief blijkt vooreerst, dat ook ludolf van ceulen, zich, naar de gewoonte dier dagen, voor zijne oplossingen liet betalen.

Van meer gewicht is de vermelding van zijn groote werk,’ waarin hij ‘de voornoemde Quaestie gesolveert voor-dragen soude. Dit moest wel dezelfde arbeid zijn, waarvan van ceulen gewaagt in zijn voorbericht van zijn boek ‘Van den Circkel,’ [zie Bouwstoffen No. VIII, § 8.].

‘grooter werck/ daer inne onder andere ghehandelt sal || werden van den alder-constigsten Regel Cos/ met veel konstighe Exempels/ my van || veel Meesters deser konst te maken ghesonden/ met de beantwoordinghe/ en het gene || daer op ghemaeckt ende ghevonden is/ Met noch het noodt-wendighste der voornoem- || den Regel Cos/ welck ick tot Aernhem op 't Hoff van Gelderlandt Anno 1589 gevon- || den hebbe/ door de hulpe van Godt/’

Tot nog toe meende ik, dat dit werk van van ceulen was zijne ‘Arithmetische en Geometrische Fondamenten,’ die het eerst [zie Aanteekening 17 bij No. VIII der Bouwstoffen] door zijne weduwe adriana symons in het licht is gegeven. Immers worden in dat werk ook verschillende personen genoemd, die hem vraagstukken ter oplossing hadden toegezonden, zoo als

de Const-rijcke wel-gheleerde ende Sin-rijcke Mathematicus, Meester Symon Steuijn {bladz. 187, 211 (in 1582), blz. 136, in 1583)},
zijn Discipel Pieter Cornelisz. (blz. 163, 243),
de constighe Landmeter Adriaen Ockers van Amsteredam (blz. 196, 243) zijn leermeester,
de hervaren ende rechten liefhebber dezer Const, Meester Johan Pouvvels blz. 203, 212),
de constigen Jonckman Cornelis Pietersz van Alcmaer (blz. 212),
de Hooch-geleerde Heer Johannes Wilhelmi Velsius, Doctor binnen Lewarden, (blz. 229),
zijn discipel Willeboort Rudolfsz Snellius Soon (blz. 212, 230, 242),
zijn discipel Nathaniel Claessoon (blz. 242),
de geleerde ende zeer hervaren in dese Consten, Meester Nicolaes Pietersz van Deventer (blz. 244 in 1584),
de rechte Liefhebber Samuel Krop van Doevers (blz. 244 in 1599),

terwijl hij op blz. 225, nog een vraagstuk behandelt, ‘opentlijck aengeclampt den achtsten Junio tot Leyden Anno 1598.’

Maar in deze Fondamenten vond ik ons vraagstuk niet, en konde het ook daarin niet vinden, omdat het in geen der zes ‘Deelen’ paste. Nu weet men, dat deze ‘Fondamenten’ afbreken bij een voorstel 17 (blz. 271), waarbij wel eene figuur, maar geen antwoord of oplossing te vinden is. Het konde dus zijn, dat die ‘Fondamenten’ slechts een brokstuk was, niet verder door van ceulen bewerkt, en dientengevolge ook niet verder door zijne weduwe in het licht gegeven. Doch bij het omslaan van het blad viel mijn oog op de volgende zinsnede (blz. 269)

‘Ick vviste hier noch vvel veelderhande oorden te setten met ander stuc- || ken, maer tsal beter te passe comen in mijn Cosbouck, daer ick de vindinge || des Hooch-geleerden Adrianus Romanus sal stellen.’

Daaruit mag men dus besluiten, - afgescheiden van de vraag of ‘de Arithmetische en Geometrische Fondamenten’ een brokstuk zijn of niet, - dat er nog een ‘groot Werck over Cos’ door ludolf van ceulen geschreven is; dat dit boek in Mei 1610 niet gedrukt was; dat zijne weduwe het niet heeft uit-gegeven; en dat het dus meer dan waarschijnlijk bij het over-lijden van van ceulen niet genoegzaam voor de pers gereed was gemaakt.

6. Er blijft nog over om met een paar woorden den verzamelaar dirck de hollander te gedenken, die in het beschreven boekje voor ons heeft bewaard, wat eenig nieuw licht verspreidde over den arbeid en den geest van ludolf van ceulen.

Hij heeft zich nog verdienstelijk gemaakt door eene verbeterde uitgaaf te bezorgen van ‘de Cijfer-konst van david cock

van Enckhuysen.’ Ik bezit daarvan de vierde Druck van 16612) te Amsterdam, waarin dirck de hollander zich noemt: Italiaens Boeck-houder/ Reecken-meester ende Liefhebber der Wiskonst.’ Deze druk is uitgegeven door hendrik tjercksz de vries, Boekverkooper/ op de Zee-dijck/ over de Storm-steegh/ in de Chronijck van Frieslant,’; terwijl ik een ander exemplaar bezit, evenzeer ‘Den vierden Druck’, volkomen dezelfde als de bovengenoemde, maar in 16803) te Amsterdam uitgegeven door michiel de groot, Boeck-verkooper op de Nieuwen-dijck/ tusschen de twee Haarlemmer-Sluysen.’

Men zoude meenen, dat hier van eenige soort van nadruk sprake was; maar het werk van Dr. ledeboer4) lost de onzeker-heid volkomen op; daaruit blijkt toch dat de zaak van h.t. de vries slechts van 1652-1674 bestond, die van m. de groot 1660-1682; de laatste had dus denkelijk het copijrecht van den eersten overgenomen. En dit wordt verder bevestigd door eene ‘Sevende Druck van de Cijferkonst5) in 1734 te Amsterdam uitgekomen bij ‘de Erve van de Wed.: G. de Groot, Boekverkoopster op de Nieuwen Dijct, tusschen de twee Haarlemmer Sluysen.’ Volgens Dr. ledeboer toch komen te Amsterdam achtereenvolgens voor, in hetzelfde huis

Gysbert de Groot 1682-1696,
Weduwe G. de Groot 1696-1717.
Erven Wed. G. de Groot 1717-1653.

Uit de voorrede van het boekje van Noot (2) van hendrick de vries, blijkt, dat eerst deze vierde druck door de hollander is verbeterd en vermeerderd met een ‘Aenhanck van (80) diversche Questien (blz. 339-376).

Dat dit rekenboek van david cock van enckhuysen veel en lang is gebruikt, blijkt wel uit een ander boekje, ‘De vernieuwde Cyfferkonst door David Cock van Enchuysen, vermeerderd door J.B. Wappers,’6), dat te Gent is uitgekomen in het jaar 1799. Hier is echter de orde van de behandelde onderwerpen geheel veranderd.


Vorige Volgende