Journal tenu par Isaac Beeckman de 1604 à 1634. Tome 4: Supplément

[1618]

[14 maart 1618]

Les notes généalogiques dans le Journal portent à fol. 49recto:

Jacob, myn broeder, troude met Susanneken Adriaens van der Goes, den 12^en April an^o 1617⁴⁾, ende kreghen tsamen eenen sone, Adriaen genaemt, den 24^en Febru<arij> ten 4 uren snachs an^o 1618⁵⁾. Syn wyf is gestorven den 14^en Meerte ten 7 uren smergens 1618⁶⁾.

4) Cf. ci-avant p. 38.

5) Ce fils fut baptisé à Veere le 4 mars 1618 (témoins: Abraham Beeckman, Jacob van Rossen, Jacquemyntgen Adriaens et Susanna Willaerts (c'est à dire Suzanne Beeckman, soeur d'Isaac, cf. plus haut p. 31).

6) Elle mourut à cause des couches. C'était probablement à l'occasion de son enterrement à Veere que Beeckman dressa la note à la page 167 du t. I. - L'enfant mourut le 11 septembre 1618.

[18 maart 1618]

Registre des membres de l'Eglise réformée à Middelbourg, 1607-1621 (cf. plus haut p. 19).

Het 270^e Avontwael, ghehouden den 18^en Martij d'anno 1618.

Met attestatien:

.......................................

Florensken de Cerf, jougedochter^a); onderteekent Jac. Hondius⁷⁾, tot Vlissingen, 10 Maert 1618.

.......................................

Met belydenisse:

.......................................

Catelyntjen Cerfs, jongedochter^a), op de Nieuwe Haven, naest Yperen.

Avec ses compagnons de voyage - son oncle Jan Pieters van Rhee, et Hendrick Somer (cf. t. I, p. 218) - Beeckman se trouva à Caen le 7 août 1618 (cf. t. I, p. 208 et ci-

a) j.d.

7) Jacobus de Hond, fils du ministre Cornelis de Hond, était né dans le Palatinat. Devenu ministre à Flessingue en 1602, il se maria en 1604 à Middelbourg avec Elisabeth Schyn, jeune fille d'Anvers, et mourut à Flessingue en mars 1625.

a) j.d.

[p. 40]

⁺après p. 47) et le 18 août 1618 il subit l'examen pour le baccalauréat et le licentiat en médecine, nécessaire pour pouvoir passer au doctorat¹⁾.

+ 1618

1) Dans la pratique il n'y avait pas d'intervalle entre l'examen du baccalauréat et celui de la licence, les programmes étant les mêmes, mais la licence se distinguait par un appareil un peu plus solennel. Cette licence donnait au candidat le droit de pratiquer. C'était donc, au fond, le grade le plus important; une fois licencié, il ne dépendait plus que du candidat de devenir docteur. - Pour d'autres médecins qui ont étudié à Caen, cf. t. I, p. XI, n. 2.

[25 augustus 1618]

Registre de réception aux actes de la Faculté de droit à l'Université de Caen. - Caen, Bibliothèque municipale.

25 août 1618. - Honestus vir Joannes Petri van Rhee, inc. Amstelredami²⁾.

2) Jan Pietersz. van Rhee mourut à Amsterdam peut-être vers 1634 (cf. plus haut p. 36 n. 1), mais sans doute avant 1637, car lorsqu'on proclama à Middelbourg, le 2 novembre 1637, les bans entre sa fille Janneken et Petrus Durantius, ministre à Geertruidenberg, elle est dite être sans parents et tuteurs. Beeckman le désignera plus loin (p. 48) comme ‘Janoom’.

[6 september 1618]

D'après l'usanee adoptée en ce temps-là, Beeckman fit à l'occasion de sa promotion une leçon d'ouverture. C'était par elle que le candidat devait montrer son éloquence, pour répondre ensuite publiquement aux attaques des adversaires qu'on lui avait choisis et défendre ses thèses³⁾. Toute cette cérémonie se passa le 6 septembre 1610 (cf. t. I, pp. 215-216, 217 et 218). Le texte du discours a été écrit au fol. 285verso et 286recto du Journal par la main gothique du copiste dont Beeckman se servit vers 1626. Beeckman lui-même a écrit en marge: Medicina discursu a ine laudata autequam pro gradu disputarem.

Circumfertur sententia Platonis celeberrima, quâ dicit hominibus oculos esse datos ad caelum contemplandum. Cùm autem per caelum intelligat astra et eorum cursus, quis non videt potissimam partem totius universitatis hoc dicto comprehendisse? Sive enim incorruptibilitatem materiae caelestis spectes, sive motum stellarum infallibilem, ubique divinitati atque ipsi Deo occurres. Namque haec inferiora, quae et sublunaria dicuntur, perpetuis subijciuntur mutationibus: ignis aquae opponitur atque aqua ignem destruit, mutuumque exitium velut hostes infensissimi expetunt sibique invicem perpetuum bellum gerunt eademque omninò lege reliqua elementa, ex quibus omnia terrestria constant, feruntur et procedunt; at coelo pax aeterna nihilque alteri contrarietur tamque firmâ amicitiâ velut compagine caelestia omnia sibi invicem sunt alligata, ut Philosophus non parvâ quidem conjecturâ à caelo sumptâ, aeternitatem mundi adstruxerit.

Quid verò divinius revolutionibus erraticarum, nullis erroribus obnoxiarum? Quis harum motor? Quis author? Quis praeses? An non certissimis conclusionibus hoc pacto probamus naturam quandem intelligentem quae haec tam concinnè coaptavit? Non aliter quàm gubernatorem clavum in navi tenentem, certò intelligimus cùm navis rectâ ad portum dirigitur?

Quae quamquam ita se habeant, non tamen existimandum est cadum esse adaequatum objectum oculorum aut solis oculis id subijci. Infinita enim restant alia quibus percipiendis oculi inserviunt, omissis etiam ijs quae cum animalibus brutis communia habemus continetque caelum innumera quae oculis solis non cernuntur, sed ad horum comprehensionem mens divinitus nobis data, his utitur

3) Pour l'institut académique cf. H. Prentout, La Faculté de médecine de l'Université de Caen au XVI^e siècle (Bulletin de la Soc. des Antiquaires de Normandie, t. XXVI, 1909); pour les disputes et l'examen lui-même: Prentout, La vie de l'étudiant à Caen au XVI^e siècle (Mémoires de l'Acad. des sc., arts et belles letters de Caen, Caen, 1905, pp. 16-19).

[p. 41]

⁺ instrumentis. Mens igitus potior est pars nostri et quicquid in nobis lande dignum est, id sibi vendicat. Huic subijcitur non modo caelum eaque quae oculis videntur, verùm omnia invisibilia et visibilia, omnia divina et humana, et quicquid rationem essentiae habet id omne intellectus versat, penetrat penitusque ingreditur. Mentis pars una versatur circa res divinas hasque simpliciter credit iisque assentitur, non quia eas intelligit, sed ob instinctum aliquem supematuralem, quae pars forsitan non ineptè conscientia vocabitur.

Huic è directo opposita est scientia quae ratione constat atque ei tota philosophia subijcitur, ita ut philosophia sit adaequatum objectum rationis. Nullum enim statutum, nullum praeceptum, nulla regula in philosophiâ admittenda quae non sit apodicticâ et certissimâ ratione comprobata et intellectui tam apertè et nudè objecta atque visibilia oculis obijciuntur.

Dividitur philosophia in duas partes: mathematicam et physicam. Physica circa ipsas res corporeas, mathematica verò circa earum quantitatem versatur, tantòque major est physicae dignitas quantò umbra ignobilior ipso corpore. Est tamen ad physicam cognitionem consequendam tanta mathematicae necessitas ut aptissimè ejus manûs vocari possit, qua solâ quicquid physica continet, apprehenditur; ideòque Graecis philosophis à μανθάνω dicta est, quia nemo physicae initiabatur qui mathematicarum artium disciplina aditum legitimum ad physicam sibi non parasset praefixumque erat scholis physicis: οὐδείς ἀγεωμετρητὸς εἰσιτω.

Physica est corporum naturalium | scientia scrutaturque naturas caeli et terrae et omnium quae in ipsis continentur^a). Horum praecipuum est homo, imò verò altera pars universi. Dictus enim est μικροκοσμὸς, quia omnia continet quae μακροκοσμὸς, sed subtiliori essentiâ praedita cùmque subtiliora rudioribus sint cognitione posteriora exacta μικροκόσμου scientia habere non poterit nisi qui naturam macrocosmi perfectè habeat exploratam; utque Colossus fuit regula omnibus pictoribus et lapicidis (quod etiam ad humanam figuram pertinebat), sic physica ea quae macrocosmum tractat, prior est regula ejus artis quae hominis et microcosmi naturas perscrutatur. Haec ars medicina dicitur, artium omnium ultima et praestantissima, ipsique artifici utilissima et maximè necessaria. Quid enim anatomiâ proprij^b) corporis jucundiùs? Quid sui ipsius^c) cognitione pulchriùs? De caelo descendit γνῶθι σεαυτὸν, inquit Juvenalis¹⁾. Utilitatem verò et necessitatem satis declarant morbi nisi eum medicinae ope ab illis artifex praeservetur, nisi ab illis jam obsessus liberetur.

Actum est de astrorum cognitione, de geometriâ, de physicâ omninòque tota mens, licet doctissima antiquosque philosophos aequet scientiâ, uno momento peribit. Excolamus igitur medicinam, ut reliquas scientias tuto liceat colere, et incumbamus medicinae, quae nos ad reliques artes liberè exercendas aptos et idoneos reddit.

+ 6 septembre 1618

a) continenturi.

b) propri.

c) suipsius.

1) Lib. IV. Sat. XI, 1. 27.

[p. 42]

⁺

Ut autem huic discursui finis debitus imponatur, exercendos nos potissimus duximus in eâ parte medicinae, quae de febribus tractat. Est enim febris morbus maximus et frequentissimus, ita ut pervulgatum sit neminem sine febre mori. Inter febres verò tertiana intermittens^a) regula morborum acutorum, qui opem medicinam praecipuè requirunt, ideoque de hac exquisitâ praesens hoc exercitium nobis inchoatum est et dante Deo cum fructu finietur.

Nous reproduisons ici les thèses que Beeckman soutint à Caen d'après le seul exemplaire connu du British Museum à Londres (côté 1179, d 9 (3). C'est peut-être un exemplaire conservé par Beeckman lui-même, puisque les deux lignes ajoutées à la dernière page semblent de la même main gothique qui écrivit aussi la note de la page 200-201 du t. I qui s'y rapporte. - Au litre n'a pas été ajoutée la date de sa promotion, mais nous savons par le Journal lui-même (cf. t. I, pp. 215, 217 et 218) qu'elle fut celle du 6 septembre. Les circonstances d'après guerre nous ont empêchè de faire des recherches ultérieures pour un exemplaire plus complet.

+ 6 septembre 1618

a) in mittens.

[p. 43]

⁺

Après cette deuxième page manquent les pages numerotées 3, 4, 5 et 6 qui constituaient apparemment les deux feuillets intérieurs du placard.

+ 6 septembre 1618

[p. 44]

⁺

Pour les Corollaria cf. t. I, pp. 200-201 et pour les lignes manuscrites cf. t. I; pp. 92-93, 252 et t. II, pp. 232, 288 et 302.

+ 6 septembre 1618

[p. 45]

⁺

Journal, fol. 287recto. - Ecriture de la main gothique vers 1626.

Argumentum Domini De Vandes¹⁾ contra quartum Corollarium²⁾ in Scholâ publicâ:

Quod quiescit, non movetur; lapis in manu existens, quiescit; ergo lapis in manu existens, non movetur.

Negabam minorem, quia cum manu movetur. Probabat:

Quod non mutatur loco, quiescit; lapis in manu existens, non mutatur loco; ergo lapis in manu quiescit.

Respondi ad minorem locum sumi dupliciter: pro superficie corporis continentis, et pro spacio diverso respectu universitatis. Si sumatur ‘locus’ priore significatione, major est falsa; si secundâ, minor.

Accepit responsionem³⁾.

+ 6 septembre 1618

1) Pour Denys Porée de Vandes, cf. t. I, p. 215, n. 3.

2) Pour ces Corollaria, cf. la page précédente, et pour la question de la ‘vis impressa’, t. I, pp. 24-25.

3) Après les diverses cérémonies qui accompagnaient la promotion, le candidat demanda à son maître ou parrain, les attributs du doctorat. ‘Et ausdites facultez’ (droits, médecine et arts) disent les statuts, ‘les docteurs catedrans qui creent le docteur .... le decorent et donnent la robe de escarlatte, le livre, le signet, la ceinture et le bonnet et le bayser’. Cf H. Prentout, La vie de l'étudiant à Caen au XVI^e siècle, p. 23, où l'on trouve exposé ensuite la signification de ces attributs. Les ayant reçus et le serment prêté, le nouveau docteur sortit accompagné du docteur-parrain et souvent aussi des autres docteurs et des écoliers. A ce sujet cf. t. I, pp. 215-216.

Denys Porée de Vandes, à Gabriel Morice⁴⁾, à Caen.
6 septembre 1618

Journal, fol. 287recto. - En tête: Copie van den brieff, die Mons^r De Vandes schreef aen Maurice, oock professoor in de medicine⁵⁾.

Monsieur Maurice,

Je vous prie de signer les lettres⁶⁾ de Sieur Beeckman. Je l'ay ce jourdui mené aux escoles publiques de l'université⁷⁾, où il a doctement et elegantement respondu. Il est sçavant en la langue grecque et outre la medicine et la philosophie, il sçait aussi les mathematiques. Je croy qu'il fera honneur à nostre Faculté et Université. A mon retour de Roan, je ne vous oblyeray....⁸⁾.

Le sixieme jour de Septemb., mil six cent dix huit.

Vostre bien affectioné

....⁹⁾ DE VANDES.

4) Gabriel Morice de Saint-Silvain, était devenu bachelier à Caen en avril 1611, licencié en novembre 1612, régent en 1614 et docteur en médecine en 1615. Il était reçu docteur-régent le 2 mars 1618, précisément par Denys Porée de Vandes. Il devint aussi doyen en 1624-1625, mais en 1626, comme son tour était venu de le redevenir, on s'y opposa en raison de sa religion: il était protestant, comme aussi peut-être De Vandes.

5) Plus tard Beeckman a écrit en marge: Litterae de Mons^r de Vandes ad Mons^r Maurice de me.

6) Le document suivant.

7) Cf. la fin de la note 3 de cette page.

8) Au lieu des points, le ms porte: ‘de reste en conde ick niet lesen’.

9) Au lieu des points le ms porte: ‘frater (denck ick)’.

[p. 46]

⁺

(het opschrift was:)^a)

A Monsieur

S^r Gabriel Maurice^b), lorsqu'il sera au retour de Fallaese, ou de sa maison de Sainct-Silvin.

Journal, fol. 286verso. - Copie de la main gothique vers 1626. Nous reproduisons cette copie sous la forme (lettres capitales etc.) alors en usage pour les bulles universitaires)¹⁾.

Universis praesentes literas inspecturis Nobilis vir Dionysius de Wandes medicus Regius, Decanus etc. celeberrima Medicinae Facultas almae Universitatis Cadomensis Salutem in Christo Jesu.

Cùm in omnium Christianorum mente, Medicorum verò maxime, Dei optimi maximi cognitio et motus versetur, aequum est ut hi nemini plus necessitudine aut gratiâ minusve odio aut ostensione tribuant quàm et res et veritas ipsa concesserit. Quando ergo non solùm communi famâ constantique omnium sermone, sed varijs etiam periculis et experimentis certiores facti sumus Magistrum²⁾ Isack Beeckman, Mittelburgo-Zelandum, cum moribus tum doctrinae studijs et testimonijs doctissimorum virorum, nobis longè esse commendatissimum, ne quâ in re eum laboris mercede et ingenij laude fraudaremus, hoc voluimus ejus in Medica studia meritorum testimonium esse sempiternum.

Illud igitur non hoc tantùm nostrum tempus aetatis, sed omnis posteritas intelligat, eum ipsum Magistrum Isack Beeckman, non ita pridem acerrimis examinibus tentatum, mox publicâ disputatione periclitatum, hodiè amplissimi doctoratûs insignia cum summâ docendae faciendaeque Medicinae publicè et privatim hîc et ubique terrarum³⁾ potestate, suo merito nostro decreto esse consequutum.

Quod quia ratum ac firmum facturum esse volumus, hanc tabulam, uno et altero nostrae Facultatis sigillo⁴⁾, nostris et Notarij nostri chirographis obsignatam, bonae nostrae ac perpetuae de eo opinionis indicem, Ipsi eidem nostrâ omnium voluntate concessimus.

Datum Cadomij, die sextâ mensis Septembris Anni Dominj Millesimi sexcentesimi decimi octavi.

DE WANDES

1618

G. MORICE⁵⁾

+ 6 septembre 1618

a) pas de parenthèses.

b) Maurice Morin.

1) Plus tard Beeckman écrivit en marge: Promotionis meae testimonium.

2) Pour la réception de Beeckman à la maîtrise, cf. t. I, p. 215-216.

3) Pour cet ‘ubique terrarum’, cf. t. I, pp. 216 et 218.

4) Les bulles, écrites sur parchemin, étaient pliées d'ordinaire du côté inférieur. Par un trou, on fit passer un ruban avec le sceau en cire. Ce sceau manque à notre copie.

5) Pour lui cf. ci-dessus p. 45, n. 4.

[p. 47]

⁺

Matrologe de la Faculté de Médecine de l'Université de Caen, 1506-1708; Caen, Archives départementales du Calvados, ms 453, fol. 159.

Isaacus Beeckman, Mittelburgo-Zelandus, Graecarum litterarum peritissimus, post disputationem solemnem de Febre tertianâ in publicis scholis habitam, suâ ita postulante scientiâ et experientiâ, Doctor medicinae factus est die sextâ Septembris anni 1618.

DE WANDES G. MORITIUS DE BRIX¹⁾.

Le document suivant relatant les dépenses de Beeckman pendant son voyage à Caen, sa promotion et son retour, se trouve au milieu des notes ordinaires du Journal à fol. 88recto-88verso (cf. t. I, pp. XXXIX, sub d) et 213, n. 1). Il est écrit en caractères courants, peut-être de la main de Beeckman lui-même, mais les lignes dernières sont mises en écriture gothique et probablement ajoutées (1626) à la place restée d'abord en blanc.

Aen Hoevereyn in de herberghe gegeven voor logys van Dynsdaechs tot Saterdaechs²⁾ effen 8 gulden.

Voor den professoor Maurice³⁾ een collation⁴⁾ betaelt van 22 stuyvers.

Denselven professoor eens te gast gehad, twelc my mynen weert te rekeninge brengen sal

Ic ben den 11^en Augusti tot Columbels in de kost gecomen.

Eenighe onnoodighe kleyne collations gehad om den schipper te gelieven ende andersins tot den 18^en Augusti, twelc een gulden ⁺twee oft drie mach beloopen.

Den 18^en Augusti gaf ic drie croonen in specie aen M^r De Wandes⁵⁾, professoor in de medicinen, eer hy my examineren wilde⁶⁾ ende wiert terstont van hem ende Io. Bryce⁷⁾ geexami-

+ 6 septembre 1618

1) Joannes de Brix ou Brixeius était en 1616 professeur royal de philosophie et recteur de l'Université quand il fut reçu bachelier en médecine. Il passa sa licence en mars 1617 et son doctorat en décembre 1617. En 1618 il était docteur-regent.

2) Probablement le 7-11 août 1618, puisque l'auteur changea le 11 août de demeure.

3) Gabriel Morice; cf. ci-dessus p. 45, n. 4.

4) C'était une coutume obligée de donner avant le baccalauréat un dîner ou une collation au recteur, à ses professeurs et au bedeau. De telles collations se répétaient au cours des cérémonies.

+ Myn promotie te Caen.

5) Denys Poree de Vandes, cf. ci-dessus p. 45, n. 1.

6) Coutume égal ment obligée.

7) Jean de Brix; cf. ci-dessus n. 1. Le ms porte: ende Cobryce. Le copiste semble s'être trompé en pensant peut-être à la famille middelbourgeoise Cobryce ou Cobrysse, dont Guillaume (né à Dover) fut depuis 1615 le mari de Anna van Ryckegem, soeur ainée de Janneken, qui deviendra bientôt la seconde femme de Jacob Beeckman. Cf. plus loin pp. 58 et 210.

[p. 48]

⁺neert ende bequaem verclaert tot het baccalaureaatschap ende licentiaetschap. Ende wiert geoordineert, dat ic publice examineren soude, twelck ic aennam¹⁾. Ende nae het dispuut beloofden sy my doctoor te maecken.

Paulus Jansen²⁾ gegeven voor vracht 3 croonen³⁾.

Aen syn knechten omt goet tuys te bringen 15 stuyvers.

Voor myn theses te drucken 2 croonen.

Voor 22 te binden 16 stuyvers.

Voor myn promotie 100 gulden gegeven den 5^en September⁴⁾

Aen de knechten ende den bedel, diet ooc onderteekende, wel 1½ croon, den 6^en September.

Voort bleck, parckement, etc. was, lint wel 1 croon.

Aen Janoom⁵⁾ geleent, als hy syn promotie nam te Caen int leste van October 25 gulden.

Den 8^en September gecocht 2 paer handschoenen⁶⁾ voor 43 stuyvers.

Aen myn huyswaert te Caen voor een maent kost 6 croonen.

De vrouwe metten kinders 1 croon.

Voor Mauricen⁷⁾ 25 stuyvers⁸⁾.

+ septembre 1618

1) L'examen pouvait être ‘privé’ ou ‘rigoureux’ (public).

2) Sur ce capitaine de vaisseau, cf. t. I, p. 208.

3) Le ‘croon’ valait alors 2 florins.

4) Déjà Ramus, en faisant très minutieusement, article par article, le compte des frais qui accompagnaient la prise des grades universitaires, s'y était vivement opposé, la plupart étant exigées pour une multitude de formalités: (Proaemium reformandae Parisiensis Academiae, ad Regem, 1562 ou en même temps: Advestissements sur la réformation de l'Université de Paris, au Roy). On voit qu'à l'époque de Beeckman, les circonstances étaient peu changées.

5) Jan Pietersz. van Rhee. Cf. ci-dessus pp. 36 et 40.

6) Cet achat était probablement une conséquence de la coutume, ou obligation, de donner des gants aux professeurs qui avaient assisté à la promotion. Mais, s'écrie Ramus dans son opuscule cité, ‘quel argument suffisant ont les gantz, les bonnetz, les banquetz, pour prouver la diligence et suffisance du disciple?’

7) Gabriel Morice; cf. ci-dessus p. 45, n. 4.

8) Renvoyons, à l'occasion de cette dernière mention des relations de Beeckman avec l'Université, encore deux études qui complètent celles citées au t. I, pp. 208, n. 3, 215, n. 3 et ci-dessus p. 40: H. Prentout, L'université de Caen à la fin du XVI^e siècle (Caen, 1908) et Id., 1432-1932, L'université de Caen, son passéson présent (Imprimerie arti stique Malherbe de Caen, 1932), où il y a parlé de Beeckman aux pp. 130 sqq.

[p. 49]

⁺

Noch aen myn weert twee gulden.

Voor myn schoenen te lappen 12 stuyvers.

Met Henrick¹⁾ ende Caspaer²⁾ 3 dagen gereden. 'Sdaechs voor de peerden ende den knecht 24 stuyvers. Voor eten, wyn van den knecht ende het peerdt in de 3 daghen ben ick vergeten.

Den 15^en September gingen wy weer naer Caen ende dien dach ginck ick na Haber ende quam 's avonts weer.

'S anderdaechs, Sondach synde, ginck ic over (sic)³⁾ tot Justinus⁴⁾; koste 36 stuyvers.

Den 19^en was ick met de Justinussen⁵⁾ te Haber⁶⁾; hadde my gekost 2 gulden 9 stuyvers.

A une de ses rencontres, en novembre ou en décembre 1618, à Breda avec Descartes, Beeckman proposa à son nouvel ami la question si l'on pouvait savoir combien d'espace une pierre tombant parcourrait pendant une heure, si l'on savait combien d'espace elle parcourt en deux heures. Le résultat obtenu par Descartes nous est connu non seulement par ses notes (t. I, pp. 360-361), mais aussi par le document suivant qu'il remit à Beeckman. Celui-ci le fit copier, vers 1628, par le copiste de la main gothique, et il occupe actuellement fol. 162recto-162verso du Journal. Il est précédé d'un autre écrit de Descartes sur le paradoxe hydrostatique et datant de la même époque, mais il semble bien résulter des notes de Descartes (t. I, pp. 360 et 364) que le présent document est le premier en ordre de date. Ajoutons que le document et la ‘démonstration triangulaire’ qu'il comprend, semblent avoir été en possession de Beeckman, lorsqu'il dressa ses propres études exactes sur le sujet (t. I, pp. 260-264).⁷⁾

In propositâ quaestione⁸⁾, ubi imaginatur singulis temporibus novam addi

+ septembre-novembre ou décembre 1618

1) Sans doute le Hendrick Somer, mentionné au t. I, p. 218, n. 6.

2) Il semble douteux qu'il s'agisse de Caspar Adriaensz. Parduyn, baptisé à Middelbourg le 2 novembre 1594, issu d'une famille distinguée, car, après avoir étudié en théologie à Leyde (immatriculé le 19 février 1620), le magistrat de Middelbourg n'augmenta sa subvention, pour aller étudier en France, que le 1^er mai 1621. Sur lui plus loin p. 347. Caspar van Baerle qui prit ses grades de docteur en médecine à Caen en 1620, semble également exclu.

3) Lisez: ‘over de Seine’, ou ‘over met het schip’, mais peut-être la place vide est superflue.

4) Probablement Justinus van Assche, venu tout récemment de Londres et se rendant à Saumur (cf. t. I, p. 219, n. 2 et plus haut pp. 38 et 39(nn)). La note suivante nous apprend cependant qu'il y avait deux étudiants du même prénom.

5) Le compagnon de voyage de Van Assche, Justinus Arondeaux (cf. sur lui t. I, pp. I, V, XI et 219 (n) et plus haut pp. 31 et 38), s'arrêta à Caen environ neuf mois, se trouva le 22 juin 1619 à Pont-Audemer, et présenta son attestation de foi, datée de Caen le 5 juin 1619 et signée par Daniel Massis, à son rentrée à Veere en février 1620. Ayant fait des études en droit, il devint à Veere, en novembre 1623, receveur de contributions, mais le 24 janvier 1625 il prêta le serment civique à Flessingue, où il fut créé notaire le 19 mars 1625.

6) Beeckman se trouvait encore au Hâvre le 20 septembre 1618 (cf. t. I, p. 219).

7) A propos du sujet cf. la belle étude de M. Koyré citée déjà (avec d'autres) au t. I, p. XXXIII, n. 8, mais rééditée depuis sous le titre: La loi de la chûte des corps: Descartes et Galilée (Paris, 1939), où le document suivant est discuté particulièrement aux pages 36-40.

8) Beeckman écrivit plus tard en marge: Lapis in vacuo versus Terrae centrum cadens, quantum singulis momentis motu crescat, ratio Des Cartes.

[p. 50]

⁺ vim quâ corpus grave tendat deorsum¹⁾, dico vim illam eodem pacto augeri, quo augentur lineae transversae de, fg, hi, et aliae infinitae transversae, quae inter



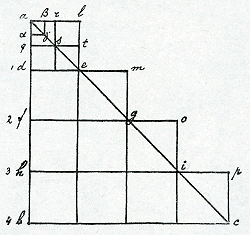illas possunt imaginari.

Quod ut demonstrem, assumam pro primo^a) minimo vel puncto motûs, quod causatur à primâ quae imaginari potest attractivâ vi Terrae, quadratum alde²⁾. Pro secundo^b) minimo motûs, habebimus duplum, nempe dmgf: pergit enim ea vis quae erat in primo minimo, et alia nova accedit illi aequalis. Item in tertio minimo motûs erunt tres vires, nempe primi, secundi et tertij minimi temporis, etc. Hic autem numerus est triangularis, ut aliàs fortè fusiùs explicabo, et apparet hunc^d) figuram triangularem abc repraesentare.

Immò, inquies, sunt partes protuberantes ale, emg, goi, etc., quae extra trianguli figuram exeunt; ergo figurâ trianguli illa progressio non debet explicari.

Sed respondeo illas partes protuberantes oriri ex eo quòd latitudinem dederimus minimis, quae indivisibilia debent imaginari et nullis partibus constantia. Quod ita demonstratur:

Dividam illud minimum ad in duo aequalia in q; jamque arsq est <primum>^e) minimum motûs, et qted secundum minimum motûs, in quo erunt^f) duo minima virium. Eodem pacto dividamus df, fh, etc. Tunc habebimus partes protuberantes ars, ste, etc.^g). Minores^h) sunt parte protuberante ale, ut patet. Rursum, si pro minimo assumam minorem, ut aα, partes protuberantes erunt adhuc minores, ut αβγⁱ⁾, etc. Quòd si denique pro illo minimo assumam verum minimum, nempe punctum, tum illae partes protuberantes nullae erunt, quia non possunt esse totum ^c)

+ novembre ou décembre 1618

1) Au lieu du principe de la conservation du mouvement et celui de la superposition des vitesses antérieurement acquises qui produisent l'accélération (principes que Beeckman avait communiqués à Descartes (cf. t. I, pp. 44, 174 et 261)), celui-ci part de l'idée que c'est la force qui se conserve pendant la chùte et que cette force est à chaque moment proportionnelle à la vitesse. Cf. ses notes au t. I, pp. 360-361.

a) 1^o pro.

2) Contrairement au graphique de Beeckman (t. I, p. 262), Descartes représente sur l'axe vertical les chemins parcourus, tandis que les superficies représentent la somme des vitesses moyennes.

b) 2^o.

d) hic.

e) primum omis.

f) erant.

g) sit e etc.

h) minores res.

i) αβe.

c) comme le copiste a mal representé la figure du t. I, p. 262, il a mal copié aussi la figure présente: la ligne ac, au lieu d'être droite, est brisée en e, au dessous de dem les carrés sont devenus des rectangles, et les distances ad, df, fh et hb sont fort inégales. Les chiffres 1, 2, 3 et 4 sont écrits respectivement devant α, d, f et h et au lieu des lettres γ et s le copiste a mis o et g.

[p. 51]

⁺ punctum, ut patet, sed tantùm media pars minimi alde; atqui puncti media pars nulla est.

Ex quibus patet, si imaginetur, verbi gratiâ, lapis ex a ad b trahi a Terrâ in vacuo per vim quae aequaliter ab illâ semper fluat, priori remanente, motum primum in a se habere ad ultimum qui^a) est in b, ut punctum a se habet ad lineam bc; mediam verò partem gb triplò celeriùs pertransiri a lapide quàm alia media pars ag, quia triplo majori vi a Terrâ trahitur: spatium enim fgbc triplum est spatij afg, ut facile probatur. Et sic proportione dicendum de caeteris partibus¹⁾.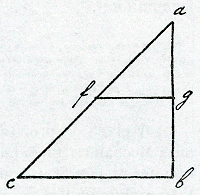

Aliter verò potest haec quaestio proponi difficiliùs hoc pacto²⁾:

Imaginetur lapis in puncto a manere, spatium inter a et b vacuum. Jamque primùm, verbi gratiâ hodiè horâ nonâ^b), Deus creet in b vim attractivam lapidis, et singulis postea momentis novam et novam vim creet, quae aequalis sit illi quam primo^c) momento creavit³⁾. Quae juncta cum vi antè creatâ fortiùs lapidem trahat et fortiùs iterum, quia in vacuo quod semel motum est, semper movetur⁴⁾. Tandemque lapis, qui erat in a, perveniet ad b hodiè horâ decimâ^d).

Si petatur quanto tempore primam mediam partem spatij confecerit, nempe ag, et quanto reliquam^e), respondeo lapidem descendisse per lineam ag⁵⁾ tempore ⅞^f) horae, per spatium autem gb ⅛^g) horae. Tunc enim debet fieri pyramis supra basim triangularem, cujus altitudo sit ab, quae quocunque pacto dividatur unâ cum totâ pyramide per lineas transversas aequo distantes ab horizonte. Tantò celeriùs lapis inferiores partes linae ab percurret, quantò majoribus insunt totius pyramidis sectionibus⁶⁾.

Aliter denique proponi potest de reditu redituum⁷⁾. Qui si singulis momentis augeri imaginetur, et quaeratur quid^h) hoc vel illo tempore debeatur, solvetur haec quaestio etiam proportionibus ductis à triangulo. Sed dividi non debet linea ab in partes arithmeticas, hoc est aequales, sed in geometricas, sive proportionales.

+ novembre ou décembre 1618

a) quod.

1) Descartes repétera ce résultat faux, où la vitesse du mobile est une fonction, non du temps écoulé (comme l'admettait Beeckman), mais de l'espace parcouru, dans ses notes contemporaines (t. I, p. 361) et dans ses lettres du 13 novembre et du 18 décembre 1629 (cf. plus loin pp. 166-167 et 170-171). C'est au dernier endroit qu'il assure (d'après Beeckman?) que chaque boule, de quelle matière qu'elle pût être, obéit à la loi supposée. Cf. ci-après p. 170 avec la note 6.

2) Descartes suppose le cas où la force attractive croîtrait d'instant en instant. Il a resumé cette digression dans ses notes contemporaines (t. I, p. 361).

b) 9.

c) 1^o.

3) Cf. ci-dessus p. 50, n. 1.

4) Sur ce principe, connu de Beeckman depuis longtemps, et que Descartes admet cette fois, cf. t. I, p. 263.

d) 10^a.

e) reliquum.

5) Ligne qui représente, comme toujours chez Descartes, la trajectoire.

f) ⅛.

g) ⅞.

6) C'est à dire les vitesses croîtraient comme les cubes et non plus comme les carrés.

7) Cf. t. I, p. 362.

h) quod.

[p. 52]

⁺ Quae omnia evidentissimè ex meâ Algebrâ geometricâ possem probare, sed nimis longum foret.

Pendant leurs entretiens, Beeckman proposa encore à Descartes de démontrer le paradoxe hydrostatique, déjà esposé par Stevin¹⁾, et mentionné par Beeckman auparavant (t. I, pp. 48, n. 1, 73, n. 2 et 108). L'écrit présent était le résultat de ce défi, mentionné aussi dans la dernière des notes de Descartes (t. I, p. 364). Beeckman relève le document dans une note de juin 1619 (t. I, p. 306), mais il ne le fit copier que vers 1628 par le même copiste qui écrivit le document précédent; sous cette forme il occupe dans son Journal fol. 160verso-162recto (cf. t. I, p. XXXIX).

Ut²⁾ planè de propositis quaestionibus meam mentem exponerem, multa ex meis Mechanicae fundamentis essent praemittenda, quod, quia tempus non sinit, breviter ut jam licet, conabor explicare.

Et primò quidem, ex varijs gravitandi modis, quos jam omnes enumerare non opus est nobis^a), duo varij hîc distinguendi sunt, nempe quomodo aqua, in vase exist ens, ejusdem vasis fundum premat^b), et quomodo totum ipsum vas simul cum aquâ quae in ipso est, gravitet. Duo enim illa planè distincta sunt, ita ut unum altero plus vel minùs gravitare posse certum sit.

Secundò, ut quid significet verbum gravitare intelligatur, fingendum est corpus quod gravitare dicitur deorsum moveri, et illud in primo instanti motûs considerandum est^c). Vis enim quâ in primo instanti impellitur motus, ea est quae gravitatio^d) vocatur, non illa quae illud in toto motu fert deorsum, quae à prima valde distincta esse potest. Dicemus igitur gravitationem esse vim quâ proxima superficies corpori gravi subjecta, ab eodem premitur.

Tertiò, in illo motûs principio imaginabili, notandum etiam initium imaginabile celeritatis, quâ partes corporis gravitantis descendent^e); haec enim non minùs confert ad gravitationem quàm corporis ipsius quantitas. Verbi gratiâ, si una^f) aquae atomus descensura^g) sit duplò celeriùs quàm duo aliae^h) atomi, illa solaⁱ⁾ aequè gravitabit atque duo aliae^k).

Quibus praemissis, sint quatuor vasa ejusdem latitudinis in fundo, ejusdem ponderis si vacua^l) sint, et ejusdem altitudinis. Non infundatur in A plus aquae quàm B potest continere; relique tria^m) impleantur quantum possunt.

<Primo>ⁿ⁾, aqua unâ cum vase A aequè gravitabit atque aqua simul cum vase B.

Secundò, aqua sola in fundo vasis B aeque gravitabit atque aqua sola in fundo vasis D, et per consequens, magis quàm aqua in fundo vasis A; aeque item atque aqua in fundo vasis C.

+ novembre ou décembre 1618

1) Cf. t. I, pp. 73, n. 2 et 364, n. 1.

2) Au dessus du document est écrit en main du copiste: ‘René du Peron (sic) mihi’ et en marge, de la main de Beeckman: ‘Aquae comprimentis in vase ratio reddita a D. Des Cartes’.

a) nostrae.

b) premit.

c) le ms porte: motus considerare.

d) gravatio.

e) discendent.

f) anus.

g) descensurus.

h) alij.

i) ille solus.

k) alij.

l) vacui.

m) 3^a.

n) primo omis.

[p. 53]

<sup>+



a)</sup>

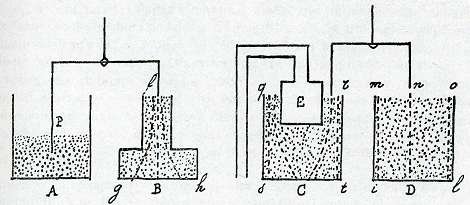Tertiò, D, totum vas et aqua simul, non magis nec minùs^b) gravitat quàm C, totum etiam, in quo embolus E firmus est.

Quartò, illud C totum magis gravitat quàm B totum. Ubi heri hallucinabar¹⁾.

Prior pars per se nota est.

Secunda ita demonstratur: Aqua in utroque vase aequali vi premit fundum vasis; ergo aequaliter gravitat. Probatur antecedens hoc pacto: tantum aquae incumbit supra omnia puncta determinabilia in fundo unius quàm in fundo alterius; ergo aequali vi premuntur. Verbi gratiâ, in fundo unius determinentur puncta g, B, h, in alterius i, D, l; dico omnia illa puncta aequali vi premi, quia scilicet premuntur lineis aquae imaginabilibus ejusdem longitudinis, nempe a supremâ parte vasis ad imam. Neque enim fg linea hîc longior censenda est quàm fB vel aliae: non premit enim punctum g ijs partibus quibus curva est et longior, sed ijs tantùm quibus deorsum tendit, quibus aequalis est alijs omnibus. Probandum autem est solum punctum f aequali vi premere tria puncta g, B, h atque tria distincta m, n, o premunt alia tria i, D, l^c). Quod fit hoc syllogismo:

Res graves aequali vi premunt omnia circumquaque corpora, quibus expulsis aeque facilè inferiorem locum occuparent;

Atqui solum punctum f aeque facilè occuparet inferiorem locum, si posset expellere tria puncta g, B, h^d) atque tria puncta, m, n, o, si expellerent alia tria puncta i, D, l;

Ergo solum punctum f aequali vi premit tria simul puncta g, B, h^d) atque tria puncta distincta, m, n, o premunt alia tria i, D, l.

Major videtur esse tam clara et evidens ut possit esse principium scientificum. Minor ulteriùs probatur: Imaginentur omnia inferiora puncta g, B, h et i, D, l eodem momento aperiri vi gravitationis corporum suprapositorum, certè

+ novembre ou décembre 1618

a) le vase C porte un g au lieu de s.

b) nec minus P.

1) Renvoi à des entretiens de la veille, comme ci-après p. 55 à ceux de l'avant-veille.

c) i, B, l.

d) g, b, h.

[p. 54]

⁺ eodem instanti concipiendum erit solum punctum f triplò celeriùs moveri quàm unumquodque ex punctis m, n, o. Illi enim tria eodem momento loca erunt explenda, quo momento unum tantùm cuilibet ex punctis m, n, o erit occupandum. Ergo vis quâ solum punctum f premit inferiora, aequalis est vi trium simul punctorum m, n, o. Eodemque modo probari potest de omnibus alijs punctis imaginabilibus in fundo vasis B, aequaliter <ea premi>^a) a superiore parum aquae, quae est in f, atque omnes partes fundi vasis D premuntur ab omni aquâ incumbente. Ideòque aequali vi fundum vasis B premi ab aquâ incumbente atque fundum vasis D. Quod erat probandum.

Una tamen objectio proponi potest, meo judicio non contemnenda, et cujus solutio superiora confirmabit. Quae tamen omnia corpora aequalis magnitudinis et gravitatis, si deorsum ferantur, habent certum quemdam aequalem celeritatis modum, quem non excedunt, nisi ab aliquâ vi extraneâ impellantur. Ergo malè assumitur in superioribus punctum f propendere ut triplò celeriùs moveatur quàm unum quodlibet ex punctis m, n, o, cùm a nullâ vi externâ dici possit illud impelli. Absurdum enim foret dicere illud^b) ab inferioribus aquae partibus attrahi, quod tamen mihi nuper valdè erroneè et non opinanter^c) ex ore elapsum est¹⁾; hîc enim consideramus illud, ut caetera corpora premit, non ut ab alijs impellitur vel attrahitur.

Ita tamen ad objectionem respondeo: Antecedens est verissimum; falsò autem ex eo deducitur punctum f non posse ad triplicem celeritatem propendere. Duo enim diversa sunt in ratione ponderum et valdè distinguenda, nempe propensionem ad motum et motum ipsum. In propensione enim ad motum, nulla habenda est ratio celeritatis, sed tantùm in motu ipso. Corpora enim quae deorsum tendunt, non propendent ut hac vel illâ celeritate ad inferiorem locum moveautur, sed ut quàm citissimè potest, eo perveniant. Unde fit ut punctum f possit habere triplicem propensionem, cùm sint tria puncta per quae possit descendere; puncta autem m, n, o unicam tantùm, cùm sint tantùm una puncta per quae possint moveri. Duximus autem lineas fg, fB, mi etc. non quòd velimus ita lineam mathematicam aquae descendere, sed ad faciliorem demonstrationis intelligentiam. Cùm enim nova sint, et mea quae dico, multa necessariò supponenda sunt, non nisi integro tractatu explicanda, satis igitur me demonstrasse existimo quod susceperam.

⁺Ex objecto autem argumento sequitur, si reverâ descendat aqua ex utroque vase, fundis illorum eodem momento sublatis, in nullâ parte motûs imaginabili tantum gravitare aquam vasis B quantum aqua vasis D-tum propter deter-

+ novembre ou décembre 1618

a) ea premi omis.

b) illum.

c) le ms porte: agitanter.

1) Cf. la note de la page 53.

+ c est ratio ae tuum motum rpetuum firmat^d)2).

d) cette note marginale est écrite de la même main, que le texte; donc copiée sur l'original. Le relieur du manuscrit a coupé les caractères entre crochets.

2) Cf. t. I, pp. 39-40,

[p. 55]

⁺minatam celeritatem cujuslibet corporis, unde fit ut ibi dici possit infimas aquae partes in vase B attrahere superiores quodammodo efficereque ut celeriùs descendant motu vacui quàm fert illorum motus naturalis, tum etiam quia, si supponamus ordinatè et mathematicè totam aquam simul utriusque vasis descendere, longitudo linearum mi, nD, ol semper eadem remanebit, linearum autem fg, fB, fh perpetuò minuetur nullumque instans in motu potest imaginari, in quo hae lineae illis non sint breviores.

Ex dictis clarè sequitur quantò plus aqua in fundo vasis B gravitet quàm in fundo vasis A, tantò scilicet quantò linea fB longior est quàm PA^a). Sequitur secundò aquam in fundo vasis C aeque gravitare atque in fundo vasium B et D, ex praemissâ demonstratione.

Jam verò consideremus non solum aquae gravitationem^b) in fundo vasium, sed vasorum ipsorum simul cum aquâ illis injectâ gravitationem. Quam aequalem esse vasis C et vasis D, dum stant in aequilibrio et quiescunt, sic probo:

Omnia quae adigere possunt ut descendant, in utroque sunt aequalia; ergo <etc.> Probo antecedens^c): primò enim vasa sunt posita ejusdem ponderis; aqua autem aequaliter premit fundum unius atque alterius et in utroque tali modo ut si totum vas descenderet, aquae gravitatio totum suum finem consequeretur; ergo etc.

Hoc posterius probo: si enim descenderet, verbi gratiâ, vas per unum minimum imaginabile, aqua ex q descenderet versus partem s, et iterum versus C, ut impleret locum relictum a corpore fixo E^d), sicque^e) moveretur per celeritatem 1½. Item aqua in r per celeritatem etiam 1½. Quod aequipolleret celeritati trium punctorum m, n, o in vase altero, quorum unumquodque descendit per celeritatem 1.

Denique totum vas B non tantum gravitat quàm vas C, etiamsi aqua fundum utriusque aequaliter premat. Si enim imaginetur vas B descendere, suum finem planè aqua non consequetur, ut faciet in vase C. Tunc enim descendet tantum aqua in loco f per celeritatem unius, quae tamen premit fundum ut tria, atque eadem est eorum duorum differentia qualis est illius qui, in navi existens, baculo sive conto nautico alteram ejusdem navis partem propelleret, et illius qui conto littus ipsum vel corpus aliquod aliud à navi separatum pulsaret: hic enim navim moveret, alter nullo modo. Quod tam perspicuum est ut erubescam me nudius tertius¹⁾ illud non advertisse. Haec quae jam scripsi, non solum ut tibi aliquod monimentum mei relinquerem^f), sed etiam dolore et iracundiâ motus, quod nuper rem adeò facilem ex tempore non potuerim explicare, nec quidem concipere.

+ novembre ou décembre 1618

a) le ms porte seulement A.

b) gravitatione.

c) Ergo probo antecedens.

d) e.

e) sicquid.

1) Cf. les notes ci-dessus pp. 53 et 54.

f) reliquerem.

d) cette note marginale est écrite de la même main, que le texte; donc copiée sur l'original. Le relieur du manuscrit a coupé les caractères entre crochets.

2) Cf. t. I, pp. 39-40,