De Zeventiende Eeuw. Jaargang 12
(1996)– [tijdschrift] Zeventiende Eeuw, De–
[pagina 253]
| |
Huygens et les Bernoulli
| |
[pagina 254]
| |
il étudie la caténaire non uniformément chargée et la caténaire extensible pour poser finalement le problème de l'elastica et donner son logogryphe de la solution. Il termine par une remarque sur l'identité de la caténaire et de la voilière qui préoccupera beaucoup Huygens.Ga naar eind12. En 1692, les frères Bernoulli comme Huygens, commencent à travailler sur les caustiques et sur le problème de de Beaune. Les limites de cet article ne nous permettent pas d'analyser l'ensemble des problèmes qui furent traités conjointement par les trois savants. Nous nous concentrerons sur deux évènements: La querelle de Huygens avec Catelan à propos du centre d'oscillation et l'étude par Huygens du problème de la caténaire posé par Jacob Bernoulli. Ces deux études nous permettrons de mieux cerner l'élaboration par Huygens des notions d'énergie cinétique et potentielle ainsi que de travail. La première étape mène Huygens à la loi conservation de l'énergie alors que la deuxième lui fait faire les premiers pas sur le chemin du principe des travaux virtuels qui sera finalement énoncé par Johann Bernoulli. | |
I. La querelle avec Catelan et la conservation de l'énergieEn 1681, l'abbé CatelanGa naar eind13. attaque brutalement la proposition IV de la dernière partie de l'HorologiumGa naar eind14. qui concerne la détermination du centre d'oscillation. Huygens entame sa réponse à Catelan en s'étonnant: j'ay été surpris de voir qu'on ait attaqué ma Théorie du centre de Balancement, où personne depuis neuf ans qu'elle est imprimée n'avoit trouvé rien à redireGa naar eind15. Pour comprendre l'enjeu, reportonsnous à un manuscrit sur le centre d'oscillation écrit par Huygens vingt ans plus tôt:‘Méthode pour trouver des pendules simples isochrones avec des pendules composés linéaires donnés. 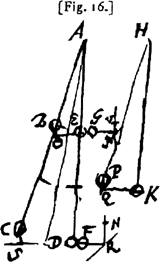
Fig. 1
| |
[pagina 255]
| |
Il s'agit de montrer qu'un pendule physique, simplement composé, dans le cas évoqué par Huygens, de deux masses B et C alignées sur un fil, est isochrone au pendule mathématique de masse égale à la totalité de la masse du pendule physique et concentrée au centre de gravité K de ce dernier. Pour donner prise au calcul et établir une équation, Huygens imagine le stratagème qui suit: ‘Pour trouver une base de ce calcul, supposons que les globes B et C, après avoir exécuté les demi-oscillations BE et CD rencontrent les globes égaux G et F. Or nous prenons ceux-ci, de même que B et C, parfaitement durs; B et C transmettront donc tout leur mouvement aux globes G et F, et le pendule linéaire AED demeurera immobile.’Ga naar eind16. Les globes B et C du pendule physique descendent l'un d'une hauteur BO et l'autre d'une hauteur CS. Ils ont donc chacun acquis une énergie cinétique déterminée par l'égalité entre l'énergie potentielle et l'énergie cinétique. Aujourd'hui, nous écririons: ½mv2=mgh où v est soit la vitesse de B soit celle de C et h est soit BO soit CS. Ces deux billes heurtent alors deux billes au repos G et F qui leur sont identiques. Il s'agit d'un cas particulier des lois de choc de deux billes animées de vitesses différentes que Huygens connait depuis 1656. Il écrit dans le De motu corporum ex percussione: ‘PROPOSITION VIII.Pour montrer cela Huygens part de l'expérience suivante: ‘... Supposons que le corps A ait acquis sa première vitesse AC, avec laquelle il se mouvait vers le contact, en tombant de la hauteur HA, de telle manière qu'après être descendu jusqu'en A il ait changé son mouvement vertical en un mouvement horizontal de la vitesse AC; et que pareillement le corps B ait acquis la vitesse BC en tombant de la hauteur KB;Ga naar eind17. 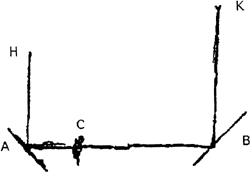
Fig. 2Ga naar eind18.
| |
[pagina 256]
| |
Cette figure tirée d'un autre manuscrit et donnée en note par les éditeurs des Oeuvres de Huygens, montre clairement comment Huygens visualisait la transformation de l'énergie potentielle en énergie cinétique. La bille tombe d'une certaine hauteur sur un plan incliné de 45o sur lequel son mouvement est dévié en un mouvement horizontal dont le carré de la vitesse est lié à cette hauteur:
‘ces hauteurs sont donc dans la raison doublée des vitesses, c'est-à-dire: comme le carré AC est au carré CB, ainsi HA à KB. Mais si ensuite, après le choc, les corps A et B changent leurs mouvements horizontaux, dont les vitesses sont mesurées par CD et CE, en des mouvements perpendiculaires vers le haut: on sait que le corps A arrivera à la hauteur AL’.Ga naar eind19. 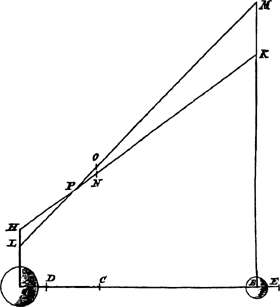
Fig. 3
Huygens va imaginer, comme sur la figure supra, cette hauteur et son homologue pour l'autre bille, différentes de celles d'où les billes sont parties. Il montre ensuite qu'une telle supposition entraîne que le centre de gravité des deux billes ne remonte pas à la hauteur d'où il est parti. Ce qui est impossible. En résumé le raisonnement de Huygens est le suivant: Deux billes sont lâchées chacune d'une certaine hauteur. Leur centre de gravité part donc d'une certaine hauteur. Chacune de ces billes acquiert une certaine énergie cinétique et donc une certaine vitesse dans sa chute. Les billes entrent en collision et ressortent de cette collision avec des vitesses telles qu'elles remontent en convertissant à nou veau leur énergie cinétique en énergie potentielle, elles remontent à une hauteur telle que leur centre commun de gravité remonte exactement à la hauteur d'où il est parti. ‘Or,’ affirme-t-il, ‘en mécanique c'est un axiome très certain que par un mouvement des corps qui résulte de leur gravité le centre commun de leur gravité ne peut pas s'élever.’Ga naar eind20. Ce qui avait été établi par Torricelli en 1644: ‘Nous poserons en principe que deux graves, liés ensemble, ne peuvent se mouvoir d'eux mêmes, à moins que leur commun centre | |
[pagina 257]
| |
de gravité ne descende.’Ga naar eind21. Il en résulte pour Huygens que la collision conserve l'énergie cinétique des billes, ce qui détermine leurs vitesses après la collision. Dans le texte de 1661, ce même type de raisonnement permet à Huygens d'établir la relation qui détermine le point où il faut placer la masse concentrée pour que le pendule mathématique ainsi formé oscille avec la même vitesse que le pendule physique composé de deux masses. 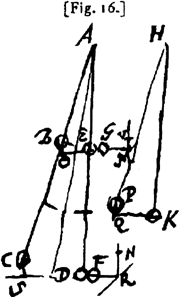
Fig. 4
‘Par conséquent lorsque les globes G et F retournent avec des vitesses égales à celles qu'ils avaient reçues et frappent E et D, ceux-ci recouvreront de leur part tout leur mouvement et remonteront d'après nos lois du mouvement les arcs EB et CD de la même manière qu'ils les avaient parcourus en sens inverse, ramenant évidemment en même temps la barre AD en AC. Il en résulte que le centre de gravité composée des globes G et F, après qu'ils ont reçu de la part de E et de D leur mouvement et qu'ils se sont élevés par ce mouvement aussi haut que possible, atteint une hauteur égale à celle du centre de gravité des globes B et C. ... Ceci est evident d'apres la mecanique.’Ga naar eind22. 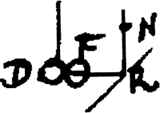
Fig. 5
La figure 5, extraite de la figure 4 montre d'ailleurs le même processus expérimental que la figure 2. Il est bon pour la suite de notre exposé d'ajouter ici que mgh | |
[pagina 258]
| |
représente non seulement l'énergie potentielle de la bille placée à une certaine hauteur mais aussi le travail qu'il faut effectuer pour amener cette bille à la hauteur h. L'équation de conservation de l'énergie n'apparaît pas dans le texte que Huygens soumet à la Royal SocietyGa naar eind23. en 1669. Elle apparaît par contre dans le texte qu'il donne, trois mois plus tard, au journal des savantsGa naar eind24. ainsi que dans son texte De motu corporum ex percussioneGa naar eind25. dont la première version date de 1656 mais dont la version plus élaborée est postérieure à l'Horologium. Dans le Journal des savants, cette règle porte le no6: ‘La somme des produits faits de la grandeur de chaque corps dur, multiplié par le quarré de sa vitesse, est toujours la mesme devant et apres leur rencontre.’Ga naar eind26. Elle correspond à la proposition XI du De motu: ‘Dans le cas de deux corps qui se rencontrent, ce que l'on obtient en prenant la somme de leurs grandeurs multipliées par les carrés de leurs vitesses sera trouvé égal avant et après la rencontre: savoir lorsque les rapports des grandeurs et des vitesses sont données en nombres ou en lignes.’Ga naar eind27. Dans la proposition IV de la quatrième partie de l'Horologium oscillatorium on trouve un énoncé quelque peu différent de l'axiome sur les centres de gravité: ‘Si un pendule composé de plusieurs poids et commençant son mouvement considéré à partir du repos, a exécuté une partie quelconque de son oscillation entière et qu'on se figure qu'à partir de ce moment, le lien commun étant rompu, chacun de ces poids tourne sa vitesse acquise vers le haut et s'élève à la plus grande hauteur possible, par ce fait le centre commun de gravité remontera à la hauteur qu'il avait avant le commencement de l'oscillation.’Ga naar eind28. Cette proposition IV vient compléter l'hypothèse fondamentale ‘Hypothèse I. Nous supposons que lorsqu'un nombre quelconque de poids commencent à se mouvoir par leur propre gravité, le centre commun de gravité ne peut s'élever à une hauteur supérieure à celle où il se trouvait au début du mouvement. ... Or pour que notre hypothèse ne fasse scrupule à personne, nous montrerons qu'elle ne signifie que ce que nul n'a jamais nié, savoir que les corps graves ne montent pas d'eux mêmes.’Ga naar eind29.L'Abbé Catelan veut prouver l'erreur d'Huygens en faisant appel à l'expérience suivante: 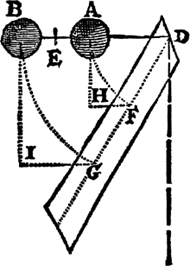
Fig. 6
| |
[pagina 259]
| |
Deux masses ponctuelles, formant deux pendules de longueurs différentes, sont lâchées de l'horizontale DAB. Arrivé aux plan DGF, chaque pendule aura acquis une vitesse dont le carré est proportionnel à la hauteur qu'il a franchie, AH ou BI. Si l'on considère à présent un pendule composé des deux mêmes masses liées entre elles et qui descend depuis l'horizontale DB jusqu'au plan incliné DFG: ‘Le pendule qu'ils composeront acquierra autant de vitesse que la somme des deux pendules simples, puisque le centre de pesanteurs commun E demeurera le mesme qu'il estoit. Il imagine ensuite que le pendule composé heurte le plan incliné DFG et que les massses se détachent l'une de l'autre et remontent à une hauteur qui doit être proportionnelle au carré des vitesses qu'ils ont acquises en tombant, c'est-à-dire des vitesses proportionnelles aux carrés des rayons DF et DG. Les masses vont donc remonter à des hauteurs différentes de celles dont elles sont descendues. Huygens répond en 1682. Il reprend l'exemple de Catelan et dit que les billes remontent bien à des hauteurs différentes mais que ‘le centre de pesanteur commun des poids A, B montez en L, M sera à même hauteur qu'il estoit en E devant que le balancement fut commencé.’Ga naar eind31. 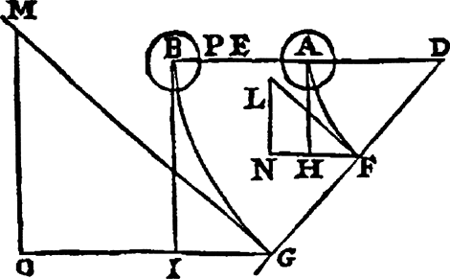
Fig. 7
Catelan contre-attaque, répète son idée et ramène la question à une proposition d'algèbre. C'est alors que Jacob Bernoulli intervient pour statuer sur le controverse: ‘Tout le discours de Mr Catelan ne tend qu'à prouver que la somme des racines de deux grandeurs quelconques ne peut être coupée en deux parties, en sorte qu'elles soient proportionnelles aux grandeurs données, & que la somme de leurs quarrés soit égale à celle de ces mêmes grandeurs: ce qui ne lui est pas contesté par Mr. Hugens qui soutient seulement que la somme de deux autres qui ne sont que pro- | |
[pagina 260]
| |
portionnelles aux quarrés des dites parties; ce qui est aussi vrai.’Ga naar eind32. Il donne, sans entrer dans la physique du problème, un exemple de valeurs qui satisfont au problème tel que vu par Huygens. Indépendamment, Huygens donne le même exemple numérique dans sa réponse du 8 juin 1684. Nous savons qu'il n'avait pas lu le texte de Bernoulli car Cl. Perrault lui annonce le 8 juillet: ‘qu'un mathématicien nomme Barnoully a pris vostre défence contre l'Abé Catelan’Ga naar eind33. et le 10 Août, il annonce à son père: ‘L'on m'a envoyé le Journal des Sçavants, ou j'avois fait mettre ma réponse a l'Abbé Catelan et l'on adjoute qu'un certain Bernouilli, de qui j'ay veu un traité des Comètes en Latin a entrepris ma querelle contre luy, ce qui sera fort bien.’Ga naar eind34. Suit une réponse,Ga naar eind35. de Catelan à Bernoulli, qui ne suscitera pas beaucoup de réaction. Il faudra attendre deux ans avant que Jacob reprenne la plume à ce sujet. Il contredit le postulat fondamental de Catelan mais marque une hésitation relative au postulat énergétique fondamental de Huygens: ‘Avant de finir, je dirai en faveur de Dn. Catelan que même si comme il le prétend, le centre de gravité remonte plus haut qu'il n'est descendu, il n'en découle pas obligatoirement la possibilité d'un mouvement perpétuel comme le prétend Huygens.’Ga naar eind36. Rappelons-nous en effet l'affirmation de la quatrième partie de l'Horologium: ‘Or, l'hypothèse que nous avons faite s'applique aussi aux corps liquides. Par elle non seulement tout ce qu'Archimède a des corps flottants peut-être démontré, mais aussi beaucoup d'autres théorèmes de mécanique. Et véritablement, si les inventeurs de nouvelles machines qui s'efforcent vainement d'obtenir le mouvement perpétuel, savaient faire usage de cette hypothèse, ils découvriraient aisément eux-mêmes leurs erreurs et comprendraient que ce mouvement ne peut aucunement être obtenu par des moyens mécaniques.Ga naar eind37. Affirmation qui servait de fondement à la réplique de Huygens à l'Abbé Catelan de 1684: ‘Donc,’ en utilisant le principe de Catelan, ‘ce centre de gravité montera plus haut que d'où il étoit descendu... ce qui est contre le grand principe des mécaniques; & si Mr. l'Abbé peut faire en sorte qu'il soit vray, il aura trouvé le mouvement perpétuel.’Ga naar eind38. Ajoutons encore que Jacob était sensibilisé à ce problème. Il écrit dans ses Positionum Philosophicarum: Op. VII, Thèse 75: Sur la Roue bâloise construite par Jeremia Mitzio et qui n'a pas eu le succès escompté, ‘mais ne rend pas mince l'espoir de trouver un mouvement perpétuel purement artificiel.’Ga naar eind39. 1685 a vu la parution de deux articles de PapinGa naar eind40. sur le mouvement perpétuel qui seront aussi commentés par Jacob en 1686. Il y consacre trois textesGa naar eind41. et, en 1690, dans son tout premier travail, De effervescentia et Fermentatione,Ga naar eind42. le jeune Johann Bernoulli consacre un appendice au mouvement perpétuel. Il place un tube capillaire dans un récipient rempli d'eau et pense que l'eau montera dans le tube, puis débordera de ce dernier et retournera dans le vase, et ainsi éternellement. Pourtant, plus tard, Johann se range aux côtés de Huygens. Il écrit à son frère, Jacob Bernoulli, le 17 juin 1691: ‘Quant à nos affaires Mathématiques, je suis bien fache de ce que Vous n'avez pas differe encore pour quelque temps Vos inventions touchant le centre d'oscillations, car i'ay trouve avant avoir reçûe Votre lettre une belle methode pour chercher ce centre qui ce me semble est plus generale que la Votre laquelle ne peut pas s'accommoder ni pour | |
[pagina 261]
| |
Revenons au texte de Jacob de 1686 sur le centre d'oscillation.Ga naar eind44. Comme il n'admet pas le principe énergétique de Huygens, il tente de résoudre différemment, au moyen du levier, le paradoxe posé par Catelan. Il n'y arrivera pas complètement dans ce texte et il faudra attendre que de l'HopitalGa naar eind45. montre, en 1690, la possibilité d'accorder la démonstration énergétique de Huygens et celle effectuée au moyen de la loi du levier par Jacob. Il suffit pour cela de remplacer la vitesse à laquelle il fait appel par ‘la vitesse commençante’ c'est-à-dire une grandeur proche de notre accélération. Jacob poursuivra cette recherche jusqu'à la fin de sa vie et publiera encore en 1703, trois travauxGa naar eind46. à ce sujet. Mais ceci est une autre histoire.Ga naar eind47. | |
II. La caténaire et le principe des travaux virtuelsEn 1690, précisément à l'époque où l'Hopital publie son articleGa naar eind48. sur le centre d'oscillation, Jacob BernoulliGa naar eind49. comme HuygensGa naar eind50. poursuit la réflexion sur l'isochrone entamée par LeibnizGa naar eind51. en 1687. Dans un appendice à sa réponse, Jacob pose la question de la caténaire ou funiculaire: Trouver la courbe adoptée par un fil lâche et suspendu librement entre deux points.Ga naar eind52. | |
[pagina 262]
| |
Ce problème n'est pas neuf pour Huygens puisque c'est le premier qu'il ait affronté, à 17 ans, en 1646, suivant une suggestion de Mersenne. A cette occasion, il avait commencé un petit traité axiomatique de la caténaire fondé, d'abord, sur quatre axiomes puis sur cinq dans une deuxième rédaction. La deuxième version, outre l'adjonction d'un axiome, modifie le deuxième axiome. Huygens en fait une particularisation à la statique de l'axiome de Torricelli déjà évoqué. 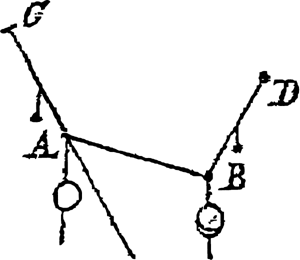
Fig. 9
Première version de l'axiome 2: ‘secondement que deux ou plusieurs gravitez A et B attachez à la corde CABD qui est tenue en C et D, ne peuvent demeurer en repos que d'une seule façon.’Ga naar eind53. 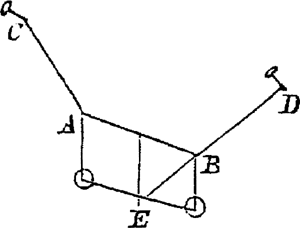
Fig. 10
| |
[pagina 263]
| |
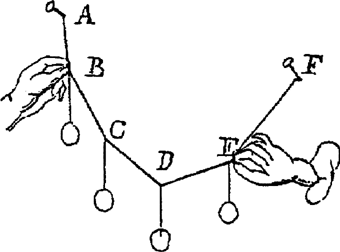
Fig. 11
Dans la seconde version de cet axiome, il ajoute: ‘et de manière à ce que leur centre de gravité, qui ici est E, descende le plus possible et s'approche du plan de la terre.’Ga naar eind54. De cette manière apparaît chez Huygens l'ébauche de l'Hypothèse fondamentale de la quatrième partie de l'HorologiumGa naar eind55. déjà évoquée. Cette ébauche ne s'applique qu'à la statique mais nous avons déjà rencontré sa généralisation à la dynamique dans les problèmes de choc. Cette généralisation figure également dans l'Horologium. Dans les manuscrits de la même année, Huygens applique cet axiome à la construction de la caténaire: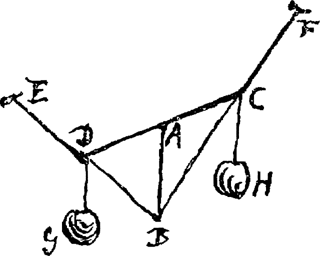
Fig. 12
| |
[pagina 264]
| |
Dans le cas de deux poids attachés à un fil maintenu par deux clous, le fil se placera de manière à ce que le point de concours B des prolongements des fils ED et FC soit à l'aplomb du centre de gravité des deux masses, sans quoi leur centre de gravité A pourrait être rapproché du centre de la Terre. Ce raisonnement lui permet de déterminer, de proche en proche les points de la caténaire. 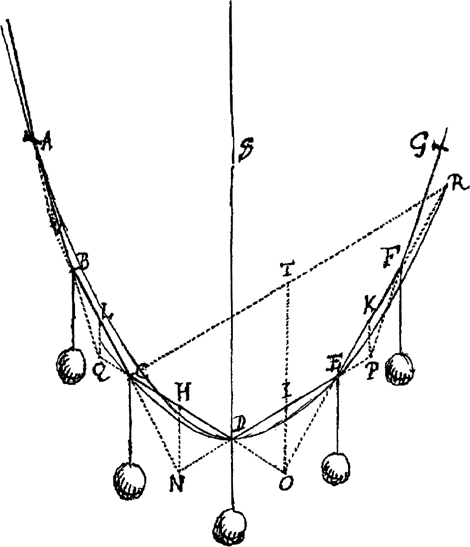
Fig. 13
De nombreuses années plus tard, en 1688, Huygens reviendra sur le problème de deux masses attachées à une corde qui ouvre la voie à l'étude de la caténaire. Pour comprendre la solution qu'il proposera alors à ce problème, il faut d'abord retracer le cheminement de son raisonnement à travers des problèmes très différents. Dans le premier cas, en 1659, il s'agit de déterminer le poids d'un corps sur un plan incliné. Il estime que les poids sont dans le même rapport que les hauteurs [verticales] qui seraient franchies par ces deux corps si on les écartait de l'équilibre. Il sait que | |
[pagina 265]
| |
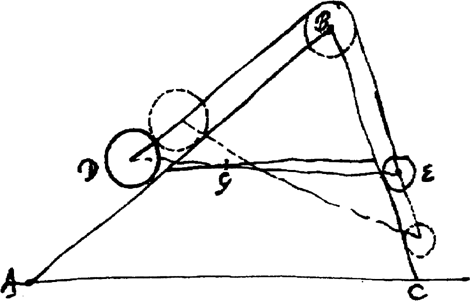
Fig. 14
la corde garde la même longueur, donc la longueur franchie le long des deux plans inclinés est la même. Il obtient une relation entre les hauteurs verticales franchies par les poids et ces poids: Cette relation est équivalente à celle que nous donnerions aujourd'hui en nommant αE et αD, les deux angles aux pieds des plans inclinés: PEsinαE = PDsinαD. Huygens justifie son équation: ‘parce que leur centre de gravité commun G ne descend pas même si les poids commencent à se mouvoir mais qu'il reste à la même hauteur.’Ga naar eind56. Nous nous retrouvons dans le même contexte que dans le cas de son étude des chocs. De notre point de vue actuel il y a une différence. Dans le cas des chocs la hauteur est caractéristique de l'énergie potentielle de la bille qui se transforme en énergie cinétique. Ici le travail à effectuer pour amener l'une des billes à une certaine hauteur est compensé par le travail fourni par la descente de l'autre bille. Mais dans les deux cas l'expression de la quantité est mgh. Cette notion de travail est bien connue d'Huygens car elle est à la base du travail ‘Explication des engins par l'ayde desquels on peut avec une petite force lever un fardeau fort pesant!’, que Descartes transmet, en 1637, à Constantijn Huygens. On y trouve le principe suivant: ‘qu'il ne faut ni plus ni moins de force, pour lever un corps pesant à une certaine hauteur, que pour en lever un autre moins pesant à une hauteur d'autant plus grande qu'il est moins pesant, ou pour en lever un plus pesant à une hauteur d'autant moindre.’Ga naar eind57. La force dont parle Descartes correspond à ce que nous appelons le travail à effectuer.
Dans un autre manuscrit datant du 14 mars 1659, Huygens traite un problème tout | |
[pagina 266]
| |
différent en imaginant une fois de plus un déplacement pour déterminer un équilibre:
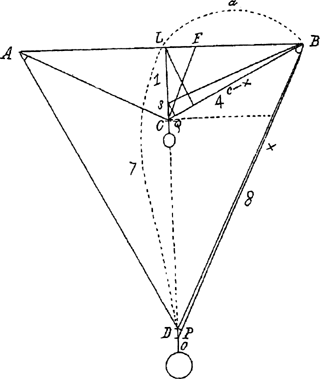
Fig. 15
‘Soient A et B des poulies, AC = DA, AC = CB, AD = DB, on donne les poids suspendus en C et D, on donne aussi AB et la longueur du fil ACBDA. Il faut trouver dans quelle situation les poids ainsi suspendus sont au repos. Considérons un point S de CL et joignons SB. Celle-ci est à considérer comme presque parallèle à BC parceque CS est un minimum. Soit SQ perpendiculaire à BC. Si donc C montait en S, BS serait plus court que BC d'une quantité QC. En même temps D descend aussi en O; distance DO que l'on trouve de la manière suivante:’Ga naar eind58. Nous pouvons aisément suivre le raisonnement de Huygens fondé sur le principe de Torricelli. Il considère une autre configuration quelconque du système et détermine l'équilibre en minimisant la position du centre de gravité. Il est clair que le principe des travaux virtuels n'est pas encore complètement élaboré mais que Huygens fait un pas dans la précision de ce principe en demandant que le déplacement soit infinitésimal. En 1667, nous voyons apparaître l'équation que ce raisonnement qui lui permet d'écrire dans le cas de la recherche de l'équilibre d'un système de cordes nouées en un point et supportant des poids. Quelques années plus tard encore, en 1688, Huygens applique son raisonnement d'abord à une barre TQ coincée entre deux droites AQ et AE. Soulignons en la phrase caractéristique: ‘Adaptons une droite CE égale à TQ dans une autre position.’Ga naar eind59. | |
[pagina 267]
| |
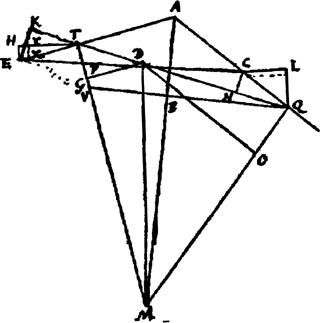
Fig. 16
Il compare une fois de plus l'ascension d'une extrémité à la descente de l'autre et en tire les conséquence sur la position du centre de gravité. Le même raisonnement s'applique à l'étude de l'équilibre de deux poids attachés à un fil. 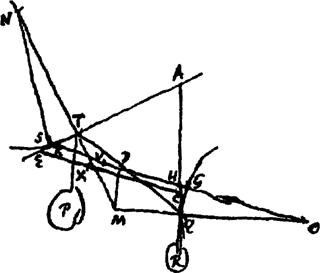
Fig. 17
| |
[pagina 268]
| |
Huygens déplace légèrement le fil maintenant les poids: NT est déplacé en NS et OQ en OG. Il montre alors comme dans les autres démonstrations que: ‘De cette manière le centre de gravité des poids P, R monterait ce qui est impossible.’Ga naar eind60. Cette phrase rituelle ponctue chacune de ses démonstrations. Avec ces derniers problèmes, nous nous rapprochons du problème de la caténaire et nous ne nous étonnons pas de voir Huygens faire appel à ce procédé pour s'attaquer au problème posé par Jacob Bernoulli en 1690. Nous trouvons dans les explications qu'il consigne dans ses manuscrits à propos du chiffre qu'il a publié pour masquer sa solution un texte intitulé: ‘Fondement de tout ce que nous avons découvert à propos de la courbe caténaire’Ga naar eind61. où l'on retrouve la première construction de 1646. 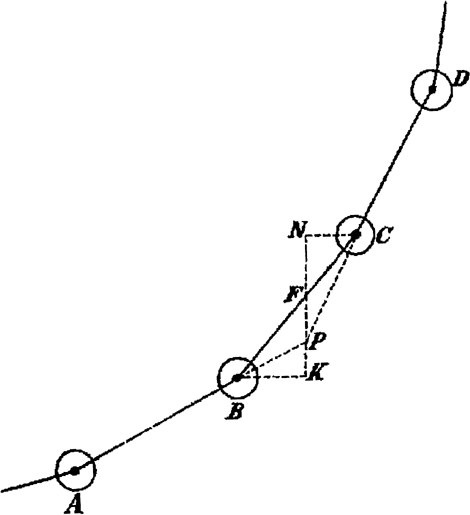
Fig. 18
Sa solutionGa naar eind62. est publiée de manière très succincte comme celles de Johann BernoulliGa naar eind63. et de Leibniz.Ga naar eind64. Nous pouvons nous faire une meilleure idée de celle de Johann à travers ses leçons à de l'Hopital où il donne, comme Huygens dans le manuscrit que nous venons de citer, les détails du calcul qui fonde son article. Sa méthode est très différente de celle de Huygens et fait appel au Calcul leibnizien. | |
[pagina 269]
| |
Néanmoins, la dernière propriété aurait fait plaisir à Huygens: ‘Si l'on se représente une infinité de courbes tracées sur EF, égales à la funiculaire EBF, que l'on étend en une droite, et que l'on met en ordonnée en chacun des points de chaque [courbe] étendue des droites égales à leurs distances respectives de la ligne EF, parmi toutes les aires qui sont ainsi formées, celle qui est engendrée par la funiculaire sera la plus grande. Ce que l'on montre au moyen de cet axiome que le centre de gravité occupe l'emplacement le plus bas possible.’Ga naar eind65. Mais alors qu'Huygens considérait le centre de gravité de la courbe, Johann parle ici du centre de gravité de l'aire comprise entre la courbe et l'horizontale passant par les points de fixation de la chaîne. 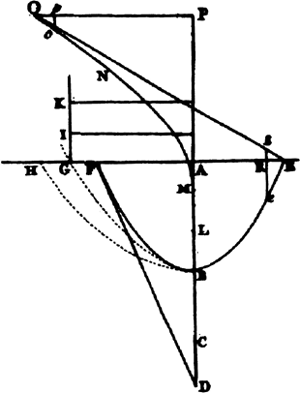
Fig. 19
Pour ce qui concerne Jacob,Ga naar eind66. nous ne trouvons pas chez lui ce type de raisonnement à propos de la chaînette et les réticences qu'il a montrées vis-à-vis du principe énergétique de Huygens font que nous ne devons pas nous en étonner. Cependant lorsqu'il propose et tente de résoudre le problème de l'élastica,Ga naar eind67. et dans le même esprit celui des isopérimètres,Ga naar eind68. il commence par considérer les propriétés de position minimale du centre de gravité. Mais il s'agit là aussi d'une autre histoire. | |
III. ConclusionEn conclusion, je poserai une question. Dans quelle mesure la méthode des travaux virtuels telle qu'appliquée par Huygens à des cas de statique a-t-elle transpiré à travers la correspondance du Marquis de l'Hopital ou de Leibniz et dans quelle mesure a-t-elle pu influencer la rédaction de la lettre de Johann Bernoulli à Varignon, datée du 26 janvier 1717 et publiée par Varignon dans la Nouvelle Mécani- | |
[pagina 270]
| |
que? Johann Bernoulli y écrit: ‘Concevez plusieurs forces différentes qui agissent suivant différentes tendances ou directions pour tenir en équilibre un point, une ligne, une surface, ou un corps; concevez aussi que l'on imprime a tout le systeme de ces forces un petit mouvement, soit parallèle a soi-même suivant une direction quelconque, soit autour d'un point fixe quelconque: il vous sera aise de comprendre que par ce mouvement chacune de ces forces avancera ou reculera dans sa direction, a moins que quelqu'une ou plusieurs des forces n'ayent leurs tendances perpendiculaires a la direction du petit mouvement; auquel cas cette force, ou ces forces, n'avanceroient ni ne reculeroient de rien; car ces avancemens ou reculemens, qui sont ce que j'appelle vitesses virtuelles, ne sont autre chose que ce dont chaque ligne de tendance augmente ou diminue par le petit mouvement; et ces augmentations ou diminutions se trouvent, si l'on tire une perpendiculaire a l'extremite de la ligne de tendance de quelque force, laquelle perpendiculaire retranchera de la meme ligne de tendance, mise dans la situation voisine par le petit mouvement, une petite partie qui sera la mesure de la vitesse virtuelle de cette force.’Ga naar eind69. |
|