De Zeventiende Eeuw. Jaargang 10

[p. 93]

Stevin en Maurits
H.H. Kubbinga

‘Het gaet hier mede ghelijck met onse schaduwe welcke haer navolgende lichamen ontvliet ende haer ontvliedende navolght.’
S. Stevin.^1.

1. Vita politica. Het burgherlick leven, Leiden, F. van Ravelenghien, 1590, p. 26.

1. Inleiding

De biografische gegevens omtrent Simon Stevin (1548-1620) zijn door de wetenschapshistoricus E.J. Dijksterhuis (1892-1965), in zijn standaardwerk^2., op hun waarheidsgehalte getoetst. Wat overbleef was gering, vooral waar het Stevins verhouding tot zijn broodheer, Maurits van Nassau (1567-1625), betreft. Onduidelijk is bijvoorbeeld of Maurits tijdens zijn kortstondige studie in Leiden (19 april 1583-10 juli 1584) zijn uit Brugge afkomstige jaargenoot persoonlijk heeft gekend.^3. Van een krijgskundige samenwerking is pas sprake vanaf 1593, waarbij Stevin fungeert als persoonlijke adviseur van de graaf. In 1603 wordt Stevin door de laatste voorgedragen voor een Staats traktement; eind januari 1604 volgt inderdaad zijn benoeming tot ‘Quartiermeester tot het afsteecken der quartieren’, d.w.z. lid van de tweehoofdige leiding van de militaire intendance, tegen een salaris van £500 per jaar.^4.

Tussen 1593 en 1605 moet Stevin hebben gefungeerd als privé-leraar en tutor van de bevelhebber der opstandige Nederlanden. In dit verband schreef Stevin talloze didactisch getinte verhandelingen, over alle onderwerpen waar Maurits belangstelling voor had. Te oordelen naar de gebundelde versie van deze teksten, de beroemde Wisconstighe ghedachtenissen^5., moet de betrokkene een universele belangstelling hebben gehad. In het nu volgende willen wij op basis van diezelfde Wisconstighe ghedachtenissen een indruk geven van de interesses van Maurits, van de wijze waarop hij bij zijn studie te werk ging en van de rol die Stevin bij een en ander heeft gespeeld. Op voorhand kan al gesteld worden dat de tutor en zijn negentien jaar jongere student aan elkaar gewaagd waren: hij die zou uitgroeien tot de grootste strateeg van het eind van de zestiende en het eerste kwartaal van de zeventiende eeuw had zich inderdaad verzekerd van de steun van één van de leidende geesten van zijn tijd. De zgn. ‘clootcrans’ waarmee Stevin in 1586 - lang vóór Galileo Galilei, al was het niet als eerste - de wet van het hellend vlak aantoonde (met een beroep op de onmogelijkheid van een perpetuum mobile), staat tegenwoordig symbool voor die combinatie van eenvoud en genie, waardoor een vondst uitgroeit tot een echte wetenschappelijke doorbraak. Zoals de ‘clootcrans’ eens de titelbladen van Stevins oeuvre sierde (zie Fig.1), zo luistert hij dezer dagen de omslag op van het meest prestigieuze wetenschapshistorische naslagwerk van dit moment, de Dictionary of scientific biography.^6. In het bijzonder Dijksterhuis heeft zich ingezet voor een evenwichtige historische waardering van Stevins bijdragen aan cultuur, techniek en wetenschap. De K.N.A.W.-commissie die zorg heeft gedragen voor de uitgave van The principal works of Simon Stevin^7. stond dan ook onder zijn voorzitterschap. Hoewel onze studie van de verhouding tussen Stevin en Maurits gebaseerd is op eigen bronnenonderzoek, zijn wij schatplichtig aan het door Dijksterhuis in zijn baanbrekende monografie geschilderde beeld.^8. Overigens is onze aanpak een andere.

2. E.J. Dijksterhuis, Simon Stevin, 's-Gravenhage, M. Nijhoff, 1943, Hoofdstuk I.

3. Dijksterhuis, op. cit. (noot 2), p. 10, noot 1.

4. Dijksterhuis, op. cit. (noot 2), p. 10-11.

5. Leiden, J. Bouwensz, 1605 en 1608 (n.b. de opgenomen verhandelingen zijn afzonderlijk gepagineerd). Het door ons geraadpleegde exemplaar was dat uit de rijke Stevin-collectie van de Provinciale Bibliotheek van Friesland (Leeuwarden; signatuur 39-Wk-folio-2). Een deel van deze collectie is afkomstig uit de toenmalige Universiteitsbibliotheek van Franeker; een ander deel stamt uit de bij legaat verkregen verzameling van J.H. Halbertsma (1789-1869). Graag danken wij de Provinciale Bibliotheek van Friesland in de persoon van conservator drs. M. Engels voor de bereidwillige medewerking.

6. Onder redactie van C.C. Gillispie, New-York, C. Scribners, 1970-1980. De aan Stevin gewijde bijdrage (deel XIII, p. 47-51) is van de hand van M.G.J. Minnaert.

7. Amsterdam, Swets en Zeitlinger, 1955-1966. Het redactie-comité bestond naast Dijksterhuis uit E. Crone, R.J. Forbes, M.G.J. Minnaert en A. Pannekoek.

8. Dijksterhuis, op. cit. (noot 2), Hoofdstuk XVII.

[p. 94]

Aan de hand van een specifiek praktisch probleem, de topzwaarheid van een belegeringsschip beladen met soldaten op trappen, willen wij laten zien waar de interesse van de Prins naar uitging en wat Stevin onderwees om daaraan tegemoet te komen. Het gaat hierbij onder andere om wiskunde, natuurkunde, zeevaartkunde, bouwkunde en krijgskunde. Wat ons betreft ligt de nadruk op de wis- en natuurkundige aspecten: wij zullen zien dat Stevin belangrijk heeft bijgedragen aan wat bekend stond als de ‘meetkunde der indivisibilia’, een op Archimedes (ca. 287-212 v. Chr.) teruggaande benadering in de wiskunde, die in de XVIIe eeuw een grote vlucht zou nemen. Het geavanceerde wis- en natuurkundeonderwijs van Stevin stond niet op zichzelf; het was, zoals wij zullen zien, een min of meer vanzelfsprekend onderdeel van zijn alomvattende kijk op cultuur, techniek en wetenschap en heeft daarom ook in breder verband een inspirerende invloed kunnen uitoefenen op bevelhebber Maurits en daarmee op het zelfbewustzijn van de jonge ‘Vereenichde Nederlanden’.

2. De Wisconstighe ghedachtenissen

De Wisconstighe ghedachtenissen verschenen in een tweedelige in-folio uitgave, in 1605 en in 1608. In het laatste jaar kwam nog een integrale Latijnse vertaling van de hand van niemand minder dan Willibrord Snellius (1580-1626)^9. op de markt en een gedeeltelijke Franse vertaling van Jan Tuning, secretaris van Frederik Hendrik.^10. Met enig recht kan worden gesproken van een massieve publiciteitscampagne ten behoeve van de stadhouder, aan de vooravond van het Twaalfjarig Bestand, een campagne die indirect gesteund werd door zijn latere opvolger en door de Leidse academie. Dat de Wisconstighe ghedachtenissen en de beide vertalingen ook feitelijk hebben bijgedragen aan Maurits' militaire faam lijkt in elk geval zeer waarschijnlijk.

De Wisconstighe ghedachtenissen bestaan uit vijf ‘stukken’, waarvan het eerste deel I van de in-folio editie uitmaakt en de laatste vier deel II. De vijf stukken zijn als volgt getiteld (tussen haakjes het jaar van verschijnen): 1. Het weereltschrift (1608); 2. De meetdaet (1605); 3. De deursichtighe (1605); 4. De weeghconst (1605); 5. Van de ghemengde stoffen (1608).

Het eerste stuk betreft wat vanouds bekend stond als ‘cosmographia’ en is opgesplitst in drie onderdelen, gewijd aan resp. goniometrie en (vlakke en sferische) trigonometrie, aardrijkskunde in ruime zin ten behoeve van het reizen te land en ter zee, en tenslotte wat tegenwoordig ‘grondmechanica’ genoemd zou worden, de bewegingen van stofmassa's (zand, klei, e.d.) aan het oppervlak van de aarde al dan niet onder invloed van waterstromen, het geheel, de aarde dus, ‘blijvende t'samen een clootsche form’. Het tweede stuk betreft vlakke en ruimtelijke meetkunde; stuk III gaat over perspectiefleer^11. en lichtweerkaatsing op vlakke en gebogen spiegels (een aangekondigd onderdeel over lichtbreking ontbreekt helaas).^12. Stuk IV handelt over de wetenschap van het wegen (in lucht en in water), meer in het bijzonder over de bepaling van het ‘swaerheyts middelpunt’ ( = zwaartepunt). In een ‘byvough’ bespreekt Stevin dan een aantal in samenwerking met Maurits uitgewerkte toepassingen: de verdeling van de draaglast over verschillende touwen en katrollen, over de problemen rond de ‘topswaerheyt’ van schepen en over de werking van

9. Hypomnemata mathematica [..], Leiden, J. Patius [=J. Paedts Iacobsz], 1608.

10. Memoires mathematiques [..], Leiden, J. Paedts Iacobsz [=J. Patius], 1608.

11. Voor een studie van Stevins perspectiefleer, zie: K. Andersen, ‘Stevin's theory of perspective: the origin of a Dutch academic approach to perspective’. In: Tractrix 2 25-62 (1990).

12. Eind september-begin oktober 1608 diende Hans Lipperhey, een brillenmaker uit Middelburg, bij de Staten-Generaal een patentaanvraag in voor ‘seecker instrument om verre te sien’, een verrekijker die ook geschikt bleek als sterrenkijker. Het instrument werd in Den Haag gedemonstreerd aan Maurits en de verschillende delegaties die daar bijeen waren voor de bestandsonderhandelingen. Het sensationele nieuws verbreidde zich snel over Europa. Galilei was in juni 1609 op de hoogte, bouwde een eigen exemplaar dat hij verder perfectioneerde. In januari 1610 deed hij de ontdekkingen (bergen op de maan; vier satellieten rond Jupiter) die de sterrenkunde op haar kop zetten. Zie: A. van Helden, ‘The invention of the telescope’. In: Transactions of the American Philosophical Society 67 (4) 1-66 (1977). In deze contekst is het ontbreken van de verhandeling over lichtbreking des te betreurenswaardiger, daar Stevin net als Galilei een vroege aanhanger was van het Copernicaanse, heliocentrische wereldbeeld. Dit blijkt uit de stof waarmee hij Maurits vertrouwd maakte met de grondslagen van de sterrenkunde. Zie: Stevin, Van den hemelloop, in op. cit. (noot 5), deel I (1608).

[p. 95]

Figuur 1. Titelpagina van de Wisconstighe G[h]edachtenissen (Provinciale Bibliotheek van Friesland, Leeuwarden; signatuur 39-WK-folio-2). De ontbrekende ‘h’ kan worden opgevat als een drukfout; elders gebruikte Stevin hem consequent.

het bit van een paardetoom. Het laatste stuk behandelt eerst enkele ‘telconstighe anteyckeninghen’ en daarna financiële bedrijfsvoering in het algemeen en die van de overheid in het bijzonder, waarbij wordt gepleit voor de zgn. Italiaanse aanpak, de bekende ‘dubbele boekhouding’ in termen van debiteuren en crediteuren.

Alles welbeschouwd kreeg Maurits van zijn tutor een gedegen cursus algemene ontwikkeling, naar tegenwoordige maatstaven variërend van voorbereidend wetenschappelijk tot uitgesproken academisch niveau, met een voorkeur voor de wiskundige en technisch interessante aspecten en toegespitst op de situatie in de ‘Vereenichde Nederlanden’. Een ‘ingenieursopleiding te velde’, zou men kunnen zeggen. Uit de ‘voorreden’ van de Wisconstighe ghedachtenissen blijkt inderdaad dat de bevelhebber het door Stevin in manuscriptvorm voorbewerkte materiaal op doortocht met zijn leger en tijdens het beleg van diverse steden bestudeerde, in de vrije tijd die het krijgsbedrijf hem overliet. Vaak ook wisselde hij mondeling van gedachten met zijn leermeester, met wie hij ten slotte dagelijks verkeerde, aangezien Stevin als ‘ingenieur’^13. deel uitmaakte van zijn generale staf. Dat de lessen uiteindelijk in druk verschenen had drie redenen, zo voert Stevin aan in de genoemde ‘voor-

13. In zijn recente proefschrift Nederlandse ingenieurs en de fortificatiewerken in het eerste tijdperk van de Tachtigjarige Oorlog, 1573-1604 (RU Groningen, Alphen aan den Rijn: Canaletto, 1991) heeft F. Westra een interessant hoofdstuk gewijd aan ‘Ingenieurs en stadhouders’.

[p. 96]

reden’. In de eerste plaats om te voorkomen dat anderen zich de vondsten van Maurits en hem zouden toeëigenen. In de tweede plaats om buitenstaanders in de gelegenheid te stellen gemaakte fouten te verbeteren en nieuwe ontdekkingen te doen, op deze wijze kon het werk ‘ten gemeenen besten’ dienen. Een derde reden betrof Stevins idee van de ‘Wysentijt’. Sinds die vermeende ‘Wysentijt’ zou de wetenschap voortdurend achteruit zijn gegaan. Om de oude staat van ‘volcommenheyt’ weer te herstellen moeten, volgens Stevin, zoveel mogelijk mensen bij de wetenschap betrokken worden; het gebruik van ‘eyghen spraeck’ is hierbij essentieel. De Wisconstighe ghedachtenissen zouden hiertoe dan ook een bijdrage kunnen leveren.^14.

Van een drietal ‘t'saemspraecken’ die Stevin met Maurits voerde heeft hij een gedetailleerd verslag gemaakt.^15. De bescheiden omvang ervan en de onopvallende plaats in de Wiscunstighe ghedachtenissen pleiten voor een zekere natuurgetrouwheid, al kan Stevins welwillendheid hem parten hebben gespeeld. Om een indruk te krijgen van de - niet van humor gespeende - omgang tussen stadhouder en tutor hebben wij een fragment uit een ervan, de laatste, overgenomen. Deze samenspraak betreft het nut van de nieuwe manier van boekhouden, zoals die door Stevin wordt voorgestaan. De nieuwe werkwijze voorkomt dat een ‘thresorier’ zich, laten wij zeggen zijns ondanks, verrijkt ten nadele van de hem toevertrouwde schatkist. Maurits lijkt overtuigd^16.:

S.V.G. [ =syn Vorstelicke Genade]: ‘Maer ghenomen dat dese dinghen alsoo te doen waren ghelijck ment deur imaginatie sich inbeelt, nochtans souder uyt te verwachten staen, dat sulcke Bouckhouders me menschen sijnde oock cromme schermsprongen souden springen als d'ander, waermede het eintlick al op den ouden voet soude gheraken.

ST [= Stevin]: Men mocht verwachten dat de Vorsten mette Bouckhouders souden varen ghelijck de Cooplien, alwaer d'ervaring leert dat de selve Bouckhouders int ghemeen gheen schatten en vergaren, noch met ongerechticheyt in haer ampt besaemt en syn: Angaende ymant voor een gheval mocht rekenen dattet den Cooplieden nu ter tijt met hun bouckhouders wel gheluckt, ick ben van ander gevoelen, en meyne daer af de Bouckhouding een bekende oirsaeck te wesen, welcke de onrechtveerdighe menschen met ghewelt tot rechtveerdicheyt dringt, om de schaemte en vreese dieder uyt volght.

S.V.G.: Men mocht daer af oock d'oirsaeck achten dat de Cooplien gheduerlick toe sien, en me een oogh int seyl hebben.

ST: Dat helpter oock toe, en schijnt dattet de Vorsten een luttelken souden meughen navolgen, wanttet hemlien veel minder swaricheyt soude sijn, sweecx een uyr of twee tot deursichting der boucken te besteden, dan dickwils requesten van clagende Crediteurs te lesen, oock daghelicx sich te becommeren en 't hooft te breken, ghelijckt menighe ghebeurt, op wat wijse men bequamenlicxt penninghen op intrest sal lichten, en wat Landen of partien datmen eerst vercoopen sal.

S.V.G.: Ick verstae u meyning. [..]’

14. Voor de invloed die de purist Stevin zou uitoefenen op de ontwikkeling van de Nederlandse taal, zie M. van der Wal (in samenwerking met C. van Bree), Geschiedenis van het Nederlands, Utrecht, Het Spectrum, 1992, par. 7.6, 7.7 en 7.9.

15. Dr. J.C. Roling (RU Leiden) maakte mij attent op vergelijkbare dialoogliteratuur rond de persoon van Jacobus VI(I), koning van Schotland vanaf 1567 en van 1603 tot 1625 tevens koning van Engeland.

16. Stevin, ‘Van de Vorstelicke bouckhouding op de Italiaense wyse’, ‘t'saemspraeck’, p.40-44, in het bijzonder p. 42; in op. cit. (noot 5), deel II (stuk V).

[p. 97]

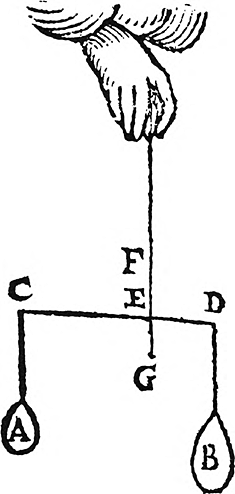
Figuur 2.

3. Zwaartepuntsbepalingen: ‘spiegheling’ en ‘daet’

In dezelfde sfeer als de ‘t'saemspraecken’ over boekhoudkunde zullen, zo mag men wel aannemen, de lessen in de theoretische en toegepaste wiskunde zijn verlopen. In het nu volgende willen wij in grote lijnen aangeven wat daar werd behandeld als voorbereiding op de oplossing van een praktisch probleem, nl. het voorkomen dat een met soldaten op ladders beladen schip topzwaar wordt en kapseist. Het bedoelde probleem wordt besproken in een in samenwerking met de Prins verzorgd ‘byvough’ bij stuk IV, De weeghconst, dat zelf volgt op De meetdaet (stuk III).^17. Men moet bedenken dat in het eerste stuk al veel driehoeksmeetkunde was behandeld. De volgorde is van betekenis: in het algemeen moet men zich volgens Stevin eerst

17. Dijksterhuis, op. cit. (noot 2), p. 144, gaat ervan uit dat het alleen om uitwerkingen van Stevin gaat. Volgens het ‘Cort begrijp’ (Stevin, De weeghconst, p. 2; in op. cit., noot 5, deel II) gaat het echter (mede?) om ‘vonden’ van Prins Maurits.

[p. 98]

bekwamen in de ‘spiegheling’, de theorie, alvorens over te gaan op de ‘daet’, de praktijk.^18. Dat de lessen inderdaad weerklank vonden blijkt niet alleen uit het genoemde ‘byvough’, maar ook uit het hier en daar ingelaste commentaar van Maurits. Zo, bijvoorbeeld, naar aanleiding van De meetdaet, boek VI, waar Stevin o.a. het verband tussen verschillende ruimtelijke figuren behandelt en de vraag hoe hun inhouden in elkaar uitgedrukt kunnen worden. Maurits maakt duidelijk het probleem te hebben begrepen en komt met een eigen algemene formulering van de betrokken stelling.^19.

Dit spelen met meetkundige grootheden beschouwde Stevin als een onmisbare inleiding op De weeghconst. Maurits zou deze hebben bestudeerd aan de hand van de eerste druk, die van 1586. In de Wisconstighe ghedachtenissen werd een verbeterde uitgave opgenomen, vergezeld van de vondsten van de bevelhebber. In de nieuwe versie opent het boek met definities van de grondbegrippen. Deze zou men kunnen samenvatten als in Fig.2.^20.

Als de gewichten A en B in Fig.2 elkaar in evenwicht houden heten zij ‘evestaltwichtig’. Hun onderlinge verhouding in gewicht zal dan zo zijn dat, in de woorden van Stevin, ‘de swaerste [..] sulcken reden tot de lichtste [heeft], als de langste erm [CE] tot de cortsten [DE]’.^21. Het ophangpunt E kan dan opgevat worden als het ‘swaerheyts middelpunt’ oftewel het zwaartepunt van het geheel: het punt waardoor elk vlak het ‘lichaem deelt in twee evestaltwichtighe deelen’.^22. In het algemeen kan men dan zeggen dat als iets opgehangen wordt aan zijn zwaartepunt, het in evenwicht verkeert en in de stand blijft die men het gaf.^23. Zodra het ophangpunt niet langer samenvalt met het ‘swaerheyts middelpunt’ verandert de stand van het geheel zodanig, dat het zwaartepunt loodrecht onder het ophangpunt uitkomt. Vanaf dat moment is er opnieuw evenwicht. Stevins Weeghconst is een wetenschap van het evenwicht, een statica. Het eerste boek houdt zich voornamelijk bezig met het evenwicht van rechthoekige en balkvormige objecten. In het tweede komen figuren aan bod waarvan het zwaartepunt minder gemakkelijk te vinden is, eerst vlakke, daarna ruimtelijke. Stevin volgt hierbij, onder verwijzing naar zijn voorgangers, een door Archimedes uitgedachte en recent door Federico Commandino (1509-1575) overgenomen werkwijze. Hij slaagt er zelfs in de vrij gecompliceerde aanpak van zijn voorgangers belangrijk te vereenvoudigen door een systematisch gebruik van wat tegenwoordig bekend staat als ‘limietovergangen’.^24. Dergelijke denkstappen bleken essentieel voor twee in de zeventiende eeuw opgekomen rekentechnieken, nl. de differentiaal- en integraalrekening. Bedoelde rekentechnieken, waaraan de namen van Isaac Newton en Gottfried Wilhelm Leibniz zijn verbonden, worden ook wel samengevat in de term ‘infinitesimaalrekening’, omdat aanvankelijk gebruik gemaakt werd van ‘oneindig kleine’ elementjes die samen bijvoorbeeld een oppervlak uitmaken. Men sprak wel van ‘indivisibilia’ of ‘meetkundige atomen’, de bouwsteentjes van een meetkundig geheel. Het probleem was nu hoe men zich moest voorstellen dat uit oneindig kleine dingen iets van waarneembare afmetingen kan zijn opgebouwd: een lijn uit punten, een vlak uit lijnen, een volume uit vlakken. Stevin ging dit probleem handig uit de weg. In een vergelijkbaar geval, de bepaling van het zwaartepunt van een vlakke figuur, had hij gewezen op het feit dat een meetkundig vlak eigenlijk helemaal geen ‘swaerheyt’, geen gewicht, heeft. Zijns inziens moet men gewicht hier ‘lijckspreuckelick’ opvatten, ‘metapho-

18. ‘Vant menghen der Spiegheling en Daet’, in het eerste boek van het Eertclootschrift, p.46-48; Stevin, op. cit. (noot 5), deel I.

19. Stevin, De meetdaet, p. 199, in op. cit. (noot 5), deel II.

20. Stevin, De weeghconst, p. 8, in op. cit. (noot 5), deel II.

21. Stevin, ibid., 1. vertooch, 1. voorstel, p. 8.

22. Stevin, ibid., Bepaling 4, p. 6.

23. Stevin, ibid., Bepaling 4, p. 6: ‘Swaerheyts middelpunt is, an t'welck het lichaem door ons ghedacht hanghende, alle ghestalt hout die men hem gheeft’.

24. Zie, bij voorbeeld, C.B. Boyer, The history of the calculus and its conceptual development, New York, Dover, 1959 (eerste druk 1939), p. 99 e.v.

[p. 99]

ricè’. Wanneer men doet alsof een vlak gewicht heeft, kan men aannemen dat de grootte van dat gewicht evenredig is met de grootte van het oppervlak, om op deze wijze tot nuttige uitkomsten te komen: ‘t'valsche wort toeghelaten opdat men t'waerachtighe daer door leere’.^25. Middels zijn ‘limietovergangen’ wist Stevin op eenvoudige wijze aan te tonen waar het zwaartepunt van de meest uiteenlopend gevormde dingen gezocht moest worden.

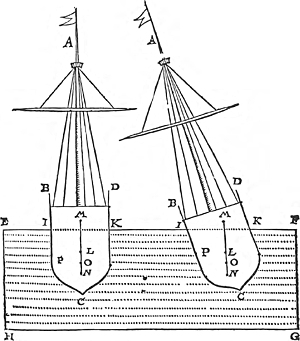
Tot zover, althans wat Stevin betreft, de ‘spiegheling’ aangaande de bepaling van zwaartepunten in het algemeen. Het praktisch belang van de kennis van zwaartepunten is groter dan men wellicht op het eerste gezicht geneigd is te denken. Een goed voorbeeld is het gedrag van een gedeeltelijk in een vloeistof ondergedompeld, drijvend ding, laten wij zeggen een schip in het water. De stabiliteit van zo'n schip wordt bepaald door de ligging van zijn zwaartepunt t.o.v. het zwaartepunt van de verplaatste hoeveelheid water. In Fig. 3 stelt L het zwaartepunt voor van een hoeveelheid water van dezelfde vorm als het ondergedompelde deel van het schip. Men kan zich nu voorstellen dat de plaats van het zwaartepunt van het schip afhangt van de plaats waar de lading wordt ondergebracht. De ervaring leert dat wanneer men een relatief zware lading boven aan de mast bevestigd, bij A, het schip ‘topzwaar’ wordt: het kleinste zetje is dan voldoende om het doen omslaan, dit omdat het zwaartepunt van het schip als geheel, inclusief die lading, boven het punt L is komen te liggen. Om het schip stabiel te maken moet men zorgen dat zijn zwaartepunt beneden L komt te liggen. Dit kan eenvoudig door de zwaarste lading op het laagste punt in het ruim te leggen. In samenwerking met Maurits komt Stevin nu tot de oplossing van een krijgskundig probleem aangaande de belading van een schip dat gebruikt moet worden als basis voor de belegering van een stad d.m.v. soldaten op ladders.^26. Door de omhoogklimmende soldaten komt het zwaartepunt van het schip immers buiten zijn as en steeds hoger te liggen: zonder maatregelen zal het schip gaan overhellen en uiteindelijk zelfs omslaan als dat zwaartepunt boven L uitkomt. De te nemen maatregel is duidelijk: de zwaarste lading moet onder in het ruim, bij C, gebracht worden. Het maximale aantal manschappen dat met behulp van ladders de belegering zonder gevaar voor omslaan kan uitvoeren kan dan ruwweg bepaald worden aan de hand van de ligging van L, de hoogte van de belegerde muur en de grootte van de lading bij C.

25. Stevin, De weeghconst, p. 60.

26. Stevin, ibid., p. 199-202, ‘Vande vlietende topswaerheyt’.

4. Slot

In het voorgaande is wel duidelijk geworden op welk hoog niveau het door Stevin verzorgde onderwijs van bevelhebber Maurits stond. Van bijzonder belang is de vereenvoudiging van de ‘topzware’ archimedische bewijsvoering, een vereenvoudiging die bestond in een intuïtieve vorm van het latere limietbegrip. Verder kan gewezen worden op het impliciete gebruik van ‘oneindig kleine’ onderdelen die door hun opeenhoping een meetkundige figuur uitmaken. In de loop van de zeventiende eeuw zouden dergelijke ‘indivisibilia’ of ‘meetkundige atomen’ een standaardonderdeel worden van het wiskundige gereedschap.^27. Het ging al spoedig niet meer om alleen zwaartepuntsbepalingen, met in hun verlengde oppervlakteen inhoudsberekeningen van meetkundige objecten. Een driehoek, rechthoek of pa-

27. Zie bij voorbeeld E. Festa, ‘La notion d' “agrégat d'indivisibles” dans la constitution de la cinématique galiléenne: Cavalieri, Galilée, Torricelli’. In: Revue d'Histoire des Sciences 45 (2-3) 307-336 (1992). Zie ook J.-M. Salanskis en H. Sinacoeur (red.), Le Labyrinthe du continu, Parijs 1992.

[p. 100]

rabool had inmiddels ook een natuurkundige betekenis gekregen, nl. als grafiek waarin het verloop van een natuurverschijnsel staat uitgedrukt. Vandaar dat zo'n ogenschijnlijk triviaal probleem als de zwaartepuntsbepaling een belangrijke rol heeft kunnen spelen, niet alleen in de wiskunde, maar ook in de natuurkunde. Het wordt ook begrijpelijk dat vele zestiende- en zeventiende-eeuwse natuuronderzoekers, naar het voorbeeld van Archimedes, zich hebben verdiept in de problemen rond dingen die op water dobberen, op dat kennelijk fascinerende grensgebied tussen natuur- en wiskunde.^28.

Het lijdt geen twijfel dat Simon Stevin door het hoge niveau van zijn lessen een inspirerende invloed heeft uitgeoefend op de culturele, de wetenschappelijke en de technische vorming van de jonge stadhouder, zo tussen diens 26e en 39e jaar. Stevins praktische instelling, zijn voorkeur voor een combinatie van ‘spiegheling’ en ‘daet’, voor ‘theorie’ en ‘praktijk’, moet Maurits hebben aangesproken. Daarnaast zullen Stevins opmerkelijke historische en taalkundige ideeën, hoe discutabel ook in onze ogen, een enthousiasmerende werking hebben gehad, niet alleen op de bevelhebber, maar op de gehele bevolking van de ‘Verenichde Nederlanden’. Wanneer zo overtuigend kon worden aangetoond dat er ooit een Wysentijt is geweest, waarin de wetenschappen op strikt euclidische grondslag beoefend werden en de voertaal het Hollands was, kon het niet anders dan dat de Opstand ook het herstel van de wetenschappen zou bevorderen, waarmee tegelijk de uiteindelijke overwinning verzekerd leek. Zo naïef - maar dan toch verfrissend! - als Stevins taalkundige en historische denkbeelden waren, zo pragmatisch en toegesneden op de situatie anno 1590 in de ‘Vereenichde Nederlanden’ waren zijn sociaal-politieke opvattingen.^29. Hoewel het werk waarin hij de laatste verwoordde, Vita politica. Het burgherlick leven, niet werd opgenomen in de Wisconstighe ghedachtenissen, mag men blijkens

28. Ook van bij voorbeeld Christiaan Huygens kent men een verhandeling De iis quae liquido supernatant [Over de dingen die op een vloeistof drijven](1650).

29. Zie het werk van C. Secretan, besproken in deze aflevering, p. 219-221.

[p. 101]

het aangehaalde fragment uit de ‘t'saemspraeck’ over het boekhouden in alle redelijkheid aannemen, dat Maurits ook in dit opzicht zeer ingenomen zal zijn geweest met de nuchtere, evenwichtige opvattingen van zijn ‘factotum’, of liever: zijn ‘aldoender’.