De Zeventiende Eeuw. Jaargang 7

[p. 7]

Christiaan Huygens en de muziek
J. van de Craats

Zou men alleen afgaan op wat Christiaan Huygens (1629-1695) aan eigen composities heeft nagelaten, dan zou een voordracht over zijn betekenis voor de muziek kort kunnen zijn: we kennen slechts één werkje van zijn hand, een onvoltooide, acht maten tellende Courante voor klavier in E-klein (fol. 52r van de Codex Hugenianus 27 van de Leidse Universiteitsbibliotheek). Toch was Huygens geen onverdienstelijke amateur-musicus: op negenjarige leeftijd ontving hij zijn eerste zanglessen van zijn vader, en spoedig daarna leerde hij ook viola da gamba, luit en clavecimbel spelen. Gedurende zijn hele verdere loopbaan toonde hij een actieve belangstelling voor de muziek en het muziekleven van zijn tijd. En het spreekt daarbij haast vanzelf dat hij zich als wis- en natuurkundige ook bezighield met de theoretische grondslagen van de muziek en de praktische problemen op muziektheoretisch gebied die in die tijd in het centrum van de belangstelling stonden. Die problemen hadden vooral betrekking op de octaafverdeling en de stemmingswijze van toetsinstrumenten. Huygens' belangrijkste inzichten en ontdekkingen op dit terrein zijn vervat in de in 1691 in het tijdschrift Histoire des Ouvrages des Sçavans gepubliceerde Lettre de Mr. Huygens à l'Auteur touchant le Cycle Harmonique. De Auteur uit de titel is de uitgever van het tijdschrift, Henri Basnage de Beauval, een naar de Nederlanden gevluchte hugenoot. We zullen in het vervolg ingaan op de inhoud van Huygens' invloedrijke brief - het betreffende tijdschriftnummer werd driemaal herdrukt, en een vertaling ervan in het Latijn door Willem Jacob 's-Gravesande verscheen in 1724 onder de titel Novus cyclus harmonicus - en enige woorden wijden aan de betekenis van Huygens' muziektheoretische werk voor de muziekgeschiedenis.

Toonhoogte en frequentie

De banden tussen de muziek en de natuurwetenschappen, van oudsher al nauw en intensief, waren juist in de zeventiende eeuw weer extra aangehaald door de ontdekking dat de hoogte van een toon evenredig is met de frequentie van de trilling welke die toon veroorzaakt, en door onderzoek naar de trillingswijze van gespannen snaren en luchtkolommen in orgelpijpen en blaasinstrumenten. Op deze manier verkreeg men een natuurwetenschappelijke verklaring voor de reeds uit de tijd van Pythagoras stammende observatie, dat welluidende muzikale intervallen corresponderen met eenvoudige getalsverhoudingen: verdeelt men een gespannen snaar in twee delen met een eenvoudige lengteverhouding, dan zullen de stukken, als men ze aantokkelt of aanstrijkt, tonen laten horen die tezamen een welluidende indruk maken. Een lengteverhouding 2:1 correspondeert daarbij met een octaaf, 3:2 geeft een kwint, 4:3 een kwart en 5:4 een grote terts, om slechts de belangrijkste intervallen te noemen.

[p. 8]

Op fysische gronden was duidelijk geworden dat de lengteverhouding van de twee snaardelen omgekeerd evenredig is met de frequentieverhouding van de betreffende snaartrillingen, en zo heeft men dus voor het octaaf, de kwint, de kwart en de grote terts achtereenvolgens de frequentieverhoudingen 1:2, 2:3, 3:4 en 4:5. Dat zulke intervallen welluidend klinken, correspondeert met het ‘in de pas lopen’ van de trillingen als gevolg van het feit dat de frequenties een eenvoudige getalsverhouding hebben. Het octaaf (1:2) is daarbij het meest welluidende interval: tonen die een octaaf verschillen, versmelten zozeer, dat je ze nauwelijks van elkaar kunt onderscheiden als je ze tegelijk hoort, zo goed past de hoge toon (met dubbele frequentie) bij de lage. Als mannen en vrouwen dezelfde melodie zingen, zullen de vrouwen meestal een octaaf hoger zingen dan de mannen. In het muziekschrift worden tonen die een octaaf verschillen ook met dezelfde letter (toonnaam) aangeduid.

De intervallen kwint (2:3) en kwart (3:4) zijn eveneens zeer welluidend. In zekere zin zijn ze aan elkaar verwant, want als je bij de kwint de laagste toon een octaaf omhoog haalt (dat wil zeggen de frequentie ervan verdubbelt), krijg je een kwart. Kwinten en kwarten spelen in de muziek van alle volkeren een dominerende rol. Ook de grote terts (4:5) is uit onze muziek niet weg te denken. We vinden dat interval samen met de kwint terug in de grote-tertsdrieklank, een samenklank van drie tonen in de verhouding 4:5:6, die de afgelopen eeuwen de harmonische ruggegraat is gaan vormen van het overgrote deel van onze westerse muziek (de buitenste twee tonen van zo'n drieklank vormen een kwint, want 4:6 = 2:3).

Het ligt voor de hand ook andere eenvoudige getalsverhoudingen te bezien, bijvoorbeeld verhoudingen waarin het getal 7 een rol speelt zoals 4:7, 5:7 en 6:7. In hoeverre muzikale intervallen met deze verhoudingen in onze muziek een rol spelen, is onder musicologen nog steeds een strijdpunt. Traditioneel hield men ze buiten de theorie, maar de wiskundige Leonhard Euler (1707-1783) stelde al dat de welluidendheid van het zg. dominant-septiemakkoord, dat na de grote-tertsdrieklank het belangrijkste akkoord in onze westerse harmonie is geworden, berust op het feit dat de frequentieverhouding van de vier tonen die erin voorkomen vrijwel gelijk is aan 4:5:6:7. Het is in dit verband interessant om te vermelden wat Huygens schreef over de intervallen 5:7 en 7:10 (Oeuvres Complètes xx, p. 161):

Nu zeg ik dat deze intervallen van 7 tot 5 en van 10 tot 7 iets harmonieus hebben, als men ze aandachtig keurt (althans zo bevind ik het met mijn oor) en dat men ze onder de consonanten zou kunnen rekenen, wat ook de meesters componisten daarvan willen zeggen, die ze integendeel onder de valse betrekkingen rangschikken.

Verderop merkt Huygens nog op dat deze intervallen vrijwel zuiver voorkomen in de middentoonstemming, de in die tijd meest gebruikelijke wijze om toetsinstrumenten te stemmen.

De middentoonstemming

Met welluidende intervallen als bouwstenen kan men toonsystemen vormen: stelsels tonen die allemaal via zulke intervallen met elkaar in verband staan. Als men zo te werk gaat, stuit men echter al snel op het tertsenprobleem, een stemmingspro-

[p. 9]

bleem dat in zijn eenvoudigste vorm als volgt kan worden weergegeven. Uitgaande van een toon C kom je na vier kwinten omhoog en daarna weer twee octaven omlaag op een toon E terecht die bijna, maar net niet helemaal, gelijk is aan de toon E die je krijgt door direct vanuit C een grote terts omhoog te gaan. Figuur 1 illustreert de situatie.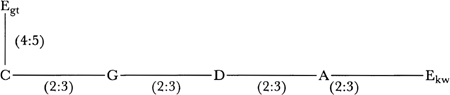

Figuur 1: het tertsenprobleem

(De octaafsprongen omlaag hebben we in dit schema weggelaten; octaafverschillen zullen we in het vervolg steeds buiten beschouwing laten.) Voor de duidelijkheid zijn de twee verschillende tonen E van indices voorzien om ze van elkaar te onderscheiden: E_kw voor de toon E die via vier kwintsprongen bereikt wordt, en E_gt voor de toon E die een grote terts boven de C ligt. De frequentieverhouding van de tonen C en E_kw krijg je door eerst vier kwintsprongen in rekening te brengen, hetgeen leidt tot een verhouding (2:3)⁴ = 16:81, en vervolgens die toon twee octaven omlaag te halen, waardoor de verhouding C:E_kw = 64:81 ontstaat. Dat is bijna, maar niet helemaal, gelijk aan de zuivere grote terts C:E_gt = 4:5 = 64:80. De toon E_gt van de zuivere grote terts ligt iets lager dan de toon E_kw. Die laatste toon klinkt samen met de C ‘vals’: je kunt zwevingen horen als je ze tegelijk laat klinken. Dat geeft stemmingsproblemen bij een toetsinstrument met slechts 12 toetsen per octaaf. In dat geval zal je een keuze moeten doen, want er is op zo'n klavier maar plaats voor één toets E. Stem je het instrument met behulp van zuivere kwinten, dan worden de grote tertsen vals; wil je daarentegen een zuivere grote terts, dan kunnen niet alle kwinten zuiver zijn.

Men heeft daarom naar compromissen gezocht, en in Huygens' tijd was de meest gebruikelijke oplossing de middentoonstemming, een stemmingswijze waarbij men de vier kwinten alle vier in dezelfde mate een klein beetje verkleint (‘tempereert’), met als resultaat dat de toon E_kw gelijk wordt aan de zuivere grote-tertstoon E_gt. De toon D komt dan precies midden tussen de C en de E te liggen, vandaar de naam van dit systeem. Heb je eenmaal op deze wijze een ‘skelet van tonen’ gestemd volgens het schema van figuur 2, waarbij de door stippellijnen aangegeven ‘kwinten’ een heel klein beetje kleiner gemaakt zijn (het verschil is zo klein, dat je het nauwelijks hoort, en zeker niet als

[p. 10]

storend ervaart), dan kun je het via zuivere grote tertsen uitbreiden tot een systeem van twaalf tonen per octaaf (figuur 3).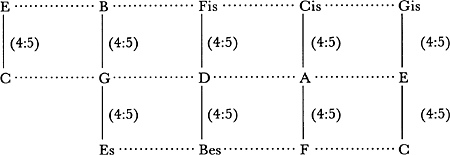

Figuur 3: de middentoonstemming

De tonen E en C komen in figuur 3 twee maal voor; de kwinten worden echter juist zo veel kleiner gemaakt dat die tonen gelijk worden. Stem je een clavecimbel op deze wijze, dan krijg je dus een toonsysteem met acht zuivere grote-tertsintervallen en elf bijna-zuivere kwintintervallen. Toch heeft dit stelsel ook z'n nadelen. Omdat het een ongelijke octaafverdeling behelst, is het interval Gis-Es, dat er op het klavier uitziet als een kwint, hinderlijk vals (het is een zg. ‘wolfskwint’: door de zwevingen lijkt het alsof je een wolf hoort huilen!). En hetzelfde geldt voor de vier overblijvende ‘grote tertsen’ B-Es, Fis-Bes, Cis-F en Gis-C (zie figuur 4).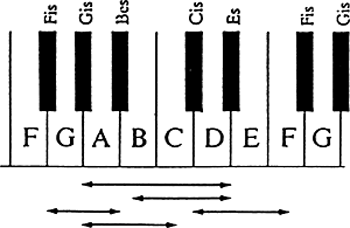

Figuur 4: valse intervallen op het klavier

Deze intervallen zal men dus bij het spelen op zo'n instrument proberen te vermijden. En als men toch in een toonsoort wil spelen waarin zulke intervallen veelvuldig voorkomen, dan moet men het hele systeem als het ware ‘opschuiven’, waardoor andere intervallen weer vals worden. De middentoonstemming is dus alleen maar bruikbaar voor een beperkt aantal toonsoorten; men kan niet onbeperkt transponeren.

[p. 11]

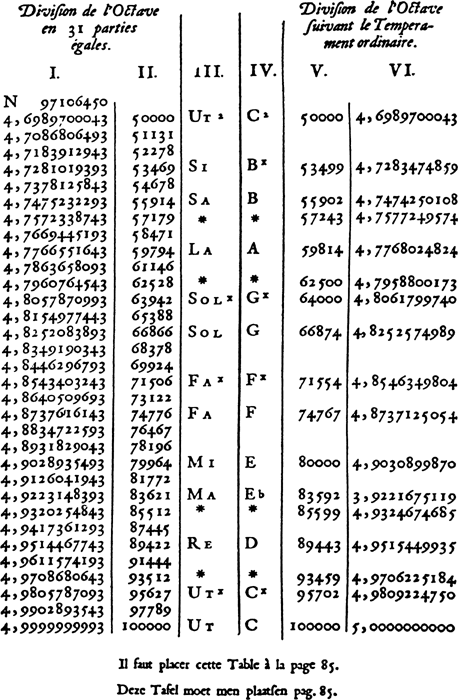
Het monochord

Het is mogelijk om aan de hand van het schema van figuur 3 de frequenties van alle tonen uit te rekenen, wanneer men de frequentie van één toon, bijvoorbeeld de C, als uitgangspunt neemt. De acht grote tertsen uit het schema hebben allemaal de ‘zuivere’ verhouding 4:5, en de voor verkleinde kwinten moet men als verhouding 1:5¼ nemen, dat is ongeveer 66874:100000 (deze verhouding zullen we nog tegenkomen in de aan Huygens' Lettre ontleende figuur 5). Aan de hand van het schema van de middentoonstemming kun je dan de frequenties van alle tonen berekenen. Maar je kunt alles ook vertalen in termen van verhoudingen van snaarlengten. Een geschikt hulpmiddel daarbij is het monochord, een enkele snaar die langs een schaalverdeling is gespannen, voorzien van een verplaatsbare kam waarmee je de lengte van het stuk dat trilt kunt variëren. Op de schaalverdeling geef je de plaatsen aan waar je de kam moet plaatsen om bepaalde tonen te krijgen. In kolom V van figuur 5 zijn de schaalwaarden van zulke punten aangegeven, met in de kolommen III en IV de bijbehorende toonnamen. De lengte van de gehele snaar is daarbij op 100000 gesteld, en het monochord is zo gestemd dat bij de hele snaar de toon C hoort (zie onderaan de kolom). De halve snaar (lengte 50000) geeft dan de C die een octaaf hoger ligt (de C² bovenaan de kolom). Daartussenin vinden we de elf andere tonen van de middentoonstemming die binnen dit octaaf liggen: B^x (onze B), B (onze Bes), A, G^x (Gis), G, F^x (Fis), E, Es, D en C^x (Cis), en ook nog een paar extra tonen die ontstaan als je het schema van figuur 3 nog wat verder uitbreidt (de zg. enharmonische tonen): Ais, As, Dis en Des (aangegeven met sterretjes). Hoe berekende Huygens die snaarlengten? Bij sommige tonen is dat gemakkelijk: de E is een zuivere grote terts boven de C, dus dat geeft een snaarlengte van (⅘) · 100000 = 80000. En de Gis ligt daar weer een zuivere grote terts boven: (⅘) · 80000 = 64000. Maar de andere tonen geven meer problemen, want daarbij krijg je te maken met ingewikkelde uitdrukkingen met de vierdemachtswortel uit 5 erin. Huygens wist echter dat zulke berekeningen veel eenvoudiger worden als je gebruik maakt van logaritmen. Dat destijds betrekkelijk nieuwe hulpmiddel (de beroemde logaritmetafel van Adriaan Vlacq in tien decimalen dateert van 1628) zet vermenigvuldigen en delen om in optellen en aftrekken, hetgeen de berekeningen sterk vereenvoudigt. De laatste kolom van figuur 5 bevat dan ook de logaritmen van de snaarlengten. In zijn brief legt Huygens uit hoe hij eraan gekomen is en hoe ermee gerekend moet worden. Hij besluit zijn tekst met de zinsnede: ‘... n'y ayant rien de si commode que les logarithmes pour ces calculs de Musique.’ (er is niets zo handig bij muzikale berekeningen als het gebruik van logaritmen).

31 tonen per octaaf

Maar het eigenlijke nieuws van Huygens' brief was niet deze berekening van de snaarlengten van de middentoonstemming, doch zijn ontdekking dat bij een verdeling van het octaaf in 31 gelijke deelintervallen de 12 tonen van de middentoonstemming bijna volmaakt tevoorschijn komen. Stem je een rij van 32 snaren op zo'n manier dat de frequentieverhouding tussen elk tweetal opvolgende snaren gelijk is, terwijl de eerste snaar een octaaf hoger gestemd is dan de laatste (zodat

[p. 12]

[p. 13]

het octaaf op die manier dus in 31 gelijke delen verdeeld wordt), dan geven de snaren met de nummers 1, 4, 6, 9, 12, 14, 17, 19, 22, 24, 27, 30, 32 vrijwel precies de tonen C², B, Bes, A, Gis, G, Fis, F, E, Es, D, Cis en C van de middentoonstemming (naar dalende toonhoogte gerangschikt). Ook dat kon Huygens met behulp van logaritmen vaststellen. Gelijke verhoudingen van snaarlengten geven namelijk gelijke verschillen van de bijbehorende logaritmen, en wat Huygens dus deed, was de logaritme van de octaafverhouding 2:1 in 31 gelijke delen verdelen. Hij legt het zelf als volgt uit:^1.

[Ik heb] de logaritme van 2, die 0,30102999566 is, door 31 gedeeld, hetgeen het getal N = 0,0097106450 oplevert, dat ik steeds opgeteld heb bij de logaritme van 50000, die 4,6989700043 is; en van die optellingen zijn de logaritmen van de [eerste] kolom afgeleid, tot aan de grootste, 4,9999999993, die, doordat deze zo weinig van 5,0000000000 (welk getal daarvoor in de plaats gesteld kan worden) verschilt, laat zien dat de berekening goed is uitgevoerd. Zij die de logaritmen begrijpen, weten dat men zo tewerk moet gaan als men dertig middelevenredigen wil hebben tussen 100000 en 50000.

Hiermee zijn ook de eerste twee kolommen van figuur 5 verklaard: de eerste kolom bevat de aldus berekende logaritmen van de snaarlengten van deze evenredige 31-toonsstemming, en de tweede kolom bevat die snaarlengten zelf.

1. [4], p. 172.

Transponeren

Het voordeel van zo'n evenredige octaafverdeling is de mogelijkheid om onbeperkt te kunnen transponeren. Men kan elke toon als ‘grondtoon’ nemen: de overeenkomstig getransponeerde selectie van 12 van de 31 tonen geeft de ‘middentoonstemming’ welke bij die grondtoon past. Maar het nadeel is natuurlijk dat een klavier van 31 toetsen per octaaf erg onpraktisch is. Huygens zegt dit zelf ook, en hij stelt daarom voor een soort clavecimbel te bouwen met weliswaar 31 snaren per octaaf, maar daarboven een verplaatsbaar 12-toetsenklavier met aan de onderzijde van de toetsen pennen die de gewenste selectie van 12 snaren bedienen. Een getransponeerd systeem zou men dan kunnen verkrijgen door het klavier te verschuiven, waardoor de pennen boven een andere twaalftal snaren terecht komen.

In Huygens' tijd is dit ontwerp waarschijnlijk nooit uitgevoerd, maar de fysicus A.D. Fokker heeft kort na de oorlog een 31-toonsorgel laten bouwen, niet met een verplaatsbaar klavier, maar met een toetsenbord met 31 toetsen per octaaf naast en boven elkaar, zo ongeveer als bij de toetsen van een schrijfmachine. Daarnaast heeft het orgel ook een ‘gewoon’ klavier van 12 toetsen, waarmee naar keuze een selectie uit de 31 tonen gemaakt kan worden, bijvoorbeeld Huygens' benadering van de middentoonstemming. Het orgel bevindt zich in Teylers Museum in Haarlem, en het wordt nog geregeld bespeeld.

Huygens' invloed op de muziektheorie

We hebben al vermeld dat Huygens' Lettre gretig aftrek vond bij zijn tijdgenoten. Dat zal zeker verband hebben gehouden met de grote wetenschappelijke reputatie van de auteur, maar minstens evenzeer met de glasheldere stijl waarin het stuk ge-

[p. 14]

schreven is. Ook nu nog is het een plezier om het te lezen, in de originele versie in het Frans, in de Latijnse vertaling van 's-Gravesande, of in de Engelse of de Nederlandse vertalingen ervan die kort geleden door dr. R.A. Rasch zijn gepubliceerd. Huygens' voorstel om de 31-toonsstemming als uitgangspunt te nemen voor de muziektheorie heeft in zijn tijd ook wel weerklank gevonden, zoals bijvoorbeeld blijkt uit een tekening ervan in de Elementa musica (Den Haag, 1739) van de organist Quirinus van Blankenburg (1654-1739) (zie figuur 6). Hij plaatste de 31 tonen van Huygens' systeem langs de omtrek van een cirkel, en verbond ze door lijnen volgens de ‘grote tertsen’ (die in Huygens's systeem vrijwel zuiver worden weergegeven). Je zou kunnen spreken van een grote-tertsencirkel, naar analogie van de kwintencirkel die bij de evenredige twaalftoonsstemming behoort. Van Blankenburg gaf zijn prent de titel ‘De Wet der Nature die alle Klanken regeleert’. De acht grote tertsen die bij de middentoonsstemming zuiver gestemd worden (vgl. figuur 3), tekende hij met dikke lijnen.

Maar al snel daarna verdween de 31-toonsstemming vrijwel helemaal van het toneel, totdat A.D. Fokker haar in de veertiger jaren van onze eeuw herontdekte. Hij werd een warm pleitbezorger van het systeem, maar daarbij gebruikte hij het op een wijze die Huygens' oorspronkelijke bedoelingen verre oversteeg. Was de 31-toonsstemming voor Huygens vooral een middel om de middentoonsstemming in alle mogelijke transposities te kunnen spelen, voor Fokker was het een stelsel dat ongekende nieuwe muzikale mogelijkheden in zich droeg. Hij dacht daarbij aan nieuwe toonsystemen die gevormd werden op een wijze die al door Euler was aangegeven, en waarbij hij naast het octaaf, de kwint en de grote terts ook het ‘septimale’ interval 4:7 als bouwsteen gebruikte. In zekere zin was Huygens hierop al vooruit gelopen toen hij opmerkte dat de intervallen 5:7 en 7:10 vrijwel zuiver in de middentoonsstemming aanwezig zijn. Als gevolg daarvan vindt men de septimale intervallen ook in een zeer goede benadering in de 31-toonsstemming terug.

31 versus 12

Voor Huygens was de middentoonsstemming de ‘juiste’, ‘natuurlijke’ wijze om toetsinstrumenten te stemmen. Zoals veel van zijn tijdgenoten stelde Huygens deze stemmingswijze boven alle andere compromisstemmingen, waarvan er overigens vele in omloop waren. De thans gebruikelijke evenredige twaalftoonsstemming, waarbij het octaaf in twaalf gelijke deelintervallen verdeeld wordt, was destijds ook wel bekend,^2. maar ze werd door vrijwel alle musici verworpen. In die stemming zijn de kwinten bijna zuiver, maar de grote tertsen zijn hoorbaar vals, en dat vond men destijds een onoverkomelijk bezwaar. Zoals we al opgemerkt hebben ontwierp Huygens zijn 31-toonsstemming dus vooral als een hulpmiddel om transposities gemakkelijk te maken. Het cyclische karakter van zijn systeem, dat wil zeggen het feit dat alle 31 deelintervallen van het octaaf even groot zijn, maakt dat je onbeperkt kunt transponeren. En de afwijkingen van de middentoonsstemming zijn zo gering dat ze zelfs voor het scherpste gehoor niet zijn waar te nemen.

Niets wijst er echter op dat Huygens zijn systeem ook ontworpen zou hebben om onbeperkt modulaties, dat wil zeggen overgangen binnen een muziekstuk naar een andere toonsoort, mogelijk te maken, of dat hij zulks ook maar overwogen

2. Zie hiervoor bijvoorbeeld het artikel van Cohen [1].

[p. 15]

heeft. Dat zou ook een anachronisme zijn geweest: een muziekstuk stond in een bepaalde toonsoort; in zo'n toonsoort gebruikte je maar een beperkt aantal tonen (zeker niet meer dan twaalf per octaaf), en de stemming van het instrument werd bij die toonsoort aangepast.

Maar in de achttiende eeuw, en nog veel meer in de negentiende eeuw, gingen de componisten de toonsystemen steeds verder uitbreiden. Daarnaast ging men ook steeds vrijer moduleren, waardoor de beperkingen van de middentoonsstemming (en andere ongelijke octaafverdelingen) als steeds knellender werden ervaren. Omdat tegelijkertijd het klavier met twaalf toetsen per octaaf zich ontwikkelde tot de standaard voor toetsinstrumenten, terwijl componisten en virtuozen er ook telkens weer nieuwe uitdrukkingsmogelijkheden voor vonden, veroverde de oc-

[p. 16]

taafverdeling in twaalf gelijke deelintervallen meer en meer terrein. De valse grote tertsen die zo'n verdeling met zich meebrengt, en die voor Huygens en zijn tijdgenoten nog een reden waren om die stemmingswijze te verwerpen, nam men daarbij op de koop toe. Zo verdween de middentoonsstemming geleidelijk van het toneel, en daarmee verdween ook een belangrijke bestaansgrond van Huygens' systeem.

Verantwoording: Veel informatie voor dit artikel heb ik ontleend aan [4]; ook de figuren 5 en 6 zijn hieruit afkomstig. Figuur 4 is uit [2]; daarin vindt men ook meer over andere evenredige octaafverdelingen.

Literatuur

1.	H. Floris Cohen. ‘Simon Stevin's Equal Division of the Octave’. In: Annals of Science 44 (1987), p. 471-488.
2.	Jan van de Craats. De Fis van Euler. Aramith Uitgevers. Bloemendaal 1989.
3.	Christiaan Huygens. Oeuvres Complète. 22 vols. Den Haag, 1888-1950.
4.	Christiaan Huygens. Le cycle harmonique (Rotterdam 1691) Novus cyclus harmonicus (Leiden 1724) with Dutch and English translations. Edited by Rudolf Rasch. Diapason Press. Utrecht 1986.