De Zeventiende Eeuw. Jaargang 7

[p. 17]

Mathematische uitgangspunten van de Hollandse bouwkunst in de 17de eeuw^1.
K.A. Ottenheym

Het humanistische ideaal

Vanoudsher hebben architecten gebruik gemaakt van mathematische principes om in het hoofd bedachte ontwerpen concreet gestalte te geven en vorm en maat hiervan te bepalen.^2. In de classicistische architectuur van de 17de eeuw in Holland was het gebruik van zuivere maatverhoudingen daarbij van het grootste belang in het streven naar de perfecte schoonheid. Deze opvatting was, zoals bekend, geënt op het geschrift van Vitruvius uit de tijd van keizer Augustus, De Architectura Libri Decem, en de Italiaanse verwerking van deze theorie uit de 15de en 16de eeuw. Leon Battista Alberti stelde in zijn De Re Aedificatoria dat de eerste schoonheid van de architectuur bepaald werd door de harmonie van de maten van een gebouw.^3. Zuilenorden waren in zijn ogen slechts decoratie en konden samen met andere versieringen als tweede, toegevoegde schoonheid worden gebruikt, in zekere zin om de inwendige harmonie van een gebouw voor het oog afleesbaar te maken. Op deze wijze kon men in de architectuur een objectieve en perfecte schoonheid nastreven. Met behulp van zuivere proporties volgde men immers volgens deze humanistische theorieën de goddelijke schoonheid zoals die overal in de Schepping terug te vinden is, zoals in de maten van de mens, de afstanden van de planeten en vooral in de muziek.^4.

Na de cirkel en het vierkant zijn volgens Vitruvius en de Italiaanse tractaatschrijvers 3:4, 2:3, 3:5 en 1:2 de belangrijkste proporties voor de architectuur. Deze getalsverhoudingen waren immers sedert Pythagoras onlosmakelijk verbonden met de zuivere muzikale intervallen terts, kwart, kwint en octaaf.^5. Daarnaast noemden Vitruvius en de latere schrijvers ook de verhouding van 1:√2 van groot belang voor de architectuur. De verhouding 1:√2 is die van de zijde van een vierkant van 1×1 tot zijn diagonaal en is slechts meetkundig voor te stellen. De rekenkundige equivalent van deze verhouding zal altijd een benadering zijn, gezien het feit dat √2 een ‘irrationeel’ getal is. Als bruikbare benadering van deze verhouding gebruikte men de rekenkundige proportie 5:7. De wortelverhouding 1:√2 was ook in de middeleeuwse bouwwereld in heel Europa als vuistregel in gebruik gebleven.^6. Bij de hernieuwde belangstelling voor de klassieke architectuur werd de 1:√2-verhouding probleemloos in de harmonische proportiereeks ingevoegd, zoals Vitruvius reeds had aangegeven.^7. Ook in de 17de-eeuwse architectuur in Holland is deze verhouding veelvuldig samen met de harmonische getalsverhoudingen toegepast.

De humanistische idealen over de perfecte schoonheid in de architectuur bereikten Holland, zoals bekend, omstreeks 1625 via de Italiaanse tractaten van Palladio en Scamozzi, I Quattro Libri dell' Architettura (Venetië 1570) en L'Idea dell' Architettura Universale (Venetië 1615). Van beide boeken verschenen in de 17de eeuw Nederlandse edities, waarbij het werk van Scamozzi duidelijk grotere belangstelling genoot dan dat van Palladio.^8. In de eerste decennia van de 17de eeuw was alle aan-

1. Zie voor een gedetailleerde behandeling van dit onderwerp: K.A. Ottenheym. Philips Vingboons (1607-1678), architect. (Diss. Leiden 1989) Zutphen 1989, pp. 153-172 (hoofdstuk 8, ‘Philips Vingboons en de architectuurtheorie’).

2. P.H. Scholfield. The Theory of Proportion in Architecture. Cambridge 1958. P. von Naredi-Rainer. Architektur und Harmonie. Keulen 1982. In uitzonderlijke gevallen werd aan de gebruikte getallenreeksen, die in eerste instantie als hulpmiddel bij het ontwerp dienden, ook bijzondere betekenis gehecht. De verhouding die men als ‘de gulden snede’ pleegt aan te duiden is in de architectuurpraktijk slechts bij zeer hoge uitzondering toegepast. Meestal wanneer men meent deze verhouding, die alleen geometrisch is voor te stellen, op het spoor te zijn, gaat het in werkelijkheid om de zuiver rekenkundige verhouding 3:5, die direkt deel uitmaakt van de harmonieuze getallenreeks (zie noot 5 hieronder).

3. L.B. Alberti. De re aedificatoria. Florence 1485.

4. Zie het baanbrekende werk van R. Wittkower. Architectural Principles in the Age of Humanism. Londen 1949¹.

5. Pythagoras had het directe verband tussen zuivere intervallen en zuivere getalsverhoudingen in de snaarlengten vastgesteld, zoals 3:4 (terts), 2:3 (kwart), 3:5 (kwint), 1:2 (octaaf). Zie voor de toepassing hiervan in de architectuur Wittkower 1949 (zie noot 4), hoofdstuk 4, ‘The Problem of harmonic Proportion in Architecture.’.

6. De gotische quadratuur is geheel gebaseerd op √2-verhoudingen. Zie hiervoor: R. Shelby (ed.). Gothic Design Techniques. Carbondale, Edwardsville 1977.

7. Vitruvius. De Architectura Libri Decem, Lib. vi. cap. 3. Vitruvius adviseert hier voor de afmetingen van een atrium in een particulier huis de verhoudingen 3:5, 2:3 of 1:√2.

8. J.J. Terwen. ‘Mag de architectuur van het Hollands Classicisme “Palladiaans” genoemd worden?’ In: Nederlands Kunsthistorisch Jaarboek 33 (1983), pp. 169-189.

[p. 18]

dacht gericht op uitbundige en fantasievolle geveldecoraties met allerhande renaissance-ornamenten, zonder kenbare belangstelling voor de theoretische achtergronden van deze vormenschat. In de jaren '20 ontwikkelden echter enkele kunstenaars uit Haarlem, waaronder Jacob van Campen en Salomon de Bray, een andere bouwstijl, geïnspireerd op het classicisme uit Noord-Italië van Palladio en Scamozzi. Vooral Constantijn Huygens en zijn kring golden vanaf de jaren '30 van de 17de eeuw als voorstander en stimulator van de classicistische architectuuridealen.^9. Diens huis aan het Plein (1634) en het Mauritshuis (1633) in Den Haag zijn de bekende vroege voorbeelden van deze architectuur.^10. Het ornament werd hierbij beperkt tot de klassieke pilasterorden en ingepast in een streng mathematisch stramien dat ook door het muurwerk en de vensters werd gevolgd. Door het werk van architecten als Jacob van Campen, Pieter Post, Philips Vingboons en Arent van 's-Gravesande zou het classicisme het gezicht van de Holland in de 17de eeuw in grote mate gaan bepalen.

9. Zie voor de Vitruviusstudie in de 17de eeuw in Holland: A. Bodar. ‘Vitruvius in de Nederlanden.’ In: Bouwen in Nederland (Leids Kunsthistorisch Jaarboek 3), Delft 1985, pp. 63-69.

10. Zie voor het huis van Huygens: G. Kamphuis. ‘Constantijn Huygens, bouwheer of bouwmeester?’ In Oud Holland 77 (1962), pp. 151-180. Zie voor het Mauritshuis: E. van den Boogaart (red.). Johan Maurits van Nassau-Siegen 1604-1679. A Humanist Prince in Europe and Brazil. Den Haag 1979.

Nederlandse architectuurboeken in de eerste helft van de 17de eeuw

In de 17de eeuw bestond er geen opleiding tot architect als zodanig. Het ontwerpen van gebouwen was een specialisatie die men vanuit verschillende richtingen kon bereiken, zoals de teken- en schilderkunst, beeldhouwkunst, timmer- en steenhouwersambacht, landmeetkunde en vestingbouw. Een gedegen kennis van mathematiek was hierbij het gezamenlijke uitgangspunt. Vooral in de vestingbouw en landmeetkunde was het werken op zuiver mathematische grondslag reeds vanaf de tijd van Prins Maurits en Simon Stevin tot principe verheven. Vanuit de vestingbouw en de landmeetkunde bereikte de toepassing van de wiskunde in de Republiek in het begin van de 17de eeuw ook de architectuur. Met name bij de stadsuitbreidingen en het uitzetten van de bouwpercelen raakten deze disciplines elkaar.^11. De eerste Nederlandse architectuurtractaten in de 17de eeuw, die vóór de vertalingen van de Italiaanse werken verschenen, zijn dan ook in één reeks met de vestingbouw en landmeetkunde verschenen. Evenals in de Italiaanse tractaten van ondermeer Palladio en Scamozzi gold in deze boeken het werken op mathematische grondslag als uitgangspunt. De humanistische idealen komen hierin minder nadrukkelijk naar voren terwijl het practische nut van de mathematische werkwijze alle aandacht krijgt.

In 1617 verscheen in Amsterdam het omvangrijke werk van Samuel Marolois, Opera Mathematica ou Oeuvres Mathématiques, traictans de Géometrie, Perspective, Architecture et Fortification.^12. In dit boek geldt de wiskunde, en vooral de geometrie, als uitgangspunt voor de perspectiefleer, architectuur en vooral voor de vestingbouw. De verschillende onderdelen van dit boek verschenen weldra in verbeterde Nederlandstalige edities, bewerkt door Hondius, zoals in 1628 Architectuur, dat is Bouwkunde.^13. In navolging van Vitruvius en alle tractaatschrijvers van de renaissance, noemt de schrijver de verschillende wetenschappen die voor de architectuur vereist zijn. Dat zijn ondermeer de geometria (meetkunde) voor een goed gebruik van de passer en de waterpas en de arithmetica (rekenkunde) waarmee de kosten en de maten berekend kunnen worden en de ‘zware kwestie van simmetrie’, de zuivere proportionering, kan worden opgelost. De architect moet binnen het bouwproject

11. Zie voor de nauwe samenhang tussen deze beroepen: U. Schütte e.a. (red.). Architekt und Ingenieur. Baumeister in Krieg und Frieden. (Catalogus) Wolfenbüttel 1984. Zie voor de activiteiten van de landmeters in Holland o.a. E. Taverne. In het land van Belofte, in de nieue stadt. Maarssen 1978 en E. Muller, K. Zandvliet (red.). Admissies als landmeter in Nederland voor 1811. Alphen aan den Rijn 1987.

12. Verschenen bij Jan Jansz, Amsterdam 1617.

13. Verschenen bij Jan Jansz, Amsterdam 1628.

[p. 19]

voor alle zaken de juiste maat, vorm, plaats en het juiste aantal geven en is daardoor de supervisor van alle bouwambachten. Vanwege de mathematische grondslag die hierbij onmisbaar is, wordt de architectuur in dit geschrift boven het ambacht verheven tot wetenschap. Op de titelpagina van Marolois is Vitruvius dan ook opgenomen in de geleerde kring van Euclides, Archimedes en Vitellius.

In 1631 verscheen in Amsterdam de Architectura Moderna, een verzameling gravuren met de voornaamste ontwerpen van Hendrick de Keijser (die tien jaar daarvoor was overleden) en enkele werken van Jacob van Campen en anderen.^14. Salomon de Bray schreef het voorwoord bij deze uitgave waarin hij nogmaals benadrukte dat de ware bouwkunst alleen op basis van gedegen kennis van mathematiek mogelijk is.^15. Tot slot van zijn voorrede gaf De Bray aan op welke wijze de ontwerpen bestudeerd moesten worden, namelijk door de prenten na te meten en zo de gebruikte maatverhoudingen te beproeven: de lezer wordt uitgenodigd

naer zijn welgevallen en eygen selfs oordeel deze onzetijtsche Gebouwen bij die van de Ouden [te] vergelijcken ende de selve met de ware redenen der Wis-konstighe Bouwinge [te] proeven ende naer [te] meten.

Een vergelijkbare opzet vindt men zeventien jaar later in de Afbeelsels van de voornaemste Gebouwen uyt alle die Philips Vingboons geordineert heeft uit 1648.^16. Vingboons bundelde hier een grote hoeveelheid van zijn eigen al dan niet uitgevoerde ontwerpen en presenteerde deze in zijn inleiding als goede voorbeelden van ‘ware Bouwkunst op maet en regelen der Ouden’, die hij in zijn eigen tijd zag opbloeien. Welke ‘maat en regelen’ hij zelf toepaste komt niet ter sprake, echter niet omdat hij dat als beroepsgeheim wilde bewaren maar omdat de mathematische ontwerpsystemen toen zo algemeen bekend waren dat daar geen verdere uitleg bij nodig was.

14. S. de Bray (inleiding). Architectura Moderna ofte Bouwinge van onsen tyt. C. Danckerts, Amsterdam 1631.

15. E. Taverne. ‘Salomon De Bray's Architectura Moderna: Biography and manifesto.’ Inleiding bij Architectura Moderna (facsim. editie). Soest 1974.

16. Verschenen bij Philips en Johannes Vingboons en Joan Blaeu, Amsterdam 1648.

Matenstelsels in de 17de-eeuwse architectuur in Holland

Het beeld van het gebruik van proportiestelsels is van oudsher vertroebeld door publikaties waarin het onderzoek op dit terrein tot loze rekenarij is gedegradeerd, merendeels voortgekomen uit een al te sterke veronderstelling dat het gebruik van ‘mooie maten’ en geometrie altijd met symboliek en diepere betekenissen beladen zou moeten zijn. Vooralsnog is het gebruik van meet- en rekenkundige systemen in eerste instantie te zien als een hulpmiddel bij het ontwerpen. Met eenvoudige verhoudingen en met behulp van passer en lineaal kon een architect zijn idee voor een gebouw tot een helder en sluitend ontwerp ordenen. De humanistische opvatting dat zuivere proporties een hogere, goddelijke ordening weerspiegelen, bleef hierbij de uitgangsgedachte, hoewel minder erudiete bouwlieden zich hier niet in alle gevallen als zodanig van bewust waren. Het gevoel voor de waarde van mooie maatverhoudingen, met ‘mateloosheid’ als tegengestelde, was in de 17de-eeuwse cultuur in Holland zo diep geworteld dat ook eenvoudiger ambachtslieden ‘in de maat’ konden werken zonder beladen te zijn met de filosofische oorsprong hiervan. Architecten als Vingboons en Post namen in deze een plaats in tussen de eenvoudige ambachtslieden en de intellectuelen van hun tijd die ook in de theoretische achtergronden waren geschoold, zoals Constantijn Huygens.

Conform bovenvermeld advies van Salomon de Bray uit 1631 kan men de classi-

[p. 20]

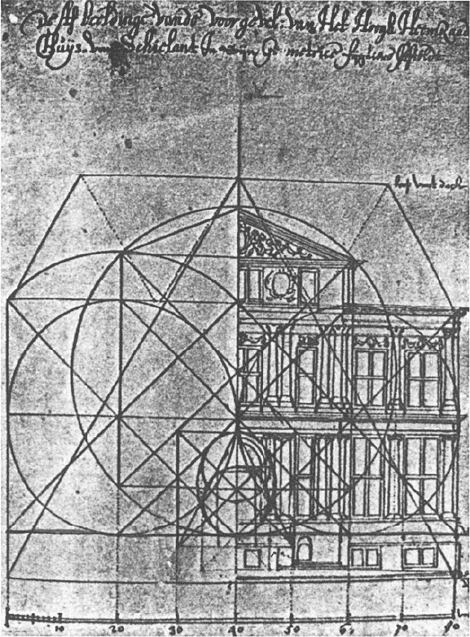
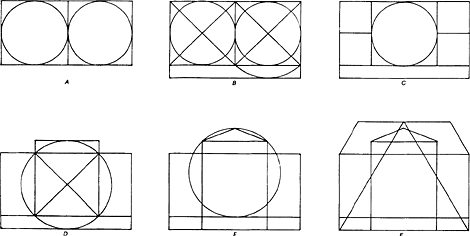
cistische ontwerpmethoden achterhalen door de ontwerpen nauwkeurig na te meten. Het spreekt vanzelf dat men hierbij alleen gebruik kan maken van ontwerptekeningen van de architecten zelf of betrouwbare prenten hiervan.^17. Wanneer men aldus op zoek gaat naar 17de-eeuwse ontwerpmethoden is het van belang te beseffen dat mooie mathematische figuren voor een 17de-eeuwse architect geen doel op zich zijn. Een mathematisch schema moet bovenal zinvol zijn bij het bepalen van de definitieve afmetingen van een gebouw. De belangrijkste punten en lijnen in het mathematische schema zijn gebruikt als ‘hoekstenen’ in het ontwerp. Omgekeerd moet een achteraf gerecontrueerd ontwerpsysteem derhalve een sleutel bieden voor de ordening van het hele gebouw. Cruciale punten van het systeem moeten dan samenvallen met de hoofdlijnen van het ontwerp. Alleen zo kunnen zin en onzin van gereconstrueerde proportieschema's worden onderscheiden.

De beste bron voor de reconstructie van een 17de-eeuws ontwerpproces, zijn de aanwijzingen van de architecten zelf. Nu zijn de beschikbare gegevens hierover zeer beperkt in aantal maar deze zijn bijzonder leerzaam. Het ontwerp van Jacob Lois voor het Schielandhuis in Rotterdam uit 1662 is naar het schijnt het enige project waarvan het proportieschema bewaard is (afb. 1).^18. Het uitgangspunt zijn twee tegen elkaar geplaatste vierkanten (afb. 2-A). Door de halve diagonaal van een van deze vierkanten met de passer naar beneden uit te slaan en zo het vierkant gedeeltelijk te omcirkelen, vindt men de hoogte van de basis (B). Vervolgens plaatst men één van beide vierkanten in het midden en bepaalt zo de middenrisaliet (C), omcirkelt deze nogmaals en vindt zo de hoogte van de attiek boven de middenrisaliet (D). Men schuift de cirkel met het ingeschreven vierkant omhoog om zo de totale hoogte van de middenpartij inclusief het fronton te bepalen (E). De hoogte van de nok van het dak wordt bepaald door vanuit de grondlijn een gelijkzijdige driehoek te construeren (F).

De grote hoofdvorm wordt dus bepaald door vierkanten en vervolgens wordt met behulp van omcirkelingen de definitieve omvang bepaald. Het gebruik van de gelijkzijdige driehoek om de hoogte van het dak te bepalen, blijft een uitzondering. Meestal zal het ontwerpschema zich beperken tot het stenen gedeelte van het gebouw en wordt het dak daarboven volgens eigen, praktische regels geconstrueerd, zonder direct verband met het maatsysteem daaronder. Het belangrijkste blijkt in eerste instantie de bepaling van de grote vorm van het gebouw, de maten van het muurwerk. De detaillering hiervan, zoals het plaatsen van de vensters en eventueel het aanbrengen van de klassieke orden, is zodoende een invulling van de vastgestelde grote vorm. Een proportieschema is in deze architectuur geen optelsom van kleine detailmaten maar een verdeling van de hoofdmaten in kleinere onderdelen.^19.

17. Men moet het ontwerp tot in de kleinste details kunnen na meten. Het is derhalve geheel uit den boze hiervoor onnauwkeurige opmetingen, pittoreske schetsen of foto's te gebruiken vanwege de grove vertekeningen van dit materiaal.

18. Deze tekening maakt deel uit van een serie van drie tekeningen in het handschrift oude en ware beschrijving van Schieland door Jacob Lois uit 1672 (Gemeentearchief Rotterdam). Zie voor de analyse van Terwen van het ontwerpsysteem van de gevel: R. Meischke e.a. (red.). Het Trippenhuis te Amsterdam. Amsterdam 1983, pp. 172-173.

19. Ook twee andere belangrijke voorbeelden, waarvan het ontwerpsysteem achterhaald is door de bestudering van de gravuren van de plattegronden en gevels, illustreren deze werkwijze, te weten het stadhuis van Amsterdam van Jacob van Campen en het Trippenhuis van Justus Vingboons. Zie resp. C. Wegener Sleeswijk. ‘De maten van het paleis op den Dam te Amsterdam.’ In: Bouwkundig Weekblad Architectura 1940, pp. 338-341 en R. Meischke, J.J. Terwen. ‘De architectuur van het Trippenhuis.’ In: R. Meischke (red.). Het Trippenhuis te Amsterdam. Amsterdam 1983, pp. 174-181.

Abstracte schoonheid en kubische eenvoud

Het streven van de classicistische architecten bleef niet beperkt tot het ordonneren van evenwichtige gevels. Het ideaal was een eenvoudig, alomvattend maatsysteem waaraan de ordening van zowel de gevels als de plattegrond zijn onderworpen. De gevelindeling weerspiegelt hiermee direct de verhouding van de ruimten erachter. In de ideale situatie is het proportiestelsel immers een ruimtelijk, driedimensionaal systeem, samengesteld uit een aantal grote kubussen. In de 17de-eeuwse

[p. 21]

bouwpraktijk kwam een dergelijke situatie vrijwel niet voor. Bij de bouw van buitenhuizen hadden praktische eisen van wooncomfort en financiën voorrang boven een theoretisch ideaal en in de steden waren de bouwpercelen meestal van dien aard dat de zuivere ordening slechts tot de gevel beperkt moest blijven.

Om nu eindelijk eens zijn ideeën over de ideale architectuur te etaleren, zonder

[p. 22]

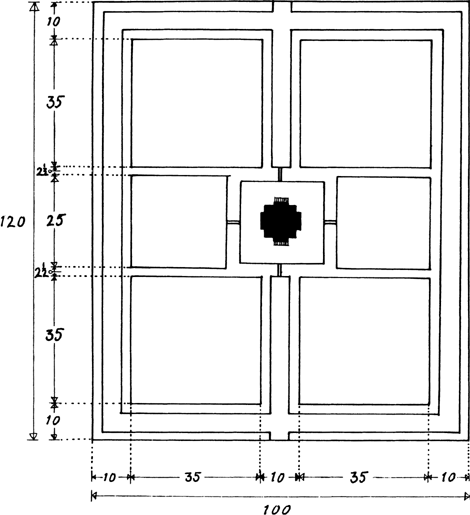
concessies ten opzichte van het beschikbare bouwterrein, financiën van de opdrachtgever of praktisch gebruik, publiceerde Philips Vingboons achter in zijn Afbeelsels der voornaemste Gebouwen (1648) het ontwerp van een ideale villa met bijhorende tuinaanleg (afb. 3).^20. Deze villa is een massief vierkant bouwblok dat midden op een vierkant eiland ligt. Op de hoeken van dit eiland zijn vierkante dienstgebouwen ontworpen in de trant van Huygens' Hofwijk. Het huis zelf heeft vier vrijwel identieke gevels die geheel in baksteen zijn opgetrokken met aan iedere zijde een middenrisaliet. Deze villa en het terrein eromheen zijn een schoolvoorbeeld van de toepassing van eenvoudige maatverhoudingen. Het hele gebied meet 100×120 Amsterdamse roede (afb. 4).^21. Dit terrein is verdeeld in vier eilanden van 35×35 roede (de boomgaarden), twee van 25×25 roede (de siertuinen) en een centraal eiland van 20×20 roede. De eilanden worden gescheiden door 2½ roede brede vaarten en 5 roede brede dijken. Een dijkweg over de lengte-as leidt naar het centrale eiland en in het midden hiervan staat de villa.

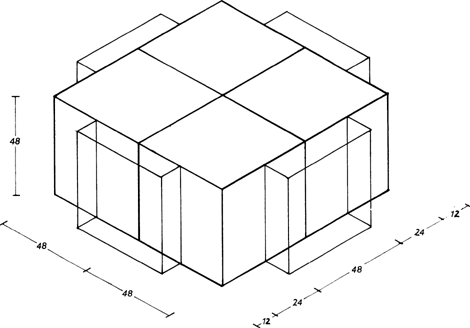
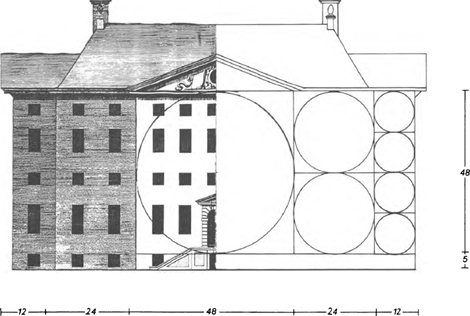
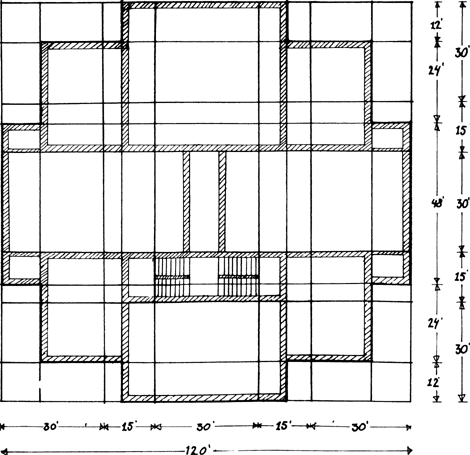
De totale maten van de villa zijn 120×120 voet met een hoogte van 53 voet vanaf het maaiveld tot aan de dakgoot. Men kan zich voorstellen dat Vingboons als volgt tot deze ordening is gekomen: het uitgangspunt zijn vier kubussen elk met een zijde van 48 voet, die aaneengevoegd zijn tot een blok van 96×96×48 voet (afb. 5). Aan elk van de vier zijden van dit grote blok wordt een 48 voet brede middenrisaliet geplaatst die 12 voet vooruit steekt. De totale omvang van de plattegrond komt zo op 120×120 voet. Dit geheel wordt op een souterrain geplaatst dat 5 voet boven het maaiveld uitsteekt. Het resultaat hiervan is een kruisvormig gebouw met aan elke zijde een gevelverdeling van 12, 24, 48, 24, 12 voet, oftewel in tien eenheden van 12 voet in een verhouding van 1:2:4:2:1 (afb. 6).

Deze zelfde maatverhoudingen van de gevels zijn ook het uitgangspunt geweest voor de ordening van de plattegrond. Hierbij is tegelijk met de verdeling van de breedte van 120 voet in tien eenheden van 12 voet een tweede verdeling van 120 in acht eenheden van 15 voet verweven (afb. 7). Dit dubbele maatsysteem levert vanzelf allerhande mooie verhoudingen in de verdeling van de ruimte in het ge-

20. Op fols. 53a, 53, 54, en 55 van zijn Afbeelsels uit 1648 geeft hij de plattegrond van het terrein en een plattegrond, een gevelopstand en een doorsnede van het huis.

21. Een Amsterdamse voet is 28,6 cm (11 duim). Een Amsterdamse roede bevat 13 Amsterdamse voeten en meet 371 cm. Een Rijnlandse voet is 31,4 cm (12 duim) en een Rijnlandse roede bevat 12 Rijnlandse voeten, 376 cm.

[p. 23]

[p. 24]

bouw, waarbij ook de maten van beide verdelingen met elkaar gecombineerd kunnen worden. Naast verhoudingen als 12×12 en 15×15 kan men zo kiezen uit een schier onbegrensde reeks mogelijkheden zoals 12×15 (= 4:5), 15×24 (= 5:8), 24×30 (= 4:5) en 30×48 (= 5:8) voor de grotere kamers en bijvoorbeeld 9×12 (= 3:4) en 15×9 (= 5:3) voor de kleinere vertrekken. Alle muren zijn langs de lijnen van dit ontwerpschema gelegd. Daar echter bij dit model geen rekening is gehouden met de dikte van de muren zelf, kunnen de werkelijke afmetingen van de vertrekken de mooie verhoudingen slechts benaderen zonder ze exact te bereiken.

Zo ligt er een helder, eenvoudig en ruimtelijk doordacht maatstelsel aan dit ontwerp ten grondslag waarbij alle ornamentiek verder achterwege gelaten is. Dit is

[p. 25]

[p. 26]

meer dan alleen mooi tekentafelwerk. Het is een driedimensionaal harmoniemodel dat de essentie van het classicisme illustreert, namelijk dat de schoonheid van de architectuur bepaald wordt door de zuivere proporties en dat de ornamenten slechts een toegevoegde schoonheid zijn.

Passen en meten in de praktijk

Hoewel de schaal en consequente doorvoering van het maatsysteem van Vingboons' ideale villa de realiteit van de 17de-eeuwse bouwpraktijk overstegen, vindt men in verschillende bestaande gebouwen uit die tijd dezelfde principes terug. In monumentale, vrijstaande gebouwen zal dat van zelfsprekend meer het geval zijn dan bij stadswoonhuizen, waarbij de architect de harmonische maatvoering meestal tot de voorgevel moest beperken.

De gravure uit 1664 van Pieter Post van het stadhuis van Maastricht (naar diens

[p. 27]

[p. 28]

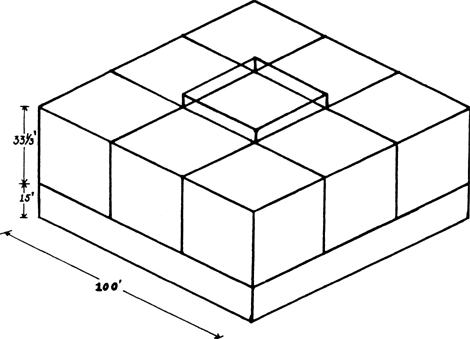ontwerp van 1656) toont hoe het ideaal van een vrijstaand monumentaal gebouw op een vierkante plattegrond van 100×100 Rijnlandse voet kon worden gerealiseerd, waarbij zowel plattegrond als gevelgeleding in één driedimensionaal maatsysteem zijn geordend (afb. 8).^22. De beganegrond is 15 voet hoog en de hoogte van de beletage en de bovenverdieping is samen 33⅓ voet. Het bouwblok van 100×100 voet lijkt zodoende samengesteld uit negen kubussen met een zijde van 33⅓ voet op een 15 voet hoog podium (afb. 9). De middelste van deze kubussen is de onderbouw van de toren. Naast de verdeling van 100 voet in 3×33⅓ komt aan de voorgevel en in de plattegrond ook een verdeling voor van 25 + 50 + 25 voet (afb. 10). De grote hal in het stadhuis (het Plein genaamd) is 50 voet breed, geflankeerd door 25 voet brede bestuursvertrekken (ook in dit geval zijn de muren langs de proportielijnen gelegd en zijn de uiteindelijke afmetingen van de vertrekken vanwege de reële dikte van de muren niet gelijk aan die van het schema). In de 50 voet brede hal staan vier zware pijlers die de onderbouw vormen van de toren met een breedte van 33⅓ voet. De voorgevel weerspiegelt de interne ruimteverdeling. De gevel heeft een brede middenrisaliet van 50 voet, corresponderend met de dubbele trap en het plein binnen. Deze risaliet wordt geflankeerd door wandvlakken van 25 voet, corresponderend met de bestuursvertrekken. Op de brede middenrisaliet van 50 voet (met vijf traveeën) springt een smallere middenpartij van drie traveeën vooruit die 33⅓ voet breed is, gelijk aan de breedte van de onderbouw van de toren midden in het gebouw. Beide systemen samen geven de gevel de volgende indeling: 25 + 8⅓ + 33⅓ + 8⅓ + 25 voet, hetgeen een verhouding inhoudt van 3:1:4:1:3.

22. In 1664 publiceerde Post Het Stadhuys van Maastricht, een serie met negen gravuren van Jan Mathijs, vier plattegronden, drie gevels en twee doorsneden. Later zijn deze prenten opgenomen in Les Ouvrages de Pierre Post. P. van der Aa, Leiden 1715. Zie voor het ontwerp van Post: K.A. Ottenheym. ‘Het stadhuis te Maastricht van Pieter Post.’ In: S.E. Minis e.a. (red.). Een seer Magnifick Stadthuys, Delft 1985, pp. 35-58.

[p. 29]

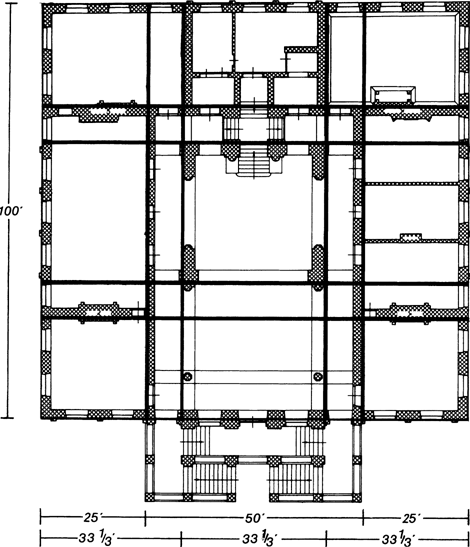
Figuur 10: plattegrond van het stadhuis van Maastricht met het schema van de verdeling in eenheden van 33⅓×33⅓ en van 25×25 voet (tekening auteur).

Kasteel Amerongen (1674), het Loo (1685) en kasteel Middachten (1695) zijn de bekende latere voorbeelden van het ontwerpen in kubische eenvoud. Dit ruimtelijke model is in de 17de eeuw in Holland verder zelden werkelijk zo consequent toegepast. Bij het ontwerpen van vrijstaande landhuizen, waarbij dit toch op zich mogelijk geweest zou zijn, liet men zich toch eerder leiden door wensen aangaande het wooncomfort. In een rechthoekig bouwblok zijn immers de vertrekken eenvoudiger van vensters te voorzien zonder verspilling van ruimte. Ook wanneer het ontwerp echter niet echt uit kubussen is samengesteld, blijft men voor de gevels met vierkanten werken. Van een integrale samenhang tussen de plattegrond en de gevel is dan uiteraard geen sprake meer.

[p. 30]

Figuur 11: het buitenhuis ‘Vegtvliet’ bij Breukelen, gravure uit 1674 van B. Stopendaal naar het ontwerp van Ph. Vingboons.

[p. 31]

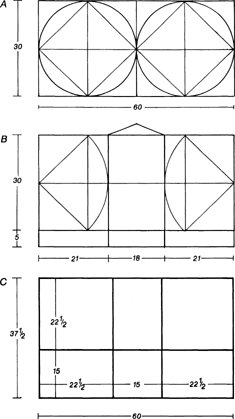
Figuur 12 (A, B): de proportionering van de voorgevel en (C) van de plattegrond (tekening auteur).

Zo ontwierp Philips Vingboons bijvoorbeeld circa 1665 het huis Vegtvliet bij Breukelen op een plattegrond van 60×38 voet en een hoogte van 35 voet (afb. 11).^23. De beganegrond ligt hier 5 voet boven het maaiveld. De voorgevel meet derhalve vanaf de beganegrond 60×30 voet en heeft een middenrisaliet van 18 voet breed, geflankeerd door zijvlakken met een breedte van 21 voet (21 + 18 + 21 = 60). Het ontwerp van de voorgevel is ontstaan met twee tegen elkaar geplaatste vierkanten van 30×30 voet (afb. 12-A). Een van deze wordt vervolgens in het midden geplaatst en geflankeerd door vlakken van 15 voet breed en 30 voet hoog, oftewel door twee opgestapelde vierkanten van 15×15 voet (B). Vervolgens worden de diagonalen van deze vierkanten van 15×15 voet met de passer naar binnen omcirkeld. Hiermee is de breedte van de gevelvlakken terzijde van de middenrisaliet bepaald, namelijk 21 voet (15√2 ≈ 15×7/5 = 21) en blijft er 18 voet over voor de middenrisaliet zelf (C). De verdeling 21 + 18 + 21 is hiermee vastgesteld en dit geheel is op een basis van 5 voet geplaatst.

23. Het ontwerp van de voorgevel en de plattegrond van dit huis zijn door Vingboons gepubliceerd als fols. 64 en 65 in diens Tweede deel van de Afbeeldsels. Amsterdam 1674.

[p. 32]

De zijgevel van het gebouw meet 38 voet en met een afwijking van een halve voet benadert de plattegrond de verhouding van 60:37½ = 8:5 (afb. 12-C). In de plattegrond is de verdeling van de voorgevel niet doorgezet. In plaats van de verdeling 21 + 18 + 21 vinden wij in de lengte een verdeling van 22½ + 15 + 22½ (= 3:2:3). In de verdeling van de breedte is een aansluitende verdeling van 15×23 (≈ 15×22½ = 2:3). Met een hoogte van 15 voet op de hoofdverdieping zijn de vertrekken op de beganegrond een evenwichtige ruimtelijke reeks, waarbij echter de dikte van de muren wederom afbreuk doen aan de theoretische volmaaktheid hiervan. Het voorhuis is in deze zin de enige ‘ongeschonden’ ruimte: lengte, breedte en hoogte zijn hier als een kubus van 15×15×15 voet. In de kamer aan de rechterzijde is dit theoretisch 22½×15×15 (= 3:2:2), in realiteit echter 20×14×15 voet. De maten van de grote zaal aan de linkerzijde zouden uitkomen op 37½×22½×15 (= 5:3:2) maar zijn uiteindelijk in het ontwerp tot 36×20½×15 voet gereduceerd.

Het realiseren van een abstract matenstelsel bleef bij het ontwerpen van stadswoonhuizen ondergeschikt aan het belang van een bruikbare indeling van de beschikbare ruimte. Het werken met afgewogen maatverhoudingen beperkte zich bij de stadshuizen derhalve meestal tot de voorgevels. Alleen bij de grote huizen, zoals bijvoorbeeld in het tweede deel van de Amsterdamse grachtengordel, is enige samenhang in het ontwerp van de gevels en de bijhorende plattegronden te bespeuren. Voor de uiteenlopende typen van woonhuisgevels bestonden verschillende min of meer standaard maatverhoudingen. In het werk van Vingboons bijvoorbeeld, dat ons door diens eigen publicaties goed bekend is, blijken bij de verschillende standaard breedte-maten in Amsterdam vaste standaard hoogte-maten gebruikt te zijn.^24. Hierbij doet het er niet toe of een gevel ornamentloos is, met pilasters is bekleed of met barokke ornamenten gedecoreerd is. Ook achter de meer vrije en luchtigere varianten in de vormgeving van de gevels steekt een hecht en helder proportiesysteem. Hieronder volgt een selectie uit de verschillende ontwerpsystemen die Vingboons voor huizen van verschillende breedte heeft toegepast (afb. 13):

De gevels met een breedte van 25 voet worden 50 voet hoog (= 1:2), gemeten vanaf de straat en exclusief de geveltop daarboven (afb. 13A). Gevels van 30 voet breed krijgen een basis van 5 voet hoog en zijn vanaf die basis 50 voet hoog (30:50 = 3:5). De top daarboven is 10 voet breed en 10 voet hoog, exclusief de bekroning (B). Gevels met een breedte van 40 voet krijgen een basis van 6 à 8 voet en zijn vanaf die basis 40 voet hoog tot aan de dakgoot, die bij deze gevels evenwijdig aan de straat is (40:40 = 1:1). De middenrisaliet kan variëren en is bijvoorbeeld 20 of 24 voet breed hetgeen resulteert in een gevelgeleding van 10 + 20 +10 of 8 + 24 + 8 voet (= 1:3:1) (C). Gevels van 50 voet breed hebben een basis van 10 of 12 voet. Vanaf deze basis is het huis tot aan het dak 36 voet hoog. De middenrisaliet is bijvoorbeeld 30 voet breed zodat de gevel is geleed in 10 + 30 + 10 voet. De hoogte van de verdiepingen meet tot aan het hoofdgestel 30 voet zodat de middenrisaliet gezien kan worden als een vierkant van 30×30 voet. Door de hele diagonaal hiervan met de passer naar beneden uit te slaan wordt de 12 voet hoogte van de basis geconstrueerd en door de halve diagonaal naar boven te omcirkelen vindt men de 6 voet hoogte van het hoofdgestel (D).

Op deze en andere basisschema's waren in uitwerking en decoratieve afwerking schier eindeloze variaties mogelijk. Hierbij kon gekozen worden uit een pilaster-

24. Hierbij zijn de ontwerpen onderzocht uit Ph. Vingboons. Afbeelsels der voornaemste Gebouwen. Amsterdam 1648 en Ph. Vingboons. Tweede deel van de Afbeeldsels der voornaemste Gebouwen. Amsterdam 1674 (zie noot 1 voor een gedetailleerde bespreking hiervan).

[p. 33]

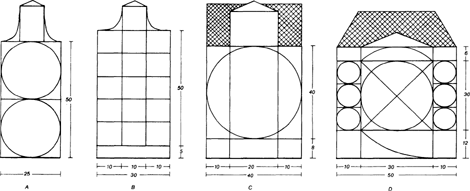stelling, vrije ornamenten, een natuursteenbekleding of een geheel sobere baksteengevel. Wanneer men er voor koos een gevel verder te versieren met een pilasterstelling, werd het mathematische ontwerpschema hiermee verder ingevuld. De maatvoering van de pilasterorden op zich is door de Italiaanse tractaatschrijvers aan strikte regels onderworpen. Het was evenwel niet altijd mogelijk om de voorgeschreven proportionering van de orden daadwerkelijk in het grote mathematische schema in te passen. Alleen bij de zeer brede gevels van 50 voet of meer, was er hiervoor voldoende ruimte. Bij de smallere gevels volgde men alleen in de detaillering van de kapitelen, basementen en lijsten precies de tractaten. De schachten van de pilasters werden echter ingekort of uitgerekt, al naar gelang nodig was om de pilasters in het basisontwerp in te passen.^25.

25. Zie voor een nauwkeurige behandeling van de toepassing van pilasterorden in de 17de eeuw in Holland: Meischke, Terwen 1983 (zie noot 19), pp. 175-181 en Ottenheym 1989 (zie noot 1), pp. 166-172.

Besluit

Voor zover bekend blijken architecten als Van Campen, Post en Vingboons een uitgewerkt systeem gebruikt te hebben waarmee op eenvoudige wijze alle soorten van gebouwen konden worden ontworpen. Toch is het geen star en academisch principe maar biedt het zoveel variatiemogelijkheden dat elk ontwerp uiteindelijk een eigen karakter heeft kunnen krijgen. Dit ontwerpsysteem vormt echter de kern van de esthetica van hun architectuur: de schoonheid van het classicisme ligt niet in het ornament maar in de harmonieuze proporties.