De Vlaamsche School. Jaargang 14

Drukking der vloeibare lichamen op die welke zich in hun midden bevinden.

Wanneer een lichaam in een vocht gansch ondergedompeld is, dan verliest dit lichaam een gedeelte van zijn gewicht, evenwaardig met het gewicht van den omvang van het vocht, welk door het lichaam verplaatst wordt. Inderdaad, veronderstellen wij dat een lichaam van eenen kubieken



vorm gansch onder water zij, alsdan hebben de drukkingen op deszelfs vier zijdswanden geen den minsten invloed op deszelfs zwaarte, maar zijne onderste vlakte ondergaat van onder naar boven eene drukking gelijk zijnde aan het gewicht van eene kolom water, die voor grondzuil heeft deze vlakte zelve, en voor rechtstaande hoogte den afstand b h; integendeel ondergaat de bovenste vlakte van dit lichaam eene drukking gelijk aan het gewicht der kolom a h. Deze twee laatste drukkingen zijn tegenovergesteld en ongelijk; de onderste is de grootste, en het verschil dat tusschen beiden bestaat, wordt vertegenwoordigd door eene kolom water, die voor grondzuil heeft de onderste vlakte van het kubiek lichaam, en voor rechtstaande hoogte de lijn b a. Diensvolgens wordt dit verschil ver-

[p. 118]

tegenwoordigd door den omvang zelf van het kubiek lichaam; ook wordt dit opgelicht door eene drukkingskracht gelijk aan het gewicht van eenen gelijken omvang water, Men begrijpt licht dat deze beredeneering altoos toepasselijk is, hoedanig ook de vorm van het ingedompeld lichaam zij. Uit dit voorgaande blijkt:

a. Een lichaam, welks betrekkelijk gewicht grooter is dan dit van het vocht waarin het gedompeld ligt, gaat naar onder, behoudende alleen de overmaat van zijn gewicht boven dit van het verplaatste vocht; ook ziet men dat zware voorwerpen, zooals steenen, veel gemakkelijker ondersteund worden onder water, dan wel er buiten.

b. Een lichaam, welks betrekkelijk gewicht min groot is dan dit van het vocht, waarin het zich bevindt, klimt tot deszelfs oppervlakte krachtens de overmaat van 't gewicht van het verplaatste vocht op zijn eigen gewicht, en wanneer het tot deze vlakte gekomen is, dan vlot het, verplaatsende eenen omvang water welks onafhankelijk gewicht gelijk is aan het zijne. Als voorbeelden zullen wij hier aanhalen, dat hout, kurk, enz. op water vlotten, dat een stuk ijzer op kwik vlot, en dat men meermaals, om zware voorwerpen uit het water te halen, aan deze er anderen hecht, wier betrekkelijk gewicht minder is dan dit van het water, en die derhalve neiging hebben om tot deszelfs bovenvlakte te klimmen.

c. Een lichaam waarvan het betrekkelijk gewicht gelijk is aan dit van het vocht waarin het geplaatst is, blijft in evenwicht in verschillige standplaatsen van het vocht, alsof het aan de zwaartekracht niet meer onderworpen ware. Deze gelijkheid van betrekkelijk gewicht bestaat zelden in de natuur, doch ze kan tot stand gebracht worden. Met eenige voorzorgen, bij voorbeeld, is het mogelijk een ei in evenwicht te houden in water waarin eene genoegzame hoeveelheid zout is opgelost.

De grondregel volgens welken een lichaam in een vocht gedompeld, een gedeelte van zijn gewicht verliest gelijk aan dit van den omvang vochts, welk verplaatst wordt, staat bij de natuurkundigen, onder den naam van grondstelsel van Archimedes bekend.

Deze grondregel kan nog onmiddellijk bewezen worden door proefnemingen met de vochtwegerschaal.



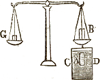
A is een kleine koperen cylinder aan een paardshaar hangende. Deze cylinder is juist zoo groot dat hij de binnenruimte van den hollen cylinder B, teenemaal kan bekleeden. Men evenaart het gewicht dezer beide lichamen door gewichten G die men in de andere schaal legt, daarna vult men het vat C D met water tot dat de cylinder A gansch onder zij; alsdan ziet men de gewichten G overhangen, en om het evenwicht te herstellen is het voldoende den cylinder B met water te vullen. Daaruit kan men besluiten dat de cylinder A in water gewogen eene hoeveelheid van zijn gewicht verloren heeft die juist gelijk is aan het gewicht van het door hem verplaatst water. Uit deze proefneming kan men echter nog besluiten dat, voor eene gelijke hoeveelheid stof, de in vocht gedompelde lichamen eene grootere hoeveelheid gewicht verliezen, naarmate hun omvang en het betrekkelijk gewicht van het vocht grooter zijn; ook valt het niet lastig te begrijpen hoe het mogelijk is met ijzer, welks betrekkelijk gewicht grooter is dan dit van het water, schepen te bouwen, die, even als houten, op het water vlotten, en waarom de waterdracht der schepen grooter is in zoet- dan in zeewater, het betrekkelijk gewicht van dit laatste grooter zijnde door de er in opgeloste zoutstoffen.

D^r F.-J. Matthyssens