Over de hellende vlakte.
Het is blijkbaar dat een lichaam, op eene vlakte geplaatst, niet in evenwicht kan wezen, tenzij de uitkomst der krachten die het tot beweging aandrijven, door het punt van aanraking ga, en rechtstandig zij op de richting der vlakte. Dit grondstelsel is toepasselijk op de hellende vlakte.
A C is eene hellende vlakte die met de liggende lijn A B
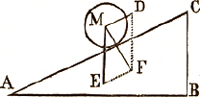
eenen driehoek C A B uitmaakt. Op de hellende vlakte is geplaatst een lichaam M dat door de zwaartekracht M E tot beweging wordt aangedreven, en wederhouden wordt door eene kracht M D evenwijdig met de vlakte. Welke is, in dit geval, de betrekking der macht M D tot de zwaartekracht M E? Om die te bepalen, behoeft men het medegedeeld vierkant figuur der krachten die eenen hoek uitmaken, te vormen.
Daartoe zullen wij veronderstellen dat M F de lengte en de richting der uitkomst zij, welke richting, tot evenwicht, rechtstandig zijn moet op A C; maken wij nu het vierkant M E F D, en dan zullen wij bemerken dat de krachten M D en M E wederzijds vertegenwoordigd zijn door hunne lijnen of door de lijnen E F en D F. Men ziet ook dat de driehoek M D F gelijkvormig is met den driehoek B A C. Diensvolgens is de betrekking der macht M D tot de macht M E gelijk aan die der hoogte C B der hellende vlakte tot derzelver lengte C A: wanneer C B 4 voet lang is, en C A 8 voet, dan zal eene macht M D, gelijk aan 4, eenen last gelijk aan 8 kunnen evenaren.
Ingeval de macht M D, in
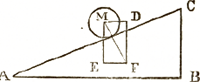
plaats van evenwijdig te zijn met A C, evenwijdig is met A B, dan vindt men door het opstellen van het vierkantig figuur der krachten, dat de betrekking der macht M D tot de kracht M E, gelijk is aan die van B C tot B A.
Uit het voorgaande blijkt dat, wanneer de lengte der hellende vlakte, even als het gewicht van het lichaam M, dezelfde blijven, de macht M D, voor het evenwicht, zooveel minder zal moeten zijn, als de hoogte der helling minder lang is.
Men gebruikt dagelijks de hellende vlakte om zware lasten op wagens of schepen te laden.
Dr F.-J. Matthyssens.